基于局部扩展的社区发现研究现状

史艳翠，王嫄，赵青，张贤坤

（天津科技大学计算机科学与信息工程学院，天津 300457）

1 引言

社区的定义为网络中所有节点集合的一个子集，该子集内节点之间的连接相对于与子集外其他节点之间更紧密[1]。社区发现则是在一个图或者社会网络中找出相关节点集合的过程，这项工作在一些文献中也称为图聚集或局部图划分等[2-3]。社区发现可以为用户需求获取、舆情监测等研究提供理论依据，具有重要学术研究意义和实用价值。

社区发现方法可分为全局优化和局部优化这两类。与全局优化相比，局部优化不需要整个网络的信息，主要基于局部网络结构信息发现局部或整个网络的社区。因此，局部优化更适用于大规模社交网络的社区发现。李建华等[1]根据不同的局部优化策略，将现有的局部优化社区发现方法大致分为局部扩展优化、派系过滤、标签传播以及局部边聚类优化四类。其中，基于局部扩展优化的社区发现方法的思想是根据定义的局部度量，从给定的初始节点逐步合并近邻节点，从而进行局部扩展优化，该方法包括2个步骤：种子的选择和将种子扩展为社区[4]。该方法能有效地揭示局部社区结构、提取有意义的局部聚类信息，并且为在线社区挖掘提供了一个非常有效的途径。本文通过跟踪研究，总结现阶段该领域的研究成果及存在的问题，并对需要进一步探索或研究的问题进行展望。

2 种子的选择方法

种子的选择对基于局部扩展的社区发现方法非常重要。种子既可以是边也可以是节点，既可以是一组互不连接的独立节点，也可以是紧密连接的子图/结构/核。常见的种子选择方法包括随机选择某个不属于任何社区的节点或边、根据全局排名、根据局部排名、选择构成规模不小于k的极大团、选择k-回路、使用混合方法等方法选择种子。

2.1 随机选择某个不属于任何社区的节点或边

Lancichinetti等[5]在提出的局部适应度算法（LFM, local fitness method）中，随机选择某个不属于任何社区的节点作为种子；Huang等[6]在提出的局部紧密度扩展算法（LTE, local tightness expansion）中也采用了同样的方法选择种子。Baumes等[7]在提出的迭代扫描（IS, iterative scan）社区发现方法中使用随机选择的边作为种子。

随机选择方法的缺点是既没有考虑节点的权重值又没有考虑网络的拓扑结构信息，且由于其随机性使社区发现的结果与种子质量选择的好坏有关。但由于该方法简单、时间复杂度小，因此仍然有很多研究人员使用该方法选择种子[8-10]。

2.2 根据全局排名选择种子

根据全局排名选择种子的方法根据节点权重值在整个网络中的排名选择种子。

Baumes等[7]在提出的排名移除（RaRe, rank removal）社区发现方法中采用移除策略选择种子节点。依次移除网页排名最高或节点度最大的节点，直到剩下一些在给定规模内且连接较少的结构。这些结构被视为每个簇的核，即初始社区。该方法有如下缺点：1） 由于每次删除节点后，都需要对剩余节点重新计算网页排名或节点度，因此效率低；2） 该方法的假设不恰当，因为有时排名在前的节点更适合做种子节点。类似地，龙渊[11]也采用移除策略选择种子节点，与 RaRe所不同的是，该方法通过删除影响力最小的节点，找到具有最大影响力的节点作为初始种子集合。由于选择的初始种子集合中可能包含孤点，直接使用孤点作为种子可能导致发现的社区结果不理想，因此该方法根据给定的规则将孤点扩展为仿团集，将生成的仿团集作为种子。

为了提高种子选择的效率，Baumes等[12]提出了链接聚合方法（LA, link aggregate）。该方法首先按照一定准则（例如，递减的网页排名）对节点进行排序，然后按照顺序依次执行，如果节点添加后不能改善任何簇的密度，则把它选做种子，并生成一个新簇。与RaRe相比，由于LA只需要对节点排序一次，在选择种子节点时，效率得到了很大提高。

为了更准确地选择种子节点，国琳等[13]在提出的OClu-detect算法中计算节点的权重值时，考虑了节点与邻域节点的平均连接强度以及邻域节点间的关联密度的影响。该方法首先根据节点的权重按照降序对节点进行排序，然后选择节点序列中排名最前，且未标记或其邻居未全部标记的节点作为种子，并将选为种子的节点从节点序列中删除；重复上述操作，直到被发现的节点全覆盖或大部分覆盖整个网络。Yang等[14]选择权重最大的节点（WM，weight maximum）在计算节点权重值时考虑了边的权重，该方法首先根据节点的权重按照降序对节点进行排序，然后选择节点序列中排名最前，且未出现在已发现社区中的节点作为种子，直至种子候选集为空。

当网络规模比较大时，对节点进行排序的时间消耗比较大，因此，一些研究人员选用最大值来降低时间复杂度。例如，陈俊宇等[15]在提出的半监督局部扩展式重叠社区发现办法（SLEM，scmi-super-vised local expansion method）中利用网络节点的拓扑特征——度中心性选择种子。在这种方法中，节点的邻居数量即为节点的权重值，在未标记的节点中选择具有最大度中心性的节点作为种子，并为该节点的周围邻居设置相同的标签，然后在未标记的节点中重复上述操作。Whang等[16]提出的spread hubs方法与上述方法类似，选择节点度最大的未标记节点作为种子。杨贵等[17]在提出的基于加权稠密子图的重叠聚类算法（OCDW, overlap community detection on weighted networks）中选择种子节点时，考虑到选择的种子既要位于网络的拓扑中心位置且种子之间在网络结构中应相距较远，因此，使用节点的加权值作为节点的权重，并选择权重最大的节点作为种子，在选择下一个种子时，根据设定的规则降低已成为种子的节点被再次选择的概率。Cao等[18]在提出的交通社区发现算法（TRACED, transportation community detection）中选择权重高且大于阈值的边以及相应的节点作为种子。

全局排名选择方法有如下缺点：1） 选择的种子可能是hub节点，使用这些种子有可能导致得到的社区发现结果比较差；2） 使用该方法选择的种子的多样性无法保证。

2.3 根据局部排名选择种子

根据局部排名选择种子的方法根据节点权重值在局部网络中的排名选择种子。

一些研究人员根据节点的最近邻信息选择种子。例如，Chen等[19]选择具有局部最大度的节点（LMD, local maximum degree）作为种子；Deshpande等[20]使用链接预测（LP1, link prediction）方法选择种子时，选择具有局部最大相似度的节点作为种子；Hao等[2]选择具有局部最小传导性的节点作为种子；而Gleich等[21]则选择具有局部最小传导性的邻域社区（LMC, locally minimal conductance）作为种子；Wang等[22]在提出的局部社区中心算法（LCC,locating community centers）中选择具有局部最大结构中心度的节点作为结构中心，在计算结构中心度时考虑了节点的密度和节点间的相对距离；Su等[23]在提出的基于随机游走的算法（RWA, random walksbased algorithm）中使用紧密连接的子图作为初始社区，首先根据局部最大度选择K（K表示选择的种子节点或种子子图的数量）个初始节点，然后选出给定初始节点的局部最大度节点，则具有局部最大度的节点、给定初始节点以及它们的一个共同邻居构成3个节点的种子社区。

上述方法仅利用了节点的最近邻信息。为了更准确地选择种子，汪涛等[24]在提出的基于核心节点跳转的局部社区发现算法（LCD-NJ, local community detection based on the core nodes jumping）中首先计算给定节点k跳范围内所有邻近节点的中心度，然后选择中心度大于给定阈值的节点作为种子。常振超等[25]在提出的影响力节点集扩展的局部社团检测方法（IN-LCD, local community detection based on influential nodes）中选择给定节点的所有最近邻和次近邻为种子候选集，然后使用最近邻和次近邻信息计算节点的影响力，并根据节点的影响力对候选种子节点进行降序排序。但是这2种方法主要用于发现包含某个节点的局部社区。在全网社区发现中，可以借鉴上述方法，利用k跳范围内节点的信息选择种子节点或计算节点的权重值。

Whang等[16]在提出的graclus centers方法中，通过计算节点和所在簇的距离来确定节点的权重。该方法选择种子的过程如下。首先使用graclus执行从上到下的层次聚类得到大量的簇，然后计算节点到属于簇的质心的距离，并选择距离最小的节点作为种子。该方法可以得到多样性的节点，且计算复杂度不是太大。

局部排名选择方法的缺点是有可能无法发现最大的社区，而使用极大团作为初始节点的社区发现方法则可以解决该问题。

2.4 极大团

Lee等[26]在提出的贪婪团扩张算法（GCE,greedy clique expansion）中，选用规模不小于3或4的派系作为初始节点。Shang等[27]则选择规模不小于4的派系作为初始节点。李婕[28]采用基于派系过滤的算法选择种子节点，该方法为了使选择的种子群组具有层次性，从最大的派系直至最小的派系逐级过滤构造种子群组。

极大团选择方法的优点是可以解决社区发现结果的不稳定性问题，缺点是寻找派系所需的计算量非常大[29]，难点是派系最小规模的确定，即k的值。在设定k值时，存在2个问题：1） k值太大或太小都会导致社区发现的结果不理想；2） 相似的派系会导致完全相同的社区冗余[15]。另外，如果将所有发现的派系作为初始节点，社区发现的计算时间非常大。为了解决该问题，Becker等[30]根据网络中节点的数量来限制选择的派系的数量。这种种子选择方法不适合密度较小的网络。

2.5 k-回路

肖觅等[31]考虑到随机选择某个不属于任何社区的节点和极大团的缺点，使用k-回路作为初始节点，并根据小世界和六度分割理论，设定3≤k≤6。与极大团相比，k-回路放松了对边的密度的要求，适用于密度稀疏的网络。

2.6 混合方法

为了克服单种选择方法存在的缺点，混合方法通过综合2种或多种方法选择种子。Shang等[4]为了避免高的计算复杂度和全局排名方法的缺点，提出了一种新的选择边作为种子的方法，信息理论和期望值最大化（ITEM, information theory and expectation and maximization）。。该方法首先使用信誉、强度和特异性（RSS, reputation, strength, specificity）选择候选种子，其中，RSS是一种局部排名方法；然后使用最大化全局信息增益方法（MGIG, maximizing global information gain）选出最终的种子，MGIG从全局角度在候选集中选择信息分布最大的节点作为种子。

Wilder等[32]综合随机和局部排名这2种方法，提出了一种选择种子节点的方法，ARISEN。首先，随机选取T（T＞K）个节点，并使用R步的随机游走找出每个节点的一个小子图；然后，根据子图计算每个节点的权重向量，使用正比于权重向量的概率来选择种子节点。该方法的时间复杂度只与随机选取的T个节点和R有关，因此效率得到了提高。而Zhou等[33]综合随机和局部排名这 2种方法提出了基于最小集群的局部社区发现方法（NewLCD, local community detection algorithm based on the minimal cluster）。首先，随机选取K个初始节点；然后，按照以下方法找出包含每个初始节点的最小簇：在给定初始节点的邻居集合中，找出与给定初始节点有最多共同邻居的节点，该节点、给定初始节点和它们的共同邻居构成最小簇，即种子。

张忠正[34]考虑到选择单个节点作为社区的种子时会存在一些问题，因此，通过综合全局排名和局部排名选择核心区域作为种子。首先，根据节点的核心值对全部节点进行降序排序构成优先级列表；其次，选择优先级列表的第一个节点作为初始的种子节点；再次，从该种子节点的邻居节点中根据局部排名选择k-1个节点与其合并构成核心区域；最后，对核心区域进行扩展，如果形成社区，则将社区内的节点从优先级列表删除，否则，将选择的种子节点从优先级列表删除。重复上述操作，直至优先级列表为空。该方法可以有效地避免将桥接点被选择为种子节点。

表1列出了上述种子选择方法的时间复杂度。其中，NU=|U|和NE=|E|分别表示网络中节点和边的数量；p表示边的平均邻居数量；NnU表示社区或节点的邻域的节点平均个数；NnkU表示给定节点k跳内邻居节点的个数，k≥2；T表示候选种子节点/初始社区的数量；Nvc=|UC|和Nεc=|EC|分别表示双连通核中节点和边的数量，UC和EC分别表示双连通核中节点和边的集合，且Nvc≤NU，Nεc≤NE[16]；t表示每次删除的节点的个数，1≤t≤（max-min），min和max分别为种子节点的数量的下限和上限值[7]；kC表示规定的核心区域的规模[34]。

由表1和上述分析可得以下结论。

1） 时间复杂度。随机选择方法的时间复杂度最小。混合选择方法综合了多种方法的优点，大多数情况下时间复杂度不是太大。全局排名方法需要计算所有节点的权重值，有时还需要计算多次，由于计算复杂度与节点的规模呈正比，当应用在大规模的网络（例如有上亿用户的微信）时，其计算复杂度会很大。基于局部排名的方法在选择节点时，只需要与局部节点进行对比，在最好的情况下，其时间复杂度可以降为NnUK。k-回路的时间复杂度与节点和边的数量成正比，所以在大规模网络中，其时间复杂度比较大。极大团的时间复杂度最大。

表1 种子选择方法的时间复杂度的对比

2） 种子的质量。由于其随机性，使用随机选择方法选取的种子节点的质量无法保证。全局排名方法可以选择出网络中最有影响力的节点，但这些节点有可能不适合作为种子节点，例如当网络中最有影响力的节点分布比较集中时，则导致选择的种子比较集中，从而使社区发现的质量比较差。基于局部排名的方法多样性比较好，选择的种子节点在网络中分布比较均匀。极大团和k-回路种选择方法与网络的拓扑结构有关，当网络中疏密度不均匀时，会出现与全局排名类似的问题，选择的种子多样性比较差。混合方法由于综合了多种选择方法的优点，一般情况下，选择的种子节点的质量比较好。

3） 适用网络。综合时间复杂度和种子的质量，总结出各种种子选择方法的适用网络如下。随机选择方法对网络没有要求，可以应用在任何网络中。全局排名方法由于其时间复杂度与节点规模呈正比，因此适用于小规模、且权重值较大的节点分布比较均匀的网络，但对稀疏性没有要求。局部排名方法可以应用在任何网络中。k-回路和极大团则适用于密度比较大且k-回路和极大团分布比较均匀的小规模的网络中。混合方法则根据综合的方法确定其适用网络。

3 局部扩展优化方法

本文将局部扩展优化算法分为基于无监督的局部扩展优化方法和基于半监督的局部扩展优化方法两大类进行介绍。

3.1 基于无监督的局部扩展优化方法

当网络中无法获取节点所属社区的任何标记信息时，可以使用无监督的局部扩展优化方法。最简单的扩展方法就是直接添加种子的全部邻域节点到相应的社区[13]，但该方法发现的社区的准确性不高。贪婪扩展是最常用的一种社区扩展方法，它通过最大化或最小化某个给定的函数或者社区的某个特征指标来扩展局部社区，本文给出了常用的几种贪婪扩展方法。

1） 最大化适应度函数

在 Lancichinetti等[5]提出的 LFM 社区发现方法、Lee等[26]提出的GCE社区发现方法中，通过贪婪地最大化局部适应度函数来实现局部扩展优化。LFM的扩展过程如下：① 计算每个种子边界节点的适应度，如果计算得到的适应度的最大值为正值，则将该边界节点添加到相应的社区中；② 计算该社区内每个节点的适应度；③ 如果某节点的适应度为负值，则将该节点从社区中移除；④ 如果发生③，则执行②，否则执行①。张忠正[34]采用了与LFM相同的局部扩展方法，与LFM的区别是，在扩展过程中，如果选择的种子节点被删除，则停止扩展。

与LFM不同，在GCE中，只需要计算边界节点的适应度，如果计算得到的适应度的最大值为正值，则将该边界节点添加到相应的社区中；否则，终止操作[26]。杨贵等[17]提出的 OCDW（overlap community detection on weighted networks）基于加权稠密子图的重叠聚类算法、汪涛等[24]提出的LCD-NJ（local community detection based on the core nodes jumping）基于核心节点跳转的局部社区发现算法以及常振超等[25]提出的IN-LCD（local community detection based on influential nodes）影响力节点集扩展的局部社团检测方法采用与 GCE类似的方法实现局部扩展，但这些方法没有限定扩展的候选节点是邻域节点。为了减少局部扩展的时间，龙渊[11]对 GCE算法中的局部扩展方法进行了改进，对适应度为负值的节点进行了分析，将不可能加入社区的节点在后续的扩展中删除。

上述局部扩展方法根据适用的场合不同，适应度函数的定义有所不同。LFM和GCE根据社区的内部度数和外部度数定义适应度函数；IN-LCD和LCD-NJ则根据社区的相似度和社区的适应度来定义节点的适应度函数。上述这些方法只适用于无权网络。为了适用于加权网络，OCDW方法在定义社区的适应度函数时，考虑了边的权重值，并用适应度函数评价社区的稠密程度。李婕等[28]使用加权网络中基于局部适应度方法的派系过滤（CLFMw,clique percolation based local fitness method for weighted network）构建群组，则在定义适应度函数时考虑了节点的度数和边的权重，只有当适应度函数的值大于给定的增量阈值时，才将节点加入到相应的社区。

2） 最大化可调密度增益

Huang等人在提出的LTE算法中通过最大化可调密度增益实现局部社区扩展[6]。其扩展过程包括两步：① 更新过程，更新社区的邻居集合，并计算邻居集合中每个节点与社区的相似度；② 添加过程，选择与社区相似度最大的节点，如果该节点的可调密度增益大于零，则将该节点添加到社区，否则将该节点从邻居集合移除，并按照结构相似度的降序依次分析其余节点。重复上述过程，直到所有节点加入到相应的社区。

3） 最大化局部相关度

肖觅等[31]提出的回路融合社区发现算法（CM,circuits merging）中通过贪婪地最大化局部相关度来实现局部扩展优化。具体过程如下。① 如果节点（不属于任何种子）只和一个社区（初始时由种子构成的社区）连接，则将其添加到该社区。② 如果节点与多个社区相连，则计算该节点与每个社区的相关度。③ 如果计算得到的相关度的最大值只有一个，则将其添加到相应的社区；如果计算得到的相关度的最大值有多个，则将节点添加到相应的多个社区。重复上述步骤，直到所有节点都被添加到相应社区。

4） 最大化模块度

在Shang等[27]提出的重叠社区发现方法中，通过最大化模块度实现贪婪扩展。如果节点只有一个社区相连，则直接将节点添加到该社区。与CM算法不同，当节点与多个社区相连时，通过临时添加和最终添加来实现扩展，具体如下：① 临时添加，计算该节点与每个社区的连接度，如果连接度大于给定的阈值，则将该节点添加到相应的社区，否则，将该节点添加到连接度最大的社区；② 最终添加，遵循模块度最大化原则，将节点添加到相应社区。Zhou等[33]在提出的 NewLCD方法中同样采用了最大化模块度的方法实现局部社区扩展，首先计算初始社区的邻域节点和相应的模块度，然后将邻域节点中具有最大模块度的节点添加到初级社区，重复上述操作，直至没有节点能添加到初级社区。Chen等[19]在提出的局部社区发现算法（LCDA,local community detection algorithm）中选择与种子有最多共同邻居且能最大化模块度的邻域节点进行扩展。Yang等[14]在提出的局部扩展方法中，首先通过计算近似的网页排名向量来确定支持集，然后根据模块度最大化和传导率最小原则（HMSC, high modularity and small conductance）选择支持集中的节点进行局部扩展。

5） 最大化子图或簇的密度

Baumes等[12]在提出的LA方法中，通过最大化簇的密度实现局部扩展，将节点添加到能增加社区的密度的社区。Wang等[22]在提出的局部社区扩展算法（LCE, local community expansion）中通过最大化子图密度实现局部社区扩展。过程如下：以选择的结构中心作为初始的社区，将能增加社区密度的邻域节点添加到该社区，删除社区中具有负增益的节点，重复上述操作直到社区的密度不能改善。

6） 最大化概率

Su等[23]在提出的RWA方法中使用随机游走策略实现局部社区的扩展。该扩展方法首先基于随机游走计算未标记节点属于各个初步社区的概率，然后根据计算得到的概率，将该节点添加到最有可能属于的社区。重复上述操作，直到所有节点添加到相应社区。

7） 最大化中心度

Nathan等[8]使用个性化的中心度——网页排序或 Katz中心度（PPKC, personalized PageRank or Katz centrality）进行局部扩展。首先计算给定种子节点的个性化的中心度，然后根据给定局部社区的规模，例如社区大小为NCU，则选择中心度最大的NCU个节点构成局部社区。

8） 最小化传导值

传导值是度量社区质量常用的一种评价指标，传导值越低，社区质量越好[10]。Whang等[16]提出了一种基于个性化网页排名的种子扩展方法，该方法通过贪婪地最小化传导值实现种子扩展。具体步骤为：1） 以给定的某个种子节点及其邻居作为初始节点；2） 计算个性化网页排名向量，并根据个性化网页排名向量对节点进行降序排序；3） 依次计算个性化网页排名向量排序中每个前缀集合的传导值，选出具有最小传导值的前缀集合作为最终的扩展集合。Cao等[18]通过最小化簇的传导值实现局部社区扩展。局部扩展中，如果节点添加到簇能减小给定簇的传导值则添加到该簇，同时，如果移除给定簇中某个节点可以减小该簇的传导值，则从该簇中移除该节点，重复执行上述操作，直到没有节点可以改变簇的传导值。

但该扩展方法对社区的内部连通性不是很敏感，在最坏的情况下，具有低传导值集合的内部可能是断开的。

9） 最大化社区权重

在Baumes等[7]提出的RaRe方法中，通过改善社区权重来实现局部扩展。在RaRe方法中，只分析在种子选择阶段删除的节点，因此只涉及添加操作。将删除节点添加到能改善权重值的社区，否则添加到与之相连的社区。重复上述操作，直到所有删除的节点都被添加到相应社区中。

在Baumes等[7]提出的IS方法中，同样是通过改善社区权重来实现。与RaRe方法不同，IS方法是针对所有节点进行分析，或添加或删除。具体过程为：① 将种子看作初级社区并计算社区的权重值；② 对所有节点进行分析生成新社区，如果节点属于给定的社区，则从社区中移除，否则将该节点添加到给定社区；③ 计算新产生社区的权重值，如果新产生社区的权重值大于原有社区的权重值，则用新产生的社区代替原有社区，否则原有社区保持不变；④ 重复上述操作，直到所有社区的权重值不再改变。实验结果证明，使用该方法获得的社区结果优于使用RaRe方法得到的结果。另外，该方法还可以改善使用其他方法得到的簇，使之成为最优的局部最优簇，例如，将RaRe方法得到的结果作为IS的输入。

为了减少 IS算法中局部扩展的运行时间，Baumes等[12]提出了改进的迭代扫描方法（IS2, improved iterative scan）。在IS方法中进行局部扩展时，每次迭代是对所有节点进行分析，而在IS2方法中，只分析了给定社区内的节点以及该社区的邻域节点，但该方法引入了寻找给定社区邻域节点的时间。当社会网络比较稀疏时，由于分析节点减少的时间大于寻找给定社区邻域节点所花费的时间，因此，IS2方法优于IS方法；当给定的社会网络密度比较大时，由于分析节点减少的时间小于寻找给定社区邻域节点所花费的时间，因此，IS方法优于IS2方法。综上，当社会网络比较稀疏时，应该采用IS2方法中的局部扩展方法，当社会网络的密度比较大时，应该采用IS方法中的局部扩展方法。

在上述方法中，每个种子在扩展时是独立进行的，因此某个节点可能被划分到多个社区，所以上述算法可用于重叠社区的发现。

3.2 基于半监督的局部扩展优化方法

基于半监督的局部扩展优化方法通过获取部分节点先验知识来指导社区发现，从而避免无监督方法的盲目性。通常考虑的先验知识包括以下2种：1） 已知部分节点的社区标签（例如种子节点）；2） 成对节点之间的必须连接和不可能连接的约束[35]。

1） 已知部分节点的社区标签

Shang等[4]提出的扩展方法是利用半监督学习技术将边划分到不同的社区中。在该扩展方法中，将种子标注相应的社区标签，并作为训练集。另外，考虑到在训练中每个社区只有一个样本，因此在实施扩展算法前，对训练集进行了扩展，将种子邻居节点之间的边标注上和种子相同的社区标签并添加到训练集中。扩展过程利用期望和最大化算法将边分类到社区中，包括2个步骤：① 期望步骤，首先利用拓扑信息确定某条边是否为给定社区的潜在边，在确定某条边为给定社区的潜在边后根据主题信息计算其属于给定社区的后验概率，并将其添加到具有最大后验概率的社区；② 最大化步骤，基于所有标注的边来评估期望步骤中的未知参数。

2） 成对节点之间的必须连接和不可能连接的约束

陈俊宇等[15]提出的SLEM。该方法考虑到事先准确知道某个节点属于哪个社区是不现实的，因此通过判断一对节点是否属于同一个社区作为约束信息来指导社区发现的执行。SLEM算法的局部扩展采用贪心策略将初始节点扩展为局部社区，通过对比与合并，得到最终的社区发现结果。

表2列出了上述局部社区扩展方法的时间复杂度。其中，Ci∈C表示生成的某个社区，C为生成的社区的集合；NCU表示生成的社区内节点的平均个数；NnE表示社区或节点的邻域的边的平均数；NlE表示给定节点所在的确定规模的局部社区内边的数量；β是给定的参数，b∈[1,■logNE■]，KZ表示支持集的规模[14]；m表示EM算法的迭代次数[4]。

由表2和上述分析可知，贪婪扩展方法有多种特征指标，但扩展策略主要分为4类，具体如下。

① 以未标记的节点为中心添加节点。这种扩展方法首先找出与未标记节点连接的种子，然后根据贪婪规则与相应的种子合并[7,12,17,24-25,27-28,31]。大多数情况下这种扩展方法的时间复杂度与网络中的边成正比，因此，更适用于密度小的网络。

② 以种子为中心添加节点。这种扩展方法首先找出种子的邻域，然后根据贪婪规则选择某个邻域节点与种子合并[6,11,19,26,33]。大多数情况下这种扩展方法的时间复杂度只与网络中的节点和邻域的平均规模有关，因此，它更适用于密度较小的网络。由于NUNnU=2NE，且通常K≥2，因此，与第一类扩展策略相比，在密度大的网络中，该类扩展方法的时间复杂度更小。

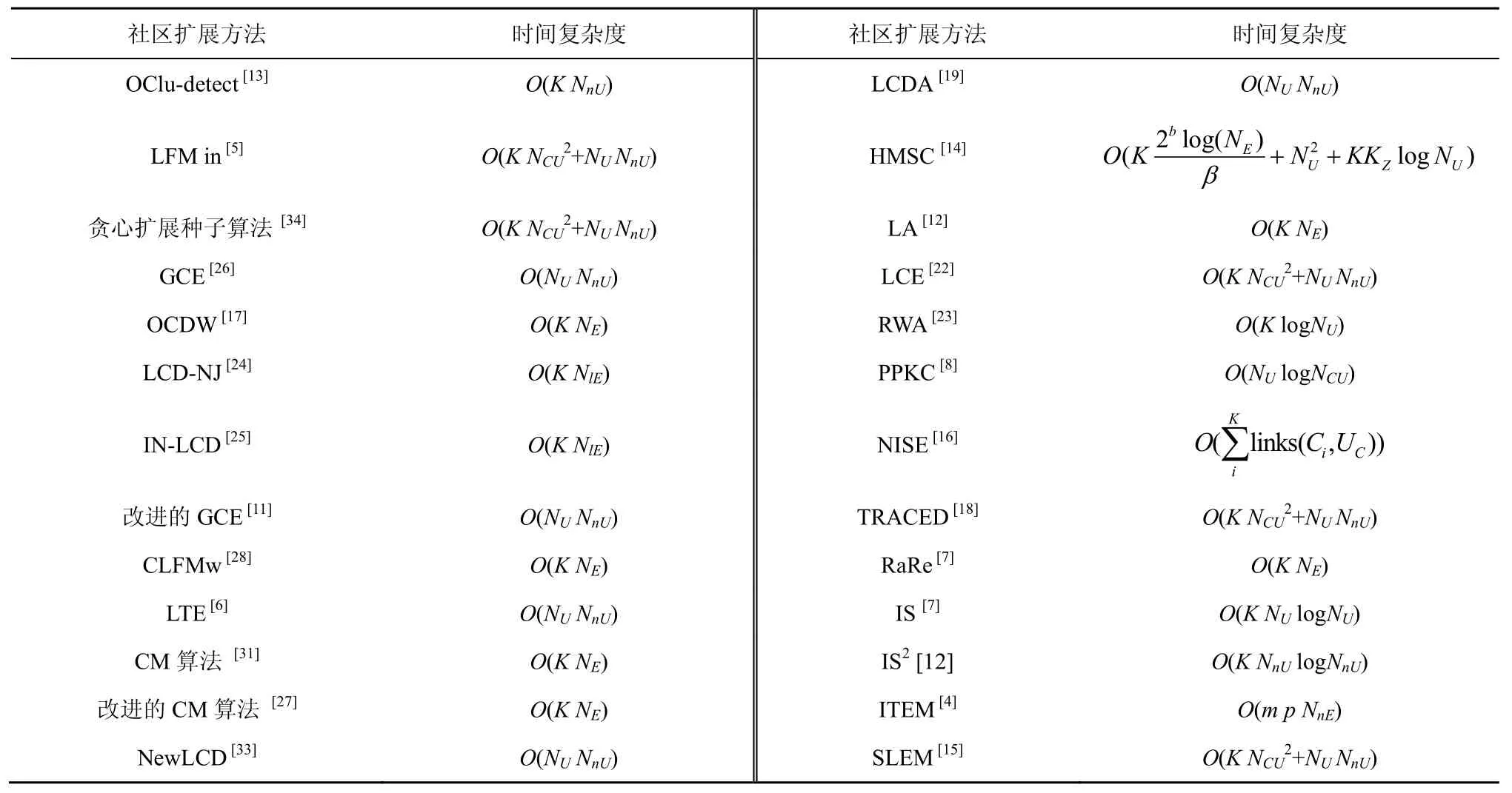
表2 局部扩展方法的时间复杂度对比

③ 以种子为中心添加或删除节点。这种扩展方法不仅根据贪婪规则选择某个邻域节点与种子合并，同时还根据贪婪规则删除已标记的节点[5,15,18,22,34]。这种扩展方法的精确度优于前两类方法，但增加了删除已标记节点的时间复杂度，因此，它适用于对社区发现结果要求高且密度小的网络。

④ 以未标记的节点为中心添加或删除节点。对于网络中的任意节点，首先判断该节点是否属于给定社区，如果属于给定社区且删除该节点能改善社区的特性则删除该节点，如果不属于给定社区且添加该节点能改善社区的特性则添加该节点[7,12]，这种扩展方法的时间复杂度只与节点的数量有关。在密度大的网络中，这种扩展方法优于第三类扩展策略。

4 评价指标

评价社区发现结果最常用的指标是模块度[1,3,29,31,36-41]。除了模块度，目前使用的评价指标还有标准互信息、F1-measure/F1-score、Jaccard系数、时间复杂度等。这些评价指标从不同的角度对社区发现结果进行评价。

4.1 模块度

模块度，即Q函数。模块度可以度量社区连接的紧密度以及社区的稳定性。模块度的基本思想是将划分社区后的网络与不存在社区结构的零模型进行比较。由于该评价指标只需社区发现的结果和不存在社区结构的零模型信息，因此当实验数据集中没有给出真实的社会结构信息时，可以使用该评价指标。Newman等[37]给出的计算式如式（1）所示。

其中，eii表示社区Ci的内部边与网络中总边数的比例，eij表示连接社区Ci和社区Cj的边与网络中总边数的比例，ai表示一端和社区Ci中节点相连的边与网络中总边数的比例，且

李建华等[1]为了便于实际计算，则将eii定义为社区Ci的内部边的数量，ai定义为一端与社区i中节点相连的边的数量。当评价社区发现结果的质量时，Q值越大越好。

然而，Q函数不适用于加权网络，为了适应加权网络，徐建民等[36]提出了扩展的模块度函数Qw，其定义如式（2）所示。其中，W表示网络中所有边的权重之和，Wi表示社区Ci的内部边的权重之和，Tc表示与社区Ci中的所有节点相邻的边的权重之和。

由于Q函数不能评价重叠社区的发现结果，因此，研究人员对Q函数进行了修改以评价重叠社区的发现结果[3,22,27]，如式（3）所示。

其中，A表示社会化网络的邻接矩阵，Avu∈A表示邻接矩阵中的元素，当节点v和节点u之间存在边时，Avu=1，否则，Avu=0；NE=|E|表示网络中边的数量；kv表示节点v的度数；表示节点v是否属于社区Ci，如果节点v属于社区Ci，则否则

然而，在重叠社区中，一个节点可能属于多个社区，因此，为了更准确地度量重叠社区的质量，对QO函数进行了扩展[15,31]，如式（4）所示。

其中，αCi,v表示节点v属于社区Ci的程度，其计算方法有多种。例如，肖觅等[31]根据节点在给定社区内连接边数的比例来计算其对社区的隶属度，即表示节点v与社区Ci连边的数量，当节点只属于一个社区时，陈俊宇等[15]引入了每个节点属于社区的数量，即表示节点v属于的社区的数量，当节点只属于一个社区时，

4.2 标准互信息

1） NMI

标准互信息度量（NMI, normalized mutual information）用于衡量社区发现结果与真实社区结构的相似度，可以度量社区发现结果的稳定性和精度[42-43]。因此，当实验数据集中包含真实的社区结构（例如，LFR（lancichinetti fortunato radicchi）基准测试网络）时，可以使用 NMI评价指标，具体定义如式（5）所示[1,22-23]。

其中，Cr表示真实的社区结构；Cf表示使用社区发现方法发现的社区结构；Nr表示真实社区的数目；Nf表示发现的社区数目；M为Nr×Nf的混合矩阵，其元素Mij表示真实社区与发现社区所对应的2个社区间共同的节点数量，当真实的社区结构和发现的社区结构完全相同时，M为对称矩阵，且当i≠j，Mij=0，当i=j，Mij的值即为社区Cr,i包含的节点的数量；Mi.表示矩阵M中第i行元素的总和，即社区Cr,i包含的节点的数量；M.j表示矩阵M中第j列元素的总和，即社区Cf,j包含的节点的数量。

当评价社区发现的质量时，I值越大，则表明社区发现的结果越准确，当发现的社区划分与真实社区一致时，I=1。

但是，式（5）不能评价重叠社区的发现结果。在重叠社区中，一个节点可能属于多个社区，为了度量重叠社区的发现结果，Lancichinetti等[5,15]对式（5）进行了扩展，如式（6）所示。

其中，X和Y分别表示Cr和Cf相关的随机变量，H（X|Y）表示X对Y的条件熵。

2）F1-measure

F1-measure是正确率和召回率的调和平均值，用于衡量给定社区发现结果与真实社区结构的相似度/相关度，可以度量社区发现结果的精度。在不同的文献中，研究人员给出了不同的命名，例如F-measure[3,23]、成对F-measure[35]、F1-measure[16]、F-score[33]、F1score[2,18,41]，在本文中，将该评价指标命名为F1-measure。计算式如式（7）和式（8）所示。

其中，precision（Cf,j,Cr,i）表示社区发现的准确率，Recall（Cf,j,Cr,i）表示社区发现的召回率，其计算式如式（9）和式（10）所示。

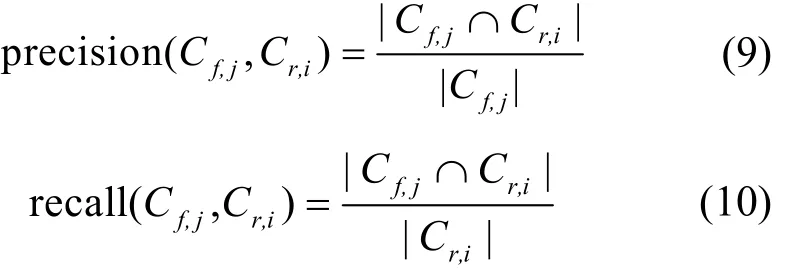
precision =Cr

∑

,i∈ Cr

Cmf,j

a

∈Cxfprecision（Cf,j,Cr,i）

（11）

Nr

recall =C∑

r,i∈ Cr

Cmf,j∈

aCxfrecall（Cf,j,Cr,i）

（12）

Nr

式（7）、式（11）和式（12）既适用于非重叠社区也适用于重叠社区。

3） Jaccard 系数

Jaccard系数与NMI的思想相同，也是通过计算社区发现结果与真实社会结构的相似程度来评价社区发现结果的质量，其定义如式（13）和式（14）所示[9]。

当评价社区发现结果的质量时，Jaccard值越大，则表明社区发现的结果越准确。当发现的社区和真实的社区完全相同时，J=1；当发现的社区和真实的社区完全不同时，J=0。式（13）既适用于非重叠社区也适用于重叠社区。

除模块度外，上述评价指标都需要数据集中包含真实的社区结构信息。然而，在爬取的网络数据中，例如Twitter、微博、微信、Facebook、大众点评、豆瓣等网络，不包含真实的社区结构。因此，在实际应用时，只能使用不需要真实社区结构的模块度进行评价。但是，在评价社区发现结果时，需要从多角度进行评价，例如精度、社区发现的稳定性、社区发现的可扩展性等。因此，需要寻求或设计更多可用的评价指标，从多方面评价真实网络的社区发现结果。

5 基于局部扩展的社区发现的应用

大部分基于局部扩展的社区发现方法的研究重点是如何更准确地发现社区结构，而对其具体的应用介绍的较少。基于局部扩展的社区发现方法不仅可以发现网络中的社区结构，有些方法还可以发现网络中全局或局部最有影响力的用户，例如基于全局排名的种子选择方法可以发现网络中最有影响力的用户，而基于局部排名的种子选择方法可以发现网络中局部最有影响力的用户。鉴于此，本文对基于局部扩展的社区发现的具体应用总结如下。

1） 社区发现方法共有的应用

这部分应用主要是将发现的社区结构应用到相应的领域，它的应用重点是发现的社区结构，而不是社区发现技术，因此，可以是基于局部扩展技术发现的社区结构，也可以是基于其他技术发现的社区结构。主要应用领域包括商业、公共安全、医疗疾病、生物学等领域[38]。

① 在商业方面的应用。社区一般是由偏好或社会背景相同/相似的用户组成的群体，因此社区发现可以应用到推荐系统中，尤其是基于协同过滤的推荐系统[44]。例如，在电子商务网站上挖掘用户需求，推荐满足用户个性化需求的产品（如电影、音乐、美食等），可以提高用户的购物体验，从而提高销售额。肖觅等[31]考虑到用户需求会受家人、朋友的影响，因此对基于移动用户行为的回路融合社区发现进行了研究；刘宇等[45]将发现的重叠社区结构作为用户群组，并根据用户对群组的隶属关系完成推荐任务；李婕等[28]通过分析用户的通话记录，建立用户间联系紧密度模型，并使用局部扩张原理和派系过滤算法进行用户群组构造以对用户资源进行了解，从而使移动运营商更好地拓展新业务。

② 在公共安全方面的应用。将社区发现应用在舆情监测、侦破案件等领域中。Bouchard等[46]对在线犯罪网络的社区发现及共犯进行了研究；丁晟春等[47]将社区结构应用在微博热点主题识别中，以实现舆情监控。

③ 在医疗疾病方面的应用。将社区发现应用在患者分类、疾病识别等方面。例如Hoshi等[48]根据发现的社区结构对患者进行分类；Mall等[49]根据社区结构对生物网络中的疾病模块进行识别；Steve等[50]则将发现的社区结构应用在复杂疾病关联分析中。

④ 在生物学方面的应用。将社区发现应用在神经、蛋白质等网络中。Becker等[30]根据蛋白质相互作用网络中的重叠社区发现多功能蛋白质；Garcia等[51]将社区发现应用在神经影像构建的脑图中。

2） 基于局部扩展的社区发现方法特有的应用

这部分应用是基于局部扩展的社区发现所特有的应用。基于局部扩展的社区发现只需要局部的拓扑结构信息即可实现，且方法简单。它可以在对实时性要强，且能获取其他信息较少的稀疏网络中有较好的应用。另外，由于局部扩展方法的特点，它在种子选取阶段有可能发现全局或局部最有影响力的用户。因此，与其他社区发现方法相比，它具有一些特有的应用。

① 在微信/QQ平台上广告推荐中的应用

在微信/QQ平台上，用户的联系人可能是家人、朋友，也可能是陌生人，所以，由微信用户构成的社会网络比较稀疏；另外，微信/QQ平台上广告上线时间短，因此获取的标签信息比较少，且对社区发现方法的计算复杂度有更高的要求。因此基于标签传播、派系过滤、边聚类优化的社区发现方法都不适合微信/QQ平台上广告的推广。因此，吴哲[52]将基于局部扩展的社区发现方法应用在微信广告推荐中。

② 在病毒式营销、产品推广、企业舆情推广中的应用

在线网络为市场营销提供了新的机遇，对于广告投放者、产品供应商来说，希望找到网络中k个影响力最大的用户作为种子节点，并通过口口相传的方法（病毒式营销）让更多用户获取信息或了解产品，从而获取最大的利益。Wilder等[32]综合随机和局部排名选取最有影响力的种子节点，以实现影响力最大化，从而促进信息的快速传播。本文中介绍的基于全局排名的种子选择方法（例如，基于节点度的排名）可以找到网络中最有影响力的用户，从而使信息在网络中最大化传播[53]。除了使用基于全局排名的种子选择方法外，也可以使用本文在局部扩展方法中介绍的贪婪算法，选择具有最大影响力范围增益的节点作为种子节点[54-56]。例如，李国良等[54]使用贪婪算法为多网络选择种子节点，并应用在病毒式营销中；马茜等[55]考虑到在产品推广过程中有些种子节点无法激活，因此使用贪婪算法发现种子节点的替代节点；为了使信息在社交网络上更好地传播，Tong等[56]使用贪婪自适应种子选择策略选择最有影响力的用户。

3） 在个性化推荐系统中的应用

在社区发现共有的应用中，当把社区结构应用到个性化推荐系统时，认为目标用户与同一社区的用户的偏好相似度比与其他社区的用户的偏好相似度高，但是无法区分社区内不同用户对目标用户的影响。而在基于局部扩展的社区发现方法中，可以发现社区中的种子节点，因此，可以利用种子节点改善推荐性能。例如，Interdonato等[57]将基于多层局部扩展优化的社区发现应用在个性化兴趣点推荐中。首先，选择受欢迎的地方作为种子兴趣点；然后根据4个数据集寻找种子节点周围的兴趣点以及兴趣点之间的距离；最后，当用户输入需求信息后，系统会以种子节点为中心，推荐满足用户需求的兴趣点。

6 基于局部扩展的社区发现的研究难点

基于局部扩展的社区发现包括种子的选取和局部扩展两部分，在这两部分中遇到的研究难点分别如下。

1） 如何有效地度量节点的权重值

全局排名、局部排名以及混合方法涉及节点的权重值，即用户的影响力。现有的方法是通过节点的中心度、网页排名等来度量节点的权重值。这些方法过于简单，有时不能准确地度量节点的权重。因此，为了准确选择种子，需要综合多种信息度量节点的权重值。另外，种子节点的选择还应该考虑具体的应用。例如，在大众点评网中，假设用户A为新用户，关注了100个用户，但没有评价过任何商家；用户B为注册已有3年的用户，关注了80个用户，评价了200家餐厅；用户C为注册已有3年的用户，关注了80个用户，评价了200家电影院。如果根据节点的中心度进行种子的选择，则节点A会被选为种子，显然是不合理的；综合多种信息来度量节点的权重值但不考虑具体的应用，则节点B和C会被选为种子；综合多种信息来度量节点的权重值且应用在餐厅推荐系统中，则节点B会被选为种子；综合多种信息来度量节点的权重值且应用在电影院推荐系统中，则节点C会被选为种子。综上可知，度量权重值的方法、应用不同，选择的种子则有可能不同，而种子的选择直接影响社区发现的结果。因此，如何有效度量节点的权重值是基于局部扩展的社区发现的难点之一。

2） 如何选择贪婪扩展算法

贪婪扩展算法通过最大化或最小化某个指标实现社区的扩展。本文中总结了现有的一些贪婪扩展指标，这些指标从不同的角度来度量发现的社区。选择的度量指标不同，则最终发现的社区也会不同。因此，如何选择合适的度量指标，使发现的社区的准确性最好也是基于局部扩展的社区发现的难点之一。

7 基于局部扩展的社区发现的研究展望

目前，对基于局部扩展的社区发现已经做了大量研究，但仍然有一些需要进一步深入探索或研究的问题。

1） 基于局部扩展的社区发现方法在移动社会网络中的应用。精确度和运行时间是基于局部扩展的社区发现方法追求的2个重要目标，然而这2个指标常常互相制约，提高精确度需要复杂的时间复杂度，而快速的运行时间则可能通过牺牲精确度来实现。随着智能终端和移动网络的完善，用户可以随时随地获取信息，因此对社区发现的实时性和精确度提出了更高的要求。为了适应移动环境，在今后的研究中，需要提出既能改进社区发现的精确度又能降低运行时间的基于局部扩展的社区发现方法。

2） 社区的初步划分。真实的社会网络中，用户数量较多，为了降低基于局部扩展的社区发现方法的时间复杂度，可以使用一些合理的规则，对整个网络进行初步划分，然后在得到的子图中使用基于局部扩展的社区发现方法。不同的网站有其独有的特点，在实际应用中可以根据网站的特点设定相应的规则。例如，在大众点评网站上，用户数量已达千万，如果直接在整个网络上使用基于局部扩展的社区发现方法，则时间复杂度会非常大。考虑到大众点评网的特点（例如用户在天津，那么他/她只会关注天津的餐厅、电影院等商家，且受天津用户的影响较大），首先根据用户注册的位置信息将整个网络划分为多个子图，然后在各个子图上进行基于局部扩展的社区发现，则可以降低时间复杂度。因此，如何设计合理的规则，对社会网络进行初步划分是一个有意义的研究问题。

3） 上下文信息的引入。目前，在基于局部优化的社区发现方法中，很少考虑用户的上下文信息，而仅仅根据用户的行为信息完成社区发现。上下文信息的引入可以更准确地度量用户在社会网络中的影响力以及用户间的影响力[58]。由于种子的选择与节点的影响力相关（如全局排名、局部排名），且社区构建和部分局部扩展方法与用户间影响力相关，因此，上下文信息的引入可以改善基于局部扩展的社区发现的准确性。如何合理地将上下文引入到基于局部扩展的社区发现是一个值得探索的问题。

8 结束语

随着社交网络、电子购物网站等的兴起，社区发现得到了更广泛的关注和研究。本文对基于局部扩展的社区发现方法的研究进展和趋势进行归纳、总结和预测，并介绍给相关研究人员，希望能为此领域及其相关研究领域（例如用户需求获取、个性化推荐、群推荐、舆情监测等）提供理论依据。