基于非合作博弈的无线传感器网络覆盖控制算法

刘浩然，赵赫瑶，邓玉静，王星淇，尹荣荣

（1. 燕山大学信息科学与工程学院，河北 秦皇岛 066004；2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004）

1 引言

近年来，随着无线通信、传感器技术及嵌入式系统的快速发展，无线传感器网络（WSN, wireless sensor network）技术成为物联网产业的重要技术之一[1]，该技术能够满足快速移动、自组织和方便快捷的需求，其发展也日渐成熟[2-3]。因此，无线传感器网络已被广泛应用到农业、医疗、工业、战场、灾难现场等领域，近五年来，更是被应用到智能交通、智能家居、智慧城市等领域，且都取得了很大的进展[4]。随着无线传感器网络的广泛应用，无线传感器网络性能中存在的一些问题逐渐暴露，有待解决。在大多数的应用中，无线传感器网络的服务质量（QoS, quality of service）成为重点研究内容，其中，网络连通性、节点电池能量利用率和节点覆盖度是当前比较重要的几个研究问题[5-6]。通常无线传感器网络节点是随机部署的，且其工作环境并非都是理想环境，因此为节点补给能量或者更换电池存在困难，同时，为了满足用户全面收集信息的需求，需要密集部署节点，因此在节点工作过程中存在节点高冗余覆盖的问题，如何合理传输数据，提高节点能量利用率成为又一大挑战[7]。针对这一问题，研究者们通常采用的解决方式有两类：分布式部署和集中式部署。集中式方法能够收集周围环境信息并给出最佳结果，但是这种方法需要所有节点都处于工作状态，即从周围环境中收集信息，并向终端转发，这将消耗大量的时间和节点能量；相反，分布式方法中，节点可以根据本地信息决定其为休眠或工作，合理调控网络状态[8]，提高节点能量使用效率。因此一般选用分布式的方法来解决网络冗余覆盖率高的问题[9]。

为解决无线传感器网络覆盖率问题，文献[10]通过确定节点的位置信息来解决节点的覆盖问题，但是该方法没有很好地解决延长无线传感器网络生命周期的问题。文献[11]提出了一种在概率模型下通过调度网络节点的通信概率和节点的工作状态来调整节点覆盖率的算法，由于无线传感器网络在节点状态转换过程中易瘫痪，因此该方法不能保证顽健性。文献[12]提出了一种基于数据感知的覆盖控制算法，该算法根据不同的数据通信量来部署网络节点，虽然克服了传统覆盖算法中无线传感器网络适应性和灵活性方面的缺陷，但是该算法在延长网络生命周期方面存在缺陷。文献[13-14]提出了一种基于潜在博弈策略空间节点决策机制和升级机制直至网络达到最优的算法，虽然所得拓扑可收集所有数据，但是存在大量冗余，消耗了大量的网络能量，不能很好地延长无线传感器网络的生命周期。文献[15]提出了一种能量感知信任衍生方案，通过管理网络开销来提高网络的节点能量利用率，同时保证无线传感器网络的安全性。但是该算法在节点部署、网络有效覆盖率方面存在问题。文献[16]提出一种分布式博弈算法，能够按照要求选取合适目标，合理地分配数据任务，该算法在应用到无线传感器网络后存在节点覆盖方面的劣势。文献[17]提出一种非合作博弈辅助拓扑控制的开发设计，节能高效，该算法能够延长无线传感器网络的生命周期，但是存在大量数据和节点覆盖的冗余。文献[18]提出了一种基于博弈的能量平衡方法，并将其应用到基于簇的路由协议中，以提高路由性能，但是存在节点分布不均，覆盖范围缺失或冗余等问题。虽然上述方法都在无线传感器网络生命周期、节点覆盖率等方面做了一些改进，但是没有综合考虑这2个相互影响的因素。

为解决网络部署过程中由冗余数据引起网络能量利用率降低、网络生命周期缩短的问题，本文提出一种基于博弈论的节点调度算法（GTCL, game theory between coverage and lifetime）。该算法引入非合作博弈理论，构造节点覆盖率和剩余能量之间的收益函数，节点通过综合考虑这两项影响因素选择合适的策略，使函数的收益较高，构建较优的无线传感器网络拓扑，使其能够尽量满足在最优覆盖率下具有最长网络生命周期。

2 问题描述

博弈论通常被用来研究某些活动的参与者行为的均衡问题，通过数学计算研究证明，从而使所有参与者做出能够获得最大利益的决策[19]，本文所提算法对网络能耗和网络覆盖率这2个方面在工作过程中联合优化：1） 在保证无线传感器网络能量消耗最低的前提下，满足网络的覆盖面积最大；2） 尽量延长无线传感器网络的生命周期，保证网络运行，防止由于节点死亡引起网络瘫痪、造成通信断路。针对无线传感器网络的这些特点，给出网络模型。

2.1 参数描述

在下文中给出3种定义来方便描述网络。

1） 节点工作能耗

无线传感器节点在工作过程中对周围环境进行感知并传输数据，会消耗大量的能量，因此将其定义为活动节点（WN, work node），节点在工作过程中的能耗为工作成本（AC, activation cost）。

2） 节点未覆盖区域

无线传感器网络的主要工作是感知和监测周围的环境，监测不到的区域就需要由其邻居节点来监测，此时，将节点的未监测面积划分为若干个小的子区域，由邻居节点来监测，这些区域称为节点未覆盖区域。

3） 冗余覆盖

如果由多个邻居节点来监测子区域，就会产生冗余覆盖（如图1所示），由此产生冗余数据，此时，节点的能耗就会大大增加。本文认为邻居节点的选择是工作节点WN的工作策略，冗余即为WN的策略选择的代价。冗余覆盖量是没有上限的，为计算方便，做如下定义，该定义参考文献[20-21]采用的方法。

其中，RCi是节点i的冗余覆盖率，是一个在 0～1之间的数；是节点i与其邻居节点j之间的子区域的面积；MRCSN是网络中一个节点可能存在的最大冗余覆盖。

图1 冗余覆盖示意

2.2 网络节点工作状态描述

假设该网络模型的所有节点均匀分布在监测区域里，且每个节点在任意时刻都处在工作状态或休眠状态，则每一个节点都只存在以下 2种策略S={DA，DI}，其中，{DA}表示节点的工作状态策略，{DI}表示节点的休眠状态策略。本文提出的节点工作博弈策略的目的是选择最少的冗余覆盖率和最大的网络能量利用率。因此定义每个节点的收益[20]为

其中，si是节点i的策略选择；v是收益概率；URi是没有被节点i的邻居节点覆盖的区域的概率；RCi是节点i的次区域的冗余覆盖区域的概率总和；AC是活动节点的能耗，如果节点进入休眠模式，而其周围没有活动的邻居节点，此时，环境中节点覆盖率为0，并且节点的收益函数为0；DA代表活动节点；DI代表非活动节点。

在节点的不同策略选择下，其收益如表1所示。

在非合作博弈中，为了找到最优选择策略，应找到纳什均衡[21]。表1显示这个游戏博弈为一个对称的博弈，该博弈的收益取决于参与者的策略。由于该博弈策略不是对称的，将节点选择的策略的概率设为分别为节点选择DA策略和DI策略的概率[20]。p的定义如式（3）所示。

其中，n为在整个覆盖区域内的节点总数。

表1 不同节点策略的收益

证明首先，计算每种策略的收益。在DA策略中，节点的收益是独立的，因此可以计算DA策略下的节点收益为

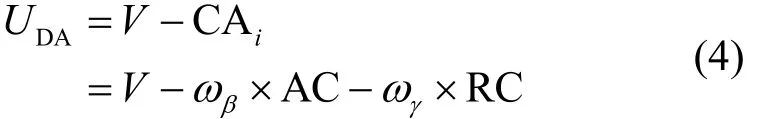
但是对于 DI策略来说，还要考虑邻居节点的策略，因此计算DI策略下的节点收益为

为找到策略效用相等的可能性，将网络中节点不同策略下的收益假设相等，从而利用均衡定义找到没有参与者改变工作策略时的概率。

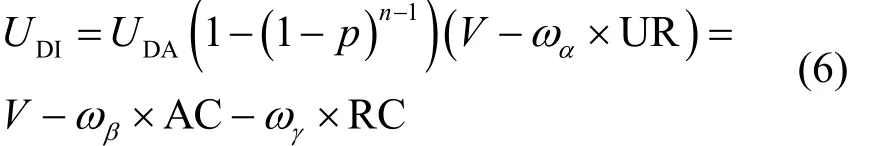
通过计算式（6）得到DA策略的概率为

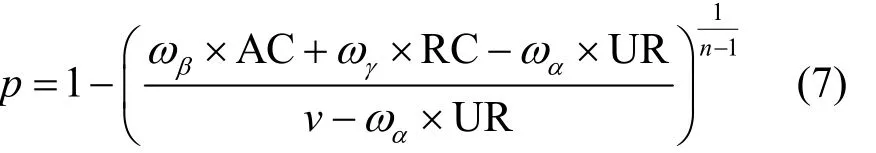
其中，αω、βω、γω为权重参数，为证明简单，本文将其均假设为1。

定理 1在所部属的网络中至少存在一个节点是活动的。

证明节点选择 DA 策略的概率p在 0～1之间，由式（7）可以看出，随着节点数的增加，概率p增加，但是至少有一个节点的激活概率不应为0。

由式（3）和式（8）可以得出，如果网络里只有一个节点，则p和p1都是 1。从式（9）和式（10）可以得出结论，当n→∞，p→0，此时p1是一个在0～1之间的数，因此证明，无论部署的节点数是多少，都至少存在一个活动的节点。

基于定理1及网络节点描述，构造网络的收益函数[20-21]，如式（11）所示。

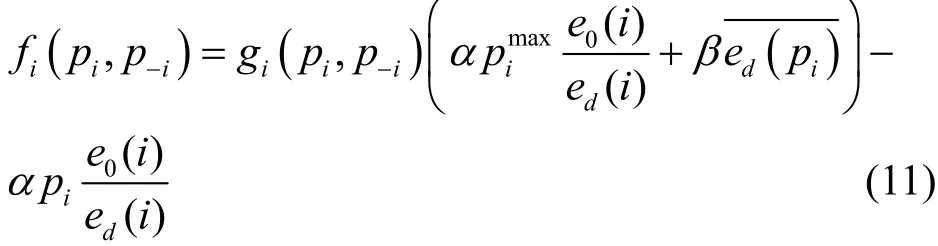
其中，α、β为节点的权重因子，均为正数；pi表示节点i的覆盖率；p-i表示其余n-1个节点的总覆盖率；表示网络的连接性，函数保证网络一直在连通中，所以节点i可通过双向链路与其他所有节点通信；e0（i）表示节点i的初始量；表示节点i的剩余能量；）表示节点为了提高邻居节点平均剩余能量，总是连接剩余能量多的邻居节点参与到网络的工作中，从而增大收益函数的收益；表示随着网络工作时间的增加，节点中剩余能量降低，此时，该部分在整个收益函数中所占比重增加，因此，当节点出现剩余能量不多，为维持网络连通且延长网络的生命周期，此时应该降低节点的能耗。说明节约节点能耗远没有维持网络连通重要。其中表示网络连通时获得的收益。

2.3 博弈模型

一方面，由于无线传感器网络对高覆盖率的需求，会产生大量的冗余覆盖，这将导致网络多余能耗增加；另一方面，过多的网络能耗会缩短网络的生命周期，而网络的生命周期是影响网络能否正常工作的重要指标，因此需要降低网络能耗，提高网络的节点能量利用率。网络中这2个相互独立又相互影响的因素符合博弈论中的策略选择的特点，因此，本文通过博弈论构建一种网络模型，在保证覆盖率情况下最大化网络生命周期。下面介绍博弈论相关算法内容。

1） 非合作博弈[21]

非合作博弈一般指在策略环境下，非合作的框架把所有参与者的行动当成是个别行动。主要强调一个参与者进行自主的决策，而与这个策略环境中其他参与者无关，既包含了冲突元素，也包含了合作元素，即冲突和合作是重叠的[22]。在WSN中，所有节点共同构成网络拓扑，同时每一个节点又根据自身的状态争取有限的资源，这一现象符合非合作博弈理论的特点，因此应用该理论解决网络中存在的问题。

在300 m×300 m的面积内无线传感器网络中随机部署N个节点编号依次为

在上述的网络模型中，网络节点选择合适的策略后，网络节点覆盖率作为该网络博弈模型的策略空间。

③ 收益函数f表示第i个参与者在策略组合选择所得的收益。

在该网络模型中，网络收益函数定义为式（11）。

4） 势博弈

一个博弈中可能不止一个纳什均衡，或者不存在纳什均衡，将至少存在一种纳什均衡的博弈状态称为势博弈。

因此，要求纳什均衡：确定一个博弈的序数势博弈，求序数势函数最大值的策略，该策略情况即为纳什均衡。

5） 帕累托最优

如果不存在一个策略s∈S使并且至少存在一个使得成立，那么策略向量s∗∈S就是帕累托最优。

3 算法实现

3.1 算法执行过程

由于该博弈算法探讨到无线传承网节点的覆盖范围，需要考虑到节点之间的空间关系，假设了解节点之间的相对位置。在算法执行过程中，节点可以计算和比较其邻居节点的局部位置。

在算法执行的过程中，每一轮都试图选择最优节点为活动节点，从而来收集周围的消息，并且这些活动节点也会根据其所处位置的邻居节点的状态，来调整自己的状态。每个节点简化为3个工作状态：工作状态、休眠状态、等待状态（此状态为非工作状态）。所有的网络节点从等待状态开始，能量较高的节点首先声明自己作为活动状态的工作节点。

通常认为节点覆盖率较优的情形是当网络最大覆盖率接近 100%时，节点能在较长的时间内地保持较高的覆盖率，则认为该节点的覆盖率较优。影响网络中节点覆盖质量的因素一般是节点的通信半径的面积、节点通信质量等因素，而并非网络拓扑中的节点数量。也就是说，在无线传感器网络中选择通信质量佳、通信半径大的节点，可以提高网络的覆盖率。为满足在最大节点覆盖率的情况下生命周期最长，该算法的执行分为3个阶段，分别是：寻找邻居节点；执行博弈，构建最优拓扑；拓扑在构建后的维持工作状态。具体过程如下。

1） 寻找邻居节点

网络中所有节点初始化，其最大的覆盖范围均相同，部署后，每个节点随机选择自身策略，同时把策略发送到初始节点，构成网络初始拓扑。

2） 执行博弈，构建最优拓扑

每个节点随机选择自己处于DI或者DA策略之后，即执行博弈阶段，每一轮只有一个节点调整自己的策略。当一个节点执行博弈之后，会向邻居节点发送广播。随着博弈的执行，网络收敛至纳什均衡。博弈执行过程如下。

① 网络中所有节点i∈N，设置参数t=0。② 节点根据邻居节点情况选择策略si，其概率为pi。

③ 其余节点state。

计算网络中每个节点的覆盖率iP。④ 计算节点收益函数。

⑤ 循环网络节点选择策略。

⑥ 收益函数收敛于某一固定值。

⑦ 活动节点构建拓扑。

⑧ 根据节点剩余能量调整策略。

⑨ 维持拓扑。

3） 拓扑维持阶段

为了保证节点在工作过程中保持能量均衡，网络拓扑中的节点总是动态地调整自己选择的策略，设定一个节点能量的阈值，当某个节点的能量低于其自身能量的30%时，重新寻找并连接邻居节点，从而使网络中节点负载更加均衡。

3.2 算法特性分析

定理2如果网络G是一个连通网络，该算法能够收敛于纳什均衡并且网络一直连通。

证明在本文提出的算法中，节点通过不断调整自己的工作状态，选择DA策略或者DI策略，来不断增加收益函数的值，直到收益函数值达到最大时，拓扑网络中节点的策略不再改变，此时，网络的状态达到纳什均衡。对于网络中所有节点来说，节点通过选择对自己有益的策略来维持节点的能耗均衡，网络连通的纳什均衡状态才有意义。

下面用反证法证明每个节点在完成自己工作状态选择策略的过程中，网络的节点覆盖率无论是从无覆盖到最优覆盖，或是从最大冗余覆盖到最优覆盖，收益函数的收益逐渐增大过程中网络一直是连通的。假设所有节点i在全部选择DA策略的时候，网络连通，当有一个节点选择DI策略时，网络不连通。

其中，α和β均为大于0的参数，且所以式（12）不成立，原命题得证。即该算法能够收敛于纳什均衡并且网络一直连通。

定理 3本文所提出的算法在网络连通的情况下收敛于帕累托最优状态。

证明由定理2的证明，该算法在博弈执行过程中网络收敛于纳什均衡，并且网络一直保持连通。首先，没有一个节点一直通过持续休眠来保持能耗效率，否则网络失连。第二，假设在保持网络连通的情况下，某些单个节点通过让自己休眠来满足增加整个网络的收益，此时，有可能会出现网络连接失效的状态或者其他节点持续工作的状态，这不利于网络收益。根据定理1、定理2描述及帕累托最优的定义可知，本文所提算法收敛于帕累托最优的纳什均衡。

4 实验仿真

为了评价GTCL算法的优化性能，本文在表2所述的实验环境下进行Matlab仿真，为保证仿真效果，将α和β的值均设定为1，形成更好的网络拓扑结构，并和文献[9]和文献[12]中提出的算法进行对比。在本文的研究模型假设中，模拟一个300 m×300 m的地下停车场模型，该环境中的照明、温控、湿度、监控等需要测控因素的传感器部署相应的网络节点。

表2 仿真环境

在监测范围内随机部署100个节点，初始网络拓扑中含有3个全连通的节点，每个新加入的节点都连接到网络中的任一节点和其邻居节点。通过执行GTCL算法生成的拓扑图如图2所示。

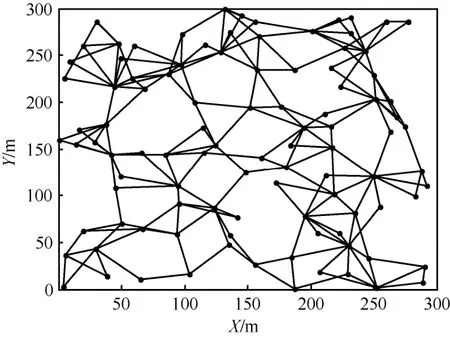
根据本文所提GTCL优化算法模拟仿真生成的网拓扑图如图2所示，在模拟环境内随机部署100个节点，某时刻活动节点互相连接，形成网络，从该网络中可以看出活动节点分布更均匀，网络的覆盖率更加合理。

构成网络拓扑后，在该过程执行算法，如图 3所示为通过 GTCL算法所体现的收益函数的收敛性，随着网络工作时间的延长，收益函数由0逐渐增加，直到收敛。从图3可以直观体现该算法所证帕累托最优存在。

图3 收益函数收敛

图4为网络冗余覆盖率，在理想情况下，网络节点的冗余覆盖率为0。但是由于网络工作过程中，节点工作区域为圆形，因此为节省能耗，存在少部分相对不重要的覆盖盲区。由图4可以看出，本文所提出的博弈论网络覆盖算法与文献[9]和文献[12]所提出的覆盖率算法相比较，文献[9]算法随着工作时间的延长冗余覆盖率更大，冗余数据更多，网络能耗更大；文献[12]算法随着工作时间的延长冗余覆盖率更小，这会导致网络数据收集的空洞；本文算法冗余覆盖率更趋近于理想值，随着时间的延长，其冗余覆盖率的变化不大，即可以保持相对较为合理的网络覆盖率和相对较小的网络能耗。

图4 网络冗余覆盖率

图5为网络相对的生命周期的对比，本文将网络剩余能量小于初始能量的15%时定义为网络失效。由图5可以看出，文献[9]所提算法由于冗余率较高，网络传输数据较多，所以生命周期最短；文献[12]算法由于网络节点部署中存在部署空洞，数据较少，网络生命周期较长；EAEM[23]模型仅以网络剩余能量作为适应度函数，几乎没有考虑网络覆盖问题；本文所提算法的生命周周期在相同环境下比文献[9]算法多工作1 300轮左右，比文献[12]算法少工作500轮左右，相较于EAEM模型本文算法少工作 1900轮左右，但是本文算法的节点覆盖率更合理。综上分析，本文所提算法更优，符合 WSN的实际应用特点。

5 结束语

针对网络覆盖率和网络生命周期这2个相互独立又相互制约的问题，本文基于非合作博弈的理论提出了一种综合考虑网络节点覆盖率和网络节点剩余能量的收益函数。通过理论证明了该模型存在纳什均衡，且存在帕累托最优。通过仿真结果表明，在保证网络连通的情况下，GTCL算法一方面能够保证网络覆盖率更为合理，另一方面有效提高了网络能量利用率，延长网络生命周期。该算法支持使用在大型停车场监测系统的网络，能够为智慧城市的构建提供理论支持。