单相永磁同步电机自学习故障检测

刘亚兵,胡利民,胡钦龙,孙红波

(中国船舶重工集团公司第705研究所昆明分部，昆明 650101)

0 引 言

单相电机以其控制简单、价格低廉、运行可靠等优点而被广泛应用在多种工业场合。对单相电机的研究，目前普遍集中在多绕组及新型结构电机领域，如Smith J M提出的SemiHex接法和SemiHexTM接法下的三绕组单相电机成为该领域近年来国内外研究的热点[1-2]。多绕组电机虽然在性能上具有一定优势，但模型及控制方式复杂，电容选取计算困难，成本不低，使用场合有限。单相自起动永磁同步电机通过在一相绕组中串入电容，在兼具普通单相电机优点的同时，还解决了后者无起动转矩不能自起动的问题，其本质上仍是电容电机。电机的平稳正常运行是系统可靠工作的前提，而及时正确地诊断电机潜在或已有的故障则是保证系统及其他设备安全运行的重要措施，文献[3]综合分析了针对电机故障而开发的传统故障诊断方法、BP网络神经法、模糊逻辑法、模糊神经网络法及遗传算法的原理及优缺点。模糊逻辑诊断方法的关键是基于模糊隶属函数和模糊规则建立起来的模糊系统，模糊规则的形成多是依赖经验及试凑，这就决定了该方法在实际工程实践中缺乏普遍适用性，而模糊逻辑法本身无法进行自学习的局限性，更是大大限制了它的使用范围。模糊神经网络法虽然具备自学习能力，但同样存在模糊系统的弊端，主观性较大[4]。基于遗传算法的神经网络在故障诊断领域有着较为广泛的应用，但选择策略、遗传算子在实际操作性极为复杂[5]，工程实现性不易。BP网络是故障诊断领域应用较多且成熟的方法[6]，由于具备强大的学习能力，尤其适用于规模控制场合[7]。

1 问题描述

本文所研究的电机应用于户外通信基站的日常维护，功率极小(18 W)。电机输出轴与毛刷连接执行正反转以刷去滤网表面的灰尘杂物，由于产品数量多，长期无人值守，当出现不可预知因素导致电机转动卡滞、堵转甚至停转故障时，要求控制系统能够通过远程通信将故障现象上报，这就对电机及其控制系统提出了几点要求：可靠性要高；成本尽可能低；具有电机故障检测能力。单相自起动永磁同步电机结构简单，控制容易，工业产品成熟，成本可控，非常适于本场合使用。通过对所购买电机实验发现，电机堵转电流与正常工作电流差异性不明显，特别是当工作电压较低时，其堵转电流甚至低于较高电压工作时的正常电流。目前常用的故障检测方式是在电机周围安装磁开关感应器，通过对电机转速进行定时计数来判断有无故障。但此方法有以下缺陷：磁开关感应器增加了成本；增加相应的固定机构，使得原先的机械组件加工安装困难；降低了可靠性。

本文所研究的故障检测方法摒弃了外围传感器，实时采集电机工作参数，依托电机数学模型，研究了一种在线自学习的故障检测方法。在众多学习算法中，1986年Rumelhart提出的BP网络神经算法是自动控制领域应用最为普遍的算法之一，尤其是在模型参数预测及故障诊断领域的应用更为有效[8-9]。本文的在线自学习的故障检测方法中，建立了电机运行过程中相关参量的BP网络神经层，通过控制误差值实现电机故障的诊断。

2 电机数学模型

单相永磁同步电机实质上是电容电动机，如图1所示，电机工作时，单相电接入OP或OQ两端，即可实现电机正反转。

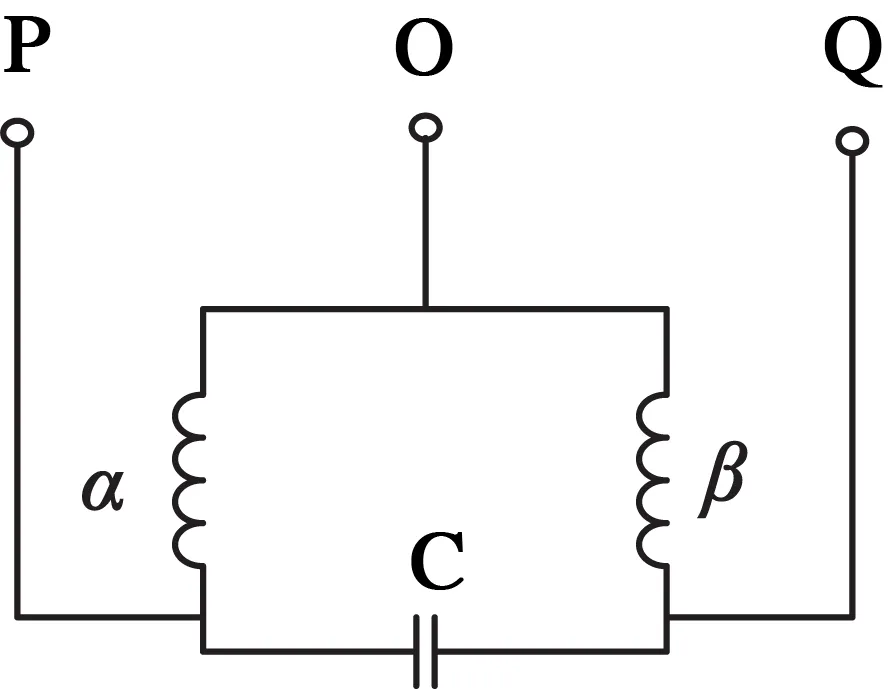
图1 单相电容电机结构图

假定OP端接入单相电时电机正转，电机定子端电压满足式关系：

U=Uα=Uβ+IβZC

(1)

式中：U为单相电电压；Uα，Uβ为α，β相相电压；Iβ为β相相电流；ZC为电容C容抗。

由于电容电机为不对称机，在进行模型分析时，需将β相绕组归算到α相，即有：

(2)

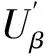
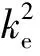
(3)

(4)

式中：Z+，Z-为电机正、负序阻抗；I+，I-为定子正、负序电流；Iα为α相相电流。

联立式(1)～式(4)，得相电流正、负序分量：

(5)

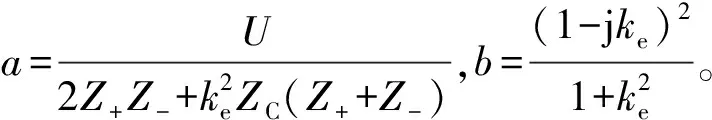
3 自学习策略

3.1 网络神经构建

自学习实际上是一个比较过程，即有实际输出信号d(k)和期望输出信号y(k)(即学习量)，两者产生的误差值e(k)去对学习系统的权系数进行修正，误差值在学习过程中逐渐变小直至为零，则实际输出和学习量一致，学习结束。

本文研究的自学习故障检测方法正是根据误差值的大小去诊断电机是否故障。如图2所示，自学习网络由2个基本的BP网络神经构成，学习量中的3个网络层为电机正常转动时的参量，实际输出量中的3个网络层由电机堵转时的参量构成，当出现有效堵转时，误差量将增大，根据该值大小可判断故障及其类型。

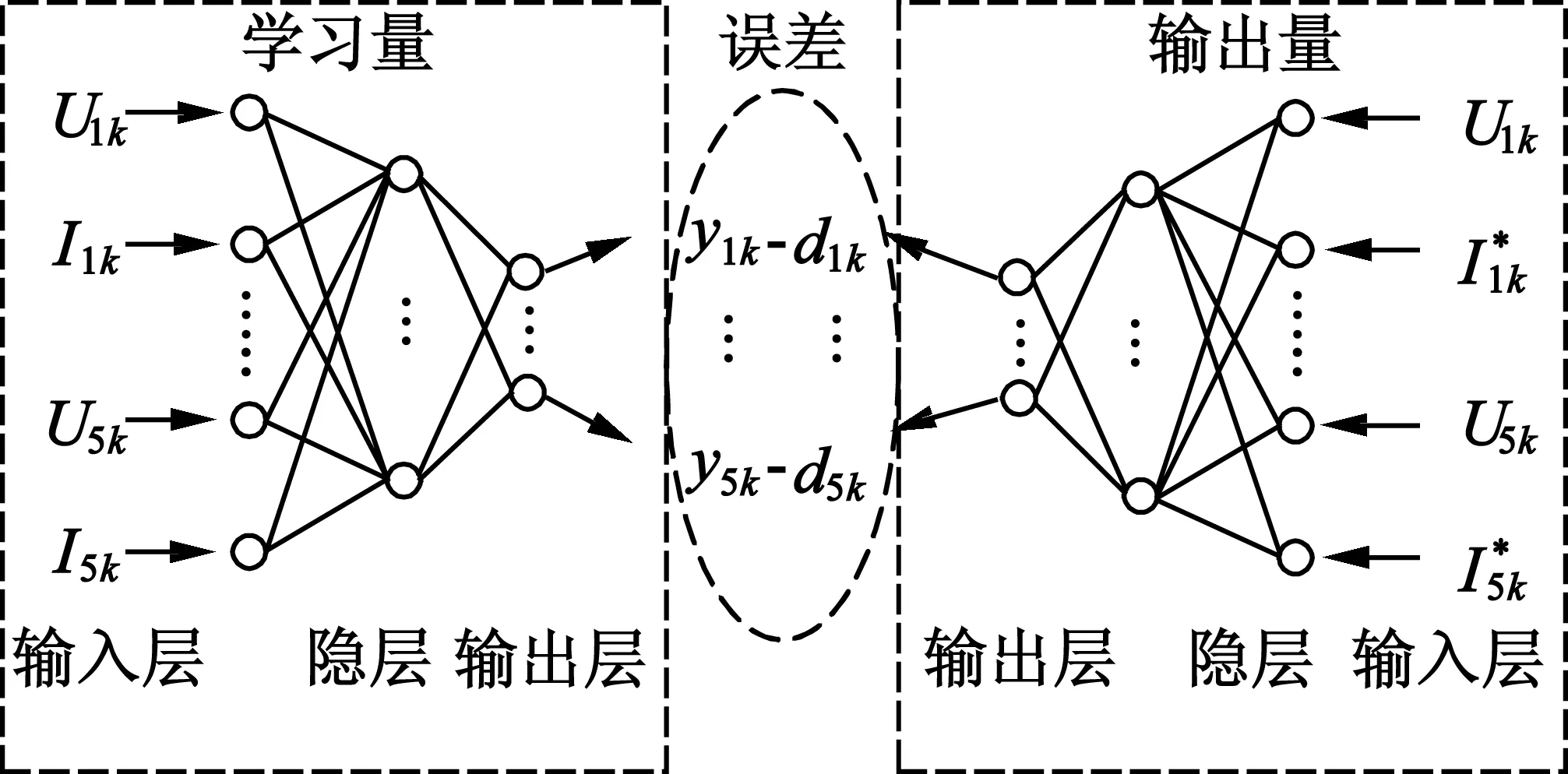
图2 自学习网络图

设输入信号为电机的工作电压和正常转动时的工作电流，即：

x(k)=[(U1k,I1k),(U2k,I2k),…,(U5k,I5k)]

(6)

输入量的权系数：

w(k)=[w1k,w2k,…,w5k]T

(7)

那么，输出信号，也即学习所得量：

y(k)=w(k)Tx(k)T

(8)

记电机堵转时的工作电流电压为实际输出的输入量：

(9)

其权系数：

(10)

那么，实际输出量：

d(k)=w*(k)Tz(k)T

(11)

输出量与学习量之间的绝对偏差：

e(k)=|d(k)-y(k)|

(12)

3.2 运行模式分析

不同电机参数不同，工作电压也随时段变化；此外随着工作时间的延伸，电机与毛刷间不可避免地出现松动，进而导致工作电流也发生变化，控制参数的不唯一性对自学习故障检测提出了必然的要求。图3给出了自学习故障检测策略下的电机运行过程图。当控制系统供电后，首先进入自学习模式，在无故障出现的情况下，电机本体参数和运行参数都将被读取、储存并作为自学习参数中的输入量；自学习结束后，进入正常运行模式，在该模式下，将时刻对运行参数进行采集，并作为自学习参数中的输出量。当电机正常转动时，式(12)的e(k)值将小于某个常量。当电机出现堵转或停转时，e(k)值将大于该常量，此时即可判定电机出现故障。需要说明的是，若在自学习模式下出现异常故障或其他自主意愿时，则可进行重复学习。

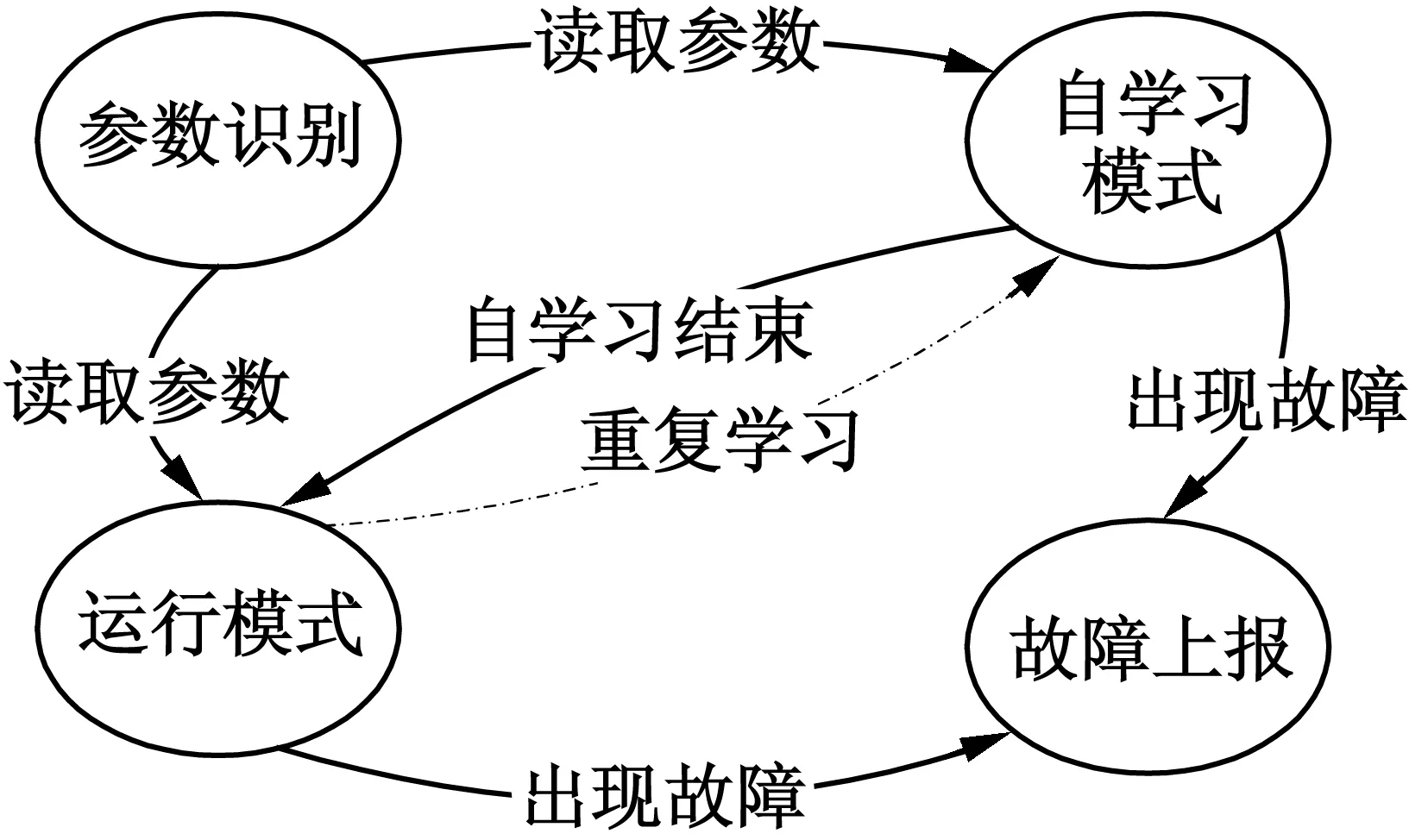
图3 电机运行过程示意图

4 实验验证

电机供电电源为普通市电，受线路用电量大小及用电时间影响，要求允许220 V(AC)存在10%大小的波动，波动程度将直接影响电机故障检测，本故障检测方案中，同时采集电机工作时的电压和电流。采集电压时，在变压器原边端串入一个保护电阻，副边经整流滤波后送入控制芯片AD端口；采集电流时，在电机绕组(图1中的P或Q)端串入采样电阻，变压器原边检测采样电阻两端电压变化，同样副边经整流滤波后送入控制芯片AD端口。

表1给出了样本电机在不同工作电压下的堵转电流和正常电流变化情况表。

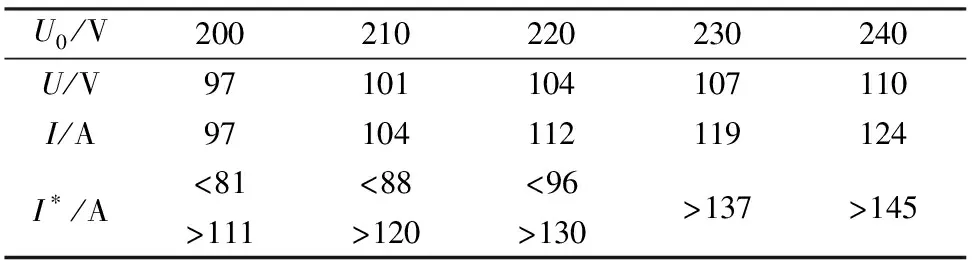
表1 不同工作电压下正常/堵转电流表

表1中,U0为工作电压值；U为电压采样模拟量值；I为正常工作时电流模拟量值；I*为堵转时电流模拟量值。

值得注意的是，在对多个电机进行了“抱死”堵转测试和间隔性堵转测试实验时，当调节电机工作电压低于额定电压后，堵转电流在“抱死”测试中反而较正常转动时变小，在间隔性堵转测试中较正常转动时变大；当调节电机工作电压高于额定电压时，只存在堵转电流增大的情况。一方面，电机转矩与相电压的平方成正比，另一方面电容电机的裂相电容也对电机性能影响较大，针对这一小功率电机堵转电流既增大又变小的“两极”分化现象，将在其他文章中再作论述。

令权系数w(k)=w*(k)，根据式(6)～式(12)，结合表1数据，即可求得权系数，代入式(12)可得：

(13)

式中：a=46，b=5 277，c=7。

当电机停转时，电流I*为零，也满足式(13)的关系。

为验证本文的自学习故障检测方法的可行性及普遍适用性，随机抽取了3个实验电机，如表2所示。3个电机功率均为18 W，裂相电容均为0.56 μF，标称工作电压为220 V(AC)。

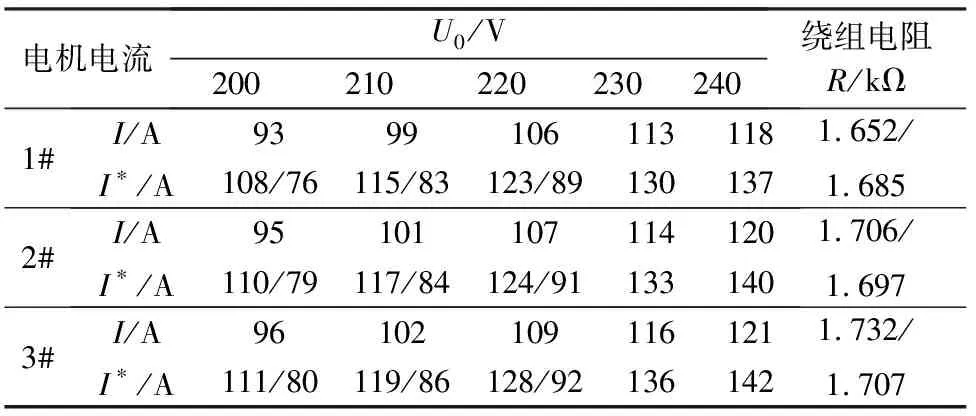
表2 实验电机运行参数表

实验中，通过调压器改变电机的工作电压，并在不同工作电压下，分别进行了堵转实验。结果显示，在不超过工作电压标称值时，3个电机均出现堵转电流“两极分化”现象；自学习过程中，控制系统根据正常转动时的电压变量，电流变量作为学习量输入，根据故障时的电压变量，电流变量作为实际输出量的输入，并以两者的绝对偏差大小作为是否故障的判断依据。由表2所列实验数据知，工作电压U0下均满足式(13)之关系，基于该故障诊断方法的控制系统能够准确地上报堵转故障；当断开电机接线端，使其停转时，也能够上报故障类型。

5 结 语

本文将在线自学习策略应用于小功率单相永磁同步电容电机，采用了BP网络神经算法，实现了电机运行故障的准确诊断。根据电容电机的不对称性，使用归算法则，将电机相电压和相电流进行了分量分解，并给出了理论值计算方法。小功率电容电机在不同工作电压下堵转电流出现“两极分化”现象的原因，除了工作电压低于额定值外，还与电机起动电容关系密切，所采取的在线自学习故障检测方法能够正确地对故障做出判断。本故障检测方法对电机参数一致性要求较低，可移植到其他电机类似的故障诊断场合。