基于时间递归平均的语音噪声功率谱估计算法研究

陈建明，梁志成，符成山

(陆军装甲兵学院 信息通信系, 北京 100072)

目前，语音增强算法中噪声功率谱估计尤为重要，直接影响着语音增强的效果，在很多单通道语音增强算法中，尤其在噪声源不可知的情况下，实时噪声功率谱估计是很重要的。例如谱减法的增益，维纳滤波的滤波系数，MMSE中的先验和后验信噪比的估计，子空间法噪声协方差矩阵等都与噪声功率谱有关[1]。同时，噪声估计作为语音增强算法的预处理非常重要，通过噪声估计可以得到语音增强算法所需要的许多相应的参数。

估计噪声的最简单的方法是1987年Kobatake[2]提出的使用语音活动检测算法，在信号的无声段(即语音间隙)来估计和更新噪声功率谱。尽管这种方法在平稳噪声(白噪声)中可以取得令人满意的效果，但是在更多的实际应用中，噪声谱特性不断变化，该方法效果表现不太理想。Martin R[3]在1994年提出基于最小统计量的噪声功率谱估计算法，该算法主要有两个问题：噪声估计功率谱因为取最小值，所以估计的噪声功率谱比实际噪声水平低以及由于平滑常数选择固定导致噪声水平的过估计。2001年Martin R[4]提出了基于最优平滑系数和最小统计量的噪声功率谱估计，基于最小统计量的噪声功率谱估计算法缺点主要有如果噪声突然变大，则需要很长时间才能跟踪上。而且当语音的持续时间超过搜索最小值的窗长，该算法估计的噪声功率谱会产生峰值。在实际应用中还存在计算量过大的问题，具有较高的时间和空间复杂度。2002年Cohen和Berdugo[5]提出时间递归平均的功率谱估计算法，该算法基于噪声对语音频谱的影响在频率上不是均匀分布的语音特性，只要该频带的无语音存在概率很高就可以对噪声功率谱进行估计和更新。此后针对时间递归平均算法做出过很多改进，Cohen[6]提出了采用两次最小值控制的迭代过程来估计，首先通过第一次平滑和最小值控制来对VAD(Voice Activity Detection,语音端点检测)进行粗判决，再用第二次平滑和最小值控制防止噪声功率谱中混入语音分量。Rachagari[7]提出采用相对简化的最小值控制估计语音存在概率的方法，首先进行最小值搜索，再使用该最小值来估计当前语音频点的语音存在概率，但是判决门限与频率有关。

本文针对时间递归的噪声功率谱估计算法对非平稳信号跟踪慢的缺点，结合装甲车内带噪语音信号的特征[8]，提出一种改进的时间递归平均噪声功率谱估计算法。

1 时间递归平均的噪声功率谱估计算法

基于端点检测的噪声功率谱估计算法由于只在非语音帧进行噪声估计，因此不适合非平稳噪声环境。基于最小统计量的噪声功率谱估计算法虽然适合非平稳环境，但是噪声突然变大，需要很长时间才能跟上。所以目前非平稳噪声环境中，主要应用的是时间递归平均的噪声功率谱估计算法。时间递归主要思路是首先通过一定时间内最小统计量作为参考，估计当前帧的语音存在概率，再通过语音存在概率控制平滑因子，最后通过平滑因子得到估计的噪声功率谱[1]。

假设带噪语音信号经过采样后为y(n)，其由纯净语音信号x(n)和噪声信号d(n)组成，假设帧长为L，即：

y(n)=x(n)+d(n)，i=0，1，…,L-1

(1)

通过对两边同时做N点离散傅里叶变换：

Y(λ,k)=X(λ,k)+D(λ,k)，k=0，1，…,N-1

(2)

其中Y(λ,k)，X(λ,k)，D(λ,k)分别为带噪语音、纯净语音和噪声第λ帧FFT之后的第k个频率分量。

带噪语音信号在单个频带的功率通常会衰减到噪声的功率水平的语音信号特性，首先进行功率谱平滑，计算公式如下[1]：

P(λ,k)=αP(λ-1,k)+(1-α)|Y(λ,k)|2

(3)

其中α为平滑常数，Y(λ,k)为第λ帧的第k个频率分量的带噪语音功率谱，P(λ-1,k)第λ-1帧的第k个频率分量的功率谱。

第λ帧的第k个频率分量的噪声功率谱估计计算公式如下[1,9]：

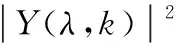
(4)

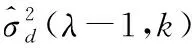
平滑因子的计算公式如下[1,9]：

αd(λ,k)=α+(1-α)p(λ,k)

(5)

其中α为平滑常数，p(λ,k)=p(H1|Y(λ,k))为第λ帧的第k个频率分量的语音存在概率，通过以最小统计量作为参考得到。

语音存在概率的计算公式如下[1,9]：

(6)

其中P(λ,k)为第λ帧的第k个频率分量的平滑后的功率谱，Pmin(λ,k)为第λ帧的第k个频率分量的功率谱最小统计量。δ为设定的阈值，如果P(λ,k)超过最小统计量乘上设定的阈值就判断语音存在，否则判断语音不存在。

语音存在概率通过下面的递归在时间上进行平滑[1,9]：

(7)

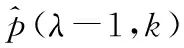
最后将式(7)得到语音存在概率代入式(5)可以得到平滑因子，再将得到的平滑因子代入式(4)得到估计的噪声功率谱。

时间递归平均的噪声功率谱估计算法具体步骤如下[1]：

步骤1：利用式(3)计算平滑带噪语音功率谱P(λ,k)；

步骤2：利用式(3)对P(λ,k)进行最小值搜索以得到Pmin(λ,k)；

步骤3：利用式(6)计算语音存在概率p(λ,k)，以及使用式(7)对p(λ,k)进行时域平滑处理；

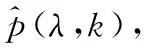
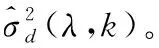
图1为时间递归平均的噪声功率谱估计算法估计的m109(NoiseX92噪声库中的坦克内部噪声)噪声功率谱与实际叠加m109噪声功率谱的某一低频段对比。其中点虚线为实际的m109噪声功率谱，实线为时间递归平均算法估计的噪声信号功率谱。图1中发现估计的噪声功率谱幅度与实际的噪声功率谱幅度相比有一定的差距，特别是当噪声功率谱幅度变化较大时更明显。因此表明时间递归平均法不能对语音噪声信号进行有效跟踪。

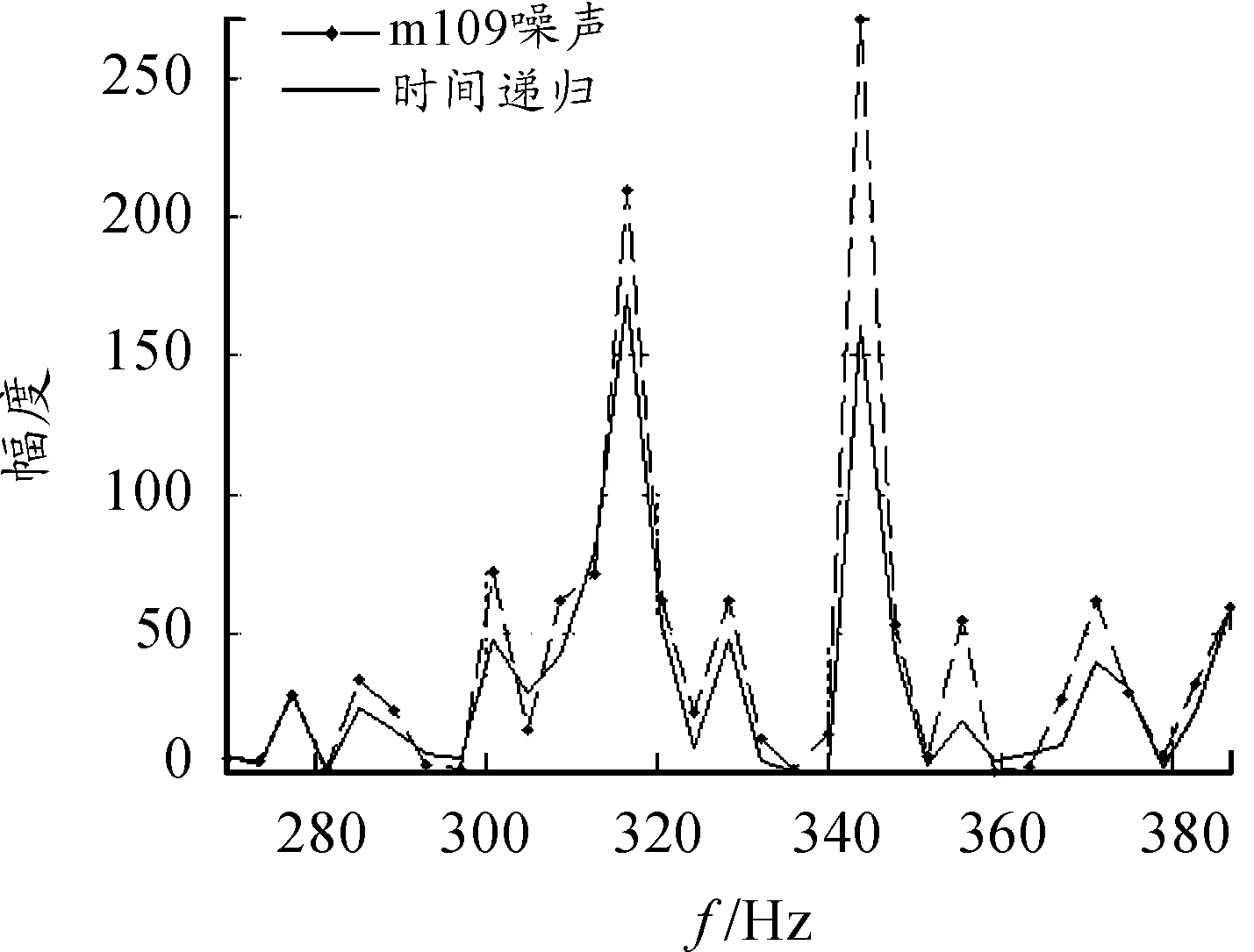
图1 m109(SNR=5dB)噪声功率谱估计

2 改进的噪声功率谱估计算法

时间递归平均的噪声估计算法对当前帧频点的语音存在概率采用硬判决的方式，然后再进行一阶平滑的方式，得到当前帧频点的最终语音存在概率。但是硬判决并没有充分利用到当前频点的信息，当噪声为非平稳信号时变化幅度较大，时间递归平均不能对信号进行有效跟踪，会产生明显的误差。文献[10]对语音存在概率估计上，对当前帧利用后验信噪比采用软判决代替硬判决，该算法很好地解决不能充分利用到当前频点的信息而导致不能对信号有效跟踪的问题，充分利用当前频点的信息，更好的对噪声信号进行跟踪。

本改进算法采用一种软判决的方法来估计带噪语音频点的语音存在概率。从统计角度看当前频点的谱熵越低，则该频点的语音存在概率越高，下一帧该频点的语音存在概率也越高，因此采用谱熵对语音存在概率进行软判决。本改进算法基于噪声变化慢于语音变化，噪声的谱熵一般大于语音的谱熵，也就是谱熵越小，语音存在概率越高，谱熵越大，语音存在概率越低。所以对语音存在概率估计上，采用对当前帧利用谱熵进行软判决。语音存在概率表达式[10-11]：

(8)

其中H(λ,k)为第λ帧的第k个频率分量的谱熵，α为控制参数。

图2为式(8)的图形表示，图中的a即α。通过图形分析可以发现谱熵越低，语音存在概率越高。当谱熵趋于0时，语音存在概率趋向于1。当谱熵趋于正无穷，语音存在概率趋向于0。这些都满足语音和噪声特性。可以通过参数α控制语音存在概率的估计大小。当α越小时，估计语音存在概率越小，反之，则语音存在概率越大。由于语音存在概率的错误类型导致的后果有所不同，即语音存在概率估计偏高，则噪声跟踪较慢，而语音存在概率估计偏低，则会出现噪声过估计现象，语音会有所损伤。因此采用双平滑系数针对两种不同的情况估计当前语音存在概率。

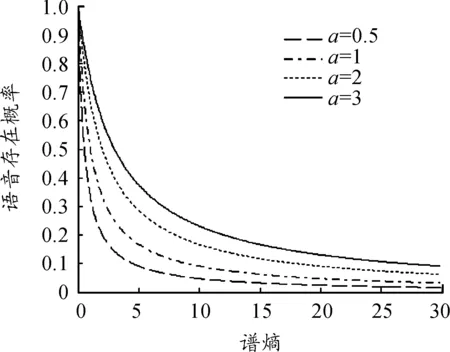
图2 谱熵与语音存在概率图

平滑后的语音存在概率计算如下：

psp(λ,k)=α(λ,k)psp(λ-1,k)+

(1-α(λ,k))psp_curr(λ,k)

(9)

其中psp(λ-1,k)为平滑后的第λ-1帧第k个频率分量的语音存在概率，psp_curr(λ,k)为第λ帧的第k个频率分量的语音存在概率，α(λ,k)为第λ帧的第k个频率分量的平滑因子。

平滑因子α(λ,k)计算公式如下：

(10)

将求得的语音存在概率代入式(5)可以得到平滑因子，进而求得噪声功率谱。

改进的噪声功率谱估计算法的具体步骤如下：

步骤1：利用式(3)计算平滑带噪语音功率谱P(λ,k)；

步骤2：利用带噪语音功率谱P(λ,k)计算得到谱熵H(λ,k)；

步骤3：利用式(8)计算语音存在概率psp_curr(λ,k)；

步骤4：利用式(10)计算语音存在概率平滑因子α(λ,k)，以及使用式(9)得到平滑后的语音存在概率psp(λ,k)；

步骤5：利用式(9)得到的平滑后的语音存在概率psp(λ,k)，计算式(5)的平滑因子αd(λ,k)；

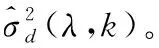
3 噪声估计算法仿真实验

3.1 仿真结果与分析

为了对本文提出的改进的时间递归平均的噪声功率谱估计算法的性能进行测试，选取一段纯净语音信号，采样频率为8 kHz，纯净语音为本文作者在安静环境下录制的男声“蓝天白云碧绿的大海”。实验中的参考噪声从NoiseX92噪声库中选取坦克内部噪声m109噪声。将纯净语音信号与参考噪声信噪比按照0 dB进行信号叠加，分别使用时间递归平均算法和本文算法分别进行噪声功率谱估计，对处理结果进行对比分析。

1) 选取m109噪声作为参考噪声信号信噪比为0 dB时，如图3所示为纯净语音按照0 dB叠加法m109噪声生成波形，图4为m109噪声频谱图，仿真结果为图5～图8。

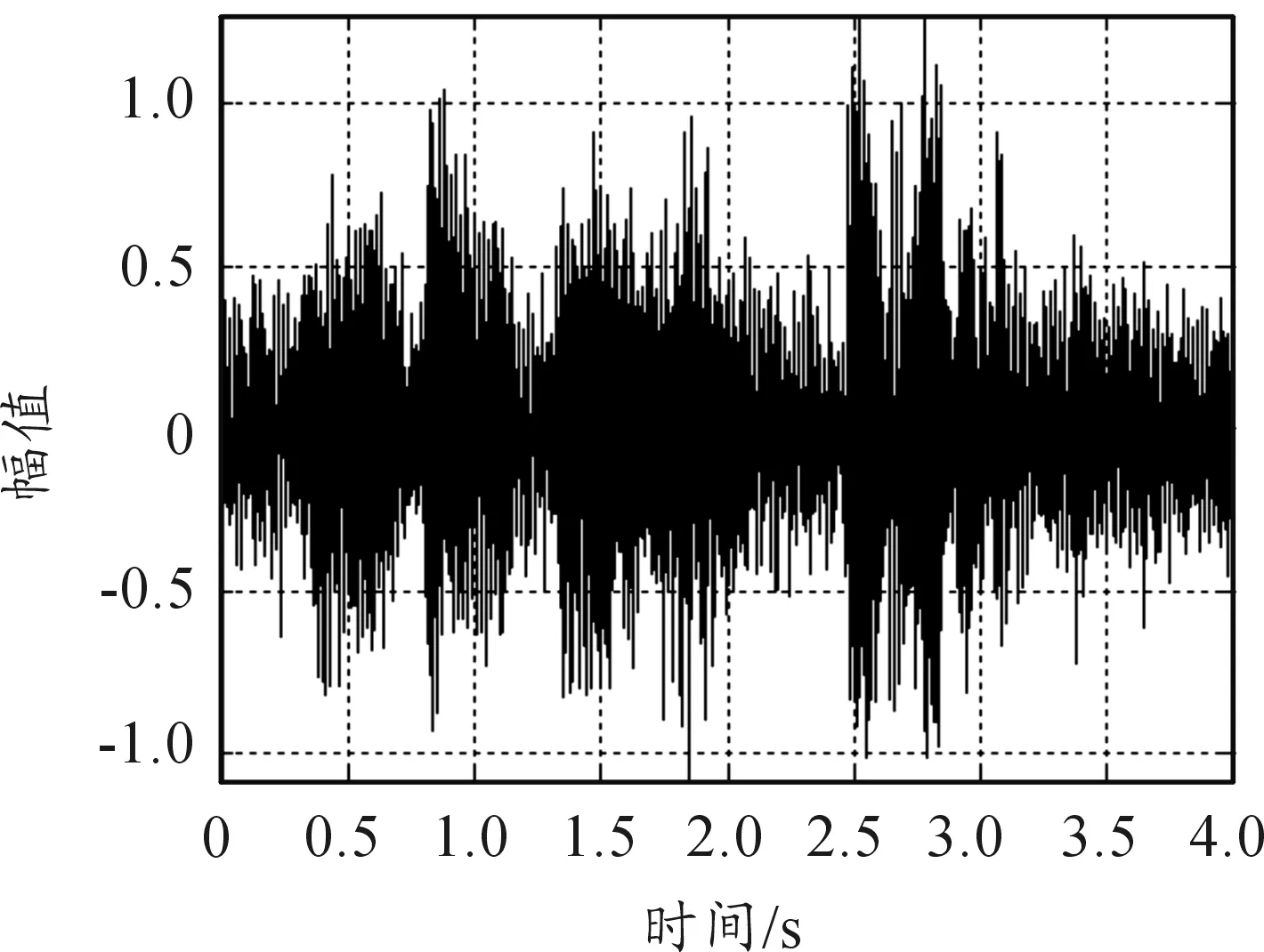
图3 0 dB (m109噪声)带噪语音波形

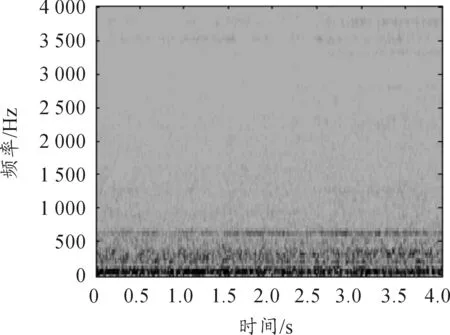
图4 m109噪声频谱图

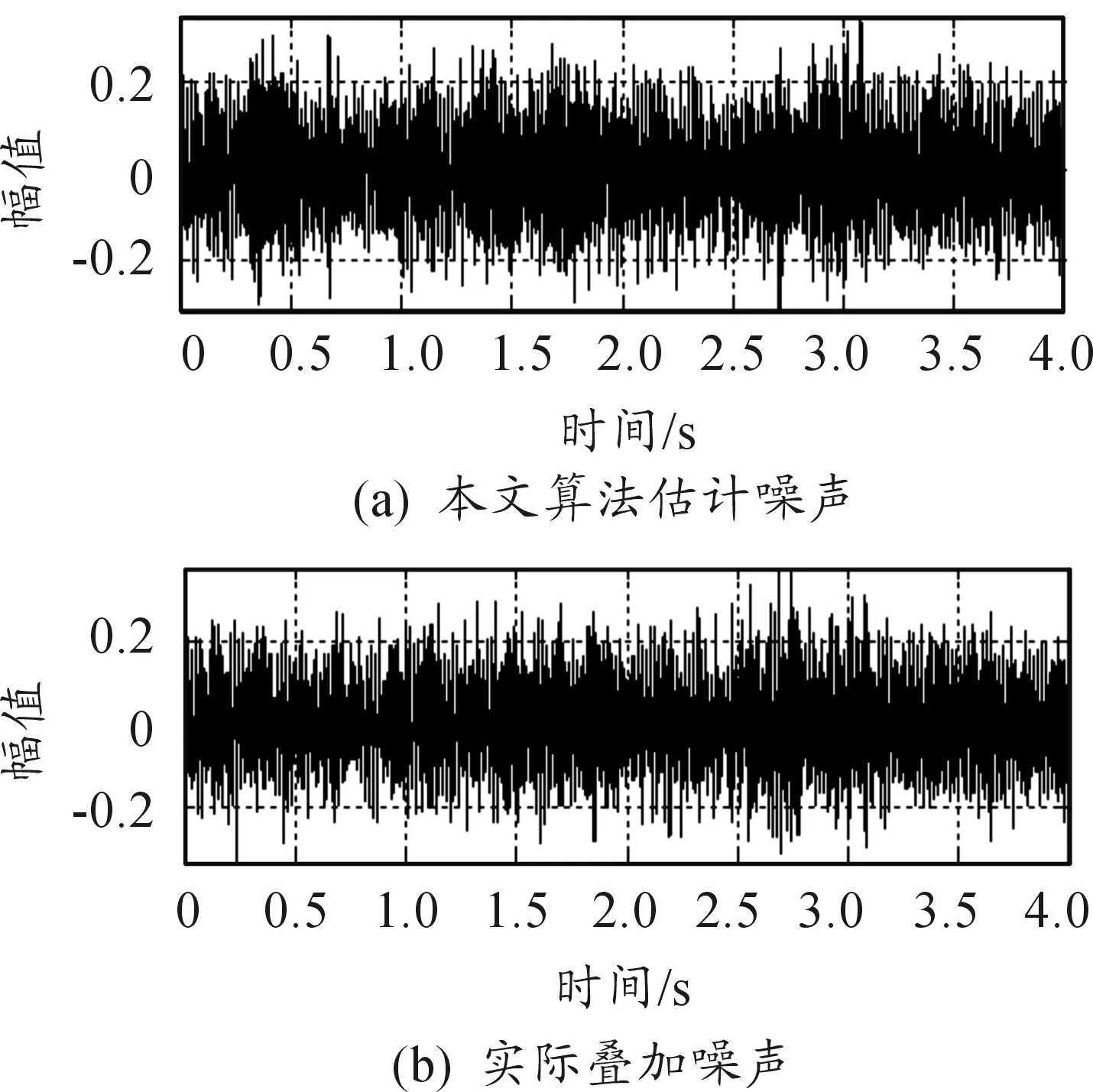
图5 0 dB(m109噪声)本文算法估计波形

图5和图6为m109噪声在信噪比SNR=0 dB时本文噪声估计算法估计的噪声波形和频谱图，可以发现波形图较好的与实际m109噪声波形重合，估计算法对噪声进行了较好的跟踪，频谱图也很好的反映了实际m109噪声频谱，估计的噪声较好。图7和图8为m109噪声在信噪比SNR=0dB时时间递归平均的噪声估计算法估计的噪声波形和频谱图，从波形图看幅度损失严重，且整体失真，频谱上在很多区域信息丢失，估计效果不理想。

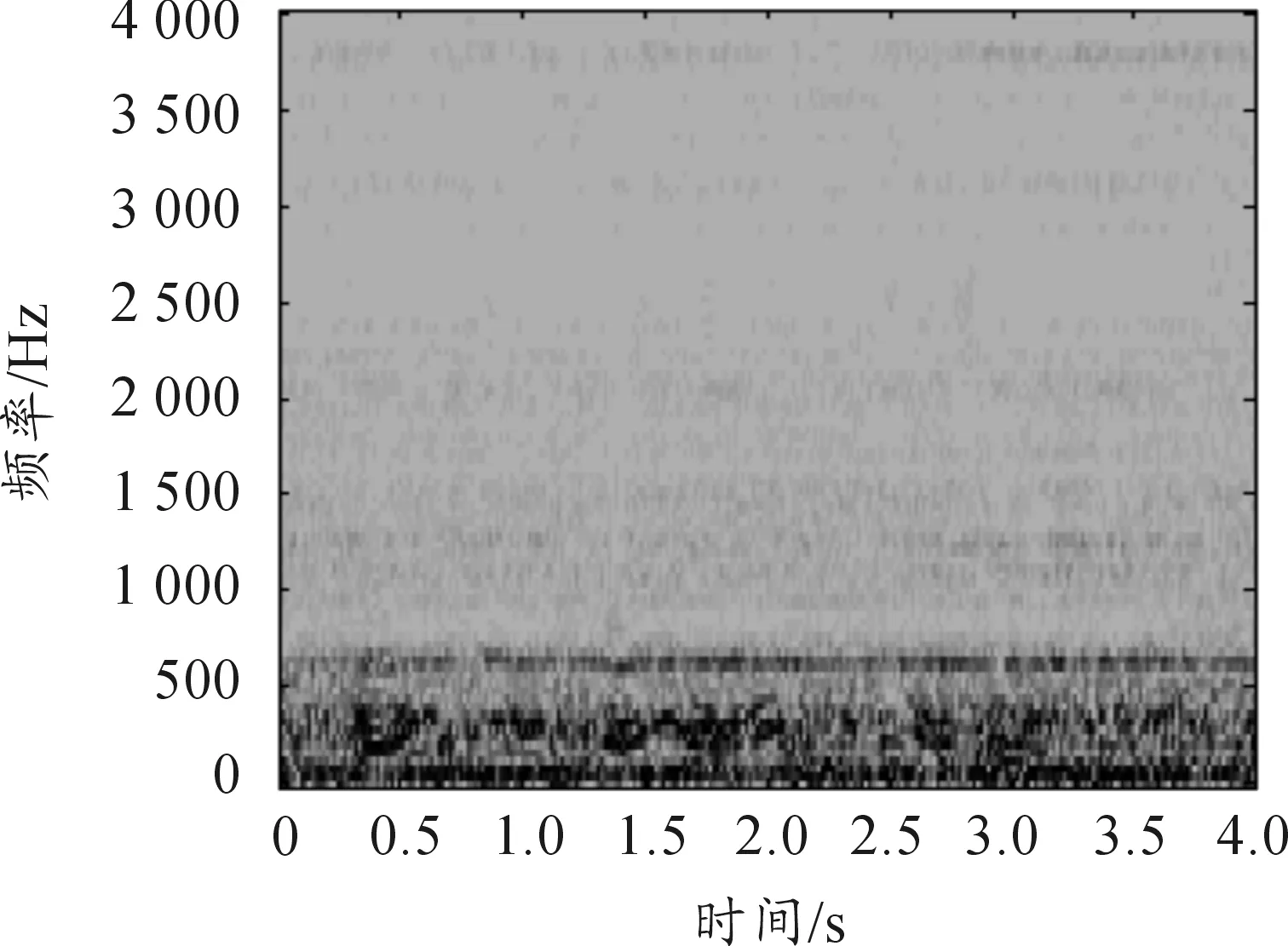
图6 0 dB(m109噪声)本文算法估计频谱

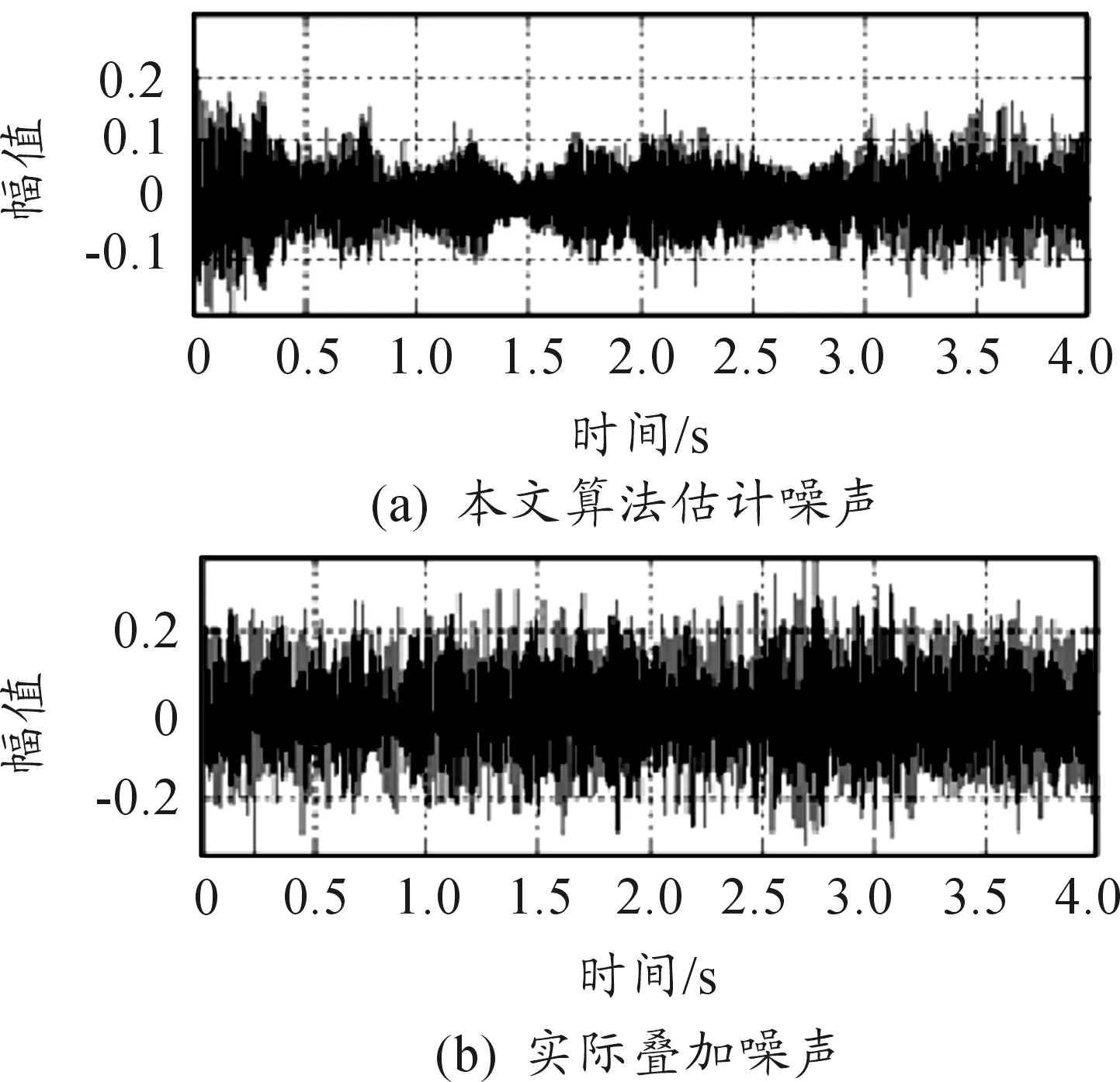
图7 0 dB(m109噪声)时间递归算法估计波形

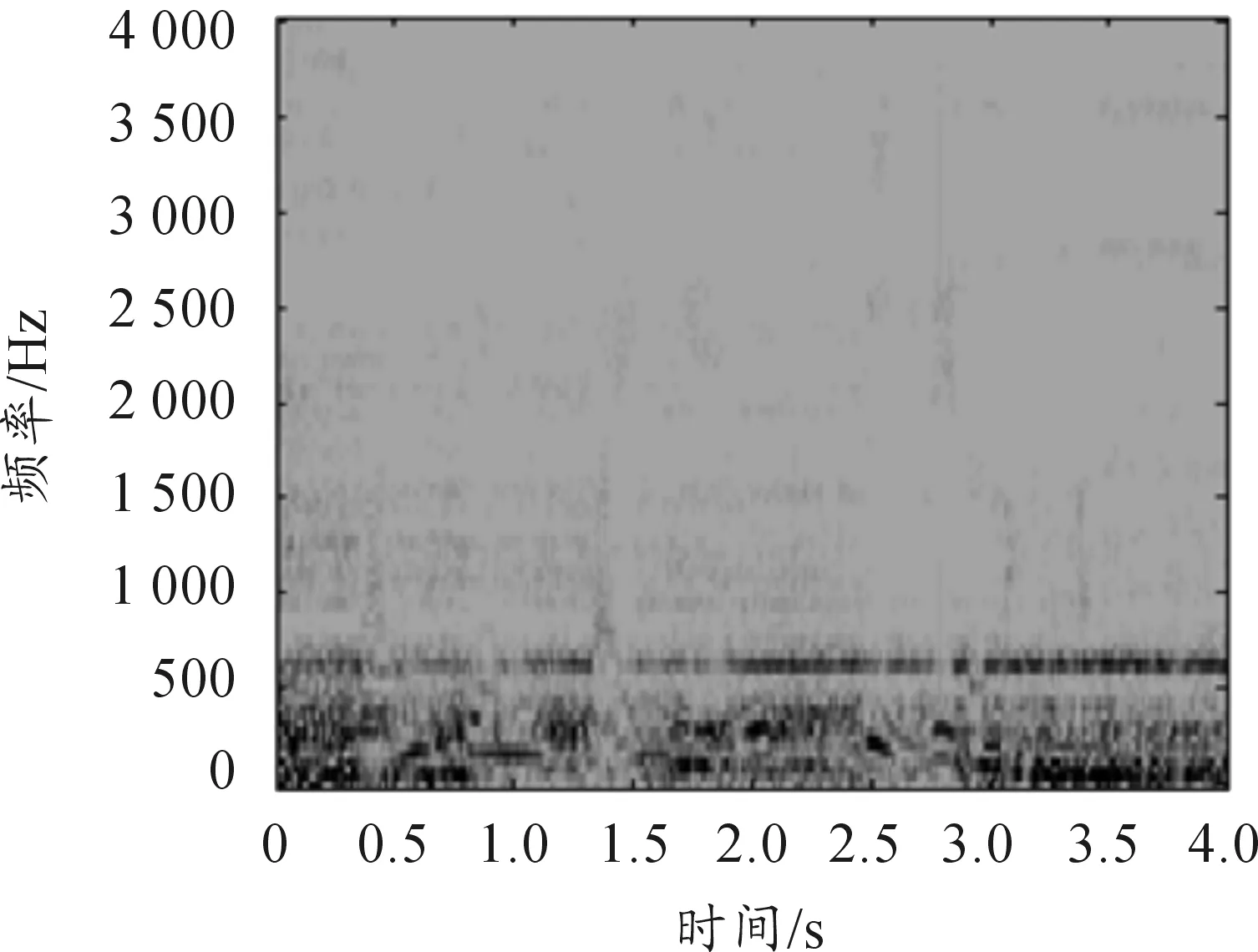
图8 0 dB(m109噪声)时间递归算法估计频谱

2) 选取m109噪声作为参考噪声信号信噪比为5 dB，对估计的噪声功率谱进行对比分析如图9所示，因为噪声普遍集中于低频段且为便于比较分析，截取了低频段的噪声功率谱估计进行分析。

其中点虚线为实际的m109噪声功率谱，虚线为本文算法估计的噪声信号功率谱，实线为时间递归平均算法估计的噪声信号功率谱。从图9中可以发现本文算法估计噪声功率谱幅度线几乎与实际噪声功率谱幅度线重合，采用本文算法估计噪声时，基本能自适应实际噪声信号的变化，这点从图5中能明显看到，当噪声突然变大也如此，而时间递归算法却有明显差距。本文算法采用自适应跟踪可以通过参数及时跟踪噪声变化，使得估计的噪声信号与原噪声信号基本保持一致。

经过以上分析，本文算法在不同信噪比下估计的噪声都很理想，估计效果明显优于改进前的时间递归平均算法，对于非平稳噪声信号，可以自适应的进行跟踪，应用效果明显，但是也存在波形幅度过估和估计小于实际噪声、频谱低频段会出现信息丢失的现象，还需进一步研究。

3.2 噪声功率谱估计算法的客观比较

一般使用归一化均方误差NMSE来评估各噪声算法性能，NMSE如式(11)所示：

(11)

客观比较采用了纯净语音，采样率为8 kHz。参考噪声信号为NoiseX92噪声库中的m109噪声和babble噪声，按照-5 dB、0 dB和5 dB进行叠加分别采用本文算法和时间递归平均的算法进行噪声估计，计算估计噪声的NMSE如表1所示。

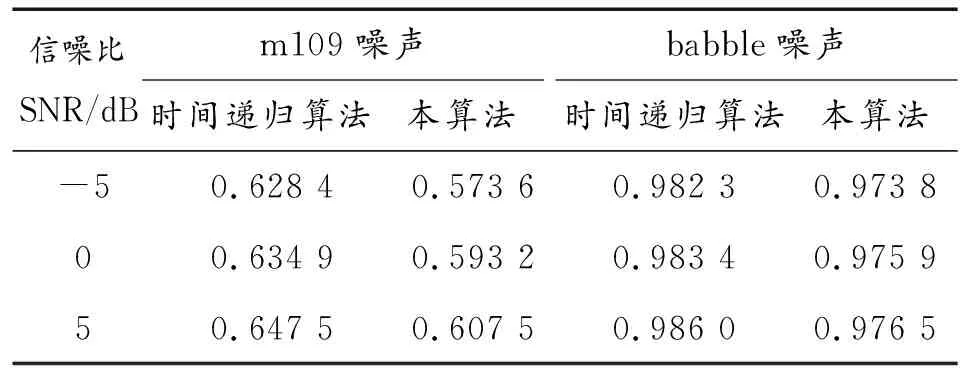
表1 本算法和时间递归平均算法的NMSE

从表1的结果可以看出：本文噪声估计算法在对m109装甲噪声和babble噪声环境下的NMSE均小于时间递归平均算法，本文噪声估计算法在客观比较上优于时间递归平均算法。

4 结论

1) 提出一种改进的时间递归平均的噪声功率谱估计算法，采用对当前帧利用谱熵进行软判决来计算语音存在概率，通过语音存在概率得到平滑系数，采用双平滑系数估计平滑后的当前语音存在概率，进而得到估计的噪声功率谱。

2) 该算法对NoiseX92噪声库中的m109噪声和babble噪声与纯净语音信号叠加形成的带噪语音信号进行仿真，在时域和频谱性能上明显优于时间递归平均算法，同时该算法的归一化均方误差也低于时间递归平均算法。

3) 该算法在仿真实验过程中，频谱低频段会出现信息丢失的现象，还需进一步的进行参数调整；下一步应用到装甲车内的真实语音信号的环境中进行更深入的研究。