弹丸挤进过程中弹带变形仿真分析
梁兴旺,李 强,安俊斌,程宇阳
(1.中北大学 机电工程学院, 太原 030051; 2.中国人民解放军75130部队, 广西 贵港 537100)
挤进过程作为身管武器发射过程的起始过程,在整个内弹道过程中占有相当重要的地位。对弹丸的发射过程来说,弹带沿膛线运动并形成刻痕为弹丸的旋转提供导向作用,并且弹丸在挤进过程中弹带的塑性变形为弹丸的沿膛运动密闭火药气体[1]。
由于弹丸挤进过程涉及高冲击、高压、高温,大变形等过程[2],因此对弹丸挤进进行试验研究是非常困难的。通常对弹带变形的实验研究主要是通过回收发射后的弹丸,例如殷军辉等[3]通过研究发射后的弹带硬度分布及组织演变规律,得到发射后的弹带宏观形变的细观与微观规律。现阶段大多数对弹带挤进过程的研究均通过有限元方法进行,王鹏等[4]采用非线性有限元方法对某大口径火炮弹带挤进过程的力学机理进行研究,得到弹丸挤进运动规律、动态挤进阻力及挤进压力值,获得了摩擦性质对弹带挤进过程的影响规律;孙全兆等[5]通过数值模拟研究弹带的动态挤进过程,分析弹带变形及刻槽形成过程;孙河洋等[6]以弹塑性有限元接触理论研究弹带挤进过程,分析了两种不同结构坡膛条件下的弹带挤进过程。
小口径火炮由于弹丸长度较短,后定心部即为弹带。弹带一般为圆柱形。为便于弹带嵌入膛线并且减少弹前空气阻力,其前后端面均设置为斜面,前方与火炮坡膛锥角对应,后方用来存放挤进过程中发生塑性流动的弹带。本文以某小口径火炮为研究对象,通过对挤进过程中的弹带受力进行理论分析以及弹丸挤进膛线过程的有限元仿真,研究弹带在挤进过程中的变形规律。
1 挤进过程中的弹丸受力分析
1.1 挤进过程中的弹带受力情况
弹丸在挤进坡膛的过程中,弹带与坡膛之间产生挤压变形,坡膛对弹带产生一定的挤压应力,弹带的受力模型如图1所示,其中α为坡膛角、β为膛线缠角;Fg为身管阴线挤压弹带的力、Fl为身管阳线挤压弹带的力、Fc为身管坡膛挤压弹带的力、Fd为身管导转侧挤压弹带的力、Fu为身管非导转侧挤压弹带的力。

图1 挤进过程中的弹带受力示意图
对弹丸所受的力进行分析,可得弹丸受到的被动力为
F=Fg+Fl+Fc+Fd+Fu
(1)
设各个接触面的面积为Sg、Sl、Sc、Sd、Su,则上述弹带所受到的力可由他们表面所受的法向应力σ、切向应力τ来表示,法向应力、切向应力之间与摩擦因素f成正比
τ=fσ
(2)
(3)
弹带在身管轴线方向所受到的力为
Fx=Fgx+Flx+Fcx+Fdx+Fux
(4)
式中,
(5)
其中n为膛线条数。
弹带在身管周向方向所受到的力为
FT=FgT+FlT+FcT+FdT+FuT
(6)
式中,
(7)
1.2 挤进过程中的弹底压力[7]
弹丸在挤进过程中受到的主动力为火药燃气给予弹丸的弹底压力,而由经典内弹道学计算出的膛内压力是膛内平均压力,弹底压力可由平均压力计算得出
(8)
式中:pd为弹底燃气压力,p为膛内平均压力,ω为装药质量,φ1为仅考虑弹丸旋转和摩擦的次要功系数,m为弹丸质量。
在已知发射药的火药特性参数后,可以通过经典内弹道学中的方法计算出膛内的平均压力,再通过式(8)计算出弹底压力。
2 弹丸挤进过程的有限元模型
以某小口径火炮为研究对象,建立其身管与弹丸的三维模型,考虑到弹丸装填时与身管坡膛之间存在一定的间隙,按照弹丸与身管的实际相对位置进行装配,如图2所示。弹丸挤进坡膛长度为10 mm,为了节约计算时间,取身管自坡膛位置起25 mm处。

图2 身管及弹丸三维模型
对建立好的身管与弹带的三维模型进行有限元网格划分,如图3所示。利用Hyper Mesh有限元前处理软件对身管、弹丸、弹带划分C3D8R网格,选用弹带为0.2 mm,身管为0.1 mm的网格尺寸方案,其中弹带网格数量为218 500,身管网格数量为3 619 680,弹丸网格数量为970 704。

图3 身管与弹带的有限元模型网格
由于在弹丸挤进过程中涉及材料的塑性流动、大变形、高应变率等非线性过程,因此弹带的材料模型采用Johnson-Cook本构模型。此外,由于在弹丸挤进过程中涉及到材料的失效及损坏,因此在材料模型中引入Johnson-Cook失效模型[8-9]。弹带材料采用紫铜,其Johnson-Cook参数如表1所示。

表1 紫铜的Johnson-Cook参数
由前述分析可知,弹丸挤进坡膛过程中受到的主动力为弹底燃气压力[10],因此对弹丸尾部横截面处施加压力载荷;身管的固定方式为炮尾连接槽固定,因此在仿真过程中,将身管尾部施加固定约束,固定其六个方向的自由度;考虑到挤进过程是两个相互接触面相互作用的结果,设置接触类型为通用接触,切向行为选用摩擦因素为0.05,法向行为选用“硬”接触。挤进过程的载荷与边界条件施加模型如图4所示。

图4 挤进过程的载荷与边界条件施加模型
3 弹带变形仿真分析
运用ABAQUS有限元软件对弹带挤进模型进行仿真分析,设置求解模式为几何非线性,并采用动力显式(Dynamic,Explicit)求解器对上述模型进行求解。求解完成后,对弹带的变形过程进行分析。
1) 挤进过程中弹带变形过程
图5为挤进过程中不同时刻弹带变形图。从图中可以看出,弹带与身管开始接触时,弹带前部逐渐挤入膛线,弹带表面刻痕逐渐形成。弹丸继续向前运动,弹带上由膛线导致的刻痕不断加深,并向后延伸。弹带材料发生塑性流动,弹带后部长度略有增加,弹丸逐渐加速,弹带后部经过坡膛结束位置后,整个挤进过程结束。总的来说,弹带刻痕的形成过程有着由浅至深、由窄到宽的特征。

图5 不同时刻弹带变形图
2) 弹带刻痕上应力分布规律
为研究弹带在刻痕位置处的应力分布规律,在弹带前部、弹带后部分别选取两条路径,路径起点为路径右端,终点为路径左端,如图6所示。分别在0.05 ms、0.1 ms、0.2 ms和0.3 ms时刻绘制两条路径上Mises等效应力曲线如图7所示,研究弹带刻痕轴向周向上应力变化规律。

图6 弹带路径示意图

图7 不同时刻弹带路径应力曲线
由图7分析得出,挤进结束后,弹带前部非刻痕处应力为310 MPa左右,刻痕底部应力为330 MPa左右,刻痕导转侧与非导转侧部位应力为350~400 MPa;弹带后部非刻痕应力约为360 MPa,刻痕中部应力约为370 MPa,刻痕导转侧与非导转侧部位应力为410~430 MPa。总体来说,弹带后部应力大于弹带前部应力,这是由于随着挤进过程的进行,弹带前部的材料发生塑性变形,被挤至后部,导致弹带后部内应力增加。此外,沿弹带周向路径,刻痕部位的导转侧和非导转侧应力比刻痕底部应力大,其中非导转侧应力略大于导转侧应力。这是由于弹丸在挤进坡膛的过程中,由于膛线的存在而使得弹带挤入膛线时与坡膛导转侧与非导转侧之间相互挤压所致,由于导转侧对弹丸导向的作用,使得弹带上导转侧材料向非导转侧流动,使非导转侧的应力加大。
3) 弹带刻痕形成过程
为研究弹带刻痕由浅至深、由窄到宽的形成过程,选取弹带刻痕导转侧和非导转侧上两条路径,路径起点在弹带前部,终点在弹带后部,如图6所示。绘制不同时刻下刻痕深度沿路径的曲线,如图8所示。
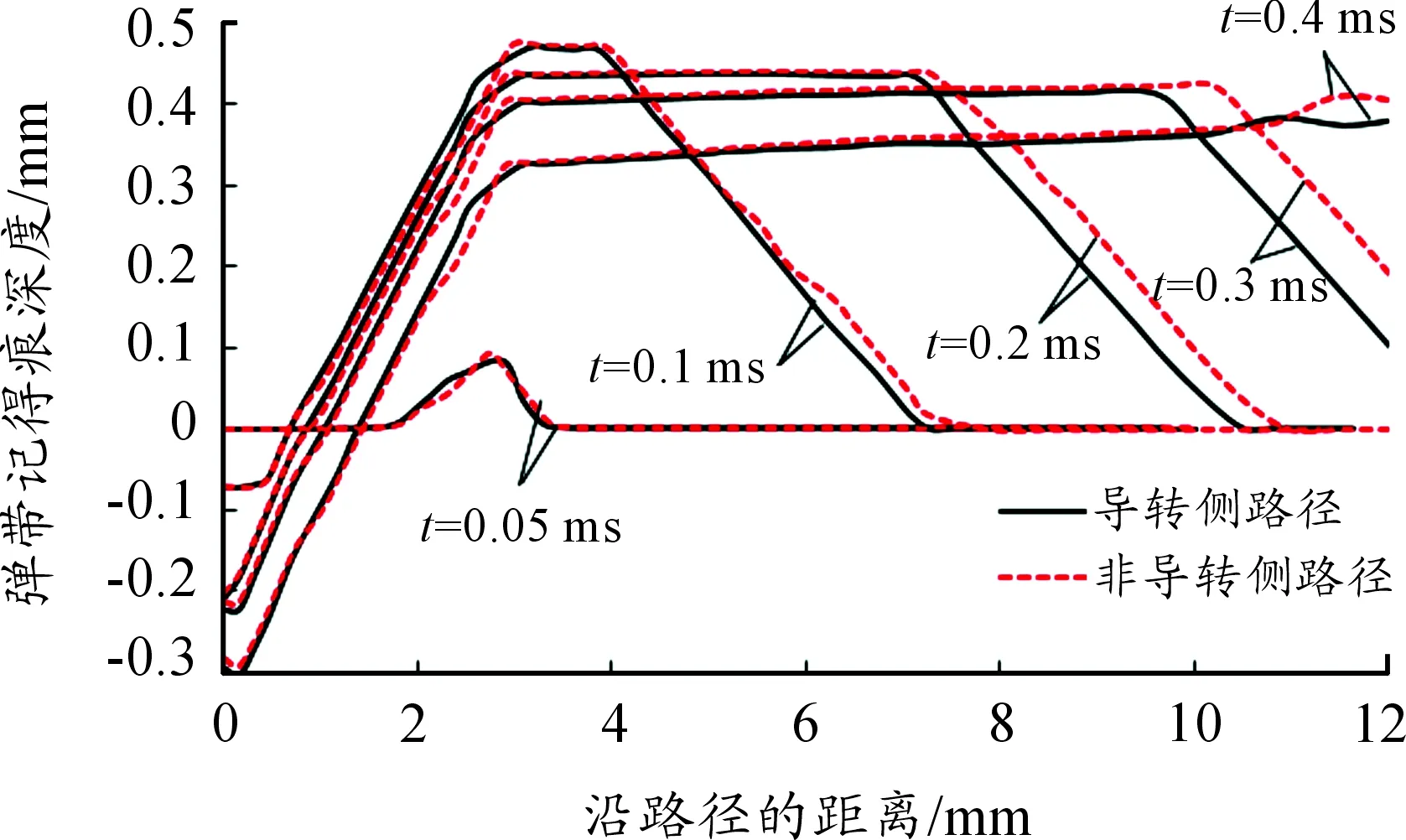
图8 不同时刻下弹带刻痕深度
从图8中可以看出,不同时刻下导转侧路径和非导转侧路径上的刻痕深度变化规律是非常接近的。弹带前部的刻痕深度由深到浅、由窄到宽逐渐成形,弹带材料在与身管接触部位向前向后均有流动,致使刻痕深度由最初为零达到最大值0.471 mm后又逐渐降低至挤进结束时降到0.332 mm。对比弹带前部和弹带后部刻痕,前部刻痕深度至挤进结束时比后部浅0.04 mm,即刻痕成形后其刻痕深度由前至后略有增加。
从弹带上由前至后依次选择a、b、c三处对其刻痕宽度进行测量,a、b、c位置的选取如图6所示。得到不同时刻下的刻痕宽度数据,见表2。
随着时间的推移,三处刻痕宽度均在不断增加,挤进结束时a处刻痕达到2.495 mm,b处为2.463 mm,c处为2.264 mm。同一时刻下a处宽度最大,c处最小。弹带刻痕宽度为前部稍宽,后部较窄。
4 结论
1) 在某小口径火炮发射炮弹时,弹带在挤进过程中的弹带刻痕形成规律为前部深度随时间由零到深再到浅,由前部至后部逐渐加深,其宽度随时间逐渐加宽,由前至后宽度逐渐减小。
2) 本文可为相关设计人员对弹带与身管坡膛的设计提供参考。

表2 不同时刻弹带刻痕宽度

