基于Simhash的大规模文档去重改进算法研究

王 诚，王宇成

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

随着大数据时代的到来[1]，数据化信息增长迅速，与此同时，数据占用空间越来越大，如此海量的数据带来了巨大的存储问题。研究发现，存储的数据中冗余数据的比例大于六成，并且接下来有继续增加的势头。冗余数据降低了用户检索和查询数据的效率，并且大量的存储资源浪费于存储冗余数据。因此相似性文档检测和去重已经逐渐成为国内外重要的研究课题[2]。

目前关于相似性文档检测和去重的主要算法有Simhash、Minhash和Bitmap[3]。文中就Simhash算法进行研究和改进，以期提高原Simhash算法的效率和准确率。

1 Simhash算法简介

传统的哈希算法通过计算将输入数据映射成特定长度的哈希值输出，输入数据的差异越大，映射出的签名值差异也越大。但传统的哈希算法，如SHA-1、MD5，对1比特差距的输入数据都会产生完全不同的输出哈希值[4]，因此无法检测出相似文档，需要对原哈希算法进行改进，使得相似文档可以输出相似的哈希值。

Simhash算法[5-6]是一种改进的哈希算法，旨在解决相似数据的去重，从而高效地识别出输入数据是否相似。Simhash算法主要有两个步骤：

第一步：hash值的计算。

首先初始化，每一篇文档内容对应一个初始化为0长度为f的签名S，和一个初始化为0的f维向量V。然后通过分词库对文档内容进行分词，过滤掉一些语气词、助词，并去掉干扰符号后将文档内容转换为一组特征词，特征词的权重为该特征词在文档中出现的次数。再将所有特征词使用相同的哈希函数映射为长度为f的签名h，遍历h的每一位，若h的第i位为1(i介于1到f之间)，V的第i位加上该特征词的权重，否则减去。最后遍历V，如果V的第i位大于0，签名S的第i位置为1，否则置为0。最终生成的签名S就是文档内容对应的Simhash签名。

第二步：对Simhash签名值使用海明距离[7]对比检索。

两个Simhash签名值的海明距离计算很容易，但当文档规模非常大时，不可能采用逐个比较的方式。对此，Google提出了解决方法，使得效率大幅提升[8]，下面举例进行阐述。

假设f为64位，如需找出海明距离小于等于3的Simhash签名，通过抽屉原理可知，平分为4个部分的Simhash签名，至少有一个部分是完全相同。因此将64位Simhash签名平分为4个部分，每部分16位，将每部分16位作为key，包含16位key的签名作为value存在Redis中。对于一个待比较的签名，使用相同方式均分为4个部分，每个部分和Redis存在的对应部分key作比较，只有这部分key完全相同的情况，才会从Redis中取出key所对应的value，并进行海明距离的计算。这种方法能够大量减少海明距离的计算量[9]。

现令k为3[10]，将64位签名平分为4部分，每部分16位，key有216个。假设数据库中已有233篇文档，每个key下平均有131 072(233-16)个签名，再来一篇新的文档需要计算海明距离数目为524 288(4×131 072)个，大大减少了海明距离的计算量[11]。

需要综合考虑空间和时间复杂度，key的位数越多空间占用越高，空间复杂度也就越高，不过，此时每个key对应下的签名越少，时间花费越少，时间复杂度也就越低。

2 改进Simhash算法

2.1 文档相似度的改进

传统的两篇文档相似度定义为，两篇文档内容对应Simhash签名值之间的海明距离。不过单一考虑文档内容比较片面，存在误差。为了减少误差，文中将两篇文档的相似度定义为文档内容的相似度和文档其他信息的相似度权重加。文档内容的相似度使用改进Simhash算法计算，文档其他信息的相似度使用最小哈希算法计算。下面给出文档其他信息相似度的计算方法。

文档其他信息包括文档关键字、文档标签、文档引用文献等，用集合的形式表示。现假设文档中所有其他信息集合为{a,b,c,d,e},文档s1含有其他信息集合为{a,b},文档s2含有的其他信息集合为{b,c,d},文档s3的集合为{a,d,e},文档s4的集合为{d,e}，将这一系列集合组成特征矩阵，如图1所示。

图1 特征矩阵

图1表示的特征矩阵的行表示文档其他信息组成的集合，列表示文档集合。计算文档其他信息的相似度，就是计算特征矩阵对应列之间的jaccard相似度。因为特征矩阵十分稀疏，使用最小哈希的方法来计算。

先对矩阵进行随机打乱，文档其他信息(即为矩阵中的对应列)的最小哈希值，为矩阵对应列第一个值为1的行号。最小哈希函数设为h，最小哈希函数用于模拟对矩阵所进行的随机打乱，特征矩阵两列之间的jaccard相似度为对应列打乱后最小哈希值相同的概率。

当特征矩阵规模很大时，对其进行随机打乱是非常耗时的，而且还要进行多次。为此使用多个哈希函数来模拟随机打乱，具体做法为：假设要进行n次随机打乱，选用n个随机函数h1,h2,…,hn来模拟这一效果，步骤如下：

SIG(i,c)表示签名矩阵第i个哈希函数在第c列上的值。SIG(i,c)初始化为Inf(无穷大)，再对r行进行以下步骤：

(1)计算h1(r),h2(r),…,hn(r)；

(2)对特征矩阵的每一列c。如果c所在的第r行为0，不做任何操作；如果c所在的第r行为1，则对于每个i=1,2,…,n，SIG(i,c)和hi(r)中的较小值设为SIG(i,c)。

计算图1特征矩阵，a,b,c,d,e对应0，1，2，3，4，5行，选用哈希函数h1(x)=(x+1)mod5，h2(x)=(2×x+1)mod5，函数中的x表示行号，遍历完所有行，最终的签名矩阵如图2所示。

图2 最终签名矩阵

文档其他信息组成的特征矩阵转化为签名矩阵，通过签名矩阵来估计特征矩阵对应列之间的jaccard相似度，也就是估计文档其他信息的相似度。最终通过文档内容的相似度和文档其他信息的相似度计算文档的相似度，将A,B两篇文档间的相似度定义为：

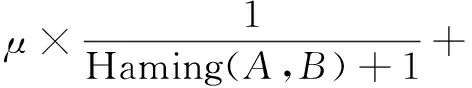
(1-μ)minHash(A,B)

(1)

其中，Haming(A,B)表示A,B两篇文档内容的海明距离，通过改进的Simhash计算得到，加一是为了保证当A,B两篇文档内容的海明距离为0时，分数不会为无穷大；minHash(A,B)表示A,B两篇文档其他信息的相似度，通过最小哈希算法计算得到；μ的取值一般为0.8～0.9，两篇文档的相似度还是以内容的相似度为主。

2.2 文档特征权值的改进

传统Simhash算法以文档分词识别出的关键词为特征值，权重为该关键词出现的次数。由于权重仅由单词出现的次数来决定，部分重要信息会丢失，导致最终计算出的Simhash签名值的准确性降低。为解决这一问题，综合使用TF-IDF[12]技术和单词的主题相关性计算关键词权重。

TF-IDF技术用于计算一个关键词在一个文档集中的一篇文档的重要性，TF表示关键词在这篇文档出现的频率，关键词ti的TF定义为:

(2)

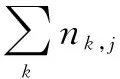
逆向文档频率IDF，表示关键词所在文档在文档集所有文档中的比重，定义为：

(3)

其中，|D|表示ti文档集中的文档总数；|{j:ti∈dj}|表示含有关键词的文档的数量(ni,j不为0的文档)。

关键词i在文档j的TD-IDF定义为：tf-idfi,j=tfi,j×idfi。TD-IDF的局限是在文档集出现次数越多，重要性就一定越小，这对于部分文档来说存在误差，有些重要单词在文档集中的出现次数也很大，需要给这些单词更大的权重。

文中使用单词的主题相关性作为附加权重，将专业术语词汇的长度作为判断单词主题相关性的依据。选用CSSCI关键词库中的关键词作为数据集，统计数据集中10 000个中文术语的长度，并进行正态拟合，如图3所示。

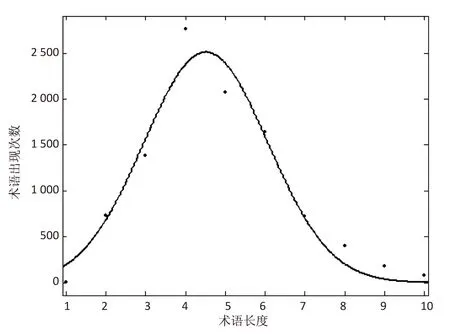
图3 中文术语长度拟合

图3所示的拟合正态分布函数为：

(4)

拟合得到的正态分布函数均值μ=4.51，标准差σ=2.207，μ的置信度为95%的置信区间[4.214,4.806],σ的置信度为95%的置信区间[1.787,2.627]。拟合得到的R square为拟合函数的确定系数，越接近1，表示拟合函数对实际数据的解释能力越好。此次拟合得到的R square为0.949 9，较接近1，说明拟合方程具有较好的解释能力。将正态分布函数归一化得到：

将归一化得到的中文术语长度函数len(x)作为单词的主题相关性函数。其中x表示单词的长度，可以看出长度越接近4.5，函数值越高，单词的主题相关性也越高。使用单词主题相关性函数作为附加的权重，可以提高TF-IDF技术判断单词权重的准确性。最终得出关键词x的权重计算公式为：

w(x)=tfx,j×idfx×(1+len(x))

(6)

其中，tfx,j×idfx为关键词x在文档j的TF-IDF值；len(x)为单词x的主题相关性函数。

2.3 Simhash签名值检索阶段的改进

Simhash签名值检索阶段使用哈希到桶的方法选出候选对，具体做法为将签名值分块，对同块的签名值使用相同的哈希函数，映射到桶，哈希到同一个桶中元素为候选对。此时可能会出现分布不均匀的情况，大量元素被哈希到了同一个桶，这个桶中的所有元素都是候选对，需要进行大量海明距离计算。

文中通过设定阈值的方法解决这个问题。当一个桶中元素超过此阈值，对桶中元素所属签名值除去桶中元素后再次分块，对同块的签名值使用相同的哈希函数，二次哈希映射仍被映射到同一个桶中元素为候选对，可以减少候选对数量，使分布更加均匀。

具体步骤为：

(1)检查每一个桶中的元素，判断元素数量是否超过阈值，阈值定义为(1+μ)×AVEn，其中AVEn为桶中元素的平均值，μ为权重。

(2)当一个桶中的元素超过这个阈值时，对桶中元素所属的签名值除去桶中元素块后，再次分块，将同一块的签名值使用相同的哈希函数，进行二次哈希，二次哈希映射到相同桶中的元素作为候选对。

例如一共有233(将近10亿篇文档)，每篇文档每部分签名为16位，则桶数组数目为65 536(216)个，每个桶的平均元素个数为131 072(233-16)个，则AVEn=131 072，现取μ为2，则当某个桶中的元素超过(1+2)×131 072=393 216时进行二次哈希，二次哈希的桶数组数目为4 096(212)个，此时依旧被哈希到同一个桶的元素作为候选对进行海明距离计算。

3 实验结果及分析

3.1 实验参数选取

仿真环境采用联想Lenovo U41电脑，处理器为Intel CORE i7，系统为64位Windows10，分词系统选用NLPIR，算法采用Java语言实现。

选择当下较为热门的互联网、医疗、教育、AI、住房五大主题作为实验数据，对原Simhash算法和改进后的Simhash算法进行对比试验。每个主题从数据库中选取1 000条相似数据，并混入5 000条不相关数据。

选用准确率和召回率来评估算法，定义如下:

(7)

(8)

3.2 实验步骤

文档集为互联网、医疗、教育、AI、住房五大主题中的1 000条相似数据和混入的5 000条不相关混杂数据。

(1)计算文档集中文档其他信息组成的特征矩阵，并使用最小哈希算法将特征矩阵转化为签名矩阵，对特征矩阵进行100次随机打乱，选用的随机哈希函数为hi(x)=(x+i)mod100(i=1,2,…,100)。

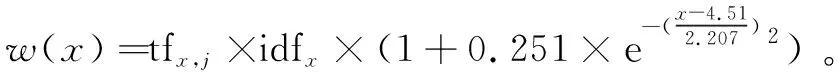
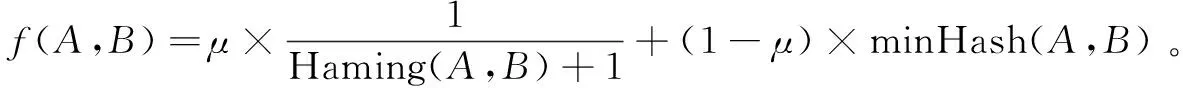
其中μ取0.9，当两篇文档间的相似度小于0.25时为相似文档。

(4)使用原Simhash算法和改进Simhash算法(第三步的文档间相似度计算方法)计算文档集的召回率和准确率。以AI主题为例，准确率的计算方法为找出的相似文档数目为分母，找出的相似文档中属于AI主题中的1 000条相似数据的数目为分子，召回率的计算方法为1 000为分母，找出的相似文档中属于AI主题中的1 000条相似数据的数目为分子。

3.3 实验结果及分析

通过图4与图5可以发现，改进的Simhash算法具有较高的准确率(约94%)和较高的召回率(约92%)。

改进的Simhash算法从多个维度，包括文档内容、文档关键字、文档标签、文档引用文献等综合计算文档的相似度，所以准确率较高。该算法综合使用TF-IDF技术和单词的主题相关性计算关键词权重，所以召回率较高且波动很小。

为研究算法效率，每秒的数据访问量不断增加，比较原Simhash算法和改进的Simhash算法的执行时间，如图6所示。

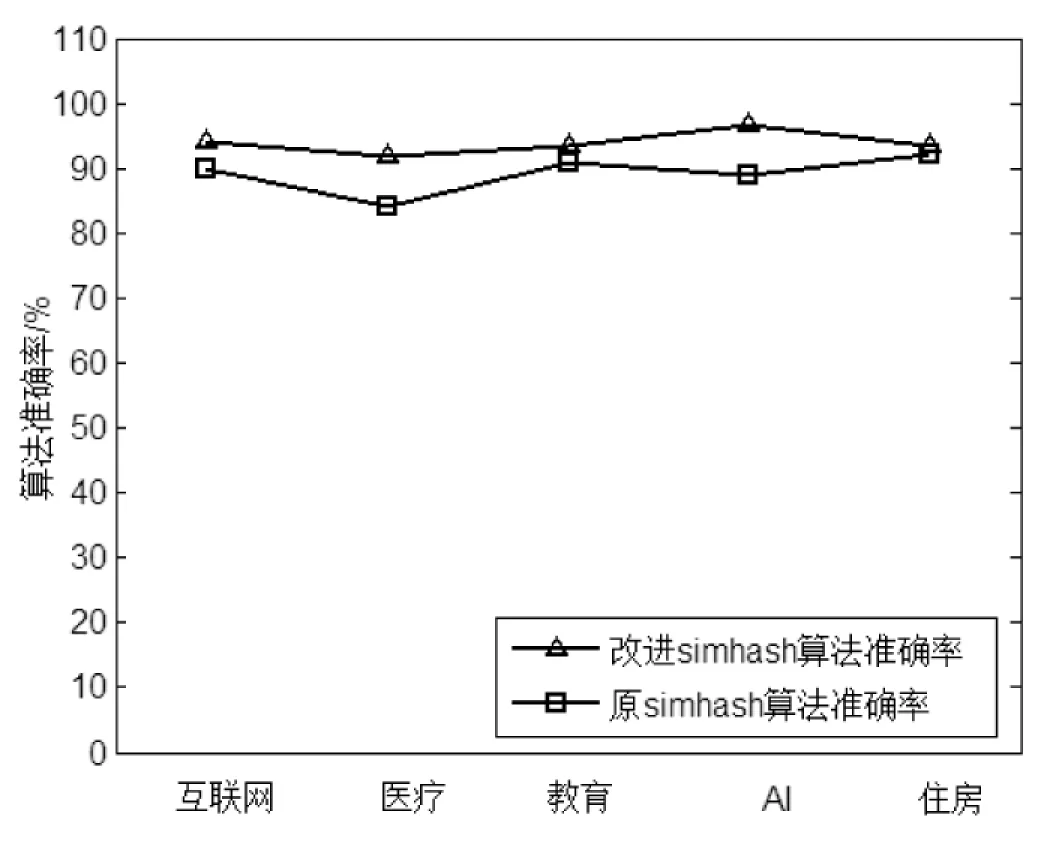
图4 准确率对比

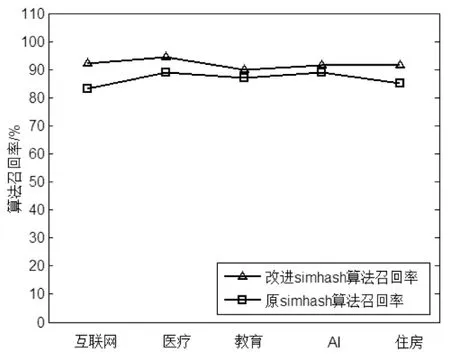
图5 召回率对比

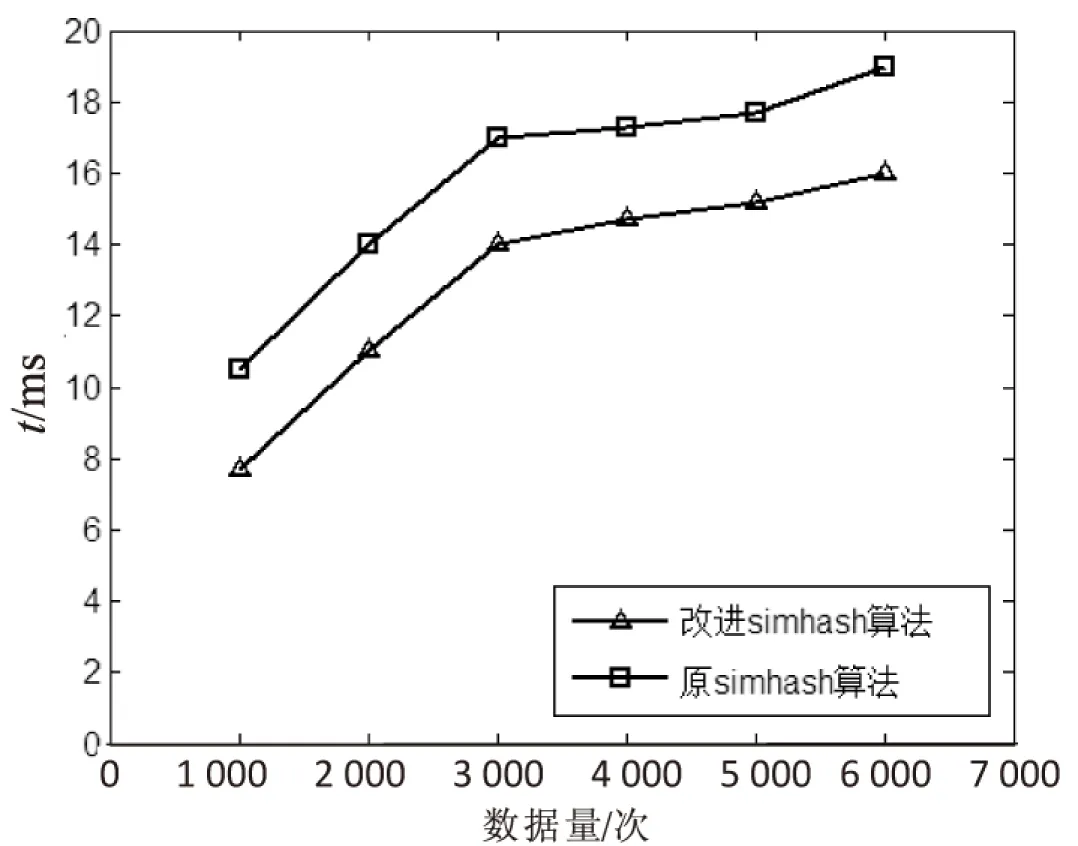
图6 执行时间对比

可以看出，改进Simhash算法由于在检索步骤中，在哈希到桶的时候应对分布不均匀的情况进行了二次哈希，减少了候选对的数量并且使分布更加均匀，可以在较短的时间内完成相同的数据量，因此执行效率较高。

4 结束语

基于Simhash算法的思想，提出了一种改进的Simhash算法，优化了文档的相似度和关键词权重的计算方法，并且在哈希到桶的时候应对分布不均匀的情况，进行二次哈希，减少候选对的数量并且使分布更加均匀。实验结果证明，改进Simhash算法提高了原Simhash算法的准确率和召回率，并且执行效率较高。改进Simhash算法具有一定的可行性，可以给相关应用提供参考，可以提高相似性文档检测和去重的效率和准确率。