压电陶瓷作动器的率相关迟滞建模与内模控制

贾高欣，王贞艳

(太原科技大学 电子信息工程学院，山西 太原 030024)

0 引言

压电陶瓷作动器具有能量密度大，响应速度快，位移分辨率高等优点，在快速控制反射镜[1]，扫描隧道显微镜，精密定位等方面得到了广泛的应用。然而压电陶瓷作动器的率相关迟滞性直接降低了控制系统的定位精度，甚至导致系统不稳定，严重影响了压电陶瓷作动器在工程领域的应用。

传统迟滞非线性系统建模方法有Preisach 模型[2]、Prandtl-Ishlinskii(PI)模型[3]等算子模型及Jile-Atherton(JA)模型[4]、Duhem模型[5]等物理模型，都是率无关的模型，不能够精确描述率相关的迟滞非线性。因此，国内外学者对率相关迟滞性的建模做了大量的研究：

1) 通过对传统静态迟滞模型的改进得到可以描述率相关性的Preisach 模型[6]、PI模型[7]、Bouc-Wen模型[8]等。

2) 将系统的静态迟滞性与率相关性分别由不同的模型表达，如Hammerstein模型[9]、三明治模型[10]、Wiener模型等。

在迟滞非线性控制方面，主要是采用逆补偿控制结合比例、积分、微分(PID)控制[11]、滑模控制[12]、鲁棒控制[13]及智能控制[14]的复合控制方法。通过迟滞逆模型补偿系统的迟滞非线性，将系统近似作为线性系统，再结合其他控制方法实现对系统的精密跟踪控制。

本文提出了一种基于广义Bouc-Wen模型的Hammerstein率相关迟滞非线性模型，分别用广义Bouc-Wen模型和自回归历遍模型(ARX)来表示模型的静态迟滞部分和线性动态部分。在所建模型的基础上设计内模控制策略，实现对给定频率范围内单频率和复合频率信号的跟踪控制。

1 压电陶瓷作动器的率相关迟滞模型

压电陶瓷材料具有率相关迟滞非线性(见图1)，即迟滞系统的输出不仅与现在的输入及其历史状态有关，还与输入信号的频率有关。

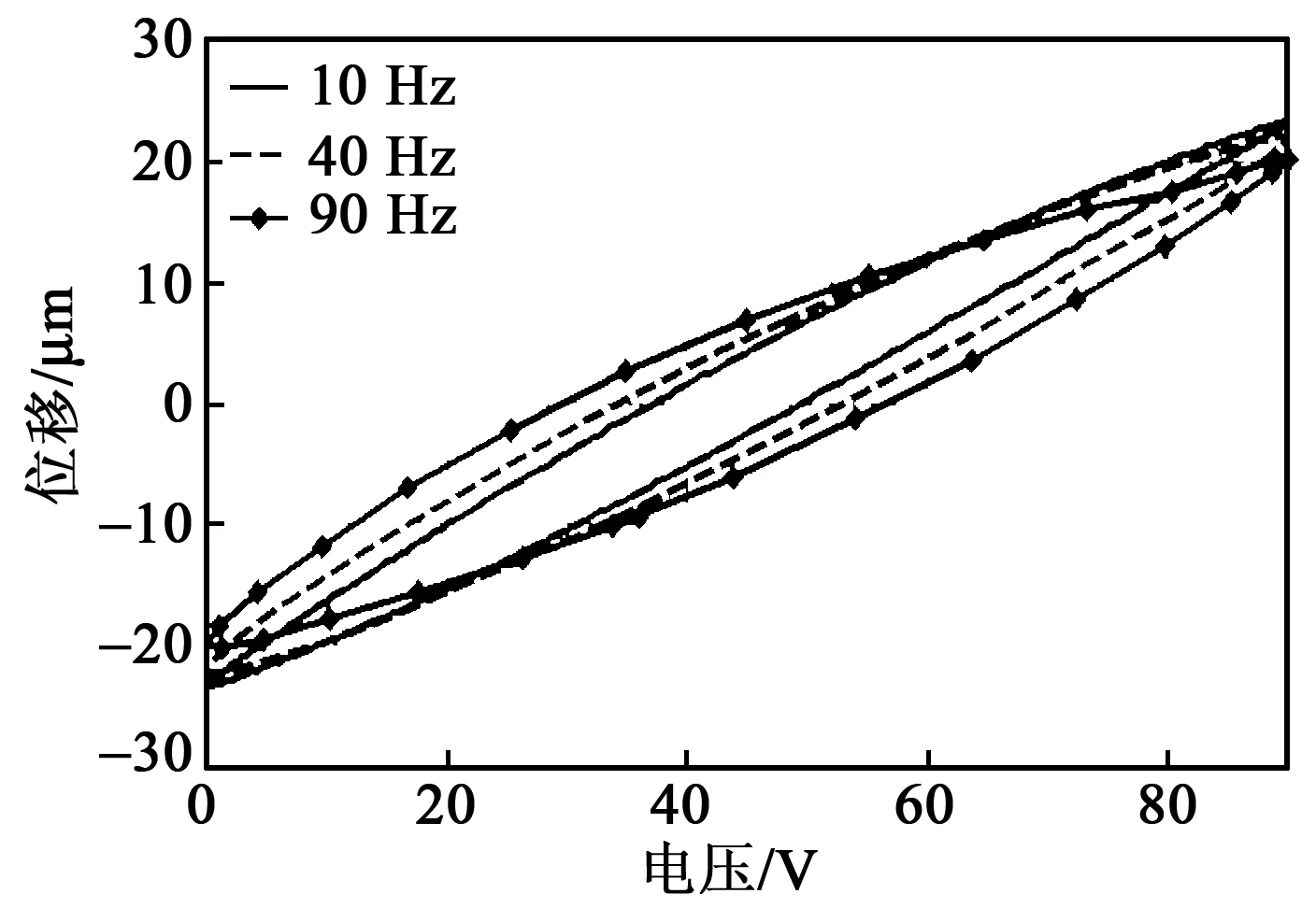
图1 压电陶瓷作动器的率相关迟滞非线性

1.1 Hammerstein率相关迟滞模型

Hammerstein模型是一种基于块连接的非线性模型，由一个静态非线性模块后接一个线性动态模块构成[15]。对于压电陶瓷作动器，当输入信号频率较低时，迟滞环曲线几乎不发生变化，可以近似认为是率无关的，即静态迟滞系统，可以由静态迟滞模型来表示。当输入信号频率较高时，压电陶瓷作动器将表现出率相关性，用一个高阶微分方程表征。为了描述压电陶瓷作动器的率相关迟滞非线性，本文提出一种基于广义Bouc-Wen模型的Hammerstein率相关迟滞非线性模型。由广义Bouc-Wen模型来描述Hammerstein模型的静态非线性部分，由ARX模型来描述线性动态部分，模型结构如图2所示。图中，N(·)为模型的静态非线性部分，G(z)为线性动态部分，u(t),y(t)分别为系统的输入与输出，x(t)为不可测的中间变量。

图2 压电陶瓷作动器的Hammerstein模型

1.2 广义Bouc-Wen模型

广义Bouc-Wen模型是由Song和Kigureghian提出的一种改进的模型以描述非对称的迟滞曲线，属于静态迟滞模型。用以描述压电陶瓷作动器Hammerstein模型静态迟滞部分的广义Bouc-Wen模型是由一个线性位移分量和一个迟滞位移分量组成的，其表达式为

(1)

1.3 ARX模型

本文用ARX模型来描述压电陶瓷作动器的线性动态特性。

ARX表达式为

A(z)y(t)=B(z)u(t)+ε(t)

(2)

其中

A(z)=1+a1z-1+a2z-2+…+anz-n

(3)

B(z)=b0+b1z-1+b2z-2+…+bmz-m

(4)

式中：ε(t)为误差项；z-1为单位延迟算子。

ARX模型写为传递函数形式为

(5)

2 模型的辨识与检验

2.1 模型辨识

基于广义Bouc-Wen的Hammerstein率相关迟滞非线性模型参数辨识，需要两步来完成，即

1) 广义Bouc-Wen模型辨识。多次实验结果表明，当输入电压频率小于1 Hz时，作动器的迟滞环曲线几乎不发生变化。所以，这里采用在1 Hz信号激励下的压电陶瓷作动器输入数据u(t)、输出数据y(t)，通过差分进化算法来辨识广义Bouc-Wen模型。定义性能指标为

(6)

(7)

式中：RMSE和RE分别为作动器实际输出和模型输出的均方根误差和相对误差；L为数据长度;yexpi为第i个采样时刻作动器的实际输出；yi为第i个采样时刻模型的输出。

基于差分进化算法得到广义Bouc-Wen模型参数为：α=41.329 4 μm/V，β1=33 V-1，β2=-17.959 3 V-1，β3=-5.642 7V-1，β4=-13.079 1 V-1，β5=16.631 1 V-1，β6=-6.707 2 V-1，n=1，d=90.613 3 μm/V，建模的RMSE和RE分别为0.407 1 μm和0.014 5。

2) ARX模型辨识。辨识得到广义Bouc-Wen模型后，采用MATLAB系统辨识工具箱中系统辨识输入信号函数idinput(·)生成包含0～100 Hz频率特性信息的正弦扫描信号u(t)来激励压电陶瓷作动器，采集得到作动器输出y(t)。由输入的正弦扫描信号u(t)，基于辨识得到的广义Bouc-Wen模型，估计出中间变量x(t)，最后由ARX模型的输入、输出数据x(t),y(t)辨识出线性动态部分。

采用最小二乘法辨识得到的ARX模型为

(8)

2.2 模型检验

为了验证所建Hammerstein模型的有效性，对压电陶瓷作动器输入频率为1～100 Hz的单一频率和复合频率的正弦电压信号，测得压电陶瓷作动器的输出数据，与相同输入下所建率相关Hammerstein模型的输出数据相比较，通过RMSE和RE来检验模型的拟合程度。作动器实际输出与模型输出迟滞曲线如图3所示，图中，10/30/50/70/90 Hz和10/20/…/100 Hz均为复合频率。 表1为不同频率信号下的建模误差。

图3 模型检验

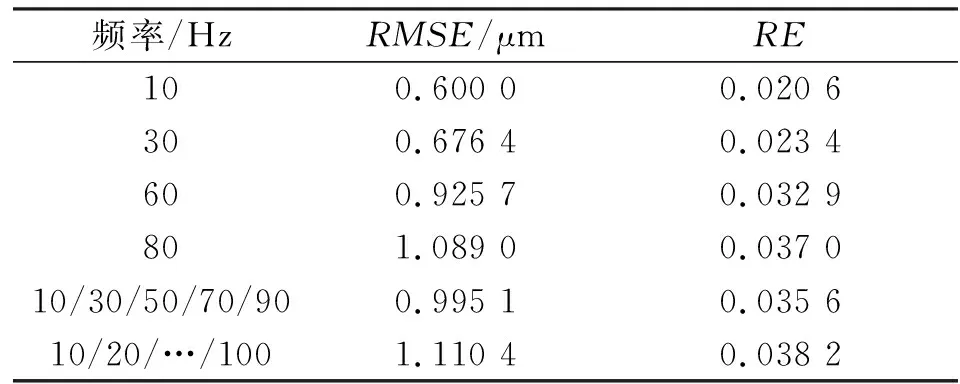
频率/HzRMSE/μmRE100.600 00.020 6300.676 40.023 4600.925 70.032 9801.089 00.037 010/30/50/70/900.995 10.035 610/20/…/1001.110 40.038 2

由图3和表1可知，所建Hammerstein模型可以有效地描述1～100 Hz内的单一频率及复合频率下的迟滞曲线。

3 控制器设计

关于压电陶瓷作动器控制器的设计，本文在所建率相关Hammerstein模型的基础上，设计了内模控制器。内模控制器是基于过程数学模型的新型控制策略，结构简单，控制性能好，实验过程中所需调节参数少，与PID控制器需要调节3个参数相比，内模控制器只需调节1个滤波器参数，设计更简便，更易于应用到工程实践中。

3.1 基于Hammerstein模型的内模控制器设计

得到Hammerstein模型后，首先求得其逆模型，再设计一个基于广义Bouc-Wen的Hammerstein模型的内模控制器，如图4所示。图中，M(·)，Q(·)和F(·)分别为辨识模型、内模控制器和滤波器，r为参考输入信号，y为压电陶瓷作动器的输出。

图4 基于Hammerstein模型的内模控制器原理图

3.2 Hammerstein迟滞逆模型

基于广义Bouc-Wen的Hammerstein模型由静态迟滞部分N(·)和线性动态部分G(z)串联组成(见图4中的M(·))，其逆模型也分别由N-1(·)和W(z)两部分串联组成。由3.1节辨识出静态迟滞广义Bouc-Wen模型后，不需要额外的计算便可得到其逆模型，这也是建立基于广义Bouc-Wen的Hammerstein模型来描述压电陶瓷作动器率相关迟滞非线性的优势之一。下面分别来求取两部分的逆模型。

图5 迟滞补偿原理

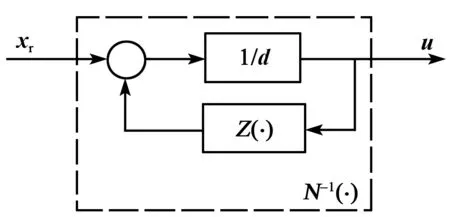
图6 迟滞补偿结构

对于线性ARX模型部分G(z)的逆模型W(z)可直接获得，即

(9)

W(z)比G-1(z)滞后1/z，但因为采样频率为10 kHz，所以W(z)和G-1(z)非常接近。

3.3 滤波器设计

模型存在误差时，有可能导致闭环系统不稳定，为了使系统具有足够的鲁棒性，在反馈通道中加入滤波器F(·)，通过调整滤波器的结构和参数来稳定系统，并有效地抑制输出振荡，获得预期的动态特性和鲁棒性[16]。

实际控制中，滤波器的选择为

(9)

式中αF(0 <αF< 1)和N分别为滤波器系数和阶数。

4 实时跟踪控制实验

4.1 实验系统构建

压电陶瓷作动器的数据采集实验及跟踪控制实验设备如图7所示。实验采样频率为10 kHz。实验设备包括：压电陶瓷作动器、功率放大器、电涡流传感器(分辨率为8 mV/μm)、控制系统dSPACE DS1103。信号由Simulink仿真图下载到dSPACE系统中，经过D/A转换后作用于功率放大器，进而驱动压电陶瓷作动器，电涡流传感器将采集到的作动器输出位移由A/D转换后再反馈到dSPACE系统中。

图7 实验设备

4.2 跟踪控制实验结果

基于第3节设计的内模控制器，选择滤波器F(·)的N=1，在线整定得到αF=0.03。实时跟踪幅值为20 μm，1～100 Hz内的单频率信号和复合频率信号。图8为不同单频率及复合频率(10/30/50/70/90 Hz和10/20/…/100 Hz)时的参考输入和作动器的实际输出曲线。表2为参考输入与作动器实际输出之间的RMSE和RE。

图8 单一频率及复合频率跟踪控制曲线

频率/HzRMSE/μmRE100.682 00.027 8301.446 40.059 6601.985 00.080 9802.087 10.085 210/30/50/70/901.466 00.067 310/20/…/1001.035 40.049 7

由图8及表2可知，在提出的内模控制策略下，压电陶瓷作动器不仅可以很好地跟踪1～100 Hz内的单频率信号，对复合频率信号也能实现良好的跟踪。

5 结束语

针对压电陶瓷作动器的率相关迟滞特性，本文提出了基于广义Bouc-Wen的Hammerstein模型，由广义Bouc-Wen模型表示静态迟滞部分，ARX模型表示线性动态部分。对1～100 Hz内的单一频率信号及复合频率信号均具有良好的泛化能力。在所建Hammerstein模型的基础上，设计了内模控制策略。不仅设计简单，控制参数少，且跟踪性能好，鲁棒性强。对幅值为20 μm，1～100 Hz内的单频率信号和复合频率信号，均能实现良好的跟踪控制效果，具有工程应用价值。