十字型结构声子晶体带隙及等效模型研究

贺子厚，赵静波，姚 宏，蒋娟娜，张 帅

(空军工程大学 研究生院，陕西 西安 710051)

0 引言

随着科学技术的发展，在日常生活中、航空航天等高精尖领域内，噪声的影响得到人们的关注，强烈的噪声会严重影响装备的性能[1]，会破坏人类工作和生活的舒适性，降低生活品质，危害人类的健康。因此对隔声材料的需求越来越高，人们不仅要求隔声材料的隔声性能要好，还要求其质量小，体积小。对于高频噪声，传统的隔声材料的吸收已很好，但因质量作用定律的限制，对于大量存在的低频噪声，传统隔声材料难以有效地吸收与隔离。近年来出现的声学超材料有望从根本上满足隔离低频噪声的需求。

声子晶体的概念类比于光子晶体提出。1993年，Kushwaha等[2]在铝/镍为材料的声子晶体中获得了剪切波完全带隙，首次提出了声子晶体的概念。1995年，R Martinez-Sala等[3]使用现代化手段测试了马德里一座历史雕塑“流动的旋律”的声学特性，第一次观测到声带隙的存在。2000年以前，所研究的声子晶体大多属于布喇格(Bragg)散射机理，其带隙频率对应的弹性波波长与其晶格常数相当。2000年，刘正猷等[4]首次提出了局域共振型声子晶体，通过对单元结构进行特殊的设计，实现波与单元结构的共振，抑制波的传播。结果表明，该声子晶体的带隙频率所对应的波长远大于晶格尺寸，达到了小尺寸控制大波长的目的。Kin等[5]根据局域共振机理设计出一种声子晶体结构，获得了200～500 Hz的低频带隙。Li等[6]发现在局域共振型声子晶体研究中出现了负的等效质量密度和负的等效体积模量。Yang等[7]首次发现，薄膜型局域共振声子晶体在50～1 000 Hz可以产生带隙，并具有良好的隔声特性。Mei等[8]和Lai等[9]设计了薄膜局域共振型超材料，解决了低频降噪减震的控制问题。温激鸿等[10]将声子晶体结构等效为“质量块-弹簧”系统，使得局域共振机理更易被人理解。后来还有人对声子晶体的结构进行了优化和创新，从而获得了更宽、更低的带隙[11-19]。

本文提出了一种十字型局域共振声子晶体，结果发现在频率30～197 Hz具有一个完全带隙，并对带隙上、下界频率振动模态建立了“弹簧-振子”等效模型。通过调节局域共振单元的结构参数得出影响带隙起始频率与截止频率的主要因素，同时验证了等效模型的合理性，从而可以有针对性地对共振结构进行优化设计。

1 声子晶体单元模型

图1为十字型声子晶体结构单元模型和第一布里渊(Brillouin)区。声子晶体单元结构是由金属芯体、带状包覆层、环氧树脂基体组成，即由4条带状包覆层连接散射体与环氧树脂基体，其中空白处为空气。表1为对应声子晶体结构参数[10]。

图1 声子晶体结构

a/mmb/mmd/mmr/mm1.00.521.06.0

目前计算弹性波带隙的方法有平面波展开法、集中质量法、有限元展开法等。其中，有限元法概念清晰浅显，适用性强，收敛性好，本文采用该方法来计算带隙。已知理想的声子晶体满足Block定理，故可通过研究单个原胞在周期性边界条件下的本征场问题来得到结构的本征频率。这里采用有限元计算软件COMSOL Multiphysics对十字型声子晶体的带隙进行计算。

根据Block定理，一个原胞内场的空间分布具有与晶格相同的周期性，场的分布满足：

uκ(r+R)=eiκRuκ(r)

(1)

式中：κ为给定的波矢；uκ为其对应的位移。

由式(1)构造边界条件。这里在单个原胞的x，y方向设置布洛赫周期边界条件，并沿第一Brillion区路径Μ-Γ-Χ-Μ对Block波矢κ进行扫描，求解结构的固有频率。

2 结果分析

使用COMSOL有限元计算软件得到该结构的能带图，如图2所示。该结构在30.98～196.46 Hz间形成较宽的低频完全带隙；在497.56～498.20 Hz、498.47～507.78 Hz会分别形成两条较窄的完全带隙，当波矢κ处于Γ—Χ—Μ时，存在一个方向带隙，且当行波频率接近497 Hz、1 052 Hz时，方向带隙截止。当行波的频率接近晶体的共振频率时，晶体将发生共振，与行波发生耦合作用，将行波的大部分能量局域化，使行波不再传播，从而产生禁带，实现声波的屏蔽(见图2灰色部分)。

图2 声子晶体能带结构

为进一步说明该带隙的形成机理，对振动模态进行分析。选取第一布里渊区的A、B、B2、C、D1、D2点进行振动模态分析，其中A点处于最下方，B1点处于次下方，B2点位于二者之上，D2处于最上，D1处于其下，振动模态如图3所示。

图3 相应共振频率下的振动模态

1) A点振动模态对应于散射体连同带状包覆层朝相同方向旋转的旋转共振模式，带状包覆层发生扭转剪切变形，仅对基体产生扭矩作用，而未产生x或y方向的合力。基体中的长行波难以与该共振模式发生相互耦合，因此未能导致局域共振带隙的产生。

2) B1、B2点处于带隙的起始频率，表现为金属芯体的平动振动，可以等效为“质量-弹簧”模型，其振子为散射体，固定端为基体，弹簧为带状包覆层。此共振模态与基体中传播的长行波产生耦合作用，相邻原胞以相同频率、相反相位的模式振动，使原胞的外框静止，整体系统处于动态平衡状态，行波的能量被局域化，从而导致了带隙的产生。

3) C点为基体的平移共振模式，当外部激励频率接近共振单元的固有频率时，局域共振模态被激发，此时，金属芯体与基体被类似于弹簧的带状包覆层连接，二者振动相位相反。声子晶体中的所有原胞同相位振动，使弹性波得以继续传播，故带隙在此处截止。

4) D1，D2点金属芯体和环氧树脂基体都处于静止状态，主要是橡胶带状包覆层的横向振动。

3 等效模型的建立

由第2节模态分析可知，十字型局域共振声子晶体的起始频率取决于散射体平动振动的谐振频率，可将其等效为“弹簧-振子”系统来估算其带隙的起始频率，如图4(a)所示。在带隙的起始频率处，等效振子质量Me、弹簧等效刚度ke组成单自由度系统发生共振。设单个金属芯体质量为mcore，单个周期内基体质量为mhost，有

(2)

式中：ρcore为金属芯体密度；rcore为圆柱形金属芯体的半径；ρhost为基体的密度；D1、D2分别为基体外框和内框的长度。

图4 声子晶体简化模型

在计算带隙的起始频率时，由于金属芯体质量远大于带状包覆层质量，故此Me可以等效为金属芯体的质量mcore。在计算等效弹簧刚度时，在金属芯体振动方向的带状包覆层发生压缩/拉伸形变，由于带状包覆层呈长条状，故可忽略带状包覆层的剪切模量G，将其弹性模量k等效为杨氏模量E；同时，垂直于金属芯体振动方向的带状包覆层发生剪切形变，同样由于其呈长条状，故可以忽略带状包覆层的E，将其弹性模量等效为G。因为金属芯体的直径远大于带状包覆层的宽度，所以可将带状包覆层看为长方形，其长度J为

(3)

等效弹簧相当于4条带状包覆层串联而成，故

(4)

式中S为带状包覆层的横截面积。在带隙截止频率处，橡胶包覆层类似于弹簧，连接基体与金属芯体，二者振动相位相反，可用图4(b)来描述这一共振模式。其中，M1为单个金属芯体的等效质量块，M2为基体的等效质量块。在带隙的截止频率处，质点M1、M2在弹簧的连接下，以相对振动方式发生共振，弹簧上虚线所示位置静止不动，即静点。

在计算带隙的截止频率时，由于包覆层的等效质量相对于基体而言并非小到可以忽略不计，故在计算截止频率时，需考虑包覆层质量。由模态分析可知，垂直于振动方向的包覆层大致随基体一起运动，因此，该部分质量mB应归入基体等效质量中，而振动方向上的橡胶包覆层质量mA应当按照静点距两质点的比例分配，即为

(5)

求解式(5)可得

(6)

显然，截止频率时等效弹簧的刚度应与起始频率时等效弹簧的刚度相同。带隙的起始频率(f1)与截止频率(f2)分别为

(7)

(8)

4 结构参数与材料参数对带隙的影响

为进一步探究该结构参数与材料参数对带隙的影响，这里分别单独改变结构中金属芯体的密度、填充率、带状包覆层的弹性模量，带状包覆层的宽度及基体的密度等参数，观察结构带隙的变化，同时使用简化模型对结构的带隙进行估算，以验证简化模型的合理性。所用材料参数如表2所示。

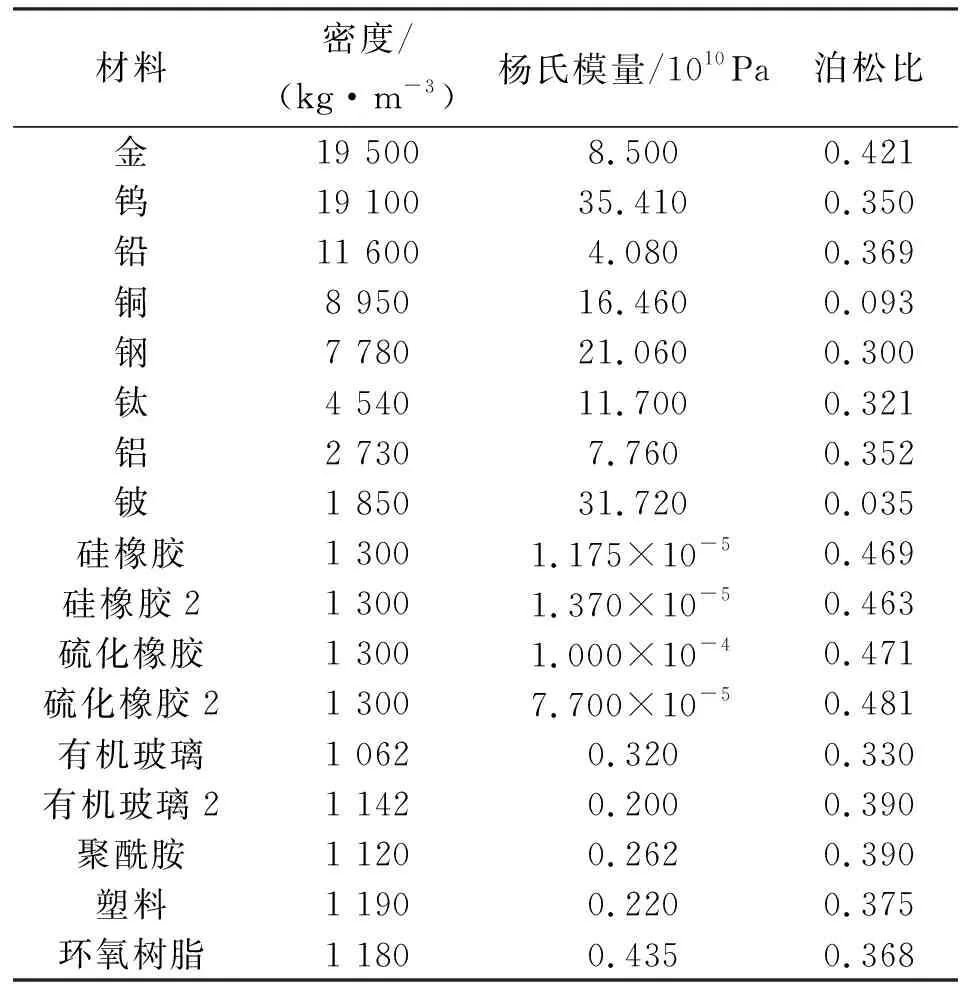
表2 材料参数

4.1 基体密度对带隙的影响

图5 基体密度对带隙的影响

4.2 金属芯体密度对带隙的影响

图6为带隙随金属芯体材料密度的变化。由图可见，随着金属芯体密度的增加，带隙的起始频率与截止频率都出现不同程度的下降，且起始频率的下降幅度大，故此使带隙变宽。这是因为相较于带状包覆层和基体而言，金属芯体的质量较大，当金属芯体的密度变化时，带隙起始频率和截止频率处模型的等效质量都会出现显著的变化。故可得金属芯体的密度对带隙的起始频率和截止频率都会产生影响，且随着金属芯体密度的增大，带隙也会逐渐变宽。

图6 金属芯体密度对带隙的影响

4.3 带状包覆层宽度对带隙的影响

本结构的一个显著特征是包覆层由两对互相垂直的带状弹性介质组成。图7为带隙随带状包覆层宽度的变化。由图可知，随着带状包覆层宽度的增加，带隙的起始频率和截止频率都出现升高，但截止频率随带状包覆层升高快，这导致带隙变宽。这是由于带状包覆层变宽会使系统的等效刚度变大，从而导致共振频率上升。由此可得，带状包覆层的变宽会使带隙的起始频率和截止频率都上升，并使带隙变宽，这是十字型包覆层声子晶体带隙的特点之一。由图7可知，随着带状包覆层宽度的增加，简化模型产生误差越来越大，这是因为结构中带状包覆层呈细长状，故简化模型忽略了振动方向纵向带状包覆层的剪切模量，及振动方向横向带状包覆层的杨氏模量，而当带状包覆层变得越来越宽，此二者的影响则会越来越大，故误差越来越大。

图7 带状包覆层宽度对带隙的影响

4.4 填充率对带隙的影响

填充率是散射体在声子晶体中所占体积比(对于二维声子晶体即面积比)。在研究过程中，常通过改变散射体的大小或改变晶格常数这两种方式来改变填充率。这里采取改变散射体大小的方式，对声子晶体带隙随填充率改变的变化情况进行研究，得到的结果如图8所示。由图可见，随着填充率的增加，带隙的截止频率增大，同时起始频率出现微小的先下降后上升的趋势，简化模型的趋势与此相同。填充率增大，带隙变宽，这与以往的研究相印证。

图8 填充率对带隙的影响

4.5 包覆层弹性模量对带隙的影响

图9 包覆层弹性模量对带隙的影响

包覆层是连接金属芯体和基体的重要介质，因此，研究带隙随包覆层弹性模量的变化尤为重要。图9为带隙随着包覆层弹性模量变化情况。由图可见，随着包覆层弹性模量的增大，带隙的截止频率迅速增大，带隙的起始频率缓慢增大，带隙的带宽也随之增大。

简化模型的估计频率(虚线)和实际值(实线)基本吻合，说明该等效模型合理。

从上述计算结果中可以看出，通过调节晶胞的结构参数与材料参数可实现对结构带隙的调控。由此可对带隙进行优化。但是，在此结构中金属芯体为圆型，基体为正方形，晶胞的大小也有限制，故此填充率与带状包覆层的宽度等结构参数只能有限增加；同时，对于材料的选择也是有限的。在实际中，材料强度等因素也会对结构的设计产生限制。综上所述，在此结构框架下，通过调节结构参数与材料参数对带隙进行的优化是有限度的。

5 结构的反射系数与透射系数

建立晶胞组成结构如图10所示，其中金属芯体材质为金，包覆层材质为硅橡胶，基体材质为环氧树脂。使用comsol有限元计算软件计算7层晶体结构的反射系数与透射系数。

图10 3×7晶体模型

分别计算此结构水平方向的反射系数与透射系数。其中，透射系数随入射声波频率的变化如图11所示。

图11 透射系数

由图11可见，此结构在中低频段有较低的透射系数，但在500 Hz、1 kHz附近出现了两个较大的透射峰，这是因为这里设置入射波为水平的从左至右的平面波。依据图2所示，在这一方向上存在方向带隙，而在500 Hz、1 kHz附近，这一方向的方向带隙截止，故此出现透射峰。

反射系数随入射声波频率的变化如图12所示。同样也与图2相符合。

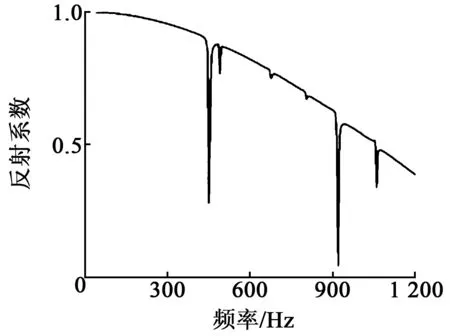
图12 反射系数

6 结论

1) 提出了一种十字型晶体结构，该结构由两对互相垂直的带状包覆层连接金属芯体和环氧树脂基体组成。在中低频率内可以获得一个完全带隙。通过调整结构参数可对带隙进行优化。

2) 对不同共振频率的模态进行分析，并将该结构简化为“弹簧-振子”模型，推导出带隙的估算公式。通过对结构参数进行改变(填充率、弹性模量和密度等)，可以调节带隙的上、下限和带隙的宽度，即减小基体的密度，增加芯体密度和填充率，增加带状包覆层的弹性模量，可进一步拓宽带隙，同时验证了简化模型的合理性

3) 计算了模型的透射系数与反射系数，结果发现，此结构在中低频段有良好的隔声性能，透射系数与反射系数随入射波频率变化的趋势与带隙图相符。

4) 这种结构的设计为获得弹性波在中低频率带隙提供了理论依据。