下击暴流作用下坡地风场特性研究

方智远， 汪之松,2， 李正良,2

(1.重庆大学 土木工程学院，重庆 400045； 2.重庆大学 山地城镇建设与新技术教育部重点试验室，重庆 400045)

下击暴流是雷暴天气中下沉气流猛烈冲击地面并沿地面扩散而引起的近地面短时强风的灾害现象。该强风现象在国内外造成了大量工程结构物的破坏，其对于输电塔结构的破坏则更为严重和频繁。实际气象资料[1]表明：由于山地和高原地区具备易于形成雷暴的天气条件，下击暴流在我国的分布呈现出山地多于平原的特征。目前国内外对于下击暴流的研究多集中于平地地形，很少考虑山坡、丘陵等地形因素对风场的影响。以往针对大气边界层风场的研究[2-9]表明：地形因素对于风场具有很大影响，其对于平均风速及近地面的湍流强度都会产生显著的加速效应，荷载规范[10]中也针对不同地形给出了相应的修正公式。

近年来，大量科研工作者通过现场实测、理论推导、物理试验以及数值模拟等方法对下击暴流开展研究，并有学者提出了下击暴流径向和竖向风剖面的解析和经验模型[11-16]，这些模型仅针对平地，未考虑地形因素对于风场的影响。Wood等[17]通过冲击射流试验及二维稳态数值模拟，考察了坡度为0.5的坡地地形风场，得出坡顶最大加速因子等于1.0加上坡度值的结论。Mason等[18]对二维坡地、三角形山体及钟型山体地形风场进行了数值模拟，发现下击暴流风场的地形加速效应比大气边界层风场小约30%。Mason等[19-21]采用简化的非稳态雷诺平均求解方法(Unsteady Reynolds Average Navier-Storkes，URANS)，通过二维平面模型研究了山丘和坡地地形对于下击暴流风场的影响，发现地形对于风速具有加速效应。汪之松等[22]采用物理试验和数值模拟的方法，研究了稳态下击暴流风场中高层建筑风荷载随坡地坡度的变化规律，但未对坡地风场结构进行细致研究。

以往对于地形影响的下击暴流风场特性的研究较少，且考虑到计算成本，多采用二维的稳态计算或简化的非稳态的URANS方法来进行计算，不能很好地捕捉风场的瞬态特征，尤其是对于结构风工程较为关注的近地面湍流特征，URANS方法模拟得到的结果则更加具有局限性。以往考虑地形影响的下击暴流风场研究均重点考察了平均风速，对于输电塔等高耸结构风振响应具有较大影响的脉动风速特性则均未涉及。

本文通过平地及三个不同坡度坡地模型的冲击射流物理试验，结合大涡模拟(Large eddy Simulation， LES)研究了坡地地形对于下击暴流风场的影响，给出了坡地地形下击暴流流场的变化规律、瞬态风速特征以及坡地坡度对于平均风特性和脉动风速均方根的影响规律。

1 冲击射流物理试验概况

物理试验在浙江大学的下击暴流风洞试验室进行，试验装置如图1所示。

图1 冲击射流试验装置Fig.1 Impinging jet instrument

冲击射流装置喷口直径Djet=600 mm，喷口到底板距离H=1 200 mm，H/D=2； 出流速度Vjet=12 m/s，几何缩尺比1∶1 000。考虑了平地和坡地两类地形，坡地地形试验工况示意图，如图2所示。R为坡地檐口到下沉气流冲击地面中心的径向距离；h为坡地高度；L为起坡位置到坡顶檐口的径向距离。以往对于下击暴流平地风场的研究表明：近地面水平风速极大值一般分布在R=1.0Djet～1.5Djet内，本文以此径向范围作为坡体所在位置进行典型坡地风场特性研究。

图2 坡地地形试验工况示意图Fig.2 Definition of terms for slope topography

坡地地形参数工况，如表1所示。用r表示地面任意位置到冲击射流中心的径向距离。试验分别测试了起坡位置，坡中位置，檐口位置(r=1.5Djet)、以及檐口后方2h位置离地不同高度处的水平风速。

表1 坡地地形模型参数

为了深入了解冲击射流在近壁区的风场特性，试验中测点布置沿高度方向采用下密上疏的排布方式，每个径向位置沿高度方向共布置15个测点，测点高度范围为10～180 mm。风速采用热线风速仪进行采集，每个测点采集风场稳定后的风速时程。

2 冲击射流数值模拟概况

用计算流体动力学方法(Computation Fluid Dynamics， CFD)软件Fluent 14.5来模拟不可压缩的下击暴流流场。为了和风洞试验进行对比，CFD数值模拟采用了与试验同比例的三维缩尺模型。其数值模型尺寸、射流参数均与物理试验模型保持一致，冲击射流计算域喷口直径Djet=600 mm，喷口到底板距离H=1 200 mm，出流速度Vjet=12 m/s，几何缩尺比1∶1 000，相应的时间缩尺为(D/Vjet)Present model/(D/Vjet)Equivalent model=3∶1 000[23]，足尺中生命周期1 000 s相当于数值模型中的3 s。平地和坡地地形计算域剖面图，如图3所示。

图3 计算域的剖面示意图Fig.3 Sectional diagram of the computational domain

本文数值模型利用LES对风场进行瞬态模拟，时间步长取0.001 s，整个计算周期为2 s，利用监测点采集完整计算周期的风速时程。为了得到更精确的数值模拟结果，本文的CFD模拟前处理采用ICEM对计算

域进行结构化网格划分，在冲击射流中心区域采用双层O型网格。在近壁面区域，采用增强壁面处理的近壁面模型来修正LES模型，以模拟近壁区的复杂流动。近壁面首层网格至壁面的距离Δy要满足无量纲距离

(1)

式中： △y为首层网格至壁面距离，m；v为空气的运动黏性系数， m2/s；τω为壁面切应力，Pa；ρ为空气密度， kg/m3。模型第一层距壁面网格距离为△y=2×10-5，使得数值模拟结果的y+<1，满足增强壁面处理方法的要求。

3 结果分析及讨论

3.1 速度云图和矢量场

以坡地模型Edx1(h/L=0.5)为例，采用冲击射流模型对下击暴流进行模拟，坡地地形条件下冲击射流形成、下沉与扩散过程的速度云图，如图4所示，重点考察了下沉气流撞击地面后沿径向发展并翻越山坡的过程，如图4(b)～图4(h)所示。

图4 下击暴流形成、下沉与扩散过程的速度云图Fig.4 The velocity contour and vector plot of downburst in different times

从图4可知，当t=0.15 s时(见图4(a))速度入口形成下沉气流并准备冲击地面，由于下沉气流与周围气体之间的拖拽卷吸作用，下沉气流前端形成了环形涡流，此时风场还未受到坡地地形的影响；当t=0.25 s时(见图4(b))，下沉气流刚刚冲击地面并沿径向发展，受地面剪切作用，沿径向发展的气流前端形成新的环形涡流，环涡处产生风速的极大值。在有坡一侧，气流开始爬坡；当t=0.3 s时(见图4(c))，环涡结构到达坡顶檐口位置，由于受到坡地地形的影响，环涡结构在翻越山坡的过程中被整体抬升，其极值风速也得到增强；当t=0.35 s时(见图4(d))，先前产生的环涡由于惯性作用而继续向斜上方运动，其体积增大而极值风速有所减小；当t=0.4～0.6 s时(见图4(e)～图4(h))，先前产生的环涡结构受惯性作用而继续发展，逐渐与近地面的气流脱离并最终消散，后续的近地面气流越过山坡，并在坡顶檐口位置附近产生明显的加速效应；当t=0.9 s(见图4(i))和t=1.2 s(见图4(j))时，风场结构已基本稳定，可以看出，在稳定阶段，风场的极值风速基本出现在山坡坡顶檐口位置附近，檐口后方风速整体较小。

冲击射流冲击地面并翻越斜坡前后四个时刻的瞬时风速矢量场变化过程，如图5所示。从图5可知，坡地的存在改变了风场的流向，气流经过山坡后，风速的竖向分量得到增强，特别是经过坡地的第一个环涡，由于坡后气流较弱，爬坡气流到达坡顶檐口后主要受惯性作用影响，故仍主要沿坡度方向运动，其风速的竖向分量明显；当风场进入稳定阶段后，如图5(d)所示。沿坡上升的气流受到坡顶后方水平气流黏滞作用的影响，在到达坡顶檐口位置时其风速方向趋于水平，但较平地风场相比，在贴近地面处仍存在较大的竖向风速。以往对于下击暴流平地风场的研究，其近地面竖向风速相对较小，主要关注水平风速，而坡地地形下，受地形的影响，檐口位置在风暴发展的早期存在较为明显的竖向风速。

图5 下击暴流冲击地面前后的矢量场Fig.5 The vector plot of downburst impacting the ground

3.2 瞬态风速特征

图6给出了坡地和平地地形下冲击射流发展过程中r=1.5Djet径向位置处不同时刻水平风速的竖直风剖面。由于地形改变了气流的运动方向，致使同一时刻平地和坡地的水平风速剖面存在较大差别，但两类地形水平风速的竖直风剖面整体均呈现下大上小的分布规律，极值风速出现高度均在z=0.05Djet(30 mm)附近。当t=0.15 s时，冲击射流还未撞击地面，故平地与坡地的风剖面几乎一致；当t=0.3 s时，平地水平风速大于坡地，结合图5(b)可知，此时环涡刚刚到达坡顶檐口位置，其风速中的竖向分量较大，水平分量与平地相比则略小；在其他时刻，平地风场近地面水平风速极大值基本稳定在0.8Vjet左右，而坡地风场由于受地形影响而产生加速效应，近地面水平风速极大值多数稳定在1.1Vjet附近。

图7给出了坡地和平地地形下冲击射流发展过程中r=1.5Djet径向位置处各时刻竖向风速的竖直风剖面。结果表明，坡地地形对冲击射流的竖向风速具有很大影响，其中，在t=0.3时竖向风速的增大最为显著，结合图5(b)可知，此时环涡结构首次抵达坡顶檐口位置，坡后气流对风速方向影响甚小，气流主要受惯性作用支配，故竖向风速较大；而当坡顶气流有所发展后，沿坡上升的气流到达檐口后受坡后气流的黏滞作用而趋于水平向运动，在贴近地面处竖向分量较大，而随着高度的增加，檐口位置处风速的竖向分量迅速减小。

图6 不同地形径向位置r=1.5Djet处水平风速的竖直风剖面Fig.6 Vertical profiles of radial velocity of flat and slope topography at r=1.5Djet in different terrain

3.3 坡地地形下冲击射流的平均风加速效应

在大气边界层风中，考察地形对于风场的影响，常通过引入加速因子Mt来进行研究。对于下击暴流，这里也采取同样的方法，通过加速因子来具体分析坡地地形对于下击暴流风场的影响。Mt是由坡地与平地离地相同高度处风速之比得到的一个无量纲值，其计算公式为

(2)

图7 不同地形径向位置r=1.5Djet处竖向风速的竖直风剖面Fig.7 Vertical profiles of vertical velocity of flat and slope topography at r=1.5Djet in different terrain

式中：z为距地面高度，这里主要考察水平风速的加速效应，故u为水平风速值。u(z)topography和u(z)flat分别为坡地与平地相同高度处的水平风速。

为了对坡地加速效应进行充分论证，将试验结果及LES的时均结果进行对比分析。图8给出了平地与各坡度坡地地形在起坡位置、檐口位置、坡中位置和坡后2h位置处时均风剖面的比较。

图8 坡地与平地各径向位置风剖面对比Fig.8 Comparison of the wind profile between flat and slope topography at different radial positions

由图8可知，LES数值模拟的时均风剖面与试验风剖面取得了较好的一致，说明了采用LES方法研究坡地下击暴流风场的有效性。数值模拟与风洞试验结果均表明：与平地风场相比，除坡顶檐口位置(见图8(c))在近地面具有显著的加速效应外，起坡位置(见图8(a))、坡中位置(见图8(b))以及坡后2h位置(见图8(d))均未发现加速效应。针对坡顶檐口位置，结合图8(c)的水平风速，给出坡地地形下的加速因子，如图9所示。

从图9可知，数值模拟与物理试验结果的加速因子沿高度变化的曲线较为一致，在近地面吻合良好。坡地檐口位置处，在z=0.06Djet(36 mm，实际风场下为36 m)高度以下均具有加速效应，近地面最大加速因子达到约1.3。在研究的三种坡地地形中，随着坡度的增大，近地面加速因子略有增大，但由于本次研究的坡地地形有限，且坡度均小于30°(h/L=0.58)，故针对陡坡地形，其坡地风场加速因子的变化规律还有待进一步研究。

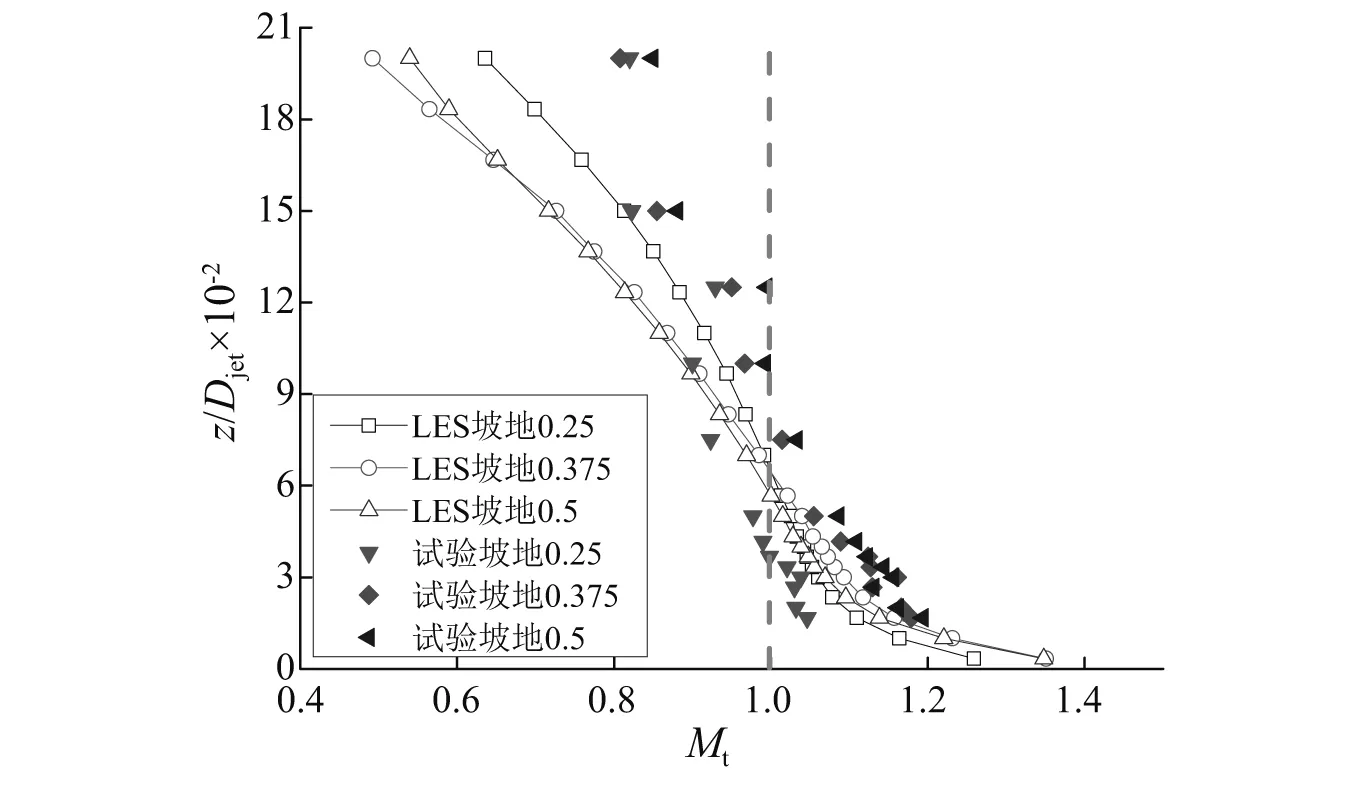
图9 数值模拟和物理试验结果加速因子对比Fig.9 Topographic multiplier profiles of numerical simulation and experimental results

3.4 冲击射流的脉动风速湍流强度特性

坡地地形下下击暴流的脉动风速特性在已有的研究中几乎是空白。在输电塔、高层建筑等的响应中，脉动响应往往远大于平均风响应，而脉动风速特性是确定脉动响应的直接因素，其重要性完全不低于山地的平均风特性。同平均风速加速因子定义类似，可以定义脉动风速的湍流强度加速因子MI为

(3)

式中：z为距地面高度；I(z)topography与I(z)flat分别为坡地和平地离地相同高度处的湍流强度。

试验中平地和坡地Edx3模型在各个径向位置脉动风速湍流强度剖面特性，如图10所示。图中实线和虚线分别为风洞试验测得的平地和坡地湍流强度值，分别对比了起坡位置(r=1.0Djet)、坡中位置(r=1.25Djet)、檐口位置(r=1.5Djet)、檐口之后2h位置处；图11所示为坡地各个位置处湍流度加速因子剖面图。从图11可知，离下沉气流冲击中心越远，湍流度越大。在r=1.0Djet～2.0Djet径向位置范围内，湍流度剖面沿高度均是先减小，后增大。平均风速大的位置，湍流度小；平均风速小的地方，湍流度大。受到坡地地形的影响，在近地面区域，坡中和檐口位置处的湍流强度相对平地增大不明显，但超过一定高度(0.02Djet)后，坡地地形湍流强度都显著增大；起坡和坡后位置相对于平地风场在近地面区域湍流强度有显著增大，超过一定高度后(0.1Djet)后坡地地形湍流强度增大不明显。上述对比说明坡地地形对冲击射流的湍流强度有显著影响。

图12所示为试验中不同坡度坡地(h/L=0.25，h/L=0.375和h/L=0.5)在檐口位置与平地的湍流强度对比，图13所示为不同坡度坡地湍流强度加速因子沿高度变化曲线。从图13可知，在近地面区域，各坡度坡地地形湍流强度相对平地增大不明显，但超过一定高度(0.02Djet)后，湍流强度显著增大，且当坡度较大时(h/L=0.5)，湍流强度增大更为明显。

图10 坡地与平地各径向位置湍流度剖面对比Fig.10 Comparison of turbulence intensity profiles between flat and slope topography at different radial positions

图11 坡地各位置湍流度加速因子对比Fig.11 Comparison of multiplier profiles between flat and slope topography at different radial positions

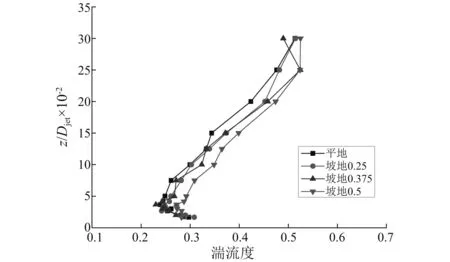
图12 不同坡度坡地与平地湍流度剖面对比Fig.12 Comparison of turbulence intensity profiles between flat and different slopes

图13 不同坡地湍流度加速因子对比Fig.13 Comparison of multiplier profiles in different slopes

4 结 论

本文通过冲击射流物理试验以及大涡数值模拟对下击暴流作用下的平地及坡地风场进行研究，给出了坡地地形对于下击暴流风场、瞬态风速特征、平均风特性以及近地面湍流强度影响的基本规律。主要结论如下：

(1) 下击暴流在坡顶檐口位置处具有显著的加速效应，且越过山坡的第一个环涡在檐口位置形成下击暴流整个生命周期中的最大风速。气流越过山坡的初期，受惯性力作用，檐口位置处风速的竖向分量较大，后期由于受到坡后气流的黏滞作用，竖向分量有所减小。

(2) 坡地的存在改变了风场的原始结构，致使檐口位置处的水平风速与竖向风速都有所增大。风场稳定后，平地风场近地面水平风速极大值约为0.8Vjet，而坡地(L/h=0.5)风场水平风速极大值多数稳定在1.1Vjet附近。竖向风速在初始环涡经过时较大，之后受坡后气流的影响而有所减弱，但与平地风场相比，在贴近地面处其竖向风速增大明显。

(3) 在近地面区域，坡地地形条件下冲击射流数值模拟和物理试验给出了一致的结论，檐口位置有加速效应，而起坡位置、坡中位置和坡后2h位置处都没有加速效应。在缓坡地形下(L/h≤0.5)，坡顶檐口位置处近地面水平风速最大加速因子达到约1.3。

(4) 试验结果表明，与平地风场相比，坡地风场近地面湍流强度增大的区域为起坡位置和坡后位置，而坡中和檐口位置在近地面湍流度相对较小，但随着高度的增加，湍流度明显增大，其变化符合平均风速大的位置，湍流度小；平均风速小的地方，湍流度大的规律。对不同坡度坡地檐口湍流度加速因子的研究则表明，缓坡地形下(L/h≤0.5)，随着坡度的增大，其湍流度有所增大，但湍流度随坡度变化的完整规律还需通过增加坡度工况来做进一步研究。