合同节水管理模型对节水管理效益分配的对比研究

鲁达明

（上海市供水管理处，上海 200081）

合同节水是由专业的第三方节水服务机构为合同签订对象提供一对一的节水服务并共享节水效益的一种新型的市场化节水机制[1]。在水资源短缺，水环境日益恶化的当下，推行合同节水不仅有利于合理开发和利用水资源，同时还能创造巨大的市场经济效益，促进社会经济的健康发展[2]。然而，由于合同节水在我国起步较晚，很多理论和实践都未成熟，在推行过程中还暴露出众多弊端，如合同节水的效益分配就是一个比较突出的问题，需要做专门的研究和探讨[3-4]。

合同节水管理要注重体制机制的建立和完善，同时还应该建立统一标准，以促进合同节水向专业化迈进[5-6]。不同的社会经济情况，需要特定的合同节水管理技术和手段，在一定程度上，由于是市场化调节，故而也存在项目的风险，即自负盈亏[7]。郭路祥等利用干系人分析和投资模式对比的方式阐述了合同节水管理投资模式的优势,寻求可以保证合同节水管理项目投资的长效性和可持续性,以及通过利益分配的模式增强投资效能的方法[8]。钟恒等以高效为例，对合同节水改造效益进行了分析，发现每月可较之前节水约40%[9]。尹庆民等则专门对合同节水管理的利益分配问题进行了研究，得出项目各参与方实际所得利益，对于利益分配机制的建立健全就有重要意义。本文则分别为采用Shapley 模型、修正的Shapley 模型以及公平熵模型三种方法对某用水企业、节水服务公司以及投资方三者的利益分配问题进行了对比分析研究，以期能为合同节水管理的推广应用提供借鉴。

1 合同节水管理主要效益分配方

节水项目主要划分为合同前准备阶段，合同实施阶段以及合同后期维护运行阶段，见图1。本文所研究的时间段为t1～t3，即从合同前至合同后。合同节水项目的参与方包括：节水服务公司，节水用户，投资者，节水技术咨询公司等相关单位，按照米切尔评分原则，以紧迫性、权利性以及合法性为评价指标对各利益相关者打分，结果见表1。从表中评分结果可以看出，从紧迫性、权力性以及合法性来讲，节水服务公司、节水企业以及投资者的评分结果均为高，这说明上述三者为合同节水管理的主要效益分配方，下文将围绕此三项进行计算分析。

图1 合同管理时间关系

2 模型简介

2.1 S hapley 模型

合作博弈论适用于合同节水管理的全过程，即认为节水服务公司、节水企业与投资者之间是合作博弈的过程。其满足两个条件，一是当没有参与者时，不会产生合作效益，二是合作产生的效益大于各方单独合作时的效益和。假设K、M 分别为各参与方集合和联盟组合，ψi 表示项目参与方I 的所得利益，那么根据Shapley 的有关定理可得：

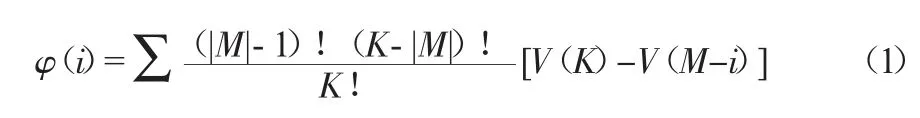
式中：|M|表示联盟的单位数；V（M-i）表示除去参与者I 后的利益；V（K）-V（M-i）表示参与者i 的边际贡献值。假设节水服务公司、节水企业与投资者分别为代表第1、2、3 参与方，那么其分配利益值即可表示为φ（1）、φ（2）、φ（3）。

2.2 修正的S hapley 模型

在传统的Shapley 模型基础上，引入对（1）成本投入、（2）节水效果以及（3）风险承担后果等的修正系数，其修正系数矩阵为：

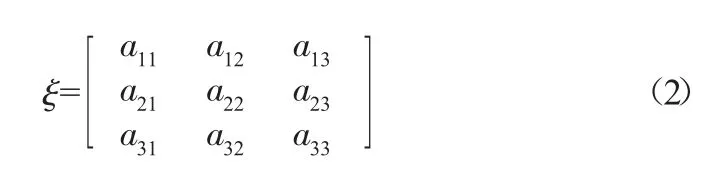
其权重矩阵为：a=|a1a2a3|T，那么由ξa 可得修正系数β，那么修正后的利益分配即可表示为：

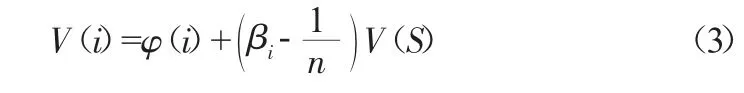
式中：V（i）表示修正后各方所得利益值，表示联盟合作总收益。

2.3 公平熵模型

假设节水总效益为A,总投入为B，那么节水效益φ=A-B，再假设节水服务公司效益分配占比为α，那么节水企业与投资者的占比则为1-α，有：

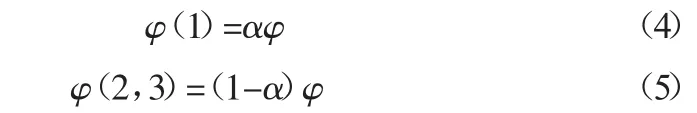
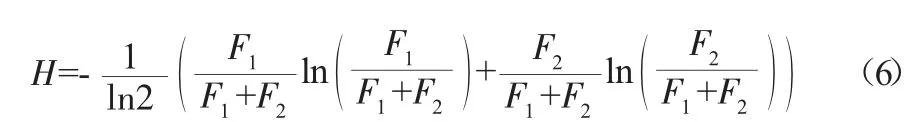
最后通过模型求解，得到：

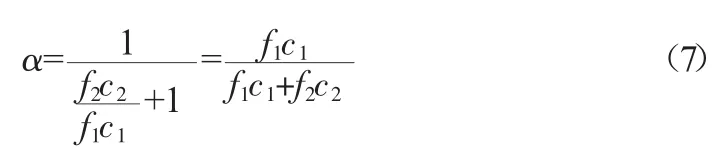
式中：f1、f2、c1、c2为计算系数且大于0，即可算出节水服务公司效益分配占比为。同理再在节水企业与投资者的节水效益值上，采用上述理论方法，分别得到节水企业与投资者的效益分配。

3 实例分析

3.1 节水项目概况

某大型国有企业分工厂（代号C），总占地面积90.2 hm2，主工厂及住宿占地面积约为50 hm2，职工人数约3200 人。由于该工厂是上世纪60 年代建立的，因此其机械设备、用水管网、生活设施等均比较老旧，经常出现跑、冒、滴、漏等现象，据统计，该工厂年均用水量约为800 万t，年缴水费约2500 万元，开展节水项目已刻不容缓。

节水项目主要由节水服务公司（代号P）牵头，其拥有目前国内比较成熟的合同节水方式，能吸引各方资源及核心技术方的参与，同时积极引导某证券投资公司（代号R）设立相关的专项技术资金，即作为投资方。节水项目概算共1500 万元，合同期为10 年，节水改造历时约4 个月，主要完成水龙头更新1.5 万余只，地下管网改造约3.7 km，，在主工程及各生活区域建立多个用水监测管理平台。合同节水改造前，其月均用水量为66.7 万t，合同节水改造后，其月均用水量仅为43.2 万t，节水效率达35%，年节约用水量达282 万t，按当地水价初步计算可节约水费1100 余万元，见图2。

图2 节水前后用水量对比

3.2 不同模型分配结果对比分析

（1）Shapley 模型。首先根据相关经验及统计数据，分别作出单独C、单独P、单独R，C+P、C+R、P+R 以及C+P+R7 种情况下的利益分配假设，见表2。从表中可以看出，当企业自行改造，与节水服务公司合作以及采用与节水服务公司及投资者合作时的受益值分别为总节水效益的30%、50%以及100%，而企业与投资者合作时仅产生50%的收益值。

表2 合作利益分配表

根据Shapley 模型原理，令：

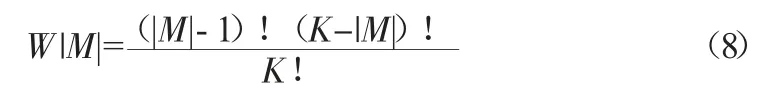
即可分别得到节水服务公司、节水企业以及投资者的节水受益分配值（文中不再一一详列）。再根据公式（1）即可分别为得到各自的收益值：

节水服务公司的收益值：

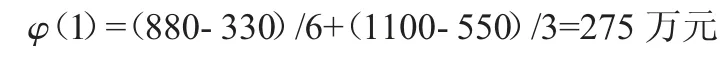
节水企业收益值：

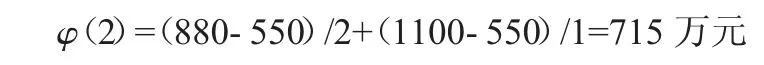
投资者收益值：

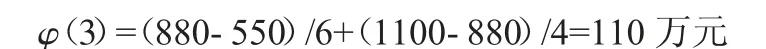
（2）修正Shapley 模型，前者已经利用Shapley 模型分别得到了三者的节水受益分配值，然后可通过专家评分，得到修正系数矩阵为：

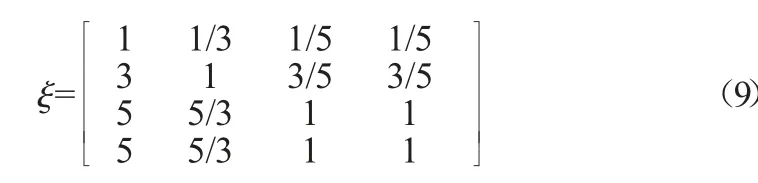
修正影响度矩阵为：a=|a1a2a3|T，那么进一步可得修正系数：

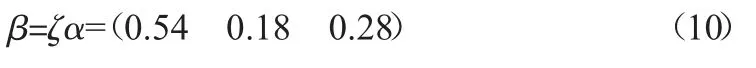
再将其带入公式（3）可得修正后的节水利益分配值分别为：

节水服务公司的收益值：

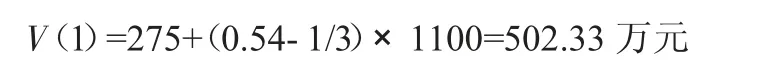
节水企业的收益值：

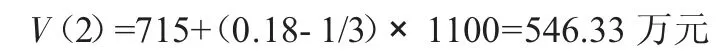
投资者的收益值：

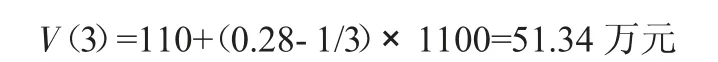
（3）公平熵模型。由于公平熵计算过程较为复杂，文中不再赘述。通过第一次迭代得到的α（1）为0.48，第二次得到的α（2）为0.52，分别代入公式（4）、（5），即可得：

节水服务公司的收益值：φ（1）=0.48×1100=528 万元

节水企业收益值：φ（2）=0.52×572=297.44 万元

投资者收益值：φ（3）=0.48×572=274.56 万元

通过对比三种模型计算得到的收益分配值，见图3，可以看出：不同的分配计算模型对于计算结果有较大的影响，Shapley模型计算得到的收益值为节水企业最大，其次为节水服务公司和投资者，表明在此计算原则下，节水企业将得到最大的效益分配；修正的Shapley 模型计算得到的收益值结果为节水服务公司和节水企业差别不大，最小的为投资者；公平熵模型得到的结果为节水服务公司最大，节水企业次之，投资者最小，说明在此原则上节水服务公司将得到最大的节水效益分配。

图3 不同模型效益分配对比

4 结论

对Shapley 模型、修正的Shapley 模型以及公平熵模型三种合同节水管理模型的分配计算原理进行了介绍，并进行实证分析，结果显示：在Shapley 模型计算原则下，节水企业将得到最大的效益分配；在修正的Shapley 模型计算原则下，节水企业和节水服务公司得到效益分配值相当；公平熵模型计算原则下，节水服务公司得到的效益分配值最大，节水企业和投资者次之。