改进遗传算法在城市多水源供水联合优化调度中的应用

李力南

(大石桥市水源水利管理处，辽宁 营口 115100)

当前，城市供水矛盾日益紧张，为满足城市供水的可持续利用，需要对城市供水多水源进行联合优化调度。对于城市供水优化调度的研究成果较多[1-5]，但这些成果往往未能实现城市供水分时段的优化调度。城市供水具有典型的分时段特征，用水高峰期，城市供水水量明显加大。改进的遗传算法可实现变量分段优化，在许多领域的优化调度中得到应用[6-10]，但在城市多水源联合优化调度中还未进行相关应用。为此，本文引入改进的遗传算法，以北方某典型干旱城市为研究实例，结合改进的遗传算法对该城市多水源进行分时段的优化调度。

1 城市多水源联合优化调度数学模型

假定供水量为变量，首先对供水量进行有机组合预测，组合方程为：

(1)

式中，At—供水量预测值，万t；Yt—组合预测的水源变量；f1t、f2t、fmt—不同预测时段的供水量，万t；k1、k2km—各时段的组合权系数；yt—t时刻的单元供水量，万t。

改进的遗传算法结合有效度对方程预测供水量进行优化调整，调整方程为：

S=E(At)(1-σ(At))

(2)

式中，S—调整后的供水量，万t；E(A(t))—预测变量系列的均值，万t；σ(A(t))—预测变量系列的方差。调整后，以变量S为约束变量，调整后的的优化模型方程为：

maxS=E(At)(1-σ((At))

(3)

式中的变量含义同式(2)中的变量含义，预测变量At与各时段组合权系数k的相关关系为：

At=kA1t+(1-k)A2t

(4)

式中，A1t—初始时段的供水水量预测值，万t；A2t—其他时段的供水水量预测值，万t。各时段组合预测均值与分段组合权系数的关系式为：

E(At)=kE(A1t)+(1-k)E(A2t)

(5)

式中，E(A1t)—初始时段的供水水量预测均值，万t；E(A2t)—其他时段的供水水量预测均值，万t。各时段组合预测方差与分段组合权系数的关系式为：

(6)

式中，σmin—预测变量系列均方差最小值；σ(A1t)—初始时段的供水水量预测均方差；k0—初始时段的组合权系数。

2 实例分析

2.1 实例概况

本文以北方某典型干旱城市为研究实例，该城市的多年地表水资源总量为2.57亿m3，供水水源主要来自流域内的地下水及外调水，日供水量均值约为2.9万t，区域内主要的供水水源为10处，此外在供水水源配有抽水泵站12处，抽水开采水井9处，各抽水井的深度为70～95m，区域供水拓扑结构如图1所示。该城市的供水时段高峰区域主要集中在06～09时以及17～22时。本文结合该城市2个供水水源，结合改进的遗传算法，对该市的供水水源进行联合优化调度，确定分时段最佳优化调度方案。

2.2 模型分时段参数设置结果

在优化前，需要对模型各分时段的参数进行设置，结合改进遗传算法的计算方法，对各时段参数进行设置，设置结果见表1。

表1 模型分时段参数设置结果

2.3 不同算法下的评价结果对比

结合不同评价指标对传统算法和改进算法下不同拓扑单元数目进行了评价，评价结果见表2。

表2 不同算法下的精度评价结果

注：*MAD表示为收敛度；MSE表示为均方误差；MAPE表示百分比误差。

从各指标的评价精度可以看出，改进的遗传算法下各拓扑单元的收敛度、均方误差以及百分比误差都叫传统算法有明显改进，这主要是因为改进的遗传算法采用有效度对各拓扑单元的结构进行优化，相比于传统算法优化收敛精度有较为明显的提高，相比于传统算法，其优化收敛精度均值提高28.7%，优化收敛精度的提高也使得改进算法下各拓扑单元的均方法误差和百分比误差得到降低。

2.4 模型验证结果分析

结合供水点及测压点监测结果对各时段模型供水压力预测值进行验证，各算法验证结果见表3—4。

从表3—4中可看出，改进算法下供水点各时段的相对误差在8.65%～12.54%之间，测压点各时段相对误差在8.23%～-14.209%之间，而传统算法下，各时段供水点预测相对误差均高于20%，在-21.05%～-34.36%之间，而测压点的误差在20.25%～38.10%之间，相比于改进算法，传统算法的误差较大，改进算法下误差明显递减。

图1 供水水源拓扑结构

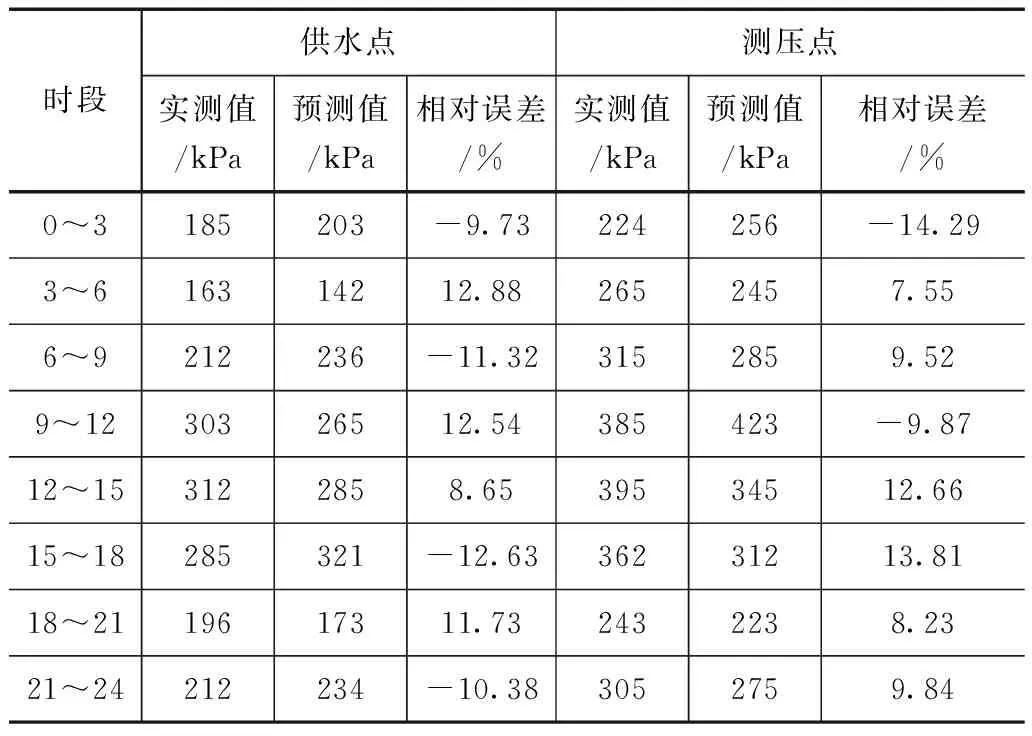
时段供水点测压点实测值/kPa预测值/kPa相对误差/%实测值/kPa预测值/kPa相对误差/%0～3185203-9.73224256-14.293～616314212.882652457.556～9212236-11.323152859.529～1230326512.54385423-9.8712～153122858.6539534512.6615～18285321-12.6336231213.8118～2119617311.732432238.2321～24212234-10.383052759.84

表4 传统算法下验证结果

2.5 优化调度方案分析结果

结合构建的多水源联合优化调度模型对区域各供水组合方案进行联合优化调度，调度结果见表5，并对比优化前后的供水方案，如图2所示。

表5 区域多水源组合联合优化调度结果

表5为各供水组合不同时段的优化调度方案，从表中可发现6#组合方式下的供水量偏少，1#组合方式下的供水量较大，而4#组合方式下的供水量较为适中。从图2中可分析出，相比于优化前，优化后各组合供水方式下供水资源效率平均可提高25%～30%，从各组合供水方式优化前后结果可看出，在用水量较低的时段，优化水量相比于优化前供水减少，而在用水高峰时期，优化水量相比于优化前增多，保障了用水高峰时段的水量。从综合比较看，推荐4#组合供水方案为区域最优的供水调度方案。

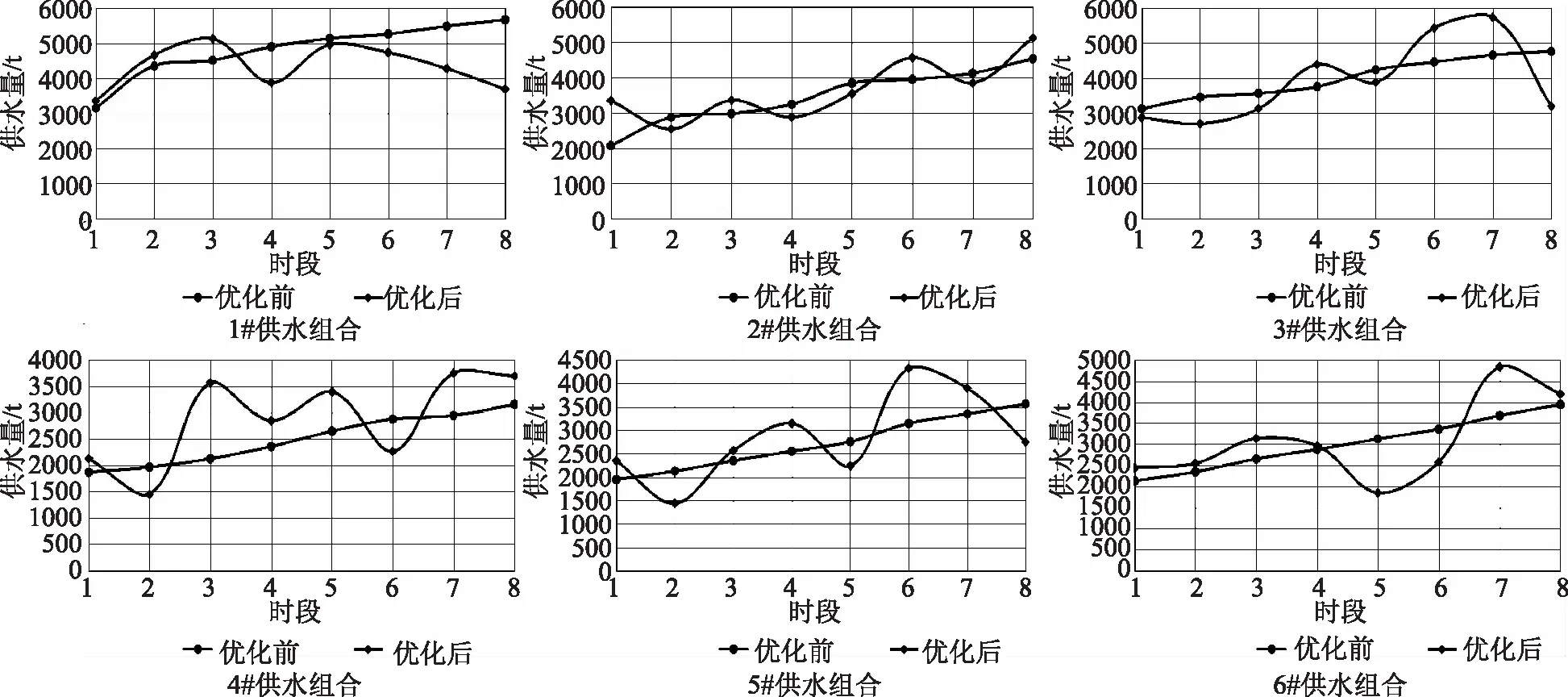
图2 不同组合供水水源优化调度前后方案对比结果

3 结语

(1)改进算法结合有效度对各供水水源拓扑单元进行结构优化，可实现分时段供水水源联合优化调度，该方法更符合供水调度的实际，在实际供水调度中更为有效。

(2)本文未对各供水水源的可供水量进行分析，在以后研究中进行供水水源联合优化调度时还需要对组合方式下可供水量进行分析，从而对优化调度方案进行调整，使得优化方案更贴合实际供水能力。