基于ANN的公路隧道火灾临界风速预测研究

梁华刚，庞丽琴，高冬梅

（长安大学 电子与控制工程学院，西安 710064）

随着我国社会经济的发展和现代化进程的加快，人们对便捷交通运输的需求日益增大，隧道作为能够穿越崇山峻岭与江河湖泊等障碍的工程建筑物，在公路建设中被大量应用。截至2017年底，全国有公路隧道16229处、15285.1 km，其中特长隧道 902处、4013.2 km， 长隧道 3841处、6599.3 km[1]。火灾作为隧道最大的安全隐患，其发生概率也呈逐年上升趋势。临界风速作为隧道火灾纵向通风排烟设计中的关键性参数，其大小直接决定了能否对隧道进行有效的排烟，因而引起国内外学者的广泛关注。

1 隧道火灾临界风速的研究现状

目前，对隧道火灾临界风速的研究主要采用模型试验方法和数值模拟方法。

在模型试验研究方面，1965年瑞士在Ofenegg隧道对多种火灾工况进行了全尺寸试验[2]；1968年Thomas通过对试验研究所得数据结果进行推导，得出火源功率的1/3次方与临界风速成正比的结论，并提出初步的临界风速计算公式[3]；随后Heselden，Danziger和Kennedy在全尺寸隧道内进行试验，对Thomas的预测公式进行验证并推导出新的临界风速半经验预测公式[4-5]。

数值模拟研究方面，20世纪70年代末帕森斯研发了模拟地铁环境火灾的计算机模拟软件；随后Cox等人将计算流体动力学CFD（computational fluid dynamics）方法应用于公路隧道的火灾研究上，并成功构建了JASMINE模型[6-7]。此外，美国的C.C.Hwang和J.C.Edwards利用 FDS（fires dynamics simulator）软件对2个尺寸不同的隧道临界风速进行模拟，并提出隧道火灾计算模型[8]。

上述研究多基于某单一影响因素，而对于多种影响因素下隧道火灾临界风速预测的研究并不多见。由于火灾过程中影响临界风速的因素非常多，且很难用现有的数学函数公式进行准确的表达。在此，以传统数值模拟方法为基础，引入BP神经网络[9]，对多种影响因素下隧道火灾临界风速的预测展开研究，借助人工神经网络特的非线性信息处理能力、自适应学习能力和联想记忆能力等，为公路隧道火灾临界风速的预测研究寻找一种新方法。

2 数值模拟

FDS是美国国家标准与技术研究所开发的一款基于场模拟的火灾模拟软件，主要利用大涡模型求解连续方程、动量方程、能量方程及压力收敛方程等，从而得到温度等参数的空间分布，并结合可视化工具SmokeView，使模拟变得形象直观。在此，采用FDS软件对多种影响因素下隧道火灾临界风速的变化规律进行模拟研究。

2.1 物理模型及相关参数设置

参照JTG D70—2004《公路隧道设计规范》中隧道横断面设计的相关规定，以高速公路设计速度为80 km/h的隧道横断面参数为依据，设计双车道公路隧道的横断面，隧道长度设置为300 m。隧道模型如图1所示。

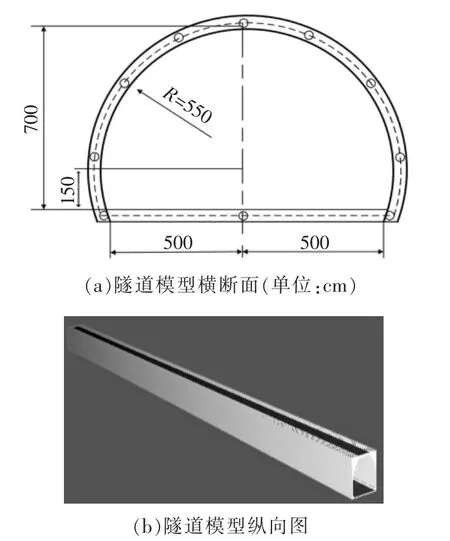
图1 隧道模型Fig.1 Tunnel model

隧道模型的左侧端设置为入口速度边界条件（fan），对隧道进行纵向通风；右侧端设置为出口边界条件（open），便于隧道向下游方向排烟。环境温度设置为20℃（即293 K）；环境压强设置为1个标准大气压即101.325 kPa；燃料采用丙烷；选取的隧道墙壁为热厚性边界（concrete）。根据计算网格的设置方法同时保证模拟精度，隧道模拟区域采用均匀网格，选取的网格尺寸为0.25 m×0.25 m×0.25 m。

文中运用所建立的隧道模型分别对火源功率、火源宽度、火源位置、阻塞比和坡度等5种影响因素下的临界风速进行数值模拟计算，共设置139组工况。

3 BP神经网络预测模型

BP神经网络，是目前人工神经网络模式中最具代表性、应用最广泛的一种模型，具有自学习、自组织、自适应和极强的非线性映射能力，其结构简单、运算能力好且结构可塑性强。故在此选取构建BP神经网络对公路隧道火灾临界风速进行预测研究。

3.1 BP神经网络预测原理

BP神经网络是一种多层前馈网络，由输入层、隐含层和输出层构成。典型的3层BP神经网络拓扑结构如图2所示。其网络结构的设计更利于从样本数据中获取更多信息，得到输入输出之间的联系，从而解决复杂的实际应用问题。

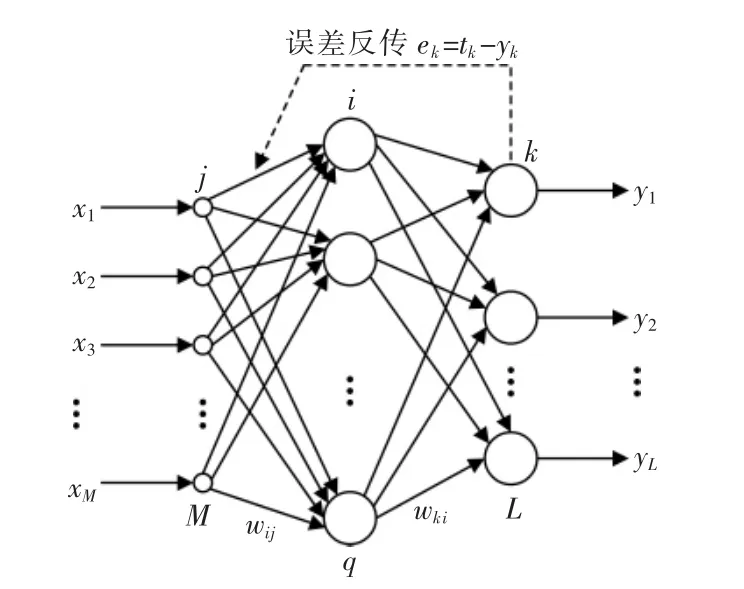
图2 典型BP神经网络模型Fig.2 Typical BP neural network model

以图2所示3层BP网络为例。设网络输入节点为xi，隐含层节点输出为yi，网络输出节点为zk，输入层与隐含层的连接权值为wij，隐含层与输出层的连接权值为wki，隐含层阈值为θj，输出层阈值为θk，输出节点的期望值为tk。

定义误差函数为

3.2 BP神经网络结构设计

该模型选取含1个隐含层的3层BP神经网络。

1）神经元数的确定 模型选取火源功率、火源宽度、火源位置、隧道阻塞比和坡度等5个因素作为输入变量，即5个输入层神经元；1个输出层神经元，为临界风速。

2）传输函数的确定 所研究的内容属于非线性问题，故选用非线性tansig函数作为传输函数。该函数具有很好的非线性映射能力。

3.3 网络训练算法优化

由于标准BP算法存在易陷入局部极小化、收敛速度慢，以及隐含层的层数与节点个数的选取缺乏理论指导等缺陷，为了提高训练速度，避免陷入局部极小点和改善其他能力，在此对比几种改进其权阈值的方法——附加动量法、拟牛顿法和LM算法。

在相同条件下，运用附加动量法、拟牛顿法和LM算法3种改进的训练算法与标准BP算法对网络进行训练对比，从而确定最优算法。4种算法对应的训练结果如图3所示。

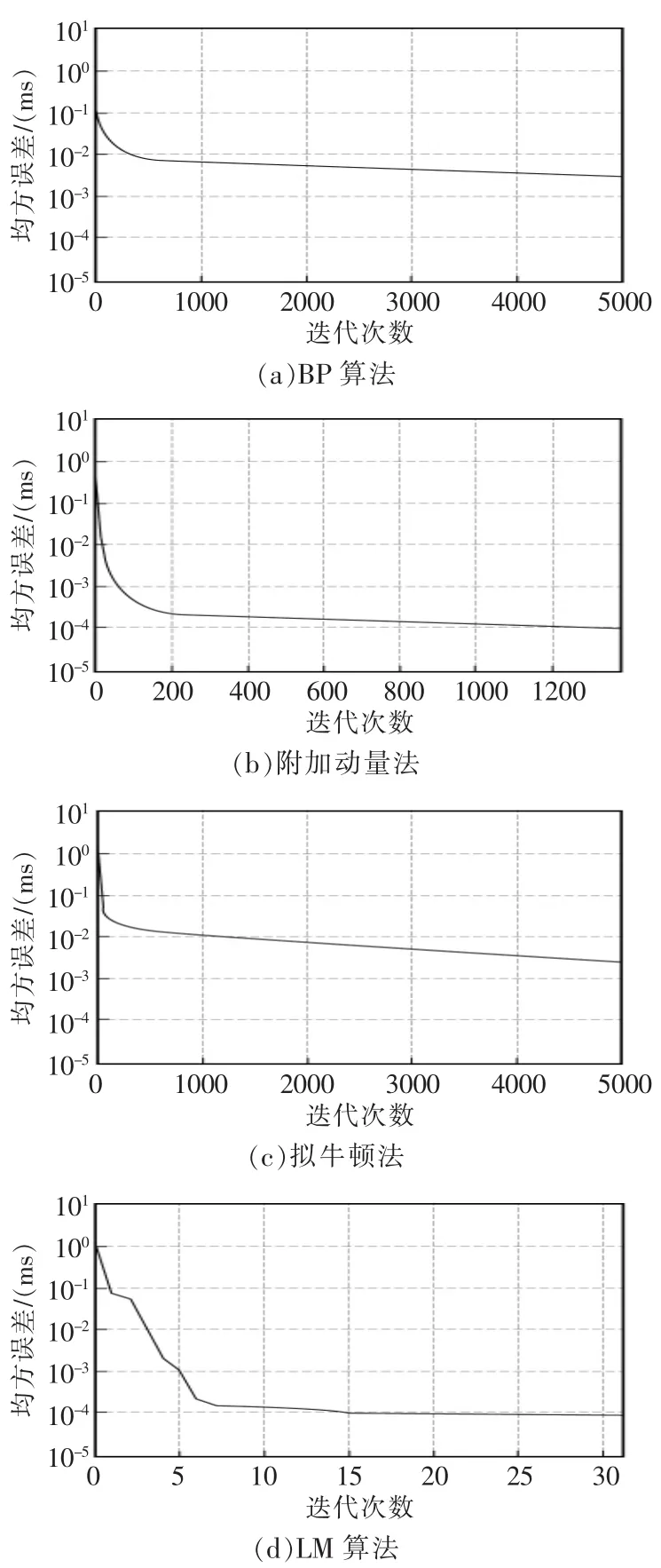
图3 不同算法的训练效果Fig.3 Training effect of different algorithms

由图可见，综合几种算法的训练效果，LM算法具有较快的收敛速度和较强的收敛能力。因此，选取LM算法作为网络的训练算法，用于改进BP神经网络模型。

4 数值模拟试验与结果分析

4.1 火源功率对临界风速的影响

为了研究火源功率对临界风速的影响，选取5，10，15，20，25，30 和 35 MW 等 7 种隧道中常见的火灾规模进行数值模拟，设置火源尺寸为2 m×2 m，位于隧道模型中心位置。在隧道拱顶布置了21个热电偶，相邻两个热电偶间距离为2 m，通过在拱顶布置热电偶来测量火源达到稳定燃烧时各测点的温度，从而验证本文模拟计算得到的临界风速的准确性。温度测点示意图如图4所示。将本文模拟结果与Wu和Bakar预测结果[10]、于年灏试验结果[11]进行对比，如图5所示。

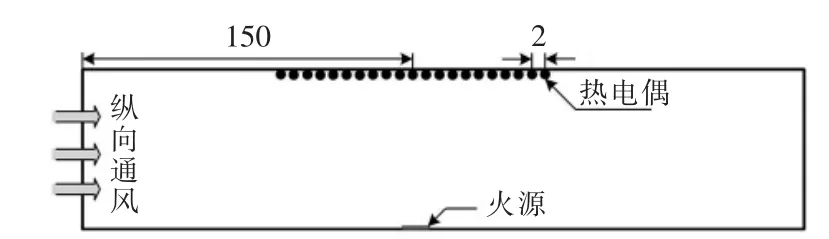
图4 温度测点位置示意图（单位：m）Fig.4 Schematic diagram of location of temperature measurement points （unit：m）

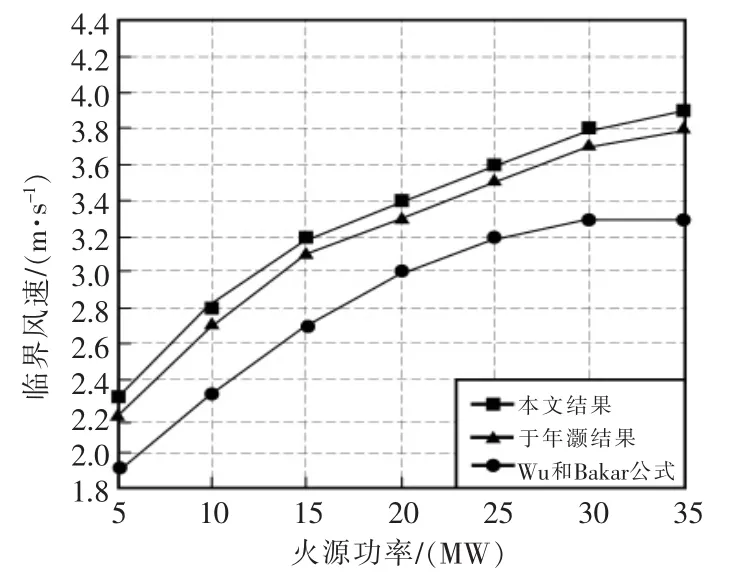
图5 临界风速与火源功率关系的对比Fig.5 Comparison of the relationship between critical wind velocity and fire source power

由图5可见，三者都较为相似，但本文模拟计算值略高于于年灏试验结果，主要由于后者采用矩形隧道横截面，在面积和隧道高度上存在差异；本文模拟计算值明显高于Wu和Bakar公式预测值，是由于后者在试验时为防止火灾烧毁隧道采取了降温处理，因此其临界风速预测值比真实值偏低。通过与两者的对比，验证了本文模拟结果的可靠性。

4.2 火源宽度对临界风速的影响

为研究火源宽度对临界风速的影响，将火源设置于隧道中心位置，保持火源长度2 m不变，仅改变火源宽度。火源宽度变化模型如图6所示，具体的工况设置和模拟结果见表1。

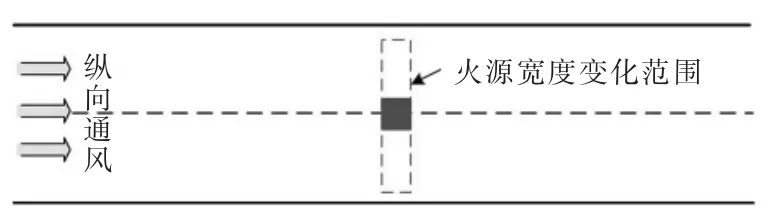
图6 火源宽度变化模型示意图Fig.6 Schematic diagram of fire source width variation model

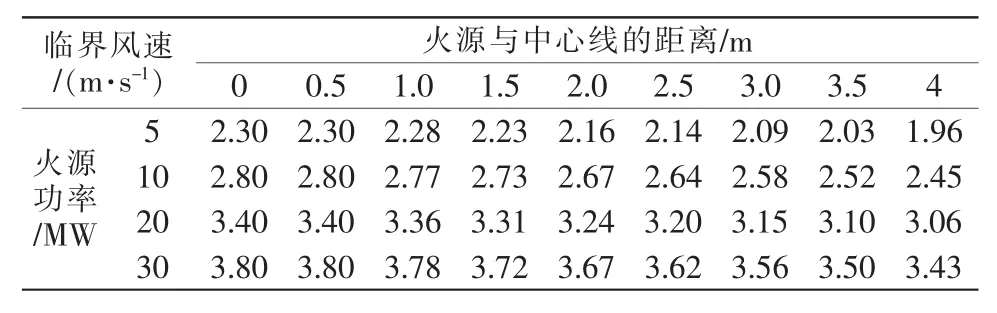
表1 不同火源宽度的模拟工况及测试结果Tab.1 Simulation conditions and test results of different fire source widths

由表1可知，当火源宽度变化时，不同火灾规模下临界风速变化趋势基本一致，临界风速均随着火源宽度的增加而不断减小，且各火灾规模下临界风速的最大值与最小值的差值约为0.92 m/s。

4.3 火源位置对临界风速的影响

通过改变火源与隧道中心线距离来研究临界风速的变化，其他参数保持不变。火源位置变化模型如图7所示，具体的工况设置和模拟结果见表2。

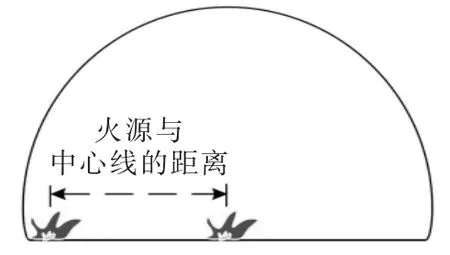
图7 火源位置变化模型示意图Fig.7 Schematic diagram of fire source position change model

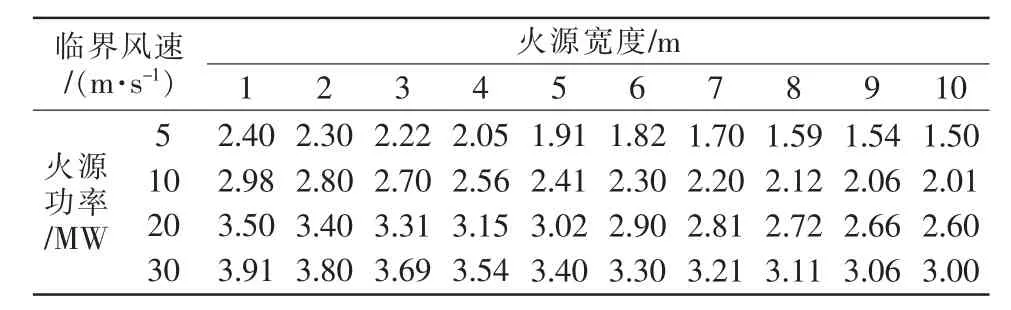
表2 不同火源位置的模拟工况及测试结果Tab.2 Simulation conditions and test results of different fire source locations

由表2可知，相同火源功率下，临界风速随火源位置的变化趋势基本一致，都是随火源与中心线距离的增大而减小。

4.4 阻塞比对临界风速的影响

通过调研，选取小轿车、面包车、卡车和货车等4种常见车辆类型，作为火源上游的阻塞车辆。每种车辆分别以2列和3列的排列方式分布于火源的上游，隧道中车辆布置情况如图8所示，具体的工况设置和模拟结果如表3所示。

定义隧道阻塞比为β，即隧道中阻塞物横断面与隧道全断面之比为

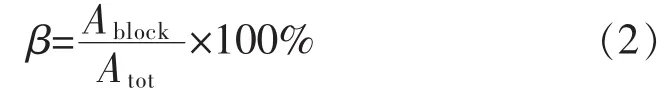
式中：Atot为隧道全断面；Ablock为隧道中的车辆阻塞断面。

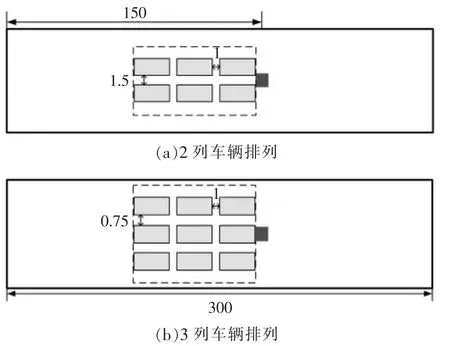
图8 隧道中车辆的布置示意图（单位：m）Fig.8 Schematic diagram of vehicle layout in tunnel （unit：m）

由表3可知，相同阻塞比下，临界风速随火源功率的增加而不断增大；对于同一火源功率隧道阻塞比越大所需临界风速就越小。

4.5 坡度对临界风速的影响

JTG D70—2004《公路隧道设计规范》关于隧道坡度的规定是：隧道坡度应大于0.3%，一般情况下应小于3%；受地形条件限制时，可适当加大，但不宜大于4%。因此，分别选取了-4%，-3%，-2%，-1%，0%，1%，2%，3%和4%共9种情况进行数值模拟。隧道坡度变化如图9所示。

根据这9种坡度，研究隧道坡度对临界风速的影响，其中正坡度为上坡，负坡度为下坡，具体的工况设置和模拟结果见表4。

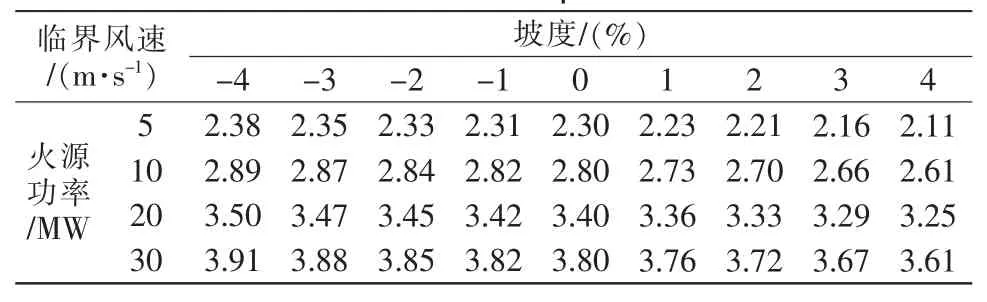
表4 不同坡度的模拟工况及测试结果Tab.4 Simulation conditions and test results of different slopes

由表4可知，相同坡度、不同火源功率时，临界风速随火源功率的增大而增大；相同火源功率、不同坡度时，下坡隧道中临界风速随坡度的增大而增大，上坡隧道中临界风速随坡度的增大而减小。

通过以上5组试验及结果分析可知，运用数值模拟试验得到的临界风速数据具有准确性和可靠性，可为公路隧道纵向通风临界风速提供理论参考值。同时，也验证了火源功率、火源宽度、火源位置、阻塞比和坡度等5个因素对临界风速影响的重要性，可以作为建立神经网络预测模型提供样本数据来源。

5 神经网络模型预测试验及其分析

在以上FDS模拟试验的基础上，建立公路隧道火灾临界风速的神经网络模型。基于对公路隧道火灾临界风速的影响因素的数值模拟计算，共获取了139组训练样本数据，为减小网络的训练时间和预测误差，将训练样本进行归一化处理。在完成神经网络训练后，将确定好最优参数的BP神经网络用于临界风速的预测。

为验证BP神经网络预测临界风速的性能好坏，选取29组（包括5个影响因素）测试样本，对网络性能加以评估，对比临界风速的预测值与FDS模拟计算值。神经网络模型预测值与FDS模拟值的对比如图10所示。

由图可见，采用神经网络模型的预测值与FDS模拟计算值具有相同的变化趋势，除个别值的差别稍大一些外，2条曲线基本相吻合，说明文中所构建的神经网络模型具有较好的预测效果。

为验证改进BP算法的性能，在相同的试验条件下运用相同的训练样本，对改进前后的神经网络模型预测性能进行比较。

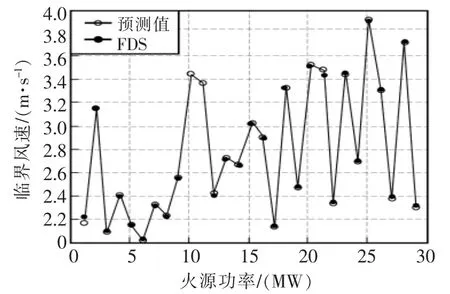
图10 神经网络模型预测值与FDS模拟值的对比Fig.10 Comparison of neural network predicted values and FDS simulated values

运用改进BP算法和标准BP算法下的预测误差对比曲线如图11所示。由图可见，改进BP算法的预测误差（除个别值）基本维持在-0.02～0.02，误差曲线变换较为平缓，平均误差为0.0112；而标准BP算法的预测误差分布在-0.21～0.11，误差范围较大。

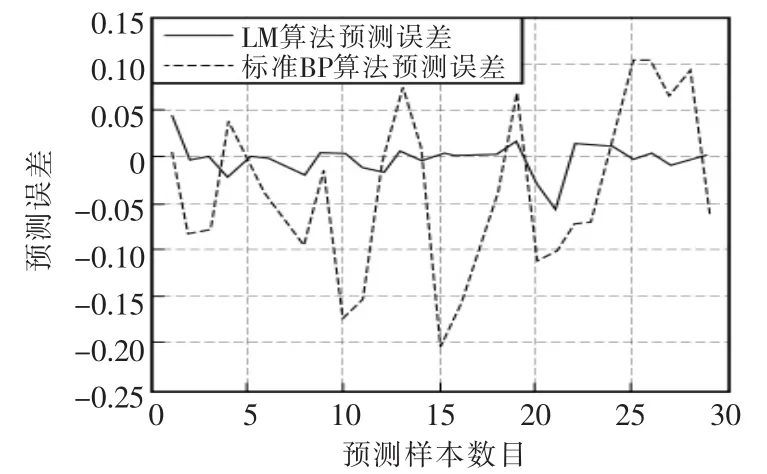
图11 误差曲线的对比Fig.11 Error curves comparison

本文预测模型与FDS模拟计算值的相对误差曲线如图12所示。由图可见，本文模型的相对误差分布在-0.02～0.025，两者之间差值非常小，在所有预测样本中，最大相对误差为0.0211。从预测误差和相对误差来看，本文模型能够很好地满足消防工程的精度需要，且相比传统数值模拟方法大大节省了时间成本。因此本文所建立的神经网络模型能够较好地预测公路隧道发生火灾时所需的临界风速。

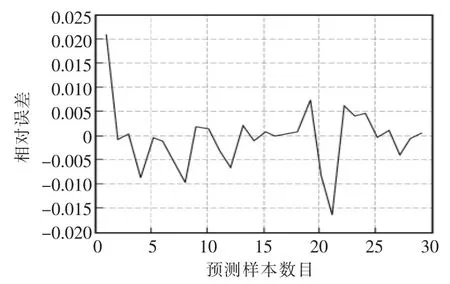
图12 相对误差曲线Fig.12 Relative error curve

6 结语

运用数值模拟的方法，系统地研究了公路隧道火灾临界风速的各种影响因素，并在此基础上应用BP神经网络技术，建立了临界风速预测模型，从而弥补了传统试验方法以及数值模拟方法的不足。性能测试结果表明，本文所建立的神经网络预测模型对临界风速具有较好的预测效果，为快速预测隧道火灾临界风速的工程计算模型提供了一种新方法。