基于模糊算法的变步长电导增量法仿真研究

李 皓，陈超波，高 嵩，李 进，李继超

（西安工业大学 电子信息工程学院，西安 710016）

提高光伏电池的利用率一直以来都是光伏发电领域的研究热点。光伏电池的利用率受外部环境条件变化的影响较大，其中光照强度、温度是较为主要的外界因素。在一定的环境条件下，光伏电池存在不同且唯一的最大功率点（MPP）[1]。对于光伏发电系统而言，应最大限度地利用光能，使光伏电池输出功率达到最大，寻求最大功率点的过程叫做最大功率点追踪（MPPT）。

最大功率点跟踪算法的种类有很多，其中电导增量法是一种经典的最大功率点跟踪算法。传统的电导增量法通常采用固定的步长，即使系统电压扰动的变化量固定。这便引出了步长设置的问题：步长越大，系统能够快速地达到最大功率点附近，但是功率震荡问题越严重；相反，步长越小，系统在稳定运行时精度越高，但会降低系统的反应速度。针对这一问题，其中一种较为简单的解决方法是根据系统运行状态改变步长大小，使系统在远离最大功率点时以较大步长运行，来提高响应速度；接近最大功率点以较小步长运行，以提高精度，这就是变步长电导增量法的基本思想。

模糊控制是一种新兴的控制方式，该方式通过专家经验来建立描述系统变量间关系的模糊法则，并通过法则规则调控系统的输出。模糊控制器的设计不需要被控对象精确的数学模型，因而较适用于动态特性不易掌握和较为复杂的系统[2]。

本文将模糊控制器应用到变步长电导增量法中，利用模糊算法实现对步长的调整，提高了系统响应速度和稳态精度。在基于Boost升压电路的模型下，利用Simulink进行仿真研究。仿真结果表明，该方法能有效地改善光伏系统的动态响应和功率震荡问题。

1 Boost电路工作原理

Boost电路是一种将输入电压升高的非隔离直直变换器[3]。Boost电路如图1所示，其电感L和电容C通常很大，假设开关周期为T，占空比为D，控制开关开通时间为DT，关断时间为（1-D）T。

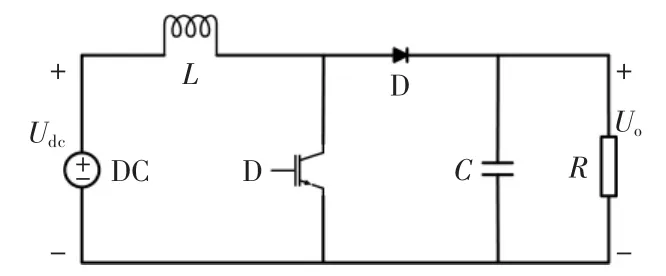
图1 Boost电路原理图Fig.1 Schematic diagram of boost circuit

当控制管导通时，电源Udc向电感L充电，此时电感电流的增量为

当控制管关断时，电感电流经续流二极管D流向输出侧，电源和电感共同向电容充电并向负载提供能量，此时，电感电流线性减小：

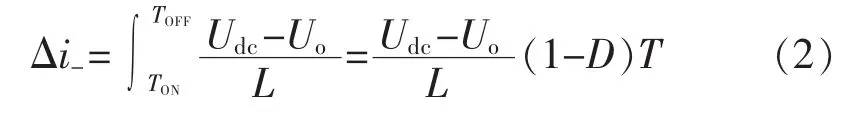
当电路稳定运行时，每个周期中电感电流的增量与减小量相等。由以上两式便可得稳态时输出电压与输入电压的关系：

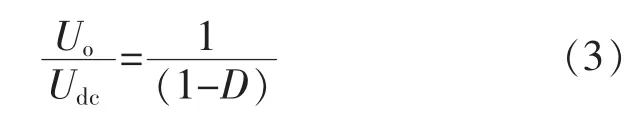
由上式可知通过改变占空比可以调控光伏电池两端电压，调节光伏电池内阻与负载电阻的匹配程度，寻找最大功率点。

2 电导增量法

光伏电池输出功率随输出电压变化而变化，最大功率点位于功率曲线的极值点处。电导增量法利用功率变化率在极值点处的特性，得到系统工作点位于最大功率点时的电导和电导变化率之间的关系。对于光伏电池，在最大功率点处有dP/dU=0，并且考虑到光伏电池的瞬时输出功率为P=UI。将上式对U求导有：

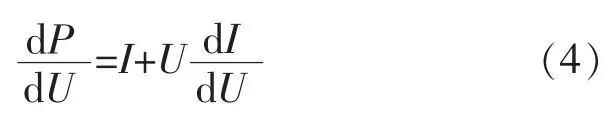
当满足最大功率点时有：

并根据当工作点位于最大功率点左侧和右侧时分别有 dP/dU＞0，dP/dU＜0，可得：

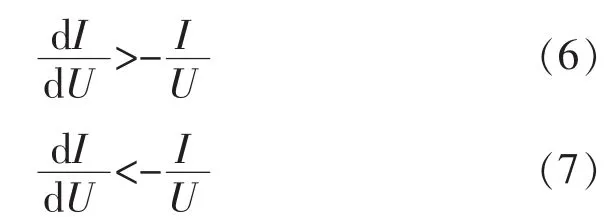
实际应用中考虑到数字控制方式，故以差分代替微分，于是有电导增量法进行最大功率点跟踪时的判据：

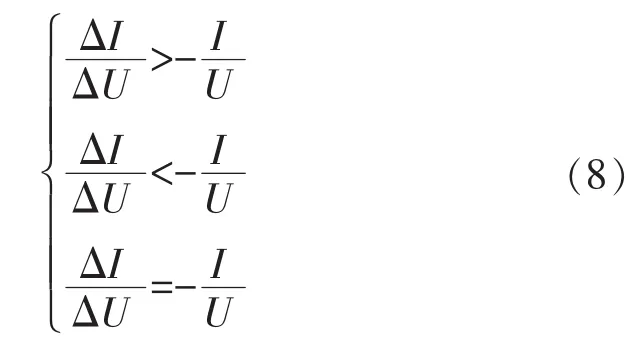
电导增量法实现流程如图2所示，其中UK、IK为第K次光伏电池输出电压和电流的采样值，ΔU为每次的电压改变量。

电导增量法通过判断ΔI/ΔU=-I/U是否成立来判断系统是否已经运行于最大功率点。对于传统的定步长的电导增量法而言，不能同时兼顾系统响应速度和在最大功率点工作时的稳定性。造成这一现象的原因是使用差分代替了微分，搜寻过程中使用一定的步长。为解决这一问题，有学者提出了改变步长的思想[4-7]。

由光伏电池的PV特性，当工作远离最大功率点时dP/d U 较大，当工作点靠近最大功率点时 dP/dU较小，变步长电导增量法通过此来改变步长[3]。一种较为简单的方法是令步长通过式（9）改变：

图2 电导增量法流程Fig.2 Flow chart of conductance increment method

其中A是比例系数，A的选取对于系统而言具有关键作用，过大过小都会影响系统的性能。其大小的选择往往通过经验和实验来决定。

3 基于模糊算法的变步长电导增量算法

3.1 基本原理

变步长电导增量算法中步长的控制由模糊控制器来实现，在传统的变步长控制方式中步长的改变为ΔU=A·dP/dU，即利用功率的变化率实现步长调节。在模糊变步长电导量算法中借鉴电导增量法的思想，用功率的全微分近似替代dP，使用E=ΔI/ΔU -I/U 来对占空比实现调控。这一方式可以视为利用电导变化率与最大功率点电导之间的大小关系调节占空比，如图3所示。

图3 P-U、U-I特性曲线Fig.3 P-U and U-I characteristic curves

I/U表示的是工作点与原点连线的斜率；而ΔI/ΔU表示弦U1与U2的斜率的绝对值。两者之间的差值反映了功率变化的大小。

模糊控制器根据输入的差值大小对步长大小进行调节。当远离最大功率点时E值较大，通过模糊控制器输出较大的步长，快速跟随系统最大功率点；当工作点接近最大功率点时E值较小，此时模糊控制器输出较小的步长，提高稳态时的精度。

3.2 确定模糊子集和隶属度函数

模糊控制器的输入为E，输出为占空比D。可将E和D分为6个模糊子集分别为E=｛NB，NS，ZE，PS，PB｝，D=｛NB，NS，ZE，PS，PB｝。 E 的模糊论域取为（-10，10），D 的模糊论域取为（-0.1，0.1），比例因子和量化因子取为68和0.1。隶属度函数均采用三角形隶属度函数，如图4、图5所示。控制器采用Mamdani推理，解模糊算法采用Centroid。

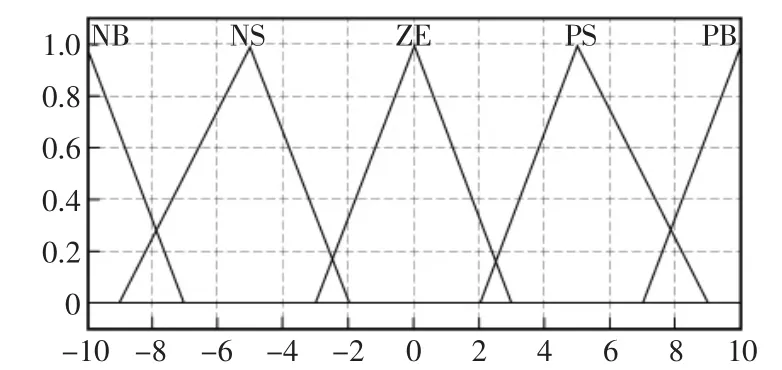
图4 E隶属度函数Fig.4 Membership function of E

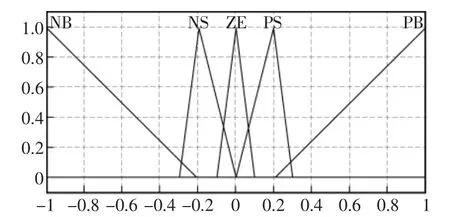
图5 D隶属度函数Fig.5 Membership function of D

3.3 模糊规则的建立

根据上述原理，模糊控制器应当遵循如下规则：

（1）当E为负值且较大时（NB），说明在最大功率点左边且较远，步长应当为正且较大（PB）；

（2）当E为负值且中等时（NM），说明在最大功率点左边且较接近，步长应当为正且中等（PM）；

（3）当 E 较小接近于零时（ZE），步长应当较小接近于零（ZE），以使系统工作在稳定状态；

（4）当 E为正值且较大时（PB），说明在最大功率点右边且较远，步长应当为负且较大（NB）；

（5）当E为正值且中等时（PM），说明在最大功率点右边且较接近，步长应当为负且中等（NM）。

依据上述规则建立规则控制表1，模糊规则曲线如图6所示。

表1 模糊控制规则表Tab.1 Fuzzy control rule table

图6 模糊规则曲线Fig.6 Fuzzy rule curve

4 仿真模型及验证

仿真模型搭建在Matlab2017a环境下，如图7、图8所示。

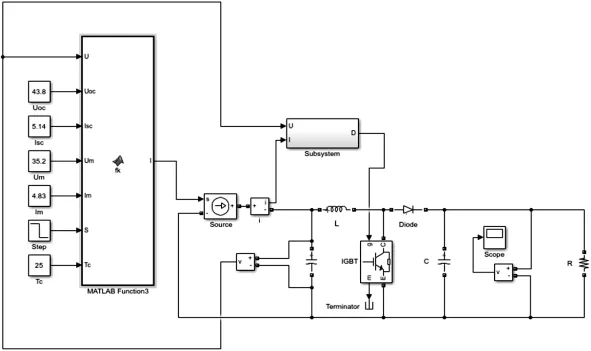
图7 仿真模型Fig.7 Simulation model

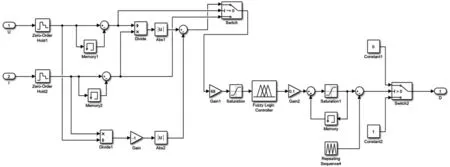
图8 MPPT模块Fig.8 MPPT module

仿真模拟了在不同的外部环境下，对比其追踪效果。仿真模型中利用Matlab编程输入Matlab function函数模块中构建太阳能电池模型[8]。所采用的太阳能光伏电池模型其开路电压为43.8 V，短路电流为5.14 A。光照条件在开始时为1000 W/m2，在t=1 s时光照从1000 W/m2突变为500 W/m2。环境温度为25℃。此外，为了对比定步长电导增量法与改进算法的差异，本文还对不同步长电导增量法进行仿真，大步长时占空比变化量设置为0.01，小步长时占空比变化量设置为0.001，对比仿真效果如图9～图11所示。

从以上仿真图中可知：

（1）大步长电导增量法在0.2 s左右进入稳定状态，当进入稳定运行状态时，功率波动明显。在光照条件改变后，系统在经过0.2 s左右再次达到稳定运行状态。大步长电导增量法能使系统有效的追踪最大功率点，但稳定状态下功率波动较大。

（2）小步长电导增量法在0.5 s左右进入稳定状态，当进入稳定运行状态时，功率波动不明显。在光照条件改变后，系统在经过0.2 s左右再次达到稳定运行状态。小步长电导增量法能使系统有效的追踪最大功率点，但追踪速度较慢。

（3）模糊变步长电导增量法在0.2 s左右进入稳定状态，在稳定状态运行时，功率波动不明显。在光照条件改变后，系统经过0.1 s左右再次进入稳定状态。速度快，稳定性高。

图9 小步长电导增量法波形Fig.9 Small step conductance incremental waveform

图10 大步长电导增量法波形Fig.10 Large step conductance incremental waveform

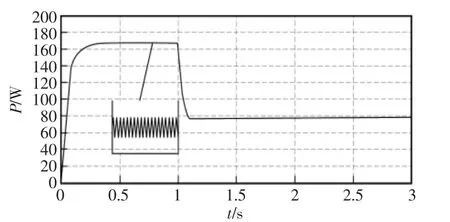
图11 模糊变步长电导增量法波形Fig.11 Fuzzy variable step conductance increment method waveform

对比模糊变步长法与定步长法的仿真结果可以得出以下结论：模糊变步长法在光照条件发生改变时能有效的改变系统运行步长使系统同时兼具较快的速度和良好的稳定性。

5 结语

本文在Matlab/simulink环境下采用模糊变步长电导增量法搭建了最大功率点追踪模型。在继承了传统定步长电导增量法的基础上，利用调节步长的思想，通过模糊控制器根据利用电导变化率与最大功率点电导之间的大小关系调节步长大小。使光伏发电系统能根据环境状态的变化及时调节步长，有效平衡了系统反应快速性与稳定性之间的矛盾。在对比模糊变步长及两种不同步长电导增量法的前提下，仿真结果表明模糊变步长方法对改善追踪效果的有效性。