饲料原料粉体流动特性预测模型

陈计远，王红英，金 楠，方 鹏，段恩泽，常楚晨

（中国农业大学工学院，国家农产品加工技术装备研发分中心，北京 100083）

0 引 言

饲料加工过程中大量涉及到对粉体物料的处理过程。从原料粉碎后进入中间配料仓，到连接各工艺流程的供料设备，再到混合机，饲料原料均是粉体状态，并具有相应的粉体流动特性[1-4]。此类原料在运输与储存过程中，由于颗粒间的作用力，常会出现结拱、鼠洞、流率低甚至是堵塞的问题。例如，中间配料仓尺寸及出料口尺寸设计不合理导致结拱、鼠洞问题[5-6]；供料设备管道设计不合理导致无法连续、稳定供料，影响生产；对混合机内粉体颗粒间作用力不清，导致无法保证混合均匀度且会增加筒内物料残留量[7]。另外，利用离散元方法对输送设备或混合机进行模拟仿真时，缺乏粉体颗粒间内聚力及摩擦角的准确数值会导致模拟结果与实际值的较大偏差。上述问题的解决均需要对不同粉料的流动特性进行探究。

粉体的流动特性是粉体工程的基础，在涉及到粉体工程的设计及操作中，对粉体流动特性的研究十分广泛[8-9]。Xu 等[10]使用休止角、豪斯纳率和压缩指数表征4 种生物质粉料的流动特性，探究了粒径、颗粒形状、物料种类对粉体流动特性的影响。Saker 等[11]使用粉体剪切测试仪测定了9 种常用食品添加剂粉料的流动特性，并提出豪斯纳率可以较好的表征上述物料的流动特性。郑忆南等[12]通过测试煤粉的内聚力、稳态内摩擦角对不同气化工艺煤粉的流动特性进行了研究，并探究了粒径和细颗粒含量对煤粉流动特性的影响。有研究测定了4 种药物原料及混合粉料的卡尔指数和豪斯纳率，对比了原料粉料与混合后粉料的流动特性差异。

在饲料加工领域，现有研究大多集中在粒状原料储存筒仓内物料的流动特性研究，对于经粉碎机粉碎后的粉状原料，其输送及加工过程中的流动特性研究鲜有报道。刘克瑾等[5]利用离散元法探究了大豆在筒仓内受力分布及卸料过程中大豆颗粒的流动情况。袁洪岭等[13]和黄辉[14]均总结了饲料厂中筒仓结拱原因及防治措施，但未深入探究筒仓内物料特性与结拱形成原因的关系。

综上，本文采用粉体流动测试仪研究了2 种主要饲料原料(豆粕和玉米DDGS)在不同筛孔直径、含水率和固结应力条件下的流动特性变化规律，分析了粉碎粒度、含水率和固结应力3 因素对饲料原料流动特性的影响，并建立了3 个因素关于内聚力的预测模型，以期为中间配料仓、供料设备的设计和混合机加工参数的选择提供基础数据和理论依据。

1 材料与方法

1.1 试验材料

选取畜禽饲料配方中占比较大的2 种原料：豆粕和玉米DDGS，并分别使用配备1.5、2.0 和2.5 mm 筛孔直径的粉碎机进行粉碎，获得相应粒度的粉状原料。

原料经粉碎后含水率为10%左右，经混合机混合后含水率为14%左右[1-2]，因此本研究中粉料含水率（湿基）梯度设置为10%、12%和14%。分别通过自然晾干和赋水处理获得相应含水率的粉体物料[3]。筒仓中的饲料原料所受应力随高度的增加而增大，本试验结合实际生产中粉料所受的应力水平大小将固结应力范围设置为1~3 kPa。

1.2 试验仪器

15B 型万能粉碎机：江阴市宏达粉体设备有限公司；电热恒温干燥箱：上海精宏实验设备有限公司；电子精密天平：梅特勒-托利多仪器有限公司；Mastersize3000激光粒度仪：英国Malvern 公司；PFT 粉体流动测试仪：美国Brookfield 公司。

1.3 试验方法

本试验使用激光粒度仪测量饲料原料的粒径分布，由于试验物料吸水膨胀会导致测量误差，故采用干法测量。为避免含水率过高影响粉体颗粒的分散效果，需将试样于40 ℃烘干12 h 至仪器要求的含水率（湿基含水率<8%）后再进行测量。

本试验中使用PFT 粉体流动测试仪的流动函数测试单元测定饲料原料的流动特性，具体操作参照其标准测试方法进行[15]。流动函数测试被广泛应用于粉体流动特性的表征，反映了粉体在某一压缩状态下发生初始流动的难易程度，莫尔圆常被用来分析相关数据。基于正应力σ 与切应力τ 的数据，利用Mohr-Coulomb 方程进行线性回归，得到相应预应力下的屈服轨迹：

上述方程可以得到内聚力FC和有效内摩擦角φe，绘制最小摩尔半圆经过坐标原点，并与屈服轨迹相切，获得无侧限屈服强度σc值；过极限应力状态点绘制最大摩尔半圆，得到最大主应力值σ1。不同的预压缩应力将得到不同的屈服轨迹，每一条屈服轨迹都可以得到一组无侧限屈服强度σc和最大主应力σ1。通过多组无侧限屈服强度σc和最大主应力σ1得到粉体流动函数[16-17]。流动函数的倒数定义为流动指数ffc，即

基于流动性指数，可以将粉体划分为非流动(harded)、强黏附性(very cohesive)、黏附性(cohesive)、易流动(easy flowing)和自由流动粉体(free flowing)。

1.4 数据处理

采用SPSS19.0 对试验结果进行主效应分析和回归模型的构建，采用Origin2017 作图。

2 结果与分析

2.1 饲料原料粒度分布特征

豆粕和DDGS 的粒度分布特征测试结果如表1 所示，豆粕的比表面积平均粒径D[3,2]的范围为198~349 μm，体积平均粒径D[4,3]的范围为577~986 μm，DDGS 的D[3,2]范围为297~340 μm，D[4,3]的范围为532~641 μm；D10、D50、D90 分别表示样品的累计程度分布达到10%、50%、90%时所对应的粒径[18]，豆粕的D10、D50、D90范围分别为113~278，541~844，1 050~1 910 μm，DDGS的D10、D50、D90 范围分别为173~193，477~541，1 090~ 1 210 μm。Span=(D90-D10)/D50，反映了颗粒粒度分布的宽度即不同粒径颗粒的分散程度，此数值越大说明颗粒粒径越不集中于平均粒径，粉碎均匀度较差,豆粕与DDGS 粒径分布均属于较宽的范畴；DDGS 粒度分布规律与豆粕相似，且均呈单峰分布，这与生物质粉料大多呈双峰分布的规律不同[10]，但与多数食品添加剂的单峰分布规律类似[19]。

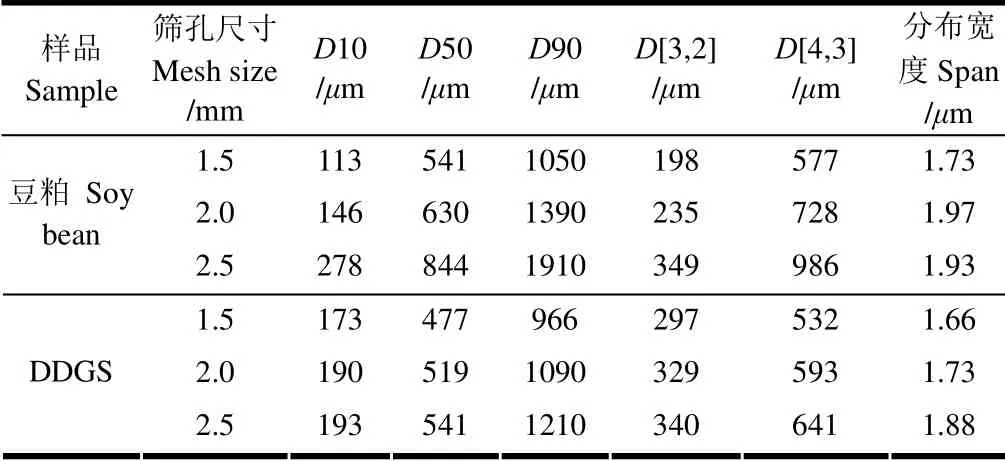
表1 豆粕和DDGS 粉体粒径分布 Table 1 Particle size distribution of soybean powder and DDGS powder

2.2 固结应力对饲料原料流动性的影响

图1a、1b、1c 分别为3 种粉碎粒度的豆粕在10%、12%和14%含水率下内聚力随固结应力变化的曲线，图1d、1e、1f 分别为3 种筛孔直径的DDGS 在10%、12%和14%含水率下内聚力随固结应力变化的曲线。随着固结应力增大，3 种筛孔直径豆粕粉料的内聚力分别在0.127~0.366、0.119~0.350、0.113~0.340 kPa 范围内变化；DDGS 粉料的内聚力变化范围为 0.135~0.500、0.132~0.430、0.125~0.407 kPa。以图1a 中含水率14%的豆粕为例，随着固结应力由1 增加到3 kPa,内聚力由0.150增加至0.366 kPa，即豆粕粉料的流动性逐渐变差；在 1 kPa 固结应力水平下，3 个含水率水平下的内聚力差异较小，而在3 kPa 固结应力水平下，3 个含水率水平下的内聚力差异较大。其余筛孔直径及含水率水平下的豆粕表现出同样的规律，DDGS 表现出同样的规律。这是因为颗粒间的内聚力来源包括静电作用力、范德华力和液桥导致的毛细管力。当作用于粉体的固结应力增大时，颗粒间的间距由于压缩而减小，导致范德华力增加而阻碍两颗粒间的相对运动，从而使得粉体整体上表现为流动性变差；另外，固结应力增大造成颗粒体的压缩形变，将引起颗粒间的接触面积增大，同样会导致颗粒间范德华力的增加，从而使得粉体流动性变差[20]。

上述结论与许多文献资料关于粉体物料流动性的研究报道一致。Saker 等[19]的研究表明随着固结应力的增加，2 种乳糖颗粒和2 种微晶纤维素颗粒的豪斯纳率及内聚力呈非线性增加趋势，即流动性逐渐变差。Xu 等[10]的研究显示随着固结应力的增加，秸秆粉料的密度增加，进而导致粉体流动性变差。

图1 豆粕与DDGS 粉料的内聚力随固结应力变化的曲线 Fig.1 Variation in cohesion with consolidation stress of soybean and DDGS

2.3 筛孔直径对饲料原料流动性的影响

图2 a、2b、2c 分别为3 种固结应力的豆粕在10%、12%和14%含水率下内聚力随筛孔直径变化的曲线，图2d、2e、2f 分别为3 种固结应力水平下的DDGS 在10%、12%和14%含水率下内聚力随筛孔直径变化的曲线。粉碎样品的最终粒度由筛孔直径决定，所以本节主要讨论粉碎粒度与内聚力的关系。3 种固结应力豆粕粉料的内聚力分别在0.113~0.150、0.129~0.216、0.245~0.366 kPa 范围内变化；DDGS 粉料的内聚力变化范围为0.125~0.158、0.170~0.300、0.301~0.500 kPa。以图2a 中含水率14%的豆粕为例，随着筛孔直径的增加，内聚力由0.150 减小至0.140 kPa，即随着粉体颗粒粒径的增加，粉体流动性逐渐增加。可能的原因是随着粒径减小，粉体堆积更加紧密，堆积密度相应增大，孔隙率降低，，因而颗粒间的配位数增大，导致颗粒间的内聚力增加，从而表现出流动性变差的规律[20]。利用粉体床层团聚强度的概念同样可以解释上述现象，粉体的团聚强度与颗粒的粒径成反比关系，故粉体的流动性随着筛孔直径的减小而变差。

上述结论与许多文献中的报道一致。Xu 等[10]研究表明，玉米秸秆、大豆秸秆和稻壳粉料的流动性随粒度的增加呈现非线性增加的规律。Wang 等[21]研究表明煤粉的流动性随着粉体粒度的减小而变差。Lu 等[22]的研究同样表明平均粒径范围为47 ~234 μm 煤粉的流动性随平均粒径的减小而变差。Guo 等[23]的研究显示研磨得到的水稻秸秆的粉体流动性随平均粒度的减小而变差。Xu 等[24]的研究显示玻璃晶体同样具有类似上述的性质。

图2 豆粕与DDGS 粉料的内聚力随筛孔直径变化的曲线 Fig.2 Variation in cohesion with mesh size of soybean and DDGS

2.4 含水率对饲料原料流动性的影响

3 个含水率水平(10%、12%和14%)的豆粕粉料和DDGS 粉料的实测含水率如表2 所示。

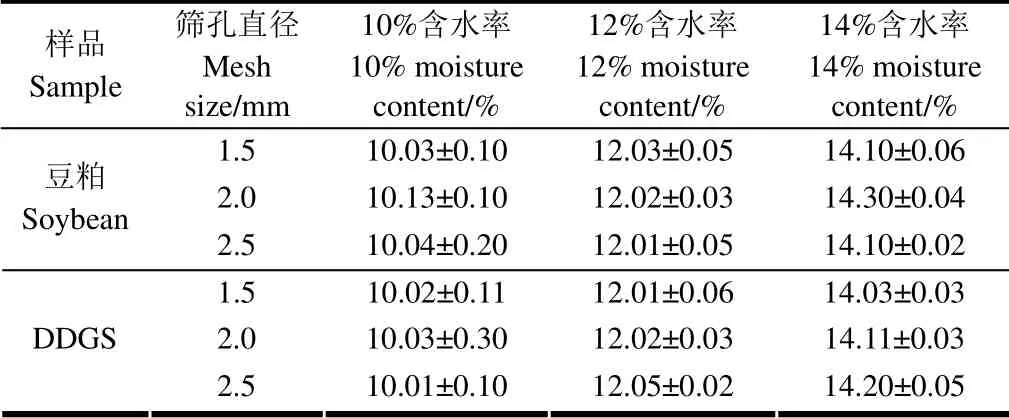
表2 试样的实测含水率(湿基) Table 2 Practical moisture content of sample(wet basis)

图3a、3b、3c 分别为3 种固结应力的豆粕在1.5、2.0和2.5 mm筛孔直径下内聚力随含水率变化的曲线，图3d、3e、3f 分别为3 种固结应力水平下的DDGS 在1.5、2.0和2.5 mm 筛孔直径下内聚力随含水率变化的曲线。随着含水率增大，3 种固结应力豆粕粉料的内聚力分别在0.113~0.150、0.129~0.216、0.245~0.366 kPa 范围内变化；DDGS 粉料的内聚力变化范围为 0.125~0.158、0.170~0.300、0.300~0.500 kPa。以图3a 中筛孔直径2.5 mm豆粕为例，含水率从10%增加至14%，内聚力从0.129增加至0.15kPa，从而表现出流动性变差的规律。这是因为随着含水率的增加，颗粒间的毛细管力增加，进而显著增加颗粒间的粘附力，从而降低粉体的流动性。

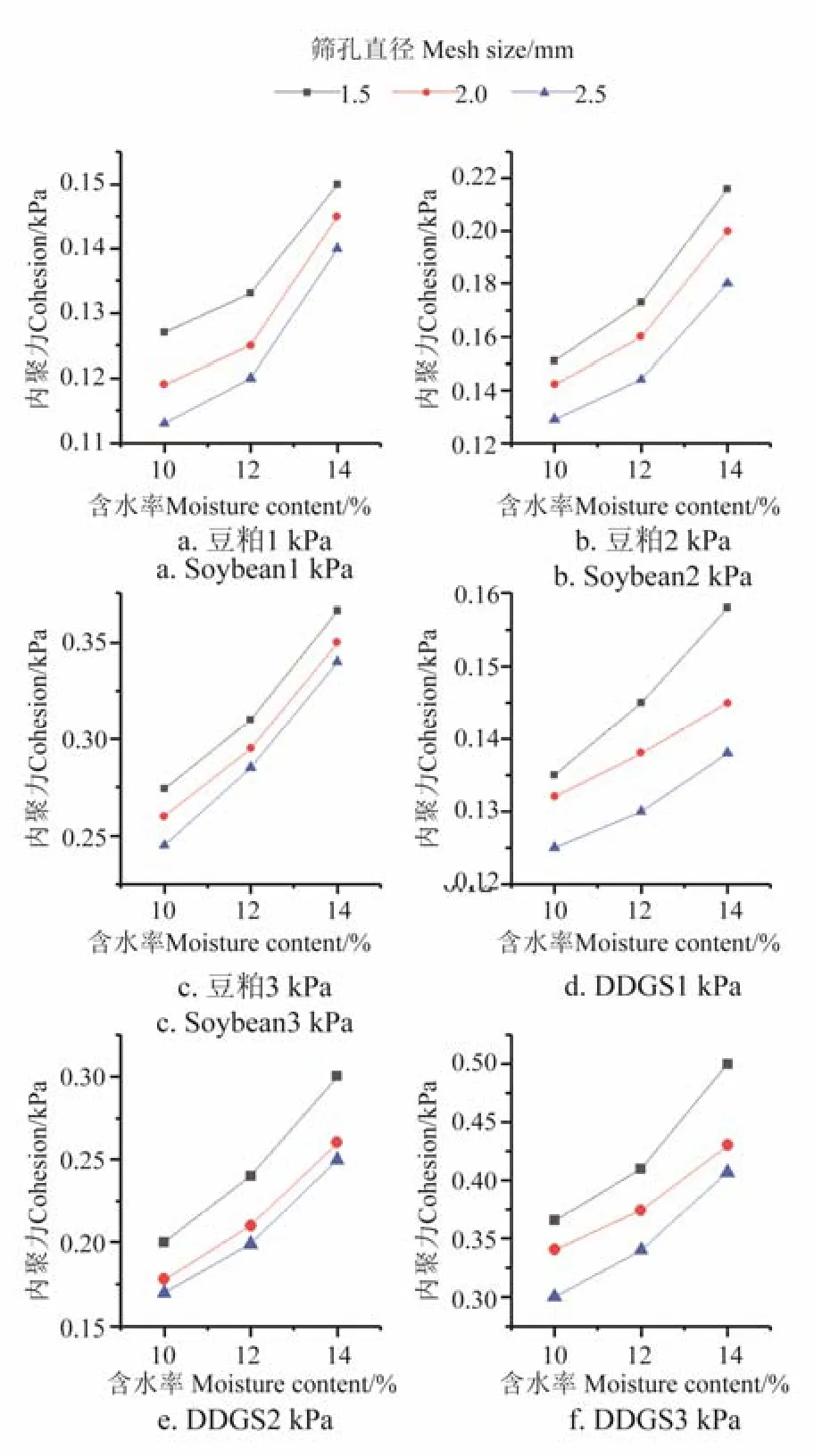
图3 豆粕与DDGS 粉料的内聚力随含水率变化的曲线 Fig.3 Variation in cohesion with moisture content of soybean and DDGS

Crouter 等[25]研究表明，微晶纤维素、甲基纤维素和羟甲基纤维素等6 种药物赋形剂的流动性随含水率的增加而非线性减小。Etti 等[26]研究显示4 种药用草本植物的粉体流动性随着含水率的增加而变差。Fitzpatrick 等[27]的研究表明茶叶粉料具有类似的性质。

2.5 流动函数及流动特性预测模型的建立

根据流动指数ffc的大小可对粉体流动性进行分类[28]，非流动(0≤ffc<1)、强黏附性(1≤ffc<2)、黏附性(2≤ffc<4)、易流动(4≤ffc<10)和自由流动粉体(ffc≥10)。如图4a 所示为3 种粒径和3 种含水率共9 类豆粕粉料的流动函数（P1为1.5 mm 筛孔直径，10%含水率，P2 为2.0 mm 筛孔直径，10%含水率，P3 为2.5 mm 筛孔直径，10%含水率，P4 为1.5 mm 筛孔直径，12%含水率，P5 为2.0 mm 筛孔直径，12%含水率，P6 为2.5 mm 筛孔直径，12%含水率，P7 为1.5 mm 筛孔直径，14%含水率，P8 为2.0 mm 筛孔直径，14%含水率，P9 为2.5 mm 筛孔直径，14%含水率）。所有试样均落在黏附性和易流动区域，如图4b 所示为3 种筛孔直径和3 种含水率共9 类DDGS 粉料的流动函数，所有试样均落在黏附性和易流动区域[29]，这与多数食品物料所落区域相同[29-30]，这也说明了利用内聚力表征粉体流动特性的可行性[22,31]。但未表现出类似2.3及2.4 节明显的规律性，故可将流动函数表征方法作为定性分析的手段。

图4 豆粕和DDGS 粉料的流动函数曲线 Fig.4 Flowability function curve of soybean and DDGS

由因素主效应分析（表3 和表4）可知，豆粕及DDGS的流动性显著受固结应力、含水率、筛孔直径(P<0.01)以及三者的交互作用的影响(P<0.01)。

以本试验中的所有内聚力数据为基础，利用SPSS 软件对2 种饲料原料的内聚力进行多元回归拟合，得到以下方程：

豆粕：

回归方程的R2均在0.957 以上，可见模型对于预测豆粕和DDGS 粉体的内聚力具有良好效果，可以用以预测此2 种饲料原料的流动特性。

表3 豆粕粉料内聚力的主效应分析 Table 3 Analysis of variance on cohesion of soybean powder

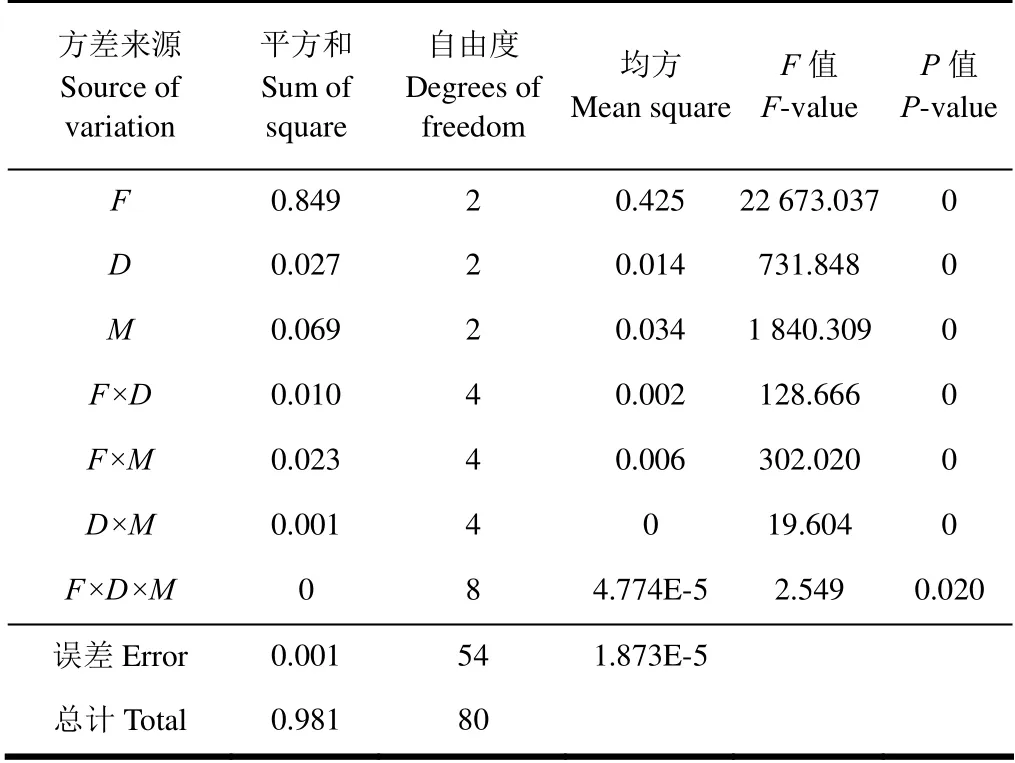
表4 DDGS 粉料内聚力的主效应分析 Table 4 Analysis of variance on cohesion of DDGS powder

3 结 论

1）豆粕粉料和DDGS 粉料的流动性均显著受固结应力(1~3 kPa)、含水率(10%~14%)、筛孔直径(1.5~2.5 mm)以及三者交互作用的影响。各因素的主次顺序为固结应力>含水率>筛孔直径。

2）豆粕粉料的内聚力随着含水率及固结应力的增大而增大，随着筛孔直径的增大而减小，即豆粕粉体的流动性随含水率及固结应力的增加而变差，随筛孔直径的减小而变差。DDGS 粉料表现出类似的规律。

3）基于试验数据建立了内聚力关于含水率、固结应力、筛孔直径的多元回归模型(R2>0.957)，对饲料原料粉体在此研究变化范围内的流动性具有较好的拟合效果。