GNSS 双天线结合AHRS 测量农田地形

景云鹏，刘 刚，金志坤

（1. 中国农业大学现代精细农业系统集成研究教育部重点实验室，北京10083； 2. 中国农业大学农业农村部农业信息获取技术重点实验室，北京 100083）

0 引 言

基于GNSS 的农田平整技术对节水灌溉、土地利用和保肥增产有重要的作用，是现代精细农业的重要研究内容之一[1-2]。地形测量是农田平整作业的必要环节，通过对未平整农田的地势进行测量，得到准确的位置和高程信息，可用于农田平整路径规划，同时为平整工作中挖填土方的计算和作业效果的评价提供技术支持[3-5]。

当前，适用于农田平整的地形测量设备主要包括三维激光扫描仪[6-7]、激光雷达[8]、水准仪[9]和 GNSS（global navigation satellite system，全球导航卫星系统）。GNSS 可安置在农用车辆上实时获取位置信息，多用于农机导航、农田采样和农田地图测绘。国内外学者在应用GNSS 测量农田地形方面进行了较深入的研究，Clark 等[10]使用RTK-GPS 快速获取地形数据并插值成图，在113 m²的土地上测量大约30 m 网格的高程数据，高程误差为9 cm。Yao 等[11]利用亚米级水平位置精度的GPS 对农田地形图进行测量，得到的垂直误差标准差为10～12 cm。李益农等[12]利用GPS 代替人工水准仪测量田间高程，通过对比分析得出，根据GPS 测量数据进行土地平整工程设计，其平地土方总量相对误差在8%以内。孟志军等[13-14]设计了基于RTK-GPS 的机载式农田三维地形测量系统，并验证系统在车辆低速且匀速的行驶状态下测量精度更高。李宏鹏[15]将RTK-GPS 定位技术与农田地形测量方法集成，开发了基于GNSS 的农田快速地形测量系统，获得小于1cm 的静态高程测量精度。上述研究多侧重于对GNSS 测量的地形数据直接进行插值、模型预测或聚类等分析，最终得到体现地势信息的地形图。目前基于GNSS 的农田平整系统多使用单天线进行地形测量，通常将定位天线放置平地铲的中间。这种方法忽略了农田平整过程中由于系统机械振动、平地铲的姿态改变以及地形起伏等外界因素引起的数据采集误差，降低了农田三维地形测量精度。

本文对当前的GNSS 单天线农田测量方法进行改进，采用GNSS 双天线定位定向技术获取农田地势信息，使用AHRS 测量的加速度数据校正分析GNSS 得到的农田地势信息，分析了系统结构与地形变化引起的测量误差。研制了集成地势信息获取与误差处理功能于一体的地形测量系统，并进行了农田地形测量试验。

1 地形测量原理

1.1 地势数据获取方法

分别将GNSS 定位、定向天线放至平地铲车的两端，将姿态航向传感器MTI300_AHRS 通过垫片固定在同一水平面，其空间位置分布如图1 所示。定位天线、定向天线和姿态航向传感器位于同一基线O1O2上，双天线分别位于铲车2 个支撑轮的中心线与O1O2的垂直交点上，距离为L。地形测量过程中，将测量车轮行驶路径上的地势点作为输入量，由于定向天线无法输出位置信息，根据定位天线的空间位置进行坐标转换和平移，获得另一侧车轮所对应定向天线的位置信息。

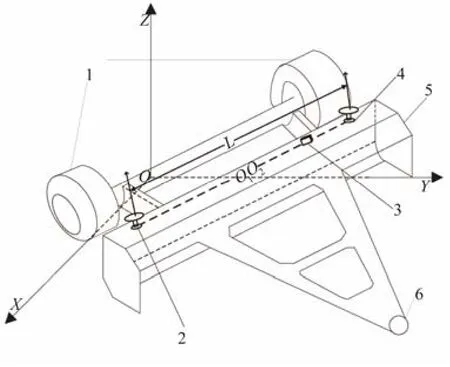
图1 地形测量平台的组成 Fig.1 Composition of topographic survey platform

地形数据的动态采集过程中，平地铲通过牵引式结构与拖拉机相连接。由于地形变化的影响，2 个卫星天线的姿态会随着平地铲一起发生变化[16-17]。在三维坐标系中通过平地铲左端定位天线的地势测量数据得到其位置信息矩阵为M'=(XM'，YM'，ZM')T，为求得定位天线在世界坐标系中的位置矩阵M=(XM，YM，ZM)T，根据AHRS实时测得的翻滚角、俯仰角、航向角信息，建立GNSS天线与AHRS 绕X、Y、Z 轴旋转的矩阵RX、RY、RZ，同时可计算出总旋转矩阵R[18-19]：

式中θR为翻滚角，(°)；θP为俯仰角，(°)；θY为航向角，(°)。

定位天线的位置坐标矩阵M=RM’，为求得另一侧支撑轮所对应的定向天线的位置坐标矩阵N=(XN，YN，ZN)T，再通过矩阵平移变换[20]计算：

式中S 为定位天线向定向天线做平移变换时的平移矩阵，XM、YM、ZM为GNSS 定位天线在三维坐标系中的坐标值，m；

GNSS 双天线也可测得自身的航向角，其角度以正南方向为0°、正西方向为90°、正北方向为180°、正东方向为270°，角度顺时针递增。将经纬度转换成平面坐标时，以正东方向为X 轴，正北方向为Y 轴构建平面坐标系。结合式（1）～（3），可得到GNSS 双天线的位置解算方程组：

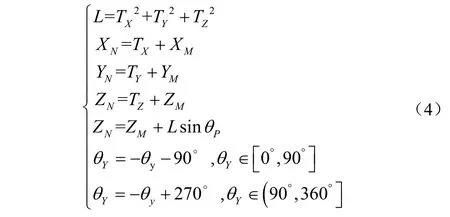
式中TX为GNSS 定位天线沿X 轴平移至定向天线的距离，m；TY为GNSS定位天线沿Y轴平移至定向天线的距离，m；TZ为GNSS定位天线沿Z轴平移至定向天线的距离，m；θy为GNSS 双天线测得的航向角，(°)。

1.2 误差分析与处理

研究发现，基于GNSS 的农田地势信息采集误差主要包括微地形误差和机械振动误差。微地形误差即由于农田局部凹凸变化而产生的测量误差，前人的研究中认为地形测量时的农田表面是连续的，即整体趋势呈高低起伏[21-22]。但实际上农田的表面并非光滑，局部地势不断变化。未平整之前存在的凹凸、小坑和小包等，微地形变化会使得采集的数据偏离真实值。机械振动误差是在拖拉机牵引平地铲行驶过程中产生的，由于拖拉机与平地铲属于销轴式半钢性连接，且缺少减震装置，平地铲会产生无规则的机械振动。该随机振动产生的位移偏差叠加至卫星天线采集到的位置信息中，进而影响测量数据精度。

本文将微地形误差与机械振动误差统称为振动误差，振动误差可以通过振动加速度进行衡量。计算分析AHRS 获取的平地铲三轴加速度信息，得出的位移变化信号即为振动误差[23-24]，本文振动误差的处理步骤如下：

1）振动加速度的测量。将AHRS 测得的平地铲三轴振动加速度Xa 、Ya 、Za 通过角度与位移变换（坐标变换矩阵详见1.1 节），可得到定位天线和定向天线的振动加速度。设AHRS 获取的振动加速度为A=(aX，aY，aZ)T，则：

式中aX、aY、aZ分别是在X、Y、Z 轴上的振动加速度；AM和AN分别是GNSS 定位天线和定向天线的振动加速度；A 是AHRS 测量的振动加速度，m/s²。

2）加速度趋势项预处理。实际测量过程中由于温度变化、农田湿度、电力磁场、GNSS 信号干扰等因素，会导致AHRS 测量的振动信号产生零点漂移和偏离基线等现象。这些现象会降低振动加速度的测量精度，为消除这些趋势项的影响，本文采用最小二乘法对振动加速度进行处理。设采集的振动加速度数据为振动拟合系数为根据最小二乘法原理可知，将m 阶多项式kc 与振动加速度信号进行拟合，以多项式与原始振动信号的误差平方和最小为目标，计算求得对应的拟合系数ib 。最后将原始振动加速度与对应多项式做差，即可得到预处理后的振动加速度，即：

式中ak为第k 个点的振动加速度，m/s²；ak’为第k 个点消除趋势项后的振动加速度，m/s²；n 为正整数；bi为第i阶的拟合系数；ck为第k 个点的拟合多项式；m 为非负整数。

3）基于频域的振动位移求解。将消除趋势项后的振动加速度进行二次积分可获得振动位移信号。前期研究表明，由于在时域中进行二次积分会产生新的误差趋势项从而影响积分效果，本文选用基于快速傅里叶变换（fast fourier transform, FFT）的频域积分方法对振动位移进行求解。计算步骤如下：

一次积分求得速度信号：

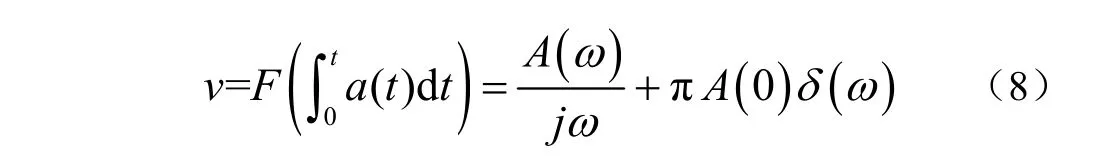
二次积分求得振动位移信号：

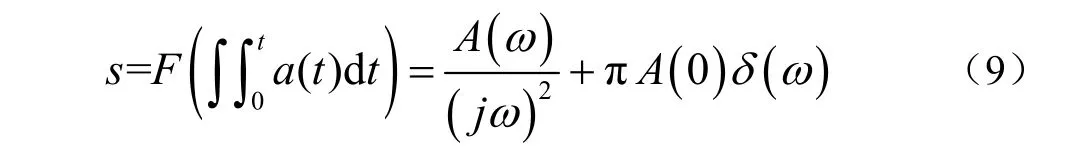
式中t 为采样时间，s；ω 为角频率，rad/s；a(t)为时域中的加速度，m/s²；A(ω)为频域中的加速度，m/s²；v 是速度，m/s；s是位移，m；，j为单位虚数；δ(ω) 为脉冲函数。

由于振动信号为离散数据，若求积分值，需先求得频域中的角频率

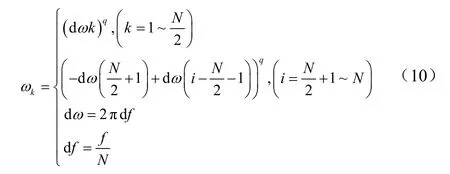
式中N 为振动信号的采集总数，f 为采集频率，Hz；q 为积分次数，则积分的频域变换为

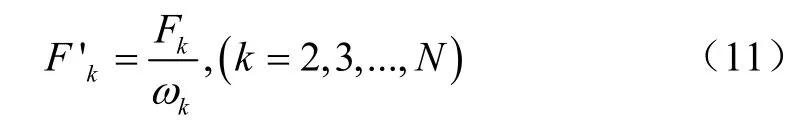
积分的相位变换为

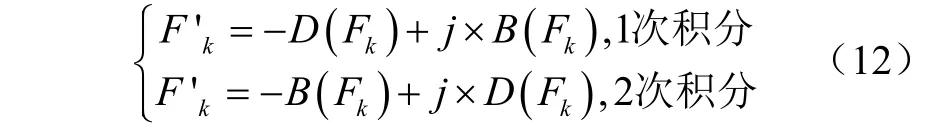
式中Fk表示第k 个点在频域的振动加速度；Fk’为Fk积分变换之后；虚数单位j 在频域中表示相移，D 为Fk的实部，B 为Fk的虚部。每次乘以一个j 就逆时针旋转90°，除以一个j 顺时针旋转90°。结合式（8）～（9）可知，在频域中一次积分顺时针旋转90°，二次积分顺时针旋转180°。将最终得到的复数数组通过傅里叶反变换至时域，即可得到所求振动位移。

4）数据平滑处理。田间试验环境会对测量仪器造成较大影响，长时间采集的高程信号会出现毛刺现象，对最后求得的高程值进行数据平滑处理有利于提高高程曲线的信噪比与光滑度[25]。由于系统数据为等间距采集，以时间为自变量，则时间间隔为定值。本文选用基于最小二乘的五点三次平滑法进行处理，设不同时刻所得到的高程值为五点三次平滑法的表达式为

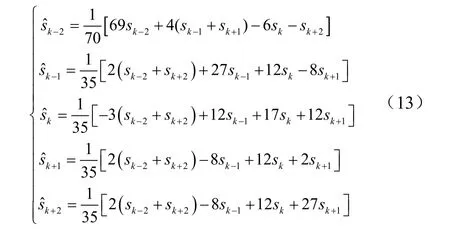
式中sk为第k 个点的高程值，m。

2 GNSS 双天线结合AHRS 测量农田地形的硬件平台与软件算法

2.1 硬件平台

本文以中国农业大学精细农业研究中心前期开发的GNSS 智能农田平整系统为试验平台，使用John Deere 公司的5-904 拖拉机作为牵引动力。采用北京盛恒天宝公司生产的平地铲（具有独立式液压结构，铲车宽度为2.5 m），上海华测导航公司生产的GNSS 双天线导航定位系统（平面测量精度为0.8 cm+1mm，高程测量精度为1.5 cm+1mm，航向精度为0.1°）；AHRS（荷兰Xens 公司生产型号为MTi-300）横滚角和俯仰角的静态测量精度为0.2°，航向角的测量误差为1°，加速度的静态测量误差为0.02 m/s²。GNSS 农田平地机及地形测量平台的组成如图2 所示。

2.2 软件算法

为保证数据运算速度，采用Visual Studio 2008 的C++语言作为系统的编译环境，利用Matlab Compiler 编译器将绘制农田三维地形图的M 函数文件转换为Visual环境可调用的形式，以提高软件系统的集成度，图3 为软件程序的流程图。

图2 GNSS 农田平地机及地形测量平台的组成 Fig.2 Composition of GNSS land leveler and topographic survey platform

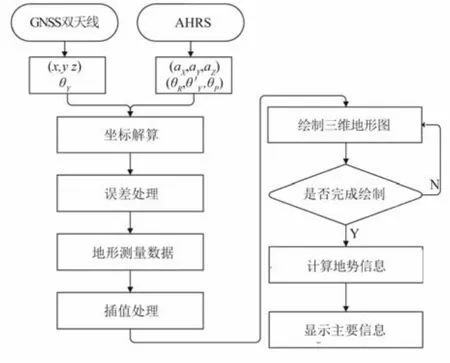
图3 农田三维地形测量程序流程图 Fig.3 Flow chart of farmland 3D topographic survey program

3 地形测量试验与结果分析

3.1 水泥路面试验与结果分析

为检验在机械振动影响下，GNSS 双天线位置解算方程和误差处理方法的效果，本文于2019 年9 月底在中国农业大学上庄试验站进行水泥路面的试验验证。分别选取长度为300、900 和1800 m 的水泥路面，拖拉机的行驶速度保持在1.12 m/s，数据采集频率为5 Hz。3 条路径中定向天线通过位置解算和误差处理前后的高程测量效果如图4 所示，表1 为定位、定向天线的高程测量结果。并以误差和来评价通过误差处理后定位天线和定向天线的高程变化情况[26-27]：

式中E 为误差和，m；Hi为第i 个测点误差处理前的高程值，m；hi为第i 个测点误差处理后的高程值，m。

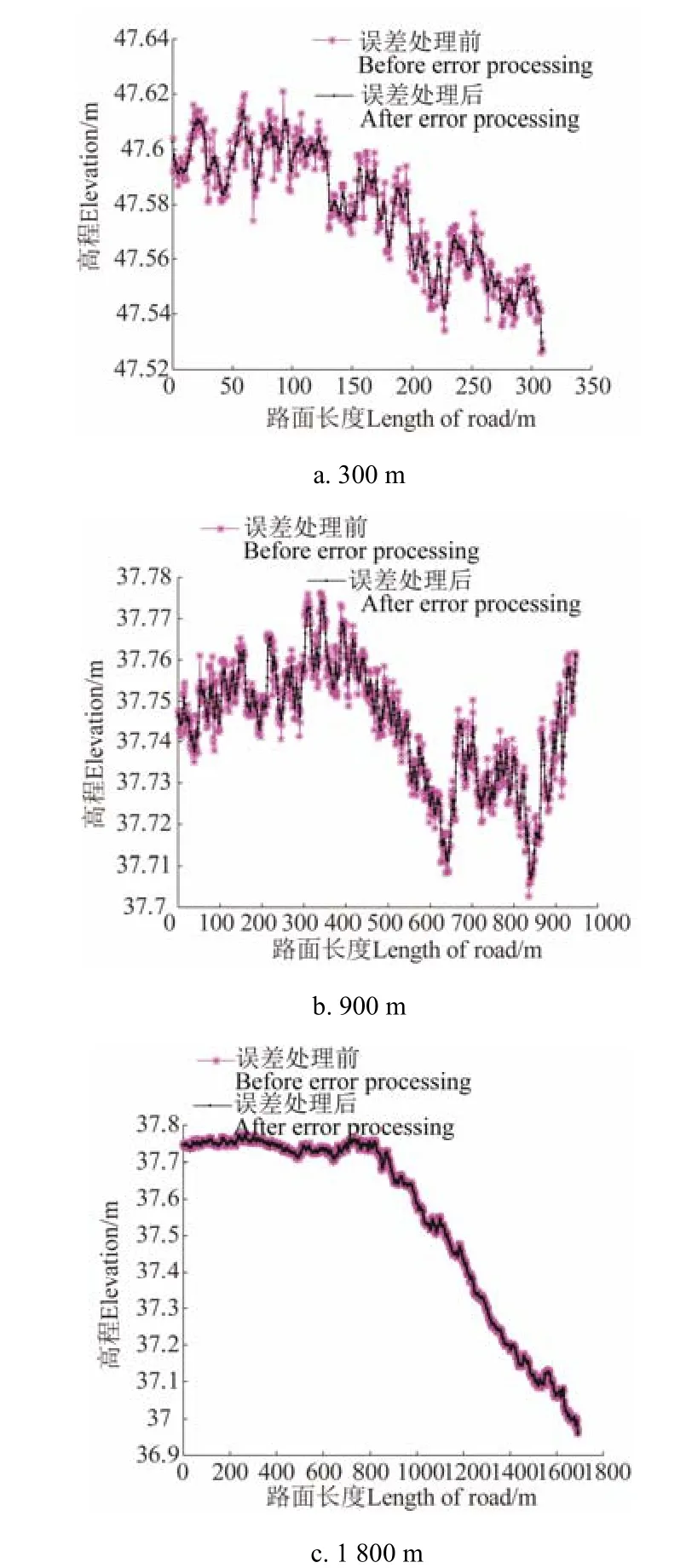
图4 不同长度路径下定向天线位置解算和误差处理前后的高程测量结果 Fig.4 Elevation measurement result of directional antenna before and after position calculation and error processing for different length road

由图4 可知，在水泥路面行驶过程中由于拖拉机启动带动平地铲发生机械振动，定向天线所测得的高程信息上下浮动。结合表1 可知，300 和900 m 路面长度的地形起伏较小，路面较平坦。定位天线经过误差处理后的误差和分别为1.986 和2.063 m，数据波动范围分别减小了4.67%和9.57%；定向天线经过误差处理后的误差和分别下降了1.909 和2.143 m，数据波动范围分别减小了8.42%和8.22%。当路面长度为1 800 m 时，数据采集时间更长，系统所处地形起伏较大，经过处理后定位天线的误差和为5.228 m，数据波动范围减小了1.52%；定向天线的误差和为5.956 m，数据波动减小了1.1%。测试结果证明本文的方法可以有效获取GNSS 双天线的位置信息，使定位精度得到较好的改善。

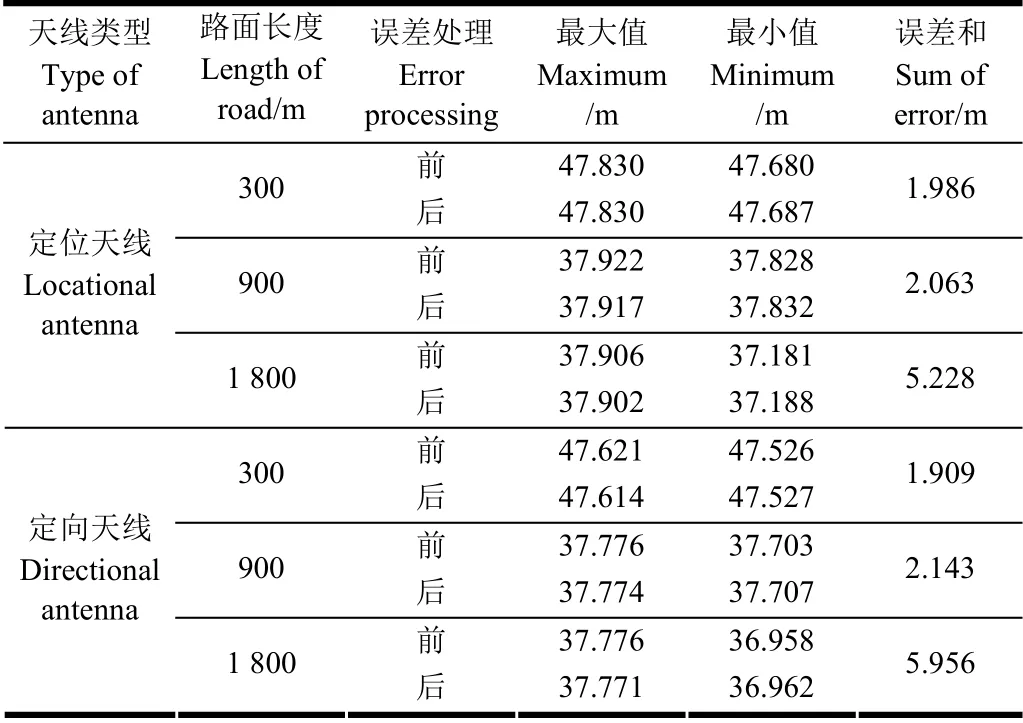
表1 定位、定向天线的高程测量结果 Table 1 Elevation measurement results of positioning and directional antenna on cement road

3.2 农田试验与结果分析

为进一步验证在农田地形起伏环境下，农田地形测量和误差处理方法的效果，选用中国农业大学上庄试验站的3 块农田进行标准区域划分[28-30]，并手动测量农田的地势信息。将手持GNSS 测量的地势信息作为真值，单天线测量的地势信息作为对照，与GNSS 双天线/AHRS 地形测量系统的测量结果进行对比。

首先将拖拉机启动并停至农田中，如图5 所示，AHRS 固定在至铲车顶部，设定采集频率为5 Hz（适合农田平整作业平地铲的最佳频率）。分别在5、15 和 30 min 内获取AHRS 测得的垂直方向加速度、航向角、俯仰角和翻滚角等主要信息，以验证AHRS 在农田环境下的测量精度，具体的试验结果如表2。

图5 AHRS 精度标定 Fig.5 Precision calibration of AHRS

表2 AHRS 精度标定结果 Table 2 Precision calibration result of AHRS

由表2 中可知，系统在农田环境下虽然受系统结构和地形的影响，随着测量时间增加至30 min，AHRS 获取的主要信息波动范围减小。结合表2 中数据可知，AHR 垂直加速度的均方根误差（root mean square error, RMSE）小于0.256 m/s²，航向角、俯仰角和翻滚角的均方根误差分别为0.903°、0.849°和0.531°，将误差角度带入式（4）中的空间位置方程，计算可知 |LsinθP| ≤2.9 cm（测量可得双天线之间的距离L=2 m），对GNSS 天线的测量结果影响较小，证明文中所选的AHRS可应用于复杂农田环境下的地形测量。

农田地形测量试验分为2 个部分：

1）机载地形测量试验。选取3 块未被耕作的农田，面积分别为35 m×50 m、35 m×100 m 和35 m×200 m。为保证GNSS 定位数据尽可能地遍历整个农田并结合平台自身体积影响，如图6a所示，将每块试验田划分成宽5 m的7 个区域。试验人员驾驶拖拉机分别使用GNSS 双天线/AHRS地形测量系统和单天线GNSS智能农田平整系统以1.12 m/s 的速度依次驶过这些区域，采集频率5 Hz，系统每次采用地头转弯的方式驶入下一个区域。

2）真实地势信息采集试验。如图6b 所示，真实地势信息由试验人员手持GNSS 卫星定位天线对试验农田进行测量。通过手持装有GNSS 定位天线的加长杆，沿着拖拉机行驶的路径每隔20 cm进行定点测量，3 块农田中分别采集到3 500、7 000 和14 000 个点（与单、双天线采集频率相对应）。由于机载地形测量平台的双天线测量路径对应平地铲车轮行驶路径，人工测量时GNSS 的数据采集路径与机载测量的14 条路径重合，以保证对比试验的可靠性。

图6 农田地形测量试验 Fig.6 Field topographic survey test

将不同测量方式得到的地势信息通过反距离加权（inverse distance weighting, IDW）插值法制图，结果如图7 所示。采用平整度、最大高程差和高程分布列[31-33]对测量结果进行评价，结果如表3 所示。

由图7 可以看出，原始单天线测量系统测量得到的三维地形图较为粗糙，双天线地形测量系统得到的地形图更为光滑，且更接近手持测量的真实地势信息。结合表3可知，经过位置方程解算得到的定位天线、定向天线的采集点数是单天线采集点数量的2 倍。相比于单天线，在3 块不同面积农田中，双天线系统测量得到的农田平整度分别由3.4 cm 下降到3.0 cm，由5.3 cm 上升到6.2 cm，由10.6 cm 上升到11.8 cm，与真值的平整度相比，准确性分别提高了14.286%、14.063%和10.084%；最大高程差分别由18.1 cm 下降到16.7 cm，由27.6 cm 下降到25.6 cm，由54.8 cm 下降到50.2 cm，与真值的最大高程差相比，准确性分别提高了8.642%、8.333%和8.897%；高差分布列分别由90.532%下降到85.650%，由55.677%下降到50.916%，由27.015%下降到24.024%，与真值的高差分布列相比，准确性分别提高了 1.536%、3.357%和2.991%。试验结果表明，双天线地形测量系统得到的地势信息更接近真值，地形测量精度高于单天线测量。

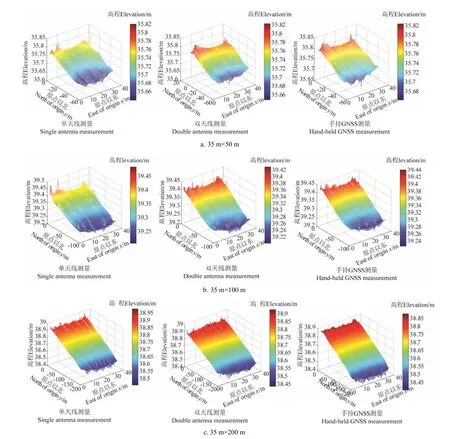
图7 不同测量方式的地形测量结果对比 Fig. 7 Comparison of topographic survey results with different methods

表3 手持GNSS、单天线和双天线的方式测量3 块农田的地势信息 Table 3 Topography information of three farmland measured by hand-held GNSS , single antenna and dual antenna

4 结 论

1）建立了基于GNSS 农田平整系统的双天线位置解算方程，在农田平整作业过程中可以有效的解算出定位、定向天线的位置信息。

2）提出了农田地势信息误差处理方法。本文通过分析地形测量时误差信号的来源和性质，以高精度AHRS为载体获取平地铲的姿态和加速度信号。利用最小二乘法对振动加速度进行预处理、快速傅里叶变换进行误差位移转换；五点三次法进行数据平滑处理，提高了GNSS 天线获取数据的光滑度和准确度。

3）进行了水泥路面和田间测量试验，试验过程中拖拉机的行驶速度为1.12 m/s。水泥路面的试验结果表明，双天线位置解算方程在动态环境下可以获得定位天线与定向天线的位置信息。经过误差处理后定位天线的数据波动最大可减少9.57%，定向天线的数据波动最大可减少8.42%，适用于基于GNSS 的农田平整作业。田间测量试验结果表明，农田环境中AHRS垂直加速度的均方根误差为0.256 m/s²，航向角、俯仰角和翻滚角的均方根误差分别为0.903°、0.849°和0.531°。与传统单天线农田地形测量方法对比，3 种地块面积（35 m×50 m、35 m×100 m 和35 m×200 m）下，双天线测量的农田平整度准确性分别提高了14.286%、14.063%和10.084%；最大高程差的准确性分别提高了8.642%、8.333%和8.897%。高差分布列的准确性分别提高了1.536%、3.357%和2.991%。双天线地形测量系统可以应用于精细农业中的地形测量，可为GNSS 农田平整作业提供精度高、持续稳定的农田地势信息。