电容器高频振动分析与结构优化

舒启佳 伍权 张麟 潘齐凤 王五松 田东斌

关键词： 非固体钽电容器; 高频振动; 有限元分析; 失效形式; 结构优化; 仿真分析

中图分类号： TN712+.3?34                        文献标识码： A                     文章编号： 1004?373X（2019）04?0037?05

High frequency vibration analysis and structure optimization of capacitors

SHU Qijia1， WU Quan1， ZHANG Lin2， PAN Qifeng2， WANG Wusong2， TIAN Dongbin2

（1. School of Mechanical and Electrical Engineering， Guizhou Normal University， Guiyang 550025， China;

2. China Zhenhua Xinyun Electronic Components Group Co.， Ltd.， Guiyang 550018， China）

Abstract： In allusion to the physical structure failure problem of non?solid tantalum capacitors in the high?frequency vibration environment， the high?frequency vibration simulation analysis is carried out by using the COMSOL Multiphysics software. The dynamic response features for internal stress and strain of the tantalum capacitor in the high?frequency vibration condition are researched. The failure mode of the capacitor is analyzed. The optimization design and experimental verification of the capacitor structure are conducted. The research results show that the internal stress of the tantalum capacitor is mainly concentrated at the contact point of the anode block， anode lead and adjusting gasket during the vibration process， and the maximum stress rises rapidly with the increase of the vibration acceleration， which can cause fracture failure. Therefore， a new claw?type gasket structure is designed to improve the structural reliability of the capacitor. The results of the finite element analysis and vibration test show that the operational reliability of the optimized tantalum capacitor in the high?frequency vibration environment is significantly improved.

Keywords： non?solid tantalum capacitor; high?frequency vibration; finite element analysis; failure mode; structure optimization; simulation analysis

0  引  言

钽电容器因体积小、功能稳定、准确度高成为整机最为基础和重要的电子元件之一，在军事、航天、仪器仪表等领域得到了广泛的应用[1?2]。强烈的振动会对钽电容器的结构与性能造成严重影响，甚至是物理失效，如阳极引线断裂、阳极块损坏、接触不良、脱焊等[3?4]。为确保钽电容器在强烈振动环境中性能与结构的稳定性，国内外生产厂家往往需要利用振动试验台对其进行高频振动试验[5]。但非固体钽电容器的小体积和特殊的成品封装形式，导致很难在高频振动的过程中利用位移传感器、动态应变仪等外部仪器获取内部结构的应力、应变等动态响应特性，使其结构的耐振性、可靠性和完好性测试受到限制[6]。

随着计算机技术和计算方法的发展，计算机仿真已在工程设计和科研领域得到了越来越广泛的重视和应用，成为解决复杂工程分析计算问题的有效途径[7?8]。杨文芳等人利用有限元分析得到了机载设备不同部位的响应和激励频带范围内的危险频率，并据此进行了系统的减振设计[9]。孙炜等人建立了插装型电子元器件的有限元模型，对其进行动态响应分析，揭示了元器件振动失效的原因[10]。

本文针对钽电容器高频振动时的失效问题，采用COMSOL Multiphysics有限元软件对非固体钽电容器进行高频振动仿真模拟，探索振动过程中电容器内部应力、应变等动态响应变化规律与特性，对电容器结构进行优化设计。该方法可以弥补传统振动试验台的局限性，节省试验成本与时间，为元件结构设计、优化、制造以及在振动环境中的应用提供有益的参考。

1  钽电容器有限元建模

钽电容器的结构较为复杂，主要由前塞柱、调整垫片、多孔介质阳极块、阳极引线、后塞柱和钽外壳组成，图1a）显示了一种非固体钽电容器的典型结构。模型的建立是有限元分析的关键，既要保证计算精度，又要考虑计算效率。因此，需要对钽电容器的物理模型、几何结构、边界条件进行适当的简化。在利用COMSOL Multiphysics对钽电容器进行有限元建模的过程中，忽略滚压圈对结构的影响，将与钽外壳直接接触的零件以固定关节副连接，阳极引线与阳极块以固定关节副连接，阳极引线与前塞柱、调整垫片以圆柱副连接。采用自由四面体网格进行自动划分，并在调整垫片与阳极块以接触副连接的地方进行网格加密，对于直径较细的阳极引线也进行网格加密，得到的非固体钽电容器半剖有限元模型如图1b）所示。

2  钽电容器高频振动分析

依据电子及电气元件试验方法中高频振动试验（GJB360B—2009）对钽电容器进行高频振动分析，采用正弦振动来确定元件的振型，分析其对结构和性能的影响。高频范圍内通常用振动加速度表征部件所受冲击力的强度，正弦位移函数为：

[S=Asin（2πft）] （1）

式中：A和f分别代表振幅和振动频率;t表示时间。振幅A和振动频率f共同决定振动加速度：[a=A（2πf）2]。因此，在该非固体钽电容器高频振动模拟中，将按照国军标，在10～80 g振动加速度范围内对阳极引线直径0.5 mm，0.8 mm，1.0 mm的钽电容器分别进行高频振动模拟。

2.1  钽电容器应力应变分布

有限元分析结果表明：调整垫片、阳极块、阳极引线三者接触处存在应力集中，且最大应力分布在阳极引线与阳极块过渡处，如图2a）所示。由于阳极块端面与调整垫片接触连接，而阳极引线受到塞柱的约束，高频振动时此位置存在较大的相对位移，导致应力集中的产生。应变主要集中在前后塞柱和调整垫片上，如图2b）所示。其主要是因为此部分零件的材质为聚四氟乙烯（PTFE），振动时比金属容易产生变形。同时，不管模拟参数如何变化，钽电容器在高频振动条件下其内部应力、应变皆呈相似的分布状态。

2.2  振动加速度对电容器结构稳定性的影响

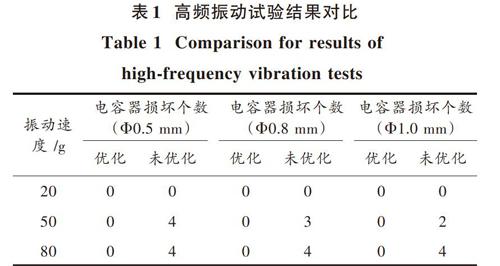
图3显示了阳极引线直径为0.5 mm，0.8 mm，1.0 mm的钽电容器在不同振动加速度条件下其内部最大应力的变化趋势。可以看出，随着振动加速度的增加，电容器内最大应力均迅速增加，且阳极引线直径0.5 mm的钽电容器受到的应力最大，在振动加速度由10 g增加到80 g的过程中，其电容器内部最大应力约从70 MPa增加到980 MPa。

为了解钽电容器在高速振动条件下的动态响应，分析了阳极引线直径0.5 mm（Φd=0.5）的钽电容器在20 g，50 g，80 g振动加速度下电容器内最大应力变化情况，其应力时程曲线如图4所示。

从图4可以发现，在不同振动加速度条件下，随着钽电容器做正弦振动，其内部最大应力值总体变化也呈现类正弦趋势，振动加速度越高，其振动过程中的变幅应力幅值就越大，钽电容器就越容易发生结构破坏。在80 g（电子元器件高频振动检测的最高频率）振动加速度条件下，钽电容器内部变幅应力幅值高达近1 000 MPa。

2.3  钽电容器失效分析

大量物理振动试验和实际使用过程中发现，该非固体钽电容器的物理失效形式绝大多数都是阳极引线在阳极块和调整垫片的接触处发生断裂。同时，引线断裂处的阳极块上有裂纹产生，如图5所示。

钽电容器在制作过程中不同的零件采用不同的材料与工艺，阳极块采用电容器级钽粉通过粉末冶金的方法制作，具有一定的孔隙率（约30%～40%），而阳极引线是通过轧制、拉拔等塑性成形工艺制作而成的钽丝，其抗拉强度[11]为300（软态）/1 250（硬态）MPa。研究表明，在最小实体面模型中，多孔材料的力学性质与孔隙率呈指数关系。对于孔隙均匀、孔隙率在20%以上的多孔材料，其抗压强度与孔隙率之间满足以下关系[12?13]：

[σ=σ0e-cp] （2）

式中：σ与σ0分别表示多孔材料与致密材料的抗压强度;p表示多孔材料的孔隙率;c为与孔洞性质有关的经验系数。由此可见，多孔阳极块的强度小于钽丝的强度。高频振动仿真结果表明，振动过程中最大应力集中在阳极引线和阳极块的过渡处。因此，钽电容器振动时会在阳极引线周围的阳极块上最先出现裂纹，且随着振动的持续，裂纹不断扩展可能导致阳极块发生破坏。同时，阳极引线在振动时承受了交变循环应力，当振动时间过长或振动剧烈时容易发生断裂失效。随着振动加速度的增加，钽电容器内的应力迅速增大，钽电容器发生结构失效的可能性增加。

3  钽电容器结构优化

钽电容器的振动属于阻尼受迫振动。振动分析主要是考察系统对激励的响应。图6为受迫振动系统的简化模型。

激振力[F=F0sin ωt]，其中F0为最大激振力，[ω]为激振力的圆频率。以平衡位置为坐标原点，则运动的微分方程可写为：

[y+2ξωy+ω2y=Fmsin θt]  （3）

设特解为[y=Asin θt+Bcos θt]，齐次解加特解得到通解：

[y=y1+y2=e-ξωt（C1cos ωrt+C2sin ωrt）+                         Asin θt+Bcos θt] （4）

式中：

[y1=e-ξωtC1cos ωrt+C2sin ωrt] （5）

[y2=Asin θt+Bcos θt=ypsinθt-α] （6）

[α=arctan2ξθω1-θω2] （7）

[yp=A2+B2=yst1-θ2ω22+4ξ2θ2ω2-1/2] （8）

[yst=Fk=Fmω2] （9）

式中：α為相位角;yp为振幅;yst为最大静力位移。式（4）是两部分的和，右端第一项y1为阻尼衰减振动，经过短暂时间迅速衰减，称瞬态响应，最后得到y2持续等幅振动，称稳态响应，即系统的稳态受迫振动。由受迫振动系统的微分方程可知，ξ和ξ2分别处在y1的指数衰减和受迫稳态振幅yp的分母位置，因此增大阻尼比ξ将会有效地抑制瞬态衰减的最大位移和减小稳态振幅，从而减小振动过程中的形变。

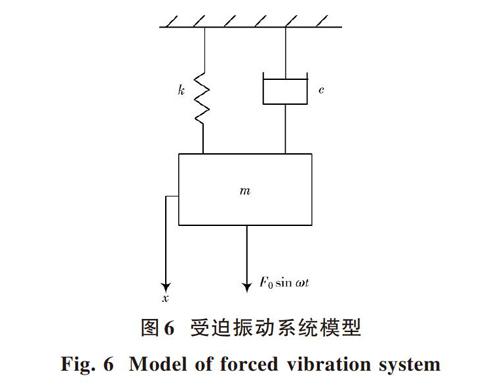
从阻尼受迫振动的角度来分析钽电容器的高频振动：烧结在一起的阳极引线和阳极块作为受迫振动的质量振子，要达到减小阳极引线和阳极块在振动过程中的应力集中，增大阻尼比ξ将会有效地减小瞬态衰减和稳态振动时阳极引线和阳极块的形变，从而减少振动过程中的应力集中以提高其结构稳定性。因此从加大系统阻尼（摩擦阻尼、约束阻尼等）的角度出发[14?15]，设计一种新型爪式垫片结构，以限制阳极块的移动错位、增大阳极块和与之相连的阳极引线的约束阻尼，从而达到降低阳极引线和阳极块上的集中应力的目的如图7所示。对采用新型爪式调整垫片的钽电容器在80 g振动加速度条件下进行高频振动模拟仿真（阳极引线直径为0.5 mm），并将其与未改进的钽电容器的应力响应过程进行对比，如图8所示。

从应力时程曲线对比图中可以发现，采用新型爪式调整垫片的钽电容器在80 g振动加速度下变幅应力幅值约为43 MPa，且呈现出较为平缓的变化趋势，垫片未做改进的则约为980 MPa。仿真结果表明，新型爪式调整垫片能够显著地降低钽电容器内部的变幅循环应力幅值，减小应力集中现象。

为了验证新型垫片对提高钽电容器结构稳定性的效果，制作了一批采用新型爪式调整垫片的钽电容器。与未做优化的钽电容器进行高频振动对比试验（每组试验下，优化和未做优化的电容器数量均为4），并依据GJB360B—2009《电子元器件高频振动试验条件》，在ES?80?445型电磁振动试验平台进行高频振动对比物理试验，如图9所示。

对比振动试验结果表明：采用优化结构的钽电容器（引线直径为0.5 mm，0.8 mm，1.0 mm）在高频振动试验下均未发生损坏，其高频振动环境下的工作稳定性与可靠性得到了显著提高。而未做优化的钽电容器在20 g振动加速度以上，其阳极引线和阳极块皆有不同程度的损坏，具体结果如表1所示。

4  结  论

钽电容器的高频振动过程是一个非常复杂的过程，结构与振动参数的变化都会对其产生较大的影响。通过基于COMSOL Multiphysics有限元软件的高频振动仿真和物理振动试验，得出以下结论：

1） 高频振动过程中，钽电容器内部应力主要集中于阳极块、阳极引线、调整垫片三者接触处，最大应力随着振动加速度的提高而迅速上升。阳极引线与阳极块因应力集中易发生结构破坏。

2） 采用新型爪式调整垫片可以有效地减小高频振动过程中电容器内部应力变化幅值，能够显著地提高钽电容器在振动环境下的结构稳定性与可靠性，具有较好的工程价值。

参考文献

[1] 田东斌，张强，张选红，等.有机固体电解质钽电容器的失效机理及预防措施[J].电子元件与材料，2015，34（5）：23?26.

TIAN Dongbin， ZHANG Qiang， ZHANG Xuanhong， et al. Failure mechanism and preventive measures of the organic solid electrolyte tantalum capacitors [J]. Electronic components & materials， 2015， 34（5）： 23?26.

[2] FREEMAN Y， ALAPATT G F， HARRELL W R， et al. Asymmetric conduction and stability of polymer tantalum capacitors [J]. ECS journal of solid state science and technology， 2015， 4（7）： 70?75.

[3] 张晓英.一种受迫振动系统的自动测控方法[J].现代电子技术，2008，31（23）：120?121.

ZHANG Xiaoying. Auto?measuring and control method of forced vibrating system [J]. Modern electronics technique， 2008， 31（23）： 120?121.

[4] 陶帅，胡小海.型号设备用钽电解电容器可靠性研究[J].电子产品可靠性与环境试验，2018，36（1）：34?38.

TAO Shuai， HU xiaohai. Research on the reliability of tantalum electrolytic capacitor for equipments [J]. Electronic product reliability and environmental testing， 2018， 36（1）： 34?38.

[5] PAVELKA J， SIKULA J， VASINA P， et al. Noise and transport characterisation of tantalum capacitors [J]. Microelectronics reliability， 2002， 42（6）： 841?847.

[6] 鄢波，方鸣，张选红，等.非固体电解质230 ℃高温全钽电容器制造技术的研究[J].材料导报，2013，27（S1）：160?163.

YAN Bo， FANG Ming， ZHANG Xuanhong， et al. Studies on manufacturing technology of wet all tantalum capacitors with high temperature capability to 230℃ [J]. Materials review， 2013， 27（S1）： 160?163.

[7] 范文慧，吴佳惠.计算机仿真发展现状及未来的量子计算机仿真[J].系统仿真学报，2017，29（6）：1161?1167.

FAN Wenhui， WU Jiahui. Development and future trend of computer simulation and quantum computer simulation [J]. Journal of system simulation， 2017， 29（6）： 1161?1167.

[8] 郝腾飞，李军锋，李晓莹，等.三维虚拟仿真技术在电力设备设计中的应用[J].现代电子技术，2018，41（14）：51?54.

HAO Tengfei， LI Junfeng， LI Xiaoying， et al. Application of 3D virtual simulation technology in power equipment design [J]. Modern electronics technique， 2018， 41（14）： 51?54.

[9] 杨文芳，魏强，朱兰琴.基于有限元分析的机载电子设备减振设计[J].振动与冲击，2010，29（5）：230?234.

YANG Wenfang， WEI Qiang， ZHU Lanqin. Anti?vibration design for an airborne electronic equipment based on finite element method [J]. Journal of vibration and shock， 2010， 29（5）： 230?234.

[10] 孙炜.插装型电子元器件强化振动试验疲劳仿真研究[D].长沙：国防科技大学，2003.

SUN Wei. Vibration fatigue simulation research on through?hole electronic component in RET [D]. Changsha： National University of Defense Technology， 2003.

[11] 宁夏东方钽业股份有限公司.钽系列[EB/OL].[2018?02?13].http：//www.otic.com.cn/index.php？m=content&c=index&a=show&catid=114&id=3.

Ningxia Orient Tantalum Industry Co.， Ltd. Tantalum series [EB/OL]. [2018?02?13]. http：//www.otic.com.cn/index.php？m=content&c=index&a=show&catid=114&id=3.

[12] LU G， LU G Q， XIAO Z M. Mechanical properties of porous materials [J]. Journal of porous materials， 1999， 6（4）： 359?368.

[13] RICE R W. Limitations of pore?stress concentrations on the mechanical properties of porous materials [J]. Journal of materials science， 1997， 32（17）： 4731?4736.

[14] JI J C， ZHANG N. Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber [J]. Journal of sound and vibration， 2010， 329（11）： 2044?2056.

[15] 杜全忠，王鹏，王旭明，等.受迫振动的阻尼特性研究[J].实验室研究与探索，2015，34（11）：14?17.

DU Quanzhong， WANG Peng， WANG Xuming， et al. Research by forced vibration of damping characteristics [J]. Research and exploration in laboratory， 2015， 34（11）： 14?17.