基于有理函数模型的北京二号影像几何校正

王 超，吴亚文，张 伟

（1.重庆师范大学地理与旅游学院，重庆 400047；2.宁波市阿拉图数字科技中心，浙江 宁波 315042； 3.宁波市测绘设计研究院，浙江 宁波 315042）

遥感卫星是人们对地观测，获取地理空间信息和地球信息资源的重要技术手段之一。随着航天技术的发展，以遥感卫星为核心技术的高分辨率对地观测能力有了巨大的进步，在土地利用监测、城市规划建设、农业、林业以及自然灾害等方面起到了重要作用，极大地满足社会各个方面的需求[1]。然而，在成像过程中，高分辨率遥感卫星影像受到地球自转、大气折光、卫星姿态变化等因素的影响，产生了不同程度的旋转、平移、缩放等几何畸变，不利于后续的应用，因此需要对影像进行几何校正。

长期以来，遥感影像的几何校正主要是根据控制点采用多项式拟合的方法，前提是需要提供量多且分布均匀的地面控制点。而在海洋、沙漠、无人区、境外等区域，由于缺少地理信息控制，人员无法实时实地操作定点，导致地面的控制点难以获取[2-3]。因此,研究如何对缺少地面控制点的影像进行几何校正是当前的热点。例如，张过基于有理函数模型的高分辨率遥感影像区域网平差，补偿不同立体模型系统误差间的差异，能极大提高缺少控制点的测图精度，但沿轨道方向的系统误差仍比较明显[4]；Grodecki 分析了有理函数参数误差来源，利用仿射变换模型补偿有理函数模型误差[5]；晏杨提出的基于像平面坐标的二维直接线性变换的快速正射纠正方法，减小了影像正射纠正的计算量,提高了校正速度和效率[6]；杨国东采用有理函数模型与DEM 结合的方式进行正射校正，在地面控制点数量有限的情况下，对有理函数模型参数进行纠正，使道路和建筑物图像轮廓有了有效变化[7]；姚星辉提出的多重观测卫星影像的无控区域网平差方法，基于“单物方—多像方”的连接点建立，与其他区域网平差相比，该方法明显提高了遥感影像的绝对定位精度[8]。

1 卫星影像的几何校正原理

1.1 几何校正定义

几何校正一般利用一系列数学模型来消减或消除遥感影像成像时产生的几何畸变，获得更高精度的遥感影像[9]。方法主要包括系统校正、多项式校正法、基于有理函数模型的几何校正法等。其中，系统校正主要根据传感器参数和姿态参数等，由于传感器参数的保密性，其通用性不高，而基于有理函数模型的几何精校正通过建立严格的几何模型生成量多且均匀的控制点，引入较多定向参数，模拟精度更高，应用更灵活。

1.2 基于RPC 的有理函数模型

基于有理多项式系数（RPC，Rational Polynomial Coefficients） 的 有 理 函 数 模 型（RFM，Rational Function Model）相对于各种传感器几何模型其表达形式更精确、更普遍，但需利用误差补偿模型来补偿影像的RPC 参数误差[10-11]。RFM 是把影像坐标p（r，c） 与地面坐标P（X，Y，Z）关联起来，建立比值多项式的数学关系，其表达形式如下[4]：

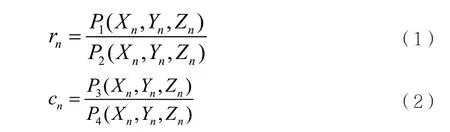
式中，P（X，Y，Z）为多项式函数，其每项的X、Y、Z的幂最大为3，每项的X、Y、Z的幂值总和也不高于3，通常取值为1、2、3 三种。具体表达式如下：

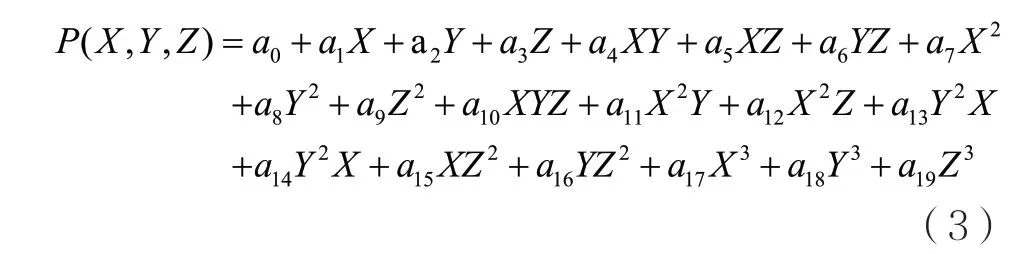
式中，a0，a1，a2，……，a19是有理函数的系数。

在计算中，由于数据量级别间存在的差距，往往会产生舍入误差，因此，为了维持计算过程的稳定，减少该误差，需将影像坐标（r，c）和地面坐标 （X，Y，Z）经过缩放和平移的正则化，得到值范围在（-1，1）之间的标准化坐标，变换形式如下：

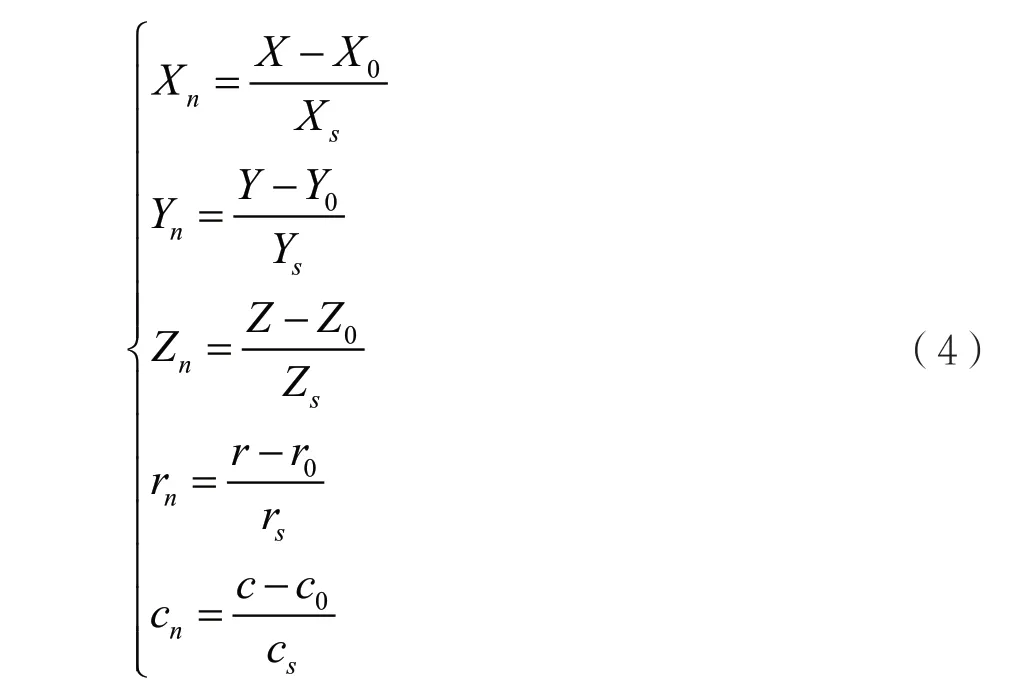
式中，（X0，Y0，Z0，r0，c0）是标准化平移参数；（Xs，Ys，Zs，rs，cs）为标准化比例参数。

2 几何校正试验

2.1 试验数据

本次试验的研究区位于浙江省宁波市，地处平地地区，长江三角洲南翼，市区海拔4.0～5.8 m，郊区海拔3.6～4.0 m，地势相对平坦。试验通过选取2018年3月10日采集的北京二号遥感卫星影像数据，采用该影像数据中的高分辨率全色和多光谱数据，结合相同范围的DEM 数据进行几何校正。

2.2 试验过程与结果

本次试验研究了基于北京二号的RPC 模型的几何校正、控制点个数与纠正精度的关系以及研究区地势对控制点分布的影响。

首先，将试验数据利用有理函数模型进行几何纠正处理。然后，采用仿射变换模型，应用不同数量的控制点（见图1），主要包括分布均匀的21 组试验分布情况，统计控制点中误差（见表1）和折线图（见图2），分析控制点数量影响下的变化趋势。最后，通过最优性将选取具有代表性的16 个控制点作为下一步研究基础，结合遥感影像辨识控制点分布位置的地势，统计相对比例（见表2）。

图1 试验影像及部分不同数量的控制点分布

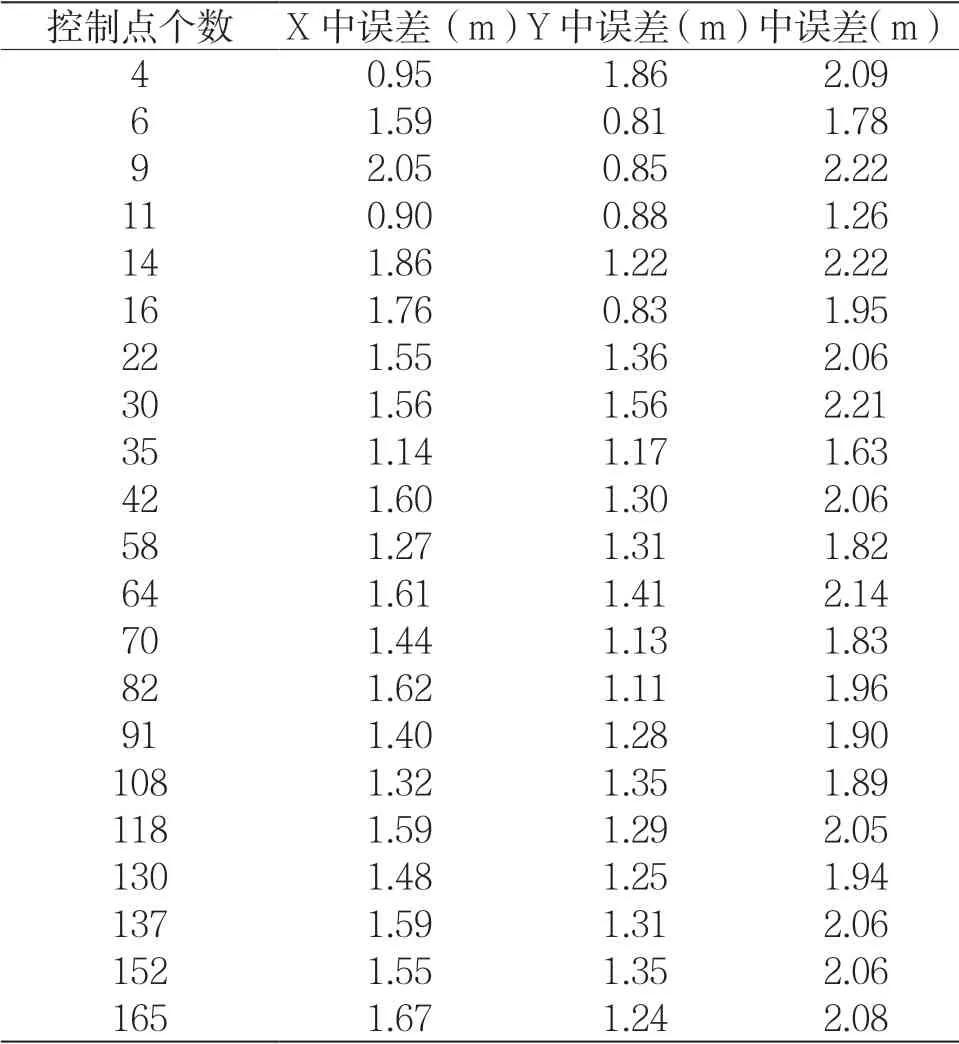
表1 不同数量控制点的中误差对比

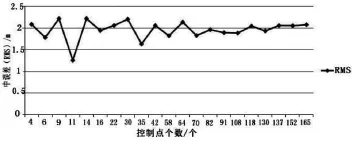
图2 不同数量控制点的中误差趋势图

表2 控制点分布的地势情况

2.3 试验结果分析

由本次试验结果可以看出，利用有理函数模型处理北京二号影像进行几何校正，其处理效果理想。

分别选取不同控制点数4、6、9、11……130、137、152、165，共21 组，结合试验区的DEM，根据表1和图2可知，随着控制点个数的增加，中误差的变化情况是在70 个点后逐渐趋于平缓，说明当控制点数量达到某一阈值时，平面中误差基本保持不变，几何精度的变化也趋于平缓。整体看来，平面平均中误差为1.96。其中，控制点个数为11 个时，达到最小中误差为1.26，控制点数量为9 或14 个，达到最大中误差为2.22。这说明控制点的数量会影响几何校正精度，因此，在选取控制点数量时，人们要根据实际情况进行，其必须均匀分布。

本次试验控制点分布的地势大致分为平地和山区，根据表2可直观得出，随着控制点选取数量的增多，当控制点个数达到70 后，控制点分别分布在平地和山区的数量比例逐渐保持不变，平地所占比例在80%～100%，山地比例小于20%。其中，从图2和表3可得，当控制点个数为6 时，控制点在平地与山地的分布比例相等，同时当控制点数量为11 时，山区比例为18%，平地比例为82%，此时平面中误差值最小为1.26，这是由于控制点地势位置的分布影响几何校正精度，控制点分布平地比例越高，山区分布比例越低，平面中误差越小，几何校正精度越高。由此可以得出，控制点在地势上的分布也会影响几何校正精度。

3 结论

随着空间技术的不断发展，遥感影像的使用越来越普及，人们对高分辨率影像的精度要求越来越严格。北京二号卫星作为民用商业遥感卫星，在国民经济、环境建设等方面提供着高分辨率的地理空间信息数据，对其影像校正的研究是有意义的，为其他研究提供了经验和意见。综上所述，本文基于有理函数几何校正试验，得出以下几点结论。

一是本次试验利用有理函数模型对北京二号影像进行几何校正，得到了理想的结果。当进行几何校正时，控制点数量达到某一阈值，校正的精度相对保持不变，因此对控制点数量的选取要根据实际情况，择优不择多。二是控制点的地势分布会影响平面中误差的大小，导致几何校正的精度不同。在基于控制点均匀分布的前提下，平地控制点分布越多，中误差越小，相对校正精度会越高，更有利于影像的后期使用。另外，本次试验仍有些许不足，在进行控制点地势分析时，主要采用人工目视解译的方法，在地势判断上会有些许偏差，在以后的研究工作中还需进一步改正。