基于PSO-RBF神经网络的海战场电磁态势预测

杨洁 程晓健 穆彦斌

關键词： 海战场; 电磁态势; 神经网络; 粒子群算法; 模拟退火法; 遗传算法

中图分类号： TN911.1?34; TP311.54                   文献标识码： A                文章编号： 1004?373X（2019）03?0001?05

Abstract： A sea battlefield electromagnetic state prediction method based on improved particle swarm optimization （PSO）algorithm optimizing radial basis function （RBF） neural network is proposed to solve the prediction problem of sea battlefield electromagnetic state. The adaptive inertia weight， simulated annealing method and genetic algorithm are used in the method to improve the conventional PSO algorithm， and its search accuracy and speed. The improved PSO algorithm is used to optimize the parameters of RBF neural network， which can improve the learning efficiency and prediction accuracy of the network. The simulation prediction is carried out for the non?linear mapping relationship between the electromagnetic state values of the sea battlefield. The experimental results show that the method can improve the prediction accuracy of the sea battlefield electromagnetic state effectively， and has strong applicability.

Keywords： sea battlefield; electromagnetic state; neural network; particle swarm optimization algorithm; simulated annealing method; genetic algorithm

0  引  言

海战场电磁态势感知是一种通过对海战场电磁环境要素的获取、理解、预测而形成易于指挥员准确认识海战场电磁环境并能辅助其决策的方法[1]。现有的态势评估方法大多只能提供给指挥员过去和当前的海战场电磁态势情况，无法预测下一阶段态势变化情况，使得己方在未来战争中处于被动状态。因此，海战场电磁态势预测成为未来战场中亟待解决的问题。

目前国内外对于海战场电磁态势的研究主要集中在电磁环境可视化[2]、电磁环境复杂度评估[3]、辐射源识别[4]等方面，缺乏生成系统海战场电磁态势的技术手段。文献[1]提出了海战场电磁感知的基本模型，但并未对态势理解域中的态势预测作进一步分析。文献[5]将博弈论应用于战场通信对抗态势预测中，但预测结果误差较大。径向基函数（Radial Basis Function，RBF）神经网络具有收敛速度快、结构简单、非线性映射能力好等特点[6]，已广泛应用于模式识别[7]、网络安全态势预测[8]等领域。同时，为了提高RBF神经网络性能，国内学者利用粒子群算法（Particle Swarm Optimization，PSO）的搜索能力和RBF神经网络的非线性映射能力，提出改进粒子群算法优化RBF神经网络预测模型[9]。

为了准确把握海战场电磁发展态势，在已有研究成果的基础上，提出一种基于改进PSO算法优化RBF神经网络的海战场电磁态势预测方法。该方法首先对海战场电磁态势要素进行分析，继而获得海战场电磁整体态势值，然后采用改进的粒子群算法优化RBF神经网络，寻找海战场电磁值之间的非线性映射关系，对未来时刻海战场电磁态势进行预测。

1  海战场电磁态势预测框架

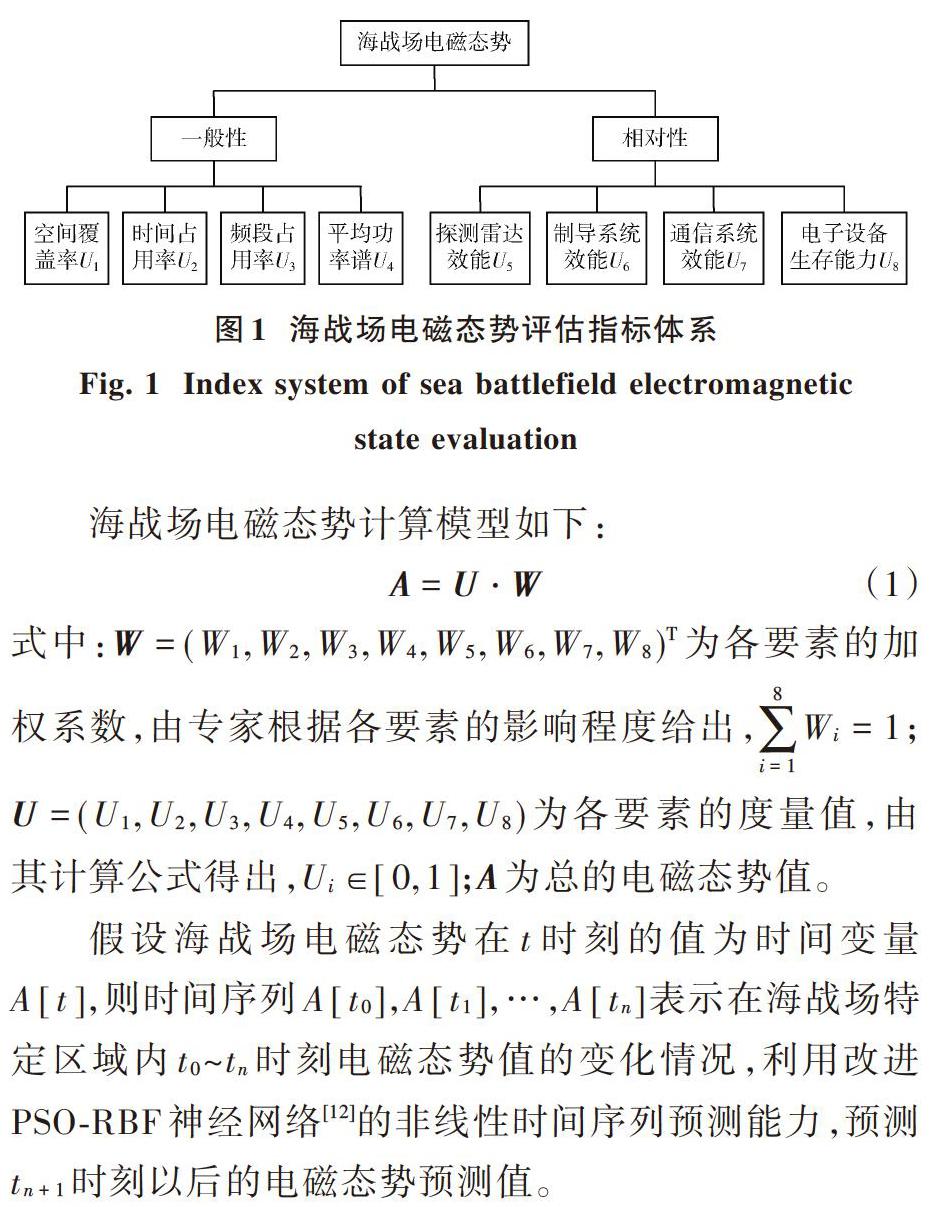
海战场电磁态势值是在对海战场电磁环境物理特性和电磁环境中电子设备用频效能分析的基础上，通过一定的数学模型进行计算，将人们不易理解的海战场电磁环境和战场态势信息归并融合成人们容易理解和接受的数值。这些数值能够客观实时反映海战场电磁域中战场态势情况，其大小取决于海战场电磁态势要素。针对电磁环境特点，将电磁态势划分为一般态势和相对态势两部分。一般态势如海战场区域内电磁信号的空间覆盖率、时间占用率、频段占用率、平均功率密度谱等[10];相对态势如探测雷达的发现目标概率和最大探测距离，制导系统对目标的跟踪精度和制导概率，通信系统之间的误信率、误码率以及电子设备和系统在电子干扰和反辐射攻击中的生存能力等[11]。电磁态势评估指标体系如图1所示。

同时为了验证所提算法的优越性，采用IMPSO?RBF预测模型[9]及SACPSO?RBF预测模型[12]进行相同的实验。网络训练过程中最优适应度值曲线如图3所示，预测结果如图4所示。

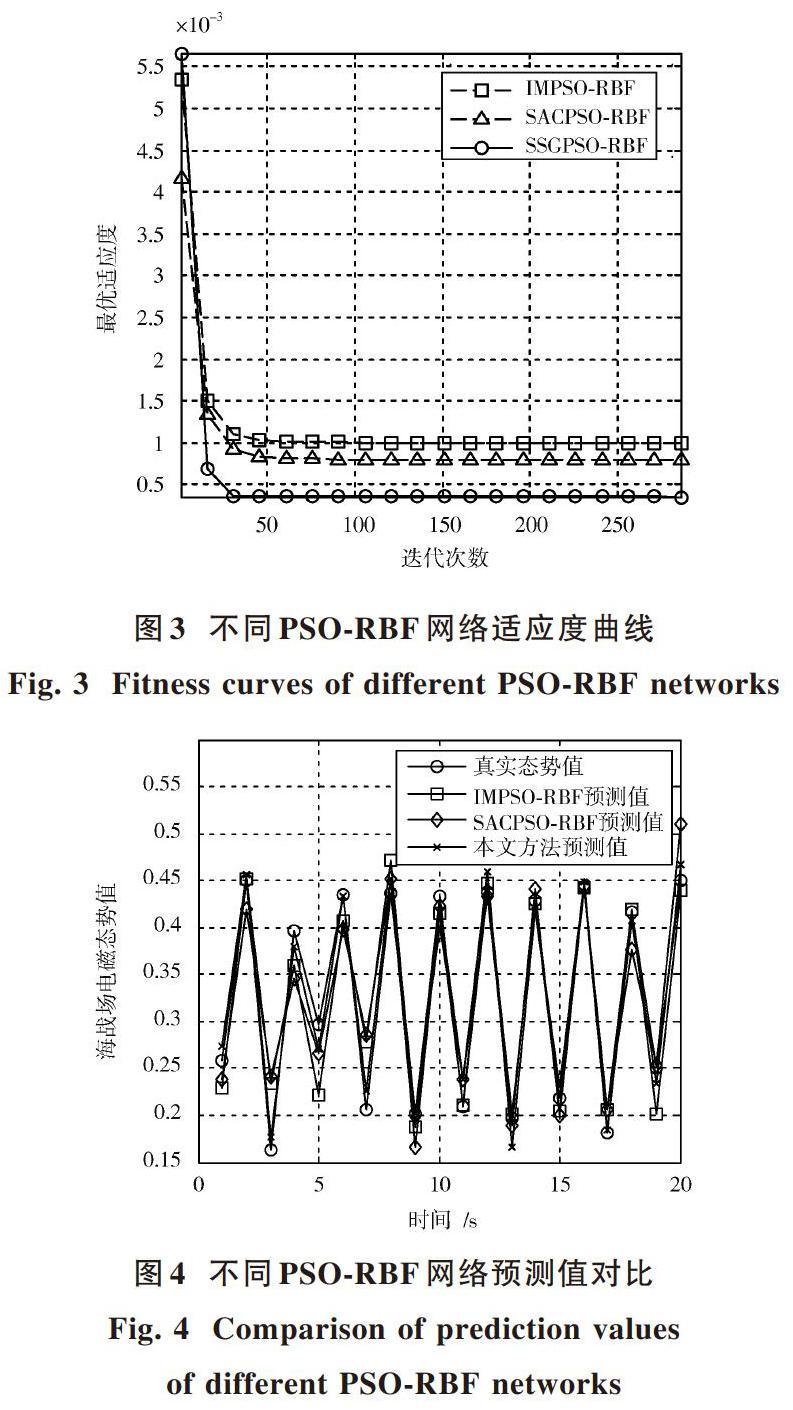
由图3所示，尽管三种预测模型在网络训练过程中最佳适应度值都可以很快收敛到最小值，但相对于其他两种预测模型，该预测模型可以更快找到态势值之间的非线性映射关系。其原因在于本文方法能够根据粒子群中粒子的适应度值自适应赋予其移动速度权重，能更快地寻找到最佳粒子位置，因此，加快了优化后的RBF网络预测模型的收敛速度。

由图4中的预测曲线可以看出，三种预测模型都取得了一定的预测效果。如图5所示，本文方法的预测效果更好，更符合真实电磁态势变化趋势。这是因为本文方法采用模拟退火法避免了粒子群算法在搜索过程中陷入局部极小值的问题，并采用遗传算法中的交叉、变异操作提高了种群多样性，提高了PSO算法在全局最优解的搜索能力。

为了进一步体现本文方法的优越性，分別计算了三种预测模型的均方根误差（RMSE）、平均相对误差（MAPE），如表1所示。

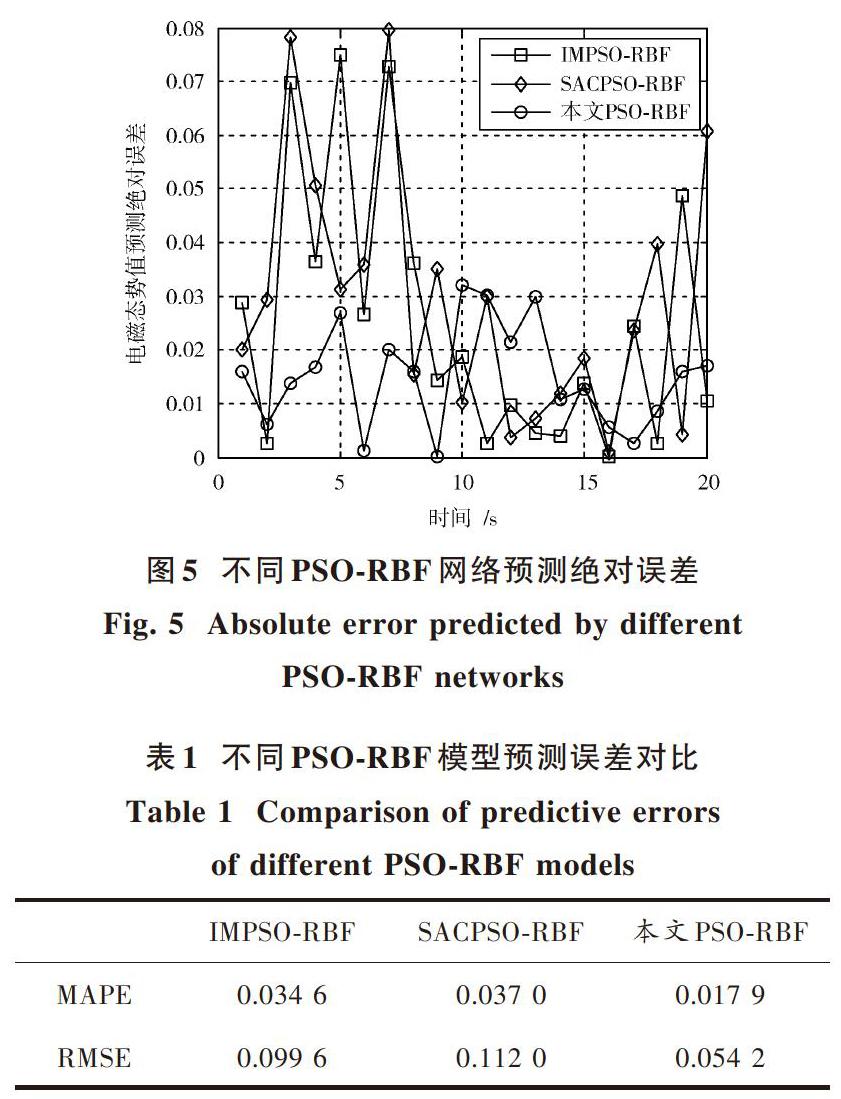
从表1中可以看出，相对于IMPSO?RBF预测模型及SACPSO?RBF预测模型，本文预测模型得到的电磁态势值的均方根误差（RMSE），平均相对误差（MAPE）均明显降低。

4  结  语

针对海战场电磁态势的预测问题，本文提出一种基于改进PSO优化RBF神经网络的海战场电磁态势预测方法。通过对海战场电磁态势要素的分析，生成能客观反映海战场电磁域的整体态势值，利用改进PSO算法优化RBF神经网络参数，并与其他预测模型的测试结果对比，该方法可以取得更高的预测精度，在海战场电磁态势预测领域具有一定的应用价值。

参考文献

[1] 周倜，王小非，陈炜.海战场电磁态势感知模型[J].火力与指挥控制，2013，38（8）：1?5.

ZHOU Ti， WANG Xiaofei， CHEN Wei. Electromagnetic situation perception model for sea battlefield [J]. Fire control & command control， 2013， 38（8）： 1?5.

[2] TANG D， HAN H， YUAN K. Research on the essence and visualization description method of battlefield electromagnetic environment [J]. Ordnance industry automation， 2014（11）： 57?59.

[3] WANG F， HAN H， WANG J， et al. The complexity evaluation method of electromagnetic environment based on statistical characteristics analysis [J]. Applied mechanics & materials， 2013， 321/324： 779?784.

[4] 陈求，戎华，谭亮亮.基于最小二乘法的雷达辐射源精确识别指标权重确定方法[J].舰船电子对抗，2016，39（4）：52?55.

CHEN Qiu， RONG Hua， TAN Liangliang. A method for determining precise identification indexes of radar emitters based on least squares [J]. Shipboard electronic countermeasure， 2016， 39（4）： 52?55.

[5] 冯德俊，朱江，李方伟.战场电磁态势感知关键技术研究[J].数字通信，2013，40（5）：20?23.

FENG Dejun， ZHU Jiang， LI Fangwei. Research on key technologies of electromagnetic situation sensing in battlefield [J]. Digital communication， 2013， 40（5）： 20?23.

[6] HAN H G， QIAO J F. Prediction of activated sludge bulking based on a self?organizing RBF neural network [J]. Journal of process control， 2012， 22（6）： 1103?1112.

[7] 杜刚，何朔，于海鹏.基于径向基函数神经网络的空间碎片撞击模式识别研究[J].航天器环境工程，2015，32（4）：357?360.

DU Gang， HE Shuo， YU Haipeng. Research on pattern recognition of space debris impact based on radial basis function neural network [J]. Spacecraft environment engineering， 2015， 32（4）： 357?360.

[8] 李方伟，郑波，朱江，等.一種基于AC?RBF神经网络的网络安全态势预测方法[J].重庆邮电大学学报（自然科学版），2014，26（5）：576?581.

LI Fangwei， ZHENG Bo， ZHU Jiang， et al. An approach to forecast the network security situation based on AC?RBF neural network [J]. Journal of Chongqing University of Posts and Telecommunications （natural science edition）， 2014， 26（5）： 576?581.

[9] 夏轩，许伟明.改进的粒子群算法对RBF神经网络的优化[J].计算机工程与应用，2012，48（5）：37?40.

XIA Xuan， XU Weiming. Optimization of RBF neural network based on improved particle swarm optimization [J]. Journal of computer engineering and applications， 2012， 48（5）： 37?40.

[10] CAI X F， SONG J S. Analysis of complexity in battlefield electromagnetic environment [C]// 2009 IEEE Conference on Industrial Electronics and Applications. Xian， China： IEEE， 2009： 2440?2442.

[11] 高波，马向玲，隋江波.海战复杂电磁环境分析[J].火力与指挥控制，2013，38（3）：1?4.

GAO Bo， MA Xiangling， SUI Jiangbo. Analysis of complex electromagnetic environment in sea battle [J]. Fire control & command control， 2013， 38（3）： 1?4.

[12] 张义，田爱奎，韩士元.一种自适应的混沌粒子群优化RBF神经网络算法[J].重庆理工大学学报，2015，29（11）：126?130.

ZHANG Yi， TIAN Aikui， HAN Shiyuan. An adaptive RBF neural network algorithm based on chaotic particle swarm optimization [J]. Journal of Chongqing Institute of Technology， 2015， 29（11）： 126?130.

[13] CHEN G C， YU J S. Particle swarm optimization algorithm [J]. Information & control， 2005， 306： 1369?1372.

[14] 董俊，洪丽娜，汪连栋，等.多辐射平台运动区域电磁环境预测方法[J].现代防御技术，2016，44（2）：190?196.

DONG Jun， HONG Lina， WANG Liandong， et al. An electromagnetic environment prediction method in multi?radiation platform motion area [J]. Modern defence technology， 2016， 44（2）： 190?196.