共振频率下油船液舱晃荡数值模拟研究

甄长文，吴文锋，朱柯壁，张建伟，卢金树

(浙江海洋大学 船舶与机电工程学院，浙江 舟山 316022)

液体晃荡是一种极为复杂的流体运动形式，它具有高度的非线性和随机性。油船在营运过程中，受海浪影响，舱内原油随船舶摇晃而发生晃荡，晃荡对液舱壁面产生的拍击压力可能会造成结构损坏，因此，有必要研究油船舱内原油的晃荡特征及预报舱壁晃荡压力的大小问题。

蔡忠华等[1]利用试验与数值模拟相结合的方法，探究共振频率下LNG船液舱晃荡的晃荡特征，其中液体选取的是水；张书谊等[2]利用Fluent软件探究了横荡激励条件下，二维矩形舱内不同水深与不同激励频率下自由液面的变化情况；刘文夫[3]等利用水做模型试验，研究了计及弹性支撑效应下刚性舱内液体的晃荡特征。上述学者研究了共振与非共振频率下液舱晃荡的特征，但液舱内液体采用水这种低黏流体，与油船液舱晃荡不相符。

本文在考虑共振频率下，结合RNG-k-ε与多相流模型，模拟油船舱内原油晃荡过程。通过分析自由液面波高历时曲线与左侧壁液面波动变化，以及不同点处的晃荡压力，得出油船舱内原油的晃荡特征。

1 数值模型

本文采用黏性流理论求解油船原油舱内非定常流体晃荡运动，采用有限体积法计算模拟晃荡流体的非线性现象。假设液舱为刚性舱，舱内流体为不可压缩黏性流体，同时假定流体在晃荡过程中始终保持温度不变。

1.1 控制方程

连续性方程：

(1)

动量方程：

(2)

式中：u、v、w分别为x、y、z方向上的速度分量，m/s；p为压力，Pa；ρ为流体密度，kg/m3；μ为运动黏度，mm2/s；t为时间，s；Fx、Fy、Fz分别为x、y、z方向上流体的单位质量力，N。

由于文中仅涉及气相与液相，VOF法可通过求解其中一相体积分数的连续方程，完成气液两相界面追踪。第q相流体体积方程为：

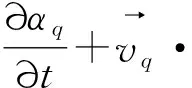
(3)

主相体积分数的计算基于以下约束：

(4)

1.2 液体固有频率的确定

横摇激励下，液舱内流体的固有频率为fn，矩形舱内晃荡液体的固有频率可以由Faltinsen[4]给出的n阶自振频率表达式进行估算：

(5)

ωn=2πfn，

(6)

式中：L为液舱长度，m；h为液面高度，m；g为重力加速度，m/s2；ωn为角频率速度，rad/s。

本文主要考虑n=0时，低阶模态下的舱内液体的固有频率，即共振频率。

2 模型建立与数值方法验证

采用Fluent软件建立三维矩形刚性舱，模型尺寸为100 0 mm(长)×400 mm(宽)×600 mm(高)，载液率为50%，监测点分别为A、B、C、D，具体参数如图1所示。

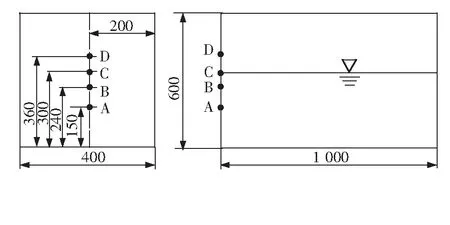
图1 矩形液舱计算模型示意图

2.1 初始条件设置

液舱舱壁材料选用刚性材料，液舱的四周壁面全部设为无滑移壁面，舱内流体采用原油，设定黏度为0.229 Pa·s，密度为950 kg/m3。液舱内部的气体压力设置为1个标准大气压，且忽略原油的蒸发对气体压力造成的影响。

考虑到晃荡过程是一个瞬态非定常过程，且要求算法精度较高，故采用基于压力求解的非耦合隐式算法中的PISO算法进行求解，对流项以二阶迎风格式差分进行离散，运用VOF模型来追踪自由液面变化，考虑到液体的黏性，采用RNG-k-ε湍流模型进行计算。

液舱的运动通过加载UDF来实现，液舱做正弦横摇运动，晃荡中心设置为液舱底部中心，晃荡开始时液舱向左侧运动。具体参数见表1。

表1 液舱运动模态及参数

2.2 数值方法验证

本文选用文献[5]中的模型试验，验证数值模拟的正确性。模型的尺寸为92 cm×46 cm×62 cm，监测点选取模型右侧面中垂线上的点，距底面17 cm。舱内的液体采用自来水，晃荡周期为4 s，振幅为4°，晃荡中心是液舱的体心。运用VOF模型与RNG-k-ε湍流模型，并结合动网格技术进行计算求解，选取液舱侧壁面监测点的压力作为特征参数，将计算结果与文献[5]的试验结果进行对比，由图2知，本文的数值方法结果与试验结果吻合较好，表明该数值方法的准确性。

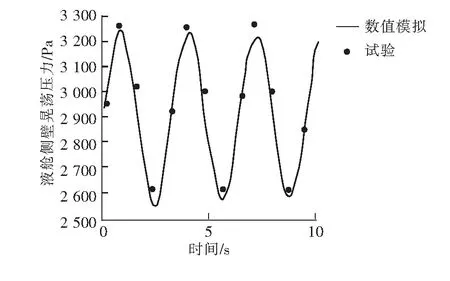
图2 液舱晃荡数值方法的验证

3 共振频率下油船液舱晃荡特征分析

3.1 左舱壁自由液面波高分析

根据上述模型，按表1工况进行模拟。共振频率晃荡情形下，左侧舱壁波高历时曲线如图3。

图3 左舱壁处自由液面波高历时曲线

由图3知，从第1个周期开始，波高逐步增加；第2个周期内，波高增幅最大；在第3个周期内，最大波高达0.3 m，这表明在第3个周期时，舱内液体发生冲顶现象；从第4个周期开始，波高始终保持最大值，呈周期性变化。分析上述现象的原因是：第1个周期时，由于液舱刚开始晃动，舱内液体从静止开始运动，液舱晃荡的幅度较小，液面爬升的高度较小；第2个周期时，液舱内的液体已经具有一定的速度，在动能和惯性力作用下，波高增幅快速增加；在第3个周期随着液体内部能量不断累积，发生了冲顶现象；由于外界激励不发生变化，因此从第3周期开始，波高呈周期性变化。

3.2 共振频率下油船舱内原油自由液面波动分析

随着晃荡的进行，舱内液体的波面在惯性力及重力的作用下也会呈现不同的状态。图4为液舱晃荡的波面变化图。从图4中可知，前2个周期内，舱内原油主要以驻波的方式在舱内运动；在第2个晃荡周期末，即t=2.60 s时刻，舱内原油在右侧到达液舱顶部后产生破碎波；从第3个周期开始，舱内原油以驻波与行进波的组合波的运动方式在舱内运动，并且分别在左侧舱壁与右侧舱壁发生冲顶现象，产生少量的破碎波，在原油回落的过程中产生破碎波。

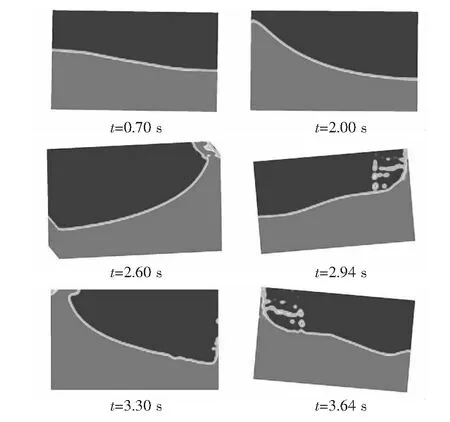
图4 不同时刻下的波面变化图

分析原因，在前2个周期，液舱的晃荡周期小，且液舱从静止开始运动，此时舱内原油以驻波的运动方式在舱内运动；在t=2.60 s时，液舱绕着底面中心轴向上运动，舱内原油的惯性力随着晃荡逐渐累加增大，使液体向上爬升，在右侧完成冲顶；第3个周期开始，舱内原油积累的动能越来越大，舱壁左侧的自由液面在惯性力的推动下，分别在液舱的左侧与右侧完成冲顶，到达顶部时产生少量的破碎波；舱内原油在下落过程中由于重力与外界激励作用向一个方向运动，原油在液舱舱壁阻挡作用下产生一个相反的运动速度，在2个相反速度的作用下，产生行进波，加上舱内原驻波的运动方式，产生组合波，同时舱内的原油也会产生破碎波。

3.3 共振条件下舱壁的晃荡压力分析

通过比较舱壁上不同监测点的晃荡压力(静压+动压)，得出舱壁的压力分布，主要分析A、B、C、D这4个点，具体A、B、C、D的晃荡压力历时曲线见图5。

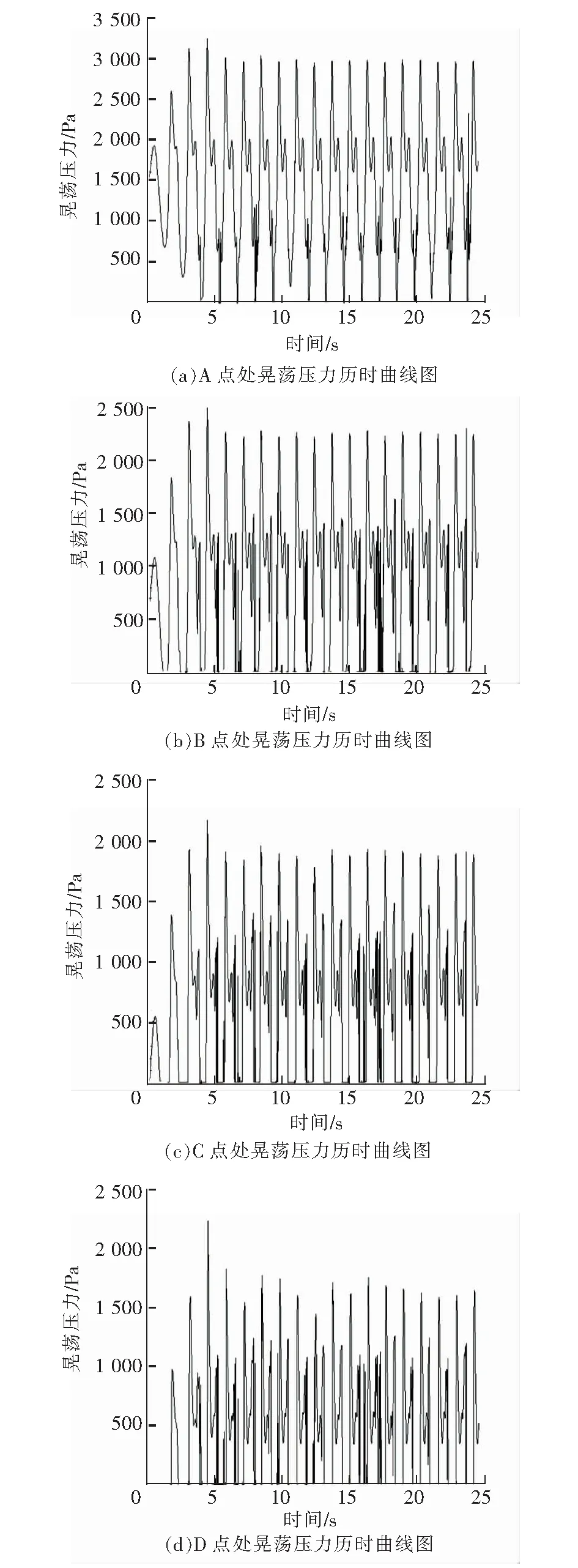
图5 不同监测点处晃荡压力历时曲线图

对比A、B、C 3点晃荡压力的峰值，在自由液面以下，距离自由液面越远的地方，其晃荡压力越大。原因是在晃荡过程中，距离自由液面越远，其晃荡程度较小，舱内原油的速度较小，动压也较小，此时静压处主导地位，故A点处晃荡压力最大，B点处晃荡压力次之，C点处晃荡压力最小；对比C、D 2点处的晃荡压力峰值，发现晃荡未达到稳定前，C、D 2点处的晃荡压力峰值基本保持一致，达到稳定状态后C点处的晃荡压力峰值要大于D点处晃荡压力峰值。这是由于原油接触舱壁时，其速度瞬间变为零，此时动压为零，而液体向上爬升到D点时，速度不为零，动压不为零，综合后C、D 2点处晃荡压力基本一致，待达到稳定状态后，此时静压处主导地位，C点的晃荡压力峰值大于D点的晃荡压力峰值。

4 结束语

1)当载液率为50%时，在共振频率下，左侧舱壁自由液面波高达到最大值的时刻是在第3个周期内，此时自由液面到达液舱顶部，第4个周期开始液面波高呈现规律性变化。

2)前2个周期内，舱内原油主要以驻波的运动方式在液舱内运动，从第3个周期开始，舱内原油的运动方式为驻波与行进波结合产生的组合波，并且原油在到达液舱顶部后回落时产生大量的破碎波，而冲顶时产生的破碎波较少。

3)在自由液面以下，舱壁受到的晃荡压力以静压为主导，距离自由液面越远，晃荡压力越大，自由液面以上，未达到稳定前，其晃荡压力峰值与自由液面处的晃荡压力峰值基本保持一致，稳定后静压处主导地位，距离自由液面越远，其晃荡压力越小。