基于有效降雨强度和逻辑回归的降雨型滑坡预测模型

盛逸凡，李远耀，徐 勇，吴吉明，林 巍

(1.中国地质大学(武汉)地质调查研究院，湖北 武汉 430074；2.中国地质调查局武汉地质调查中心， 湖北 武汉 430205)

滑坡是我国山地丘陵区主要的地质灾害类型之一[1]，突发性强、分布广泛，常常造成大量的人员伤亡和财产损失。大量调查研究发现，90%左右的滑坡发生在降雨期间或降雨之后，这种由降雨诱发的滑坡称为降雨型滑坡[2]。基于降雨事件与滑坡灾害间的关联性，通过区域降雨特征来开展大范围滑坡灾害的预测预报，是有效预防降雨型滑坡灾害的重要途径。

围绕降雨诱发滑坡的机理及预测预报方法，国内外学者开展了大量研究。如：Thomas Glade等[3]采用统计方法研究得出降雨诱发、非降雨诱发这两种情况下滑坡发生的降雨量阈值。F Guzzetti等[4]应用贝叶斯统计方法从大量数据中分析得出阈值曲线，发现山区的有效降雨强度要低于以地中海气候为特征的地区。国内方面，殷坤龙等[5]以浙江省为研究区，采用统计学方法分析了台风、非台风两种情况下滑坡与降雨强度、降雨量的相关性，得到了诱发滑坡发生的降雨阈值曲线及临界值。张珍等[6]、林孝松等[7]从降雨量、降雨周期、暴雨频次、雨型、以及降雨持续时间等方面进行了研究，指出了降雨与滑坡事件间的耦合。谢守益等[8]、李晓等[9]、谢剑明等[10]研究确定了区域性滑坡发生的临界降雨量值及降雨诱发滑坡发生的概率等，为地方气象部门滑坡预警提供了重要依据。

综合而言，针对降雨型滑坡的区域预测预报，最关键是确定诱发滑坡的临界降雨阈值。然而，在前人研究中，大多以统计方法和经验模型为主，对于降雨型滑坡本身的规模、形态等地形特征缺乏深入分析，常造成统计模型得出的宏观临界降雨阈值存在一定缺陷；此外，经验性的定性阈值模型与定量的预测模型也结合较少，从而造成统计阈值模型的适用性不足。

本文以湖南桑植县近30年的长时段历史滑坡灾害为研究对象，分析了降雨因子与滑坡事件概率及滑坡数量间的相关性和偏相关性；系统考虑滑坡地形条件对降雨阈值结果的重要影响，对降雨临界阈值统计结果按滑坡规模、滑体厚度、滑坡坡度进行分类，得出了不同类型滑坡的分类分级临界降雨阈值；并建立了基于逻辑回归方法的滑坡定量预测预报模型。

1 研究区自然环境与滑坡灾害

1.1 研究区概况

桑植县隶属湖南省张家界市，地处武陵山脉北麓，鄂西山地南端，全县总面积3 474 km2。区域属亚热带季风气候区，光热充足，春暖夏热多雨，秋凉冬冷雨少;年平均气温16.8 ℃.降雨量充沛，是湖南省的四大暴雨中心之一，多年降雨天数平均为140 d，多年平均降雨量1 417 mm，降雨量多集中于5—8月份，占全年降雨量的50%～60%。

区域地势总趋势为西北高、东南低，绝大部分地区地势高峻，群山起伏，沟谷深切，构造位于新华夏系一级构造第三隆起带的南段，湘西北弧形构造的东北端，属武陵山褶皱带的东南端，主体为桑植复向斜。境内地层除缺失白垩系、侏罗系、泥盆系下统及石炭系外，从第四系到寒武系地层其他均有出露，其中三叠系、志留系、寒武系分布范围较广，区内地质灾害主要发育在三叠系至志留系地层之中。

1.2 滑坡灾害发育特征

图1 1987—2015年月平均降雨量与滑坡数量统计Fig.1 Monthly average rainfall and the number of landslides from 1987 to 2015

根据湖南省地质调查院提供的桑植县地质灾害调查与区划报告得知，桑植县为地质灾害高发区，地质灾害类型包括滑坡、崩塌、泥石流和地面塌陷、地面沉降、地裂缝等，其中滑坡是最主要地质灾害，占灾害总数的94.1%。滑坡类型以浅层土质滑坡为主，规模为中小型，一般发生在暴雨期间。根据张家界市气象局和桑植县雨量站观测数据，结合中国地质调查局武汉地调中心提供的滑坡资料，统计分析了研究区内近30年的月平均降雨量与滑坡发生数量(图1)，可发现滑坡事件频数与降雨量的大小密切相关。现场调查表明，地形地貌、地层岩性等地质条件是控制区内滑坡形成和发展的内因，降雨是滑坡形成的主要外部条件之一。滑坡空间分布受地形地貌控制，分布于河溪两岸，发育于向斜、背斜及断裂附近，65%的滑坡的坡度分布在15°～30°之间。

2 滑坡灾害阈值判别模型

2.1 降雨量与滑坡的关系

在张家界市气象局和桑植县雨量站提供的近30年降雨数据和滑坡灾害资料的基础上，为了排除非降雨因素的影响，本文遴选出137例降雨诱发滑坡事件，表1列出了5例典型的降雨诱发滑坡事件和5例未发生滑坡的降雨事件。表中P0为当日降雨量，P1为滑坡前第1日降雨量，P2为滑坡前第2日降雨量，……，依此类推。由于桑植县降雨诱发滑坡的统计数据只精确到日，本文假设滑坡是在某日0-24时内发生，因此降雨量数据也取同时段内的数据。

表1 桑植县部分降雨诱发滑坡数据Table 1 Partial data of rainfall-induced landslides in Sangzhi district

表1表明前期降雨对滑坡发生起主要作用，由于前期降雨的持续作用，土体逐渐处于饱水状态，岩土体抗剪强度下降，即使在当日雨量很小的情况下，一旦有效降雨量高于临界阈值线，就可能诱发滑坡。所以，对于当日降雨量小或暴雨类型的滑坡，前期有效降雨量具有显著作用。

2.2 有效降雨量模型

有效降雨量是指对诱发滑坡发生作用的那部分降雨，这一概念最早是由Crozier在1980年引入地质灾害降雨阈值研究中的，近年来被广泛用于降雨诱发滑坡的研究中。降雨导致滑坡发生的过程可分两个阶段：第一阶段是前期降雨期，是指滑坡发生前一定时间内的降雨，降雨通常会使坡体土颗粒之间的空隙增大，随之孔隙水压力增加，有效应力降低，剪切强度降低，继而诱发滑坡灾害的发生[13-14]；第二阶段为持续降雨期，这部分降雨在一定程度上直接激发了滑坡的发生。由于每次降雨事件只有部分降雨量对滑坡的发生起作用，所以本文引入了有效降雨量，有效降雨量的计算公式为：

Pa=R0+KR1+K2R2+K3R3+…+KnRn

(1)

式中：Pa——有效降雨量；

K——降雨衰减系数；

R0——滑坡发生当日降雨量；

R1——次日降雨量，依此类推，n为滑坡发生前的天数。

自Crozier以来，计算前期有效降雨量时大多采用式(1)，通常需要根据相关地区灾害特点和地质条件的不同合理选取K值，或者对式(1)中降雨衰减系数的形式稍作改变。

桑植县由于山区面积较大，河流冲刷强，地下水动态变化复杂，雨季主要集中在5—8月份，特别是7月气温较高，降雨量充沛，蒸发作用明显，具有较为明显的地域特征，合理地选择前期降雨衰减系数可使滑坡预测更精确。因此本文用SPSS22.0软件做降雨因子与滑坡是否发生及滑坡数量的相关分析和偏相关分析[15-16]。

2.3 有效降雨衰减系数

在构建降雨型滑坡预测模型时，合理选取降雨因子是首要的问题。本文中的降雨因子考虑了当日降雨量R0、滑坡发生前第1日的降雨量R1、……、第6日的降雨量R6；为进一步分析滑坡是否发生及滑坡发生数量与降雨因子的相关关系，引入累积降雨因子和前期降雨因子两个概念[11]。其中，累积降雨因子是指滑坡发生当日及前一段时间内的降雨总量，前期降雨因子是指累积降雨量减去滑坡当日的降雨量。利用SPSS22.0软件分析了降雨因子与滑坡数量及滑坡是否发生间的相关性和偏相关性[1]，结果见表2、表3。

偏相关分析是指不考虑其它变量的影响下，对两个所关心的变量进行相关性分析，所得结果能够更好地反映真实情况。从表2可以看出，滑坡是否发生及滑坡发生数量与当日降雨量呈显著相关和显著偏相关(在0.01显著性水平下)，这说明诱发滑坡最为显著的因子是当日降雨量R0。由表2可知，从R0到R6，相关系数及偏相关系数呈现逐渐下降的趋势；从R4开始，降雨因子对滑坡发生的影响已变得很小，可忽略不计。同时发现，当日降雨量及前一天降雨量与滑坡发生数量之间呈显著偏相关，这说明大部分滑坡发生在暴雨当日或暴雨的后一天。

表2 降雨因子与滑坡相关性及偏相关性Table 2 Correlation and partial correlation between rainfall factors and landslides

注：** 表示在0.01显著性水平下，相关性及偏相关性显著。

表3 累积降雨因子与滑坡的相关性Table 3 Correlation between effective cumulative rainfall factors and landslides

注：** 表示在0.01显著性水平下，相关性显著。

由表3可知，滑坡是否发生与累积降雨因子呈显著相关，表现出先升后降的趋势，在累积4天达到最大值；前期5天降雨与滑坡发生数量及滑坡是否发生的相关系数很小，这说明前期降雨对诱发滑坡的作用有限，滑坡当日的降雨R0不能忽视。综上，选用累积4天降雨量(即滑坡前3日及当日降雨量)来建立滑坡的预测预报模型较为合理，即式(1)中的n确定为3。

式(1)中前期降雨衰减系数K的选择会对滑坡预报的准确性产生重要影响，因此前期降雨衰减系数的合理选择尤为关键。分别设置不同的前期有效降雨衰减系数K值(从1到0.5依次减小)，并计算出4 d有效累积降雨量，然后分别分析不同衰减系数下，滑坡发生数量及滑坡是否发生与累积4 d降雨量的相关性。从表4可以发现前期有效降雨衰系数K= 0.8时与滑坡是否发生及滑坡发生数量的相关性最高，综合分析统计结果，本地区前期有效降雨衰减系数K设置为0.8最为合适。

表4 不同衰减系数下累积4天降雨量与滑坡间的相关性Table 4 Correlation of 4 days cumulative rainfall and landslide under different attenuation coefficients

注：**表示在0.01显著性水平下，相关性显著。

2.4 计算降雨阈值的具体步骤

本文中降雨阈值指标为有效降雨强度(有效累计降雨量与降雨历时的比值)和降雨历时，计算降雨阈值的步骤如下：

(1)统计桑植县已有滑坡，结合滑坡灾害的规模、坡度和厚度，按体积将研究区滑坡分为大、中、小规模三类，按坡度将滑坡分为缓、中、陡坡度三类，按厚度将滑坡分为较小、中等、较大厚度三类。规模方面，将小于30 000 m3的滑坡定为小规模，30 000～100 000 m3之间的定为中规模，大于100 000 m3的定为大规模；坡度方面，将0～30°的滑坡定为缓坡度，30°～45°的定为中等坡度，45°～82°定为陡坡度；厚度方面，将0～3 m的滑坡定为厚度较小，3～5 m定为中等厚度，5～15 m定为厚度较大。

(2)以降雨持续时间的对数为横轴，以有效降雨强度的对数为纵轴，按规模、坡度、厚度分别统计滑坡有效降雨量(I)和降雨历时(D)的关系，得到不同规模、坡度、厚度下有效降雨强度和持续时间的滑坡事件的I-D图(图3～5)。

(3)根据I-D图，分别求取10%、50%、90%概率下诱发滑坡的有效降雨强度阈值线。其方程形式为I=aD-b，最后采用频数法进行降雨阈值的拟合。不同条件下诱发滑坡发生的有效降雨强度阈值方程见表5。

图2 滑坡规模划分曲线及小、中、大规模体积滑坡I-D图Fig.2 Intensity-duration(I-D) thresholds of landslides with large, medium and small volume

图3 滑坡坡度划分曲线及缓、中、陡坡度滑坡I-D图Fig.3 Intensity-duration (I-D) thresholds of landslides with moderate, medium and steep slopes

图4 滑坡厚度划分曲线及小中大厚度滑坡I-D图Fig.4 Intensity-duration (I-D) of landslides with large, medium and small thickness

(4)根据有效降雨强度阈值对滑坡灾害的危险性进行分级，可分为高、中、低3个等级[1，17]。当预警点落在90%阈值线的上方区域时，则说明有效降雨强度已经超过滑坡发生概率为90%时的临界值，此预警区为高危险区；当预警点落在50%阈值线的上方时，则说明有效降雨强度超过了滑坡发生概率为50%时的降雨强度，此预警区为中危险区；10%到50%之间的为低危险区；10%阈值线以下的区域即无危险区(表6)。

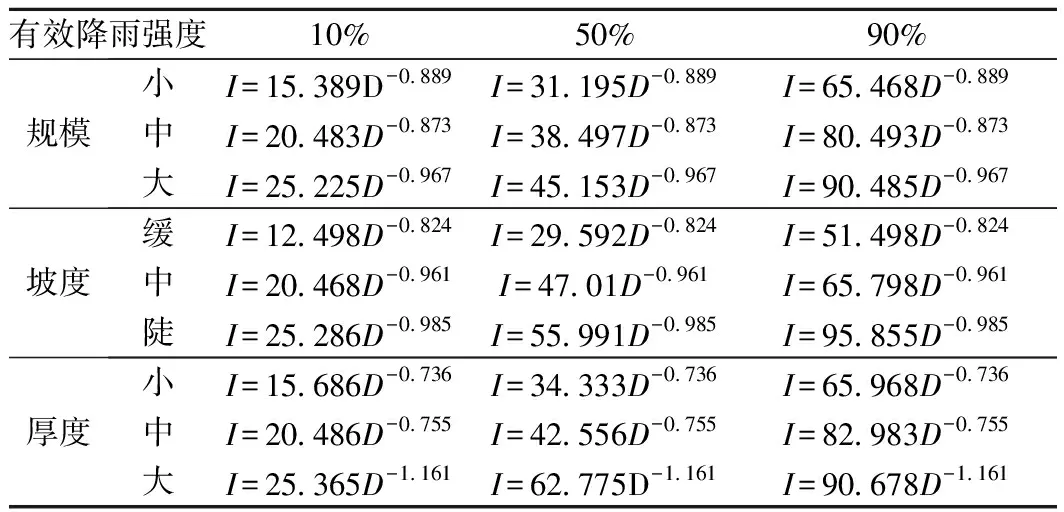
表5 不同规模、坡度和厚度滑坡的有效降雨强度阈值线Table 5 Effective rainfall intensity threshold line for landslides of different sizes, slopes and thicknesses

表6 滑坡危险性分级Table 6 Risk grades distribution for landslide

3 基于统计学方法的定量预测模型

3.1 基于逻辑回归的滑坡预测模型

逻辑回归是一种基于统计学和确定性模型相结合的分析方法[18]。考虑到降雨因子为非连续变量，本文使用逻辑回归分析中的二元逻辑回归方法[1]。

假设某研究区发生滑坡的概率为p，p的取值范围为0到1，则不发生滑坡的概率为1-p，p/(1-p)为滑坡逻辑回归值。对其取自然对数，自变量为X1，X2，…，Xk，其中X1为当日降雨，X2为前一天降雨，……，依次类推；因变量为滑坡发生概率p，则逻辑回归方程可表示为[20]：

(2)

式中：β1，β2，…，βk——回归系数。

变换式(2)可得：

(3)

利用式(3)可以定量预测降雨型滑坡灾害发生的概率。

3.2 滑坡预测模型的建立

将滑坡发生定义为逻辑值1，未发生定义为逻辑值0，把概率p= 0.5作为预测降雨型滑坡是否发生的临界值点，p大于0.5时被认为会发生滑坡，p小于0.5时则认为不会发生滑坡。

本文首先从桑植县137例样本中遴选出120例发生滑坡事件。根据前文的分析，发现选用累积4天(即滑坡当日及前3日)降雨量、有效降雨衰减系数k=0.8时，建立滑坡的预测预报模型最为合理的结论。这两个关键因子的确定为基于二元逻辑回归的滑坡定量预测模型的准确度提供了基本保证。

将当日降雨量(R0)和前3日有效累计降雨量(Ra3)作为自变量，将滑坡是否发生(0或1，即二元逻辑)作为因变量，根据选取的120组样本值建立回归方程，另选10组降雨事件作为检验样本。经回归分析，得到滑坡发生的概率预测模型[13]为：

(4)

为了验证式(4)的准确性和实用性，选取桑植县诱发滑坡的5次降雨事件及未发生滑坡的5次降雨事件进行验证。将降雨因子代入式(4)，结果见表7，概率预测值与实际情况较为吻合。以概率值0.5作为滑坡是否发生的分界值，结果表明本文建立的滑坡预测模型准确性与实际情况吻合，见表8。

表7 10组样本预测值Table 7 Predicted of 10 sets of samples

表8 模型预测分类表Table 8 Classification of model prediction

3.3 临界阈值的确定

通常所说的临界值是指当研究区的降雨量到达某一个值时滑坡会发生，它实际上就是一个界限阈值，具体指滑坡事件发生在量上所需要的一个最大值或者一个最小值。因此，本文定义降雨量临界值为最小降雨量值。当降雨量大于或等于这个界限值时，会发生滑坡。桑植县符合要求的降雨型滑坡事件共120例，因此选用这120个滑坡发生当日降雨量和前三日有效累积降雨量这两个评价因子，继而得到临界值[20]表达式为：

R0=-0.566Ra3+70.61

(5)

式(5)中R0为当日降雨量，Ra3为前三日有效累积降雨量。当Ra3= 0时，即无前期降雨量，诱发滑坡的日降雨量临界值为70.61 mm；当R0= 0时，即无当日降雨，诱发滑坡前期降雨值为124.75 mm。

4 结论

(1)以湖南省张家界市桑植县为研究区，分别分析了滑坡发生数量及滑坡是否发生与降雨因子的相关性和偏相关性，结果表明，距滑坡发生后天数的增加，降雨因子与滑坡的相关性呈现出下降的趋势；当前期有效降雨衰减系数K=0.8 时，4天有效累积降雨量(即滑坡当日及前3日降雨量)与滑坡是否发生的相关系数最高。

(2)按滑坡的规模、坡度和厚度大小统计了桑植县滑坡灾害点的有效降雨强度和降雨持续时间数据，分别给出了不同类型滑坡的I-D图，定性得到了不同概率下诱发滑坡发生的有效降雨强度经验阈值，并对滑坡灾害进行了危险性等级划分。

(3)从定量角度建立了基于当日降雨量和前三日有效累积降雨量为自变量的二元逻辑回归方法的滑坡预报模型，经验证表明其预测结果较为准确。在此基础上，给出了临界值的表达式，为桑植县滑坡预测预报提供了依据。