金属阻尼器参数与金属阻尼器减震效果相关性研究

侯逸冰 严 焱 张新钰

(江苏科技大学，江苏镇江 212000)

1 概述

消能减震设计是通过消能装置耗散或吸收地震能量，把结构物中的某些构件设计成消能构件或在结构物的某些部位装设阻尼器，立足于“耗能”。当外部遭遇风荷载或小震作用时，消能构件和阻尼器处于弹性状态，结构本身具有的抗侧移刚度足以满足正常的使用要求;遭遇强烈地震作用时，消能构件或阻尼器率先进入非弹性状态，从而保护主体结构在强震中免遭破坏耗地震能量，从而减小结构在地震中的相对动能或势能以及结构的变形能。消能减震技术克服了传统“硬碰硬”式的抗震设计方法，为建筑的抗震设计和抗震加固提供了一条崭新的途径，具有安全、适用、经济、技术合理等优越性。金属在进入塑性状态后具有良好的滞回特性，并在弹塑性滞回变形过程中能吸收大量能量，因此被用来制作不同类型的阻尼器。将金属阻尼器在结构不同的位置设置，将所得结果相互分析比较，从而得到金属阻尼器在高层钢框架结构中的最优布置位置;以等效线性化理论，能量平衡理论以及倍数法理论的消能减震结构设计方法为基础，分别计算结构附加阻尼器的阻尼量。研究大多和金属阻尼器的位置以及数量相关。本文进一步研究金属阻尼器内部因素:屈服强度、刚度、屈服位移以及三者对附加金属阻尼器消能减震体系的影响。

2 金属阻尼器参数与滞回曲线

金属阻尼器的滞回曲线概括了阻尼器的刚度、强度、屈服位移等力学特性，滞回曲线环所围成的面积可衡量阻尼器吸收能量的能力。图1用双线型模型来表示金属阻尼器的恢复力—位移滞回曲线。图2为滞回曲线骨架模型。

图1 金属阻尼器滞回曲线图

图2 金属阻尼器滞回曲线骨架模型

金属阻尼器的三个主要参数:刚度、屈服位移、屈服强度分别对应滞回曲线骨架模型中的第一刚度kd、第一屈服位移udy、屈服强度Fd。三者之间的关系符合式(1)。

为了研究第一刚度kd、第一屈服位移udy、屈服强度Fd对金属阻尼器减振效果的影响，将原结构附加的金属阻尼器，并分下列两种情况来讨论消能减震体系的地震反应:1)保持屈服位移udy不变，改变阻尼器抗侧刚度kd和屈服强度Fd;2)保持阻尼器抗侧刚度kd不变，改变屈服位移udy和屈服强度Fd。

3 计算模型

原结构采用单质点模型，并附加金属阻尼器组成消能减震体系，连接形式如图3所示。原结构抗侧刚度kf=1.18×108N/m，质量为:m=1.55×107kg，其自振周期为2.276 s。图3中kf为原结构抗侧刚度，c为原结构内部粘滞阻尼，kd为金属阻尼器的抗侧刚度。

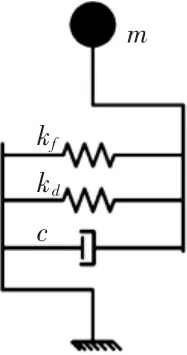
图3 单质点消能减震体系

4 振动微分方程和地震动

消能减震体系在地震作用下的振动微分方程为:

其中，［m］为结构质量;［c］为结构内部粘滞阻尼矩阵;kf为主结构的抗侧刚度;kd为附加的金属阻尼器抗侧刚度，在金属阻尼器屈服前后，kd的值也会发生着变化。{¨x}，{x}，{x}分别为结构加速度、速度、位移反应量;¨xg为地面地震动加速度。

本文采用两条地震波对结构进行弹塑性时程分析，使用wilson-θ法进行结构地震响应计算。由于改变阻尼器刚度后，整个结构的周期也会发生变化，而自然波的频谱特性对基本周期不同的结构产生的地震作用不同，所以采用人工波进行时程分析，称为建筑波，作用时间为60 s，时间间隔为0.01 s，其加速度时程曲线如图4所示。为了得出结构在罕遇地震和多遇地震作用下的情况，设定地震波加速度峰值为5 m/s2和0.7 m/s2。

5 设置金属阻尼器消能减震分析

5.1 保持屈服位移udy不变，改变阻尼器抗侧刚度kd和屈服强度Fd

设定金属阻尼器的抗侧刚度kd分别为原结构抗侧刚度的1倍，2倍，3倍，…，20倍，0倍情况即为原结构，金属阻尼器的屈服位移udy均为0.004 33 m。分别将附加不同金属阻尼器的结构命名为结构－1，结构－2，…，结构－20，结构－0为原结构。

对附加不同金属阻尼器的结构进行时程分析，得出结构在地震波的罕遇和多遇地震作用下的地震响应。分析结果如下:

图5，图6分别表示附加各个金属阻尼器的结构在地震作用下的最大位移反应值、最大速度反应值。随着阻尼器抗侧刚度kd和屈服强度Fd的增大，结构的最大位移值、最大速度反应值呈降低趋势。在罕遇地震作用下，结构的最大位移值、最大速度反应值下降趋势明显，而结构在多遇地震作用下，最大位移值、最大速度反应值下降逐渐变缓。

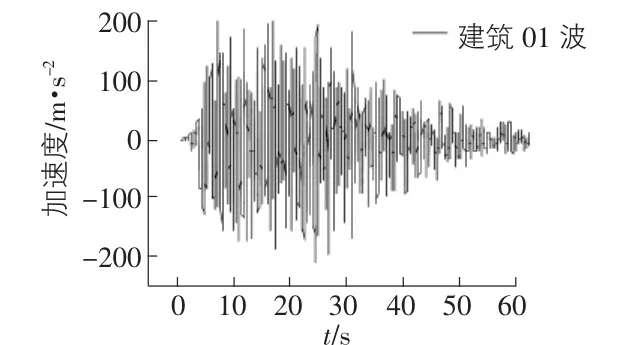
图4 地震波

图5 最大位移反应值降低率

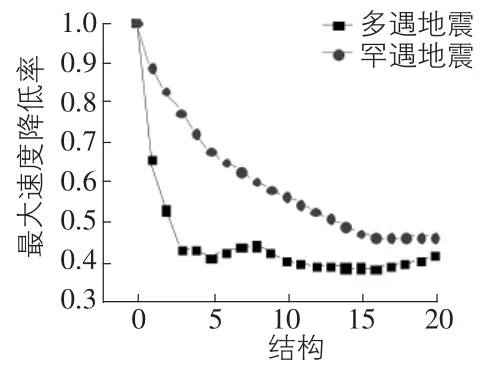
图6 最大速度反应值降低率

图7 表示各个结构在罕遇地震和多遇地震作用下的最大加速度反应值。结构在罕遇地震作用下，最大加速度反应值随着金属阻尼器抗侧刚度的增加有明显的降低趋势;而结构在多遇地震的作用下，最大加速度值随着金属阻尼器抗侧刚度kd和屈服强度Fd的逐渐增大，呈先降低后增大的趋势。

通过比较推断，增加金属阻尼器的抗侧刚度kd和屈服强度Fd，在罕遇地震作用下，金属阻尼器的减震效果逐渐增大;在多遇地震作用下，金属阻尼器的减震效果先增大，然后逐渐变小。体系经受多遇地震的地震波时，金属阻尼器抗侧刚度为原结构抗侧刚度的5倍为最佳效果。因为若继续增大倍数，结构地震反应值(位移值、速度值)减小不多，而体系的加速度值增大很多。

5.2 保持阻尼器抗侧刚度kd不变，改变屈服位移udy和屈服强度Fd

将原结构附加金属阻尼器，抗侧刚度kd=1.18×108N/m，初始屈服位移udy=0.004 33 mm。保持金属阻尼器的抗侧刚度，改变金属阻尼器的屈服位移，分别为原位移的1倍，2倍，3倍，…，20倍。分别将附加不同倍数金属阻尼器的结构命名为结构－1，结构－2，…，结构－20，结构－0为原结构。对附加不同金属阻尼器的结构进行时程分析，得出结构在地震波的常遇和罕遇地震作用下的地震响应。分析结果如下:图8～图10分别表示附加各个金属阻尼器的结构在地震作用下的最大位移反应值、最大速度反应值、最大加速度反应值。随着阻尼器屈服位移udy和屈服强度Fd的增大，体系在罕遇地震作用下，体系的最大位移值、最大速度反应值下降趋势明显，而后趋于平缓;体系的最大加速度值呈下降趋势。体系在多遇地震作用下，最大位移值、最大速度反应值、最大加速度反应值先下降，后上升，最后趋于某一定值。

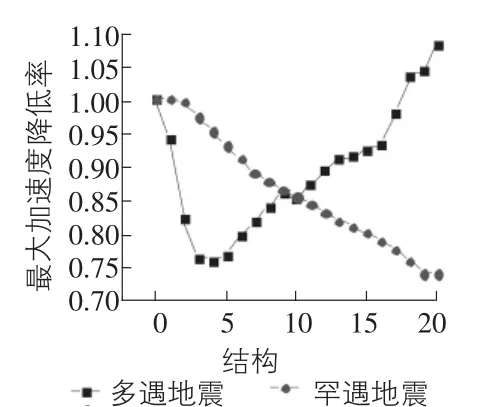
图7 最大加速度反应值降低率（一）

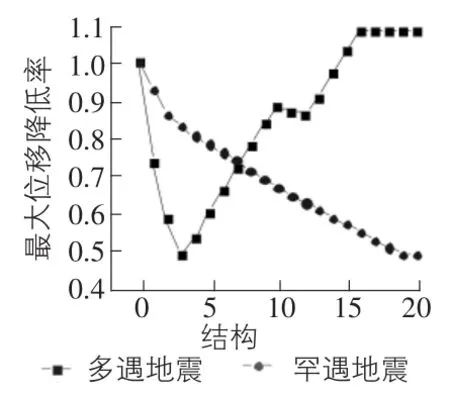
图8 最大位移反应值降低率

图9 最大速度反应值降低率

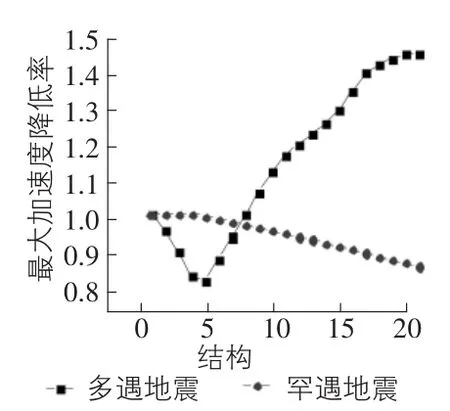
图10 最大加速度反应值降低率（二）

通过比较推断，金属阻尼器增加屈服位移udy和屈服强度Fd，在增幅不大时会使得金属阻尼器的减震效果变好，随着倍数的增加，金属阻尼器的减震效果逐渐变小，罕遇地震作用下的金属阻尼器减震效果趋于平缓;多遇地震作用下的金属阻尼器减震的能力逐渐消失。体系经受多遇地震的地震波时，金属阻尼器屈服位移为初始屈服位移的3倍为最佳效果。继续增大倍数，结构地震反应值:位移值、速度值、加速度值会呈增大趋势。

6 结语

通过对上述算例模型分析，得出如下结论:1)附加金属阻尼器的消能减震结构，随着金属阻尼器的抗侧刚度kd和屈服强度Fd的增大，金属阻尼器的减震效果变好，当结构经受多遇地震时，金属阻尼器抗侧刚度为原结构抗侧刚度的5倍为最佳效果。2)金属阻尼器随着金属阻尼器的屈服位移udy和屈服强度Fd的增大，金属阻尼器的减震效果呈现略微增大后持续变小的情况。当结构经受多遇地震时，金属阻尼器屈服位移为金属阻尼器初始位移的3倍为最佳效果。