不同埋深条件下直墙拱顶巷道破裂的数值试验

田志超，唐春安,2，刘业娇，李志兵

(1.东北大学资源与土木工程学院，辽宁 沈阳 110819；2.大连理工大学岩石破裂与失稳研究中心，辽宁 大连 116024；3.内蒙古科技大学矿业研究院，内蒙古 包头 014010；4.淮南矿业(集团)有限责任公司平安煤炭开采工程技术研究院有限责任公司，安徽 淮南 232001)

深部围岩巷道的破裂化现象能够反映深部岩体的非线性力学特性和工程响应的动态特征，在深部地下空间开发中起着相当重要的作用。鉴于此，国内外许多学者，如ADAMS等[1]、SHEMYAKIN等[2]、李术才等[3]、陈旭光等[4]、周小平等[5-6]、唐春安等[7]诸多国内外学者分别从理论推导、现场监测、模型试验、数值模拟等方面对巷道围岩破裂化现象进行了研究。特别是袁亮等[8]、王汉鹏等[9-10]在对深部巷道模型围岩分区破裂做了大量的物理试验研究，其中对于平面应变条件下，直墙拱顶巷道开洞荷载大小不同进行了对比试验研究，研究发现巷道围岩破裂具有一定的共性，例如开洞荷载较小的巷道(可视为浅部围岩巷道)，开洞后没有产生破坏，对于开洞荷载较大的巷道(视为深部巷道模型)，开洞时的破坏位置均是在左墙角和右墙角处产生平行于巷道轴线的裂缝。但同时随着荷载的增大发现最大荷载与开洞荷载比值越大，模型体表面破坏程度越轻。

然而，尽管对于深部岩体破裂化的研究取得了一定成果，但其研究仍处于初级阶段，还存在以下不足：浅部岩体的破坏准则并不能很好的应用于深部岩体，对于深部岩体破坏准则的研究和应用还不够深入；由于地质条件的复杂性，物理试验要完全模拟实际的地质条件，工作量巨大，耗费大量的人力和物力，而数值模拟软件能够发挥它的优越性。

因此，为了深入探讨不同埋深条件下直墙拱形巷道围岩破坏机理，本文在文献[8]～[10]物理试验结果的基础上利用RFPA2D软件对不同埋深巷道围岩进行数值模拟试验研究[11]，进一步丰富深部岩体破裂方面的有关研究成果，更好地指导深部地下空间的开发和应用工作。

1 数值试验模型体建立

为了比较不同埋深条件下巷道围岩受力变形的异同点，采用与实体相同的力学参数进行计算，模拟巷道围岩的破裂形态以及应力应变。

1.1 模型参数及边界荷载

岩石力学参数假定符合韦伯分布，岩石破裂采用摩尔-库仑强度准则判断[12]。相变准则控制参数见表1，模型体力学参数见表2。

表1 相变准则控制参数Table 1 Control parameters of phase transition criterion

表2 两种模型的力学参数Table 2 The mechanical parameters of the two models

1.2 计算模型网格划分及加载

为了减少建模时间和计算结果的差异性，将两种不同埋深巷道建立一种计算模型，只是在加载过程中改变加载力，体现巷道围岩的不同埋深。另外为了消除边界对巷道围岩破坏的影响，建立100 m×100 m的方形模型体，巷道拱高1.5 m，巷道跨度3 m，巷道尺寸见图1。

图1 模型巷道尺寸Fig.1 Model roadway size

为了提高计算精确度，将模型体划分为300×300个单元格，见图2。模型体加载为竖直方向和水平方向加载，模型计算边界加载条件见图3。

2 数值试验计算结果分析

2.1 巷道围岩破坏对比分析

2.1.1 巷道围岩最大剪应力破坏情况分析

通过图4能够发现不同埋深两种巷道围岩的破坏异同点。相同特点：一是在平面应变条件下，两种巷道围岩均发生了破坏，而且围绕巷道两帮和拱顶呈环状型破坏；二是随着荷载的增大，墙脚和拱顶部位剪切应力值超过极限剪切应力值，造成巷道会在拱脚、侧墙及墙角这一区域产生压剪型的滑移线状破坏。

图2 模型体网格划分Fig.2 Mesh of model body

图3 模型体边界加载条件Fig.3 Load condition of model body boundary

不同点是在平面应变条件下，尽管两种巷道围岩均发生了破坏，但M2模型的破坏区域要大于M1模型破坏区域；M2模型的拱顶和底板出现破坏，说明随着巷道埋深的增加，巷道围岩的破坏程度也增大。

2.1.2 巷道围岩主应力破坏情况分析

图5显示了两种不同埋深巷道围岩的主应力情况。两种巷道围岩的破坏均从巷道两帮开始，逐渐向拱顶和底部扩展。随着荷载的继续增加，在巷道围岩破坏的左右两侧均出现了最大主应力，即破坏可能性小的区域，但是破坏裂缝有从巷道的拱脚和墙角处继续向深部扩展的趋势，有绕过最大主应力区域的可能性，从而形成了一个环状区域，即巷道分区破裂现场形成。

2.1.3 巷道围岩声发射情况分析

图6为M1和M2模型的声发射情况，圆圈和点状的图案代表巷道围岩体受到拉应力作用。

结合图4和图5，在图6中能够发现巷道围岩的破坏均由拉应力造成。随着荷载的增加，M1模型声发射主要集中在巷道的拱脚、墙角和两帮，巷道的拱顶有零星声发射出现，说明M1模型围岩的破坏主要体现在巷道两帮和拱脚墙角处。M2模型除了M1模型描述的特征外，在拱顶上方和底部均出现了拉应力，而且巷道两帮、拱脚和墙角处的拉应力范围也比M1模型大。通过图6能够得出巷道围岩的破坏随着深部的增加巷道的拉应力范围也在扩大。

图4 两种模型巷道围岩最大剪应力破坏Fig.4 Maximum shear stress damage of surrounding rock in two kinds of model roadway

图5 两种模型巷道围岩主应力破坏Fig.5 Principal stress damage of surrounding rock in two kinds of model roadway

图6 两种模型巷道围岩声发射Fig.6 Acoustic emission from the surrounding rock of two model tunnels

2.2 巷道围岩应变数据分析

提取两种模型三个不同部位进行应变对比分析，即巷道的拱顶、侧墙和底板三个部位。所有应变受拉为正，受压为负。图7～9中的虚线为应变数据拟合曲线，r/D为测点距洞壁距离r与巷道宽度D的比值，εr为径向应变，εθ为环向应变，应变单位均为με。

2.2.1 巷道围岩拱顶径向和环向应变分析

从图7(a)可以看出M1模型和M2模型应变值在距拱顶r/D=0.4处交叉，M1模型应变曲线逐渐平缓，应变值趋于稳定，而M2模型应变值继续增大。另外M2模型拉应变区域要比M1模型拉应变区域大，即M1模型在距拱顶r/D=0.1范围内进入径向拉应变状态，拉应变值较小，M2模型在距拱顶r/D=0.2范围内进入拉应变状态。图7(b)显示了拱顶的环向应变情况，可以看出M1模型拱顶环向应变值小于M2模型对应应变值。M1模型在距洞壁环向应变没有出现进入塑性区的调整；M2模型在距洞壁r/D=0.6范围内应变出现进入塑性区的调整。

2.2.2 巷道围岩侧墙径向和环向应变分析

巷道围岩侧墙径向和环向应变对比分析见图8。

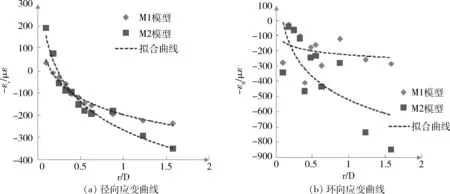
图7 巷道围岩拱顶应变数据对比Fig.7 Comparison of strain data on surrounding rock arches in roadway

图8 巷道围岩侧墙应变数据对比Fig.8 Comparison of strain data on surrounding rock sidewall in roadway

图8显示了巷道侧墙围岩径向应变基本处于拉应变状态，而围岩环向应变均为压应变。图8(a)显示了M2模型围岩径向应变要大于M1模型围岩的径向应变。随着距离巷道壁的距离增大，二者围岩由拉应变逐渐转为压应变，其中M2模型围岩拉应变区域(r/D<0.9)要大于M1模型围岩拉应变区域(r/D<0.6)，说明M2模型围岩破坏区域要大于M1模型围岩区域，结合图5和图6可得出此结论。另外巷道围岩进入压应变区域以后，二者的径向应变变化趋势近乎一致。图8(b)为环向应变拟合曲线，首先从图中可以看出M1模型侧墙环向压应变小于M2模型对应值。通过上述数据发现M2模型围岩应变值比较分散，浅部相对较为集中。M1模型在距侧墙洞壁r/D=1.0范围外，环向应变趋于稳定；而M2模型在至侧墙洞壁r/D=1.6处，环向应变也没有趋于稳定，这说明M2模型开挖造成的扰动范围较大。

2.2.3 巷道围岩底板径向和环向应变分析

巷道围岩底板径向和环向应变对比分析见图9。图9中显示巷道围岩无论是在浅部还是在深部绝大部分处于压应变状态。在图9(a)中M2模型有一部分径向应变为拉应变，这是由于M2模型荷载较大造成的，但是从图中也能够看到拉应变区域很小(r/D<0.15)，说明底板的破坏只集中在底部附近区域，结合图5和图6也能反映此问题。反观图9(b)环向应变值拟合曲线，M1模型底板围岩数据比较分散，而且在围岩体内部应变值较大。M2模型底板围岩拟合曲线呈直线分布，而且数据均匀分布在曲线周围，特别是在巷道底部附近区域(r/D<0.6)，数据高度集中，说明环向应变是巷道围岩底板发生破坏的主要原因。

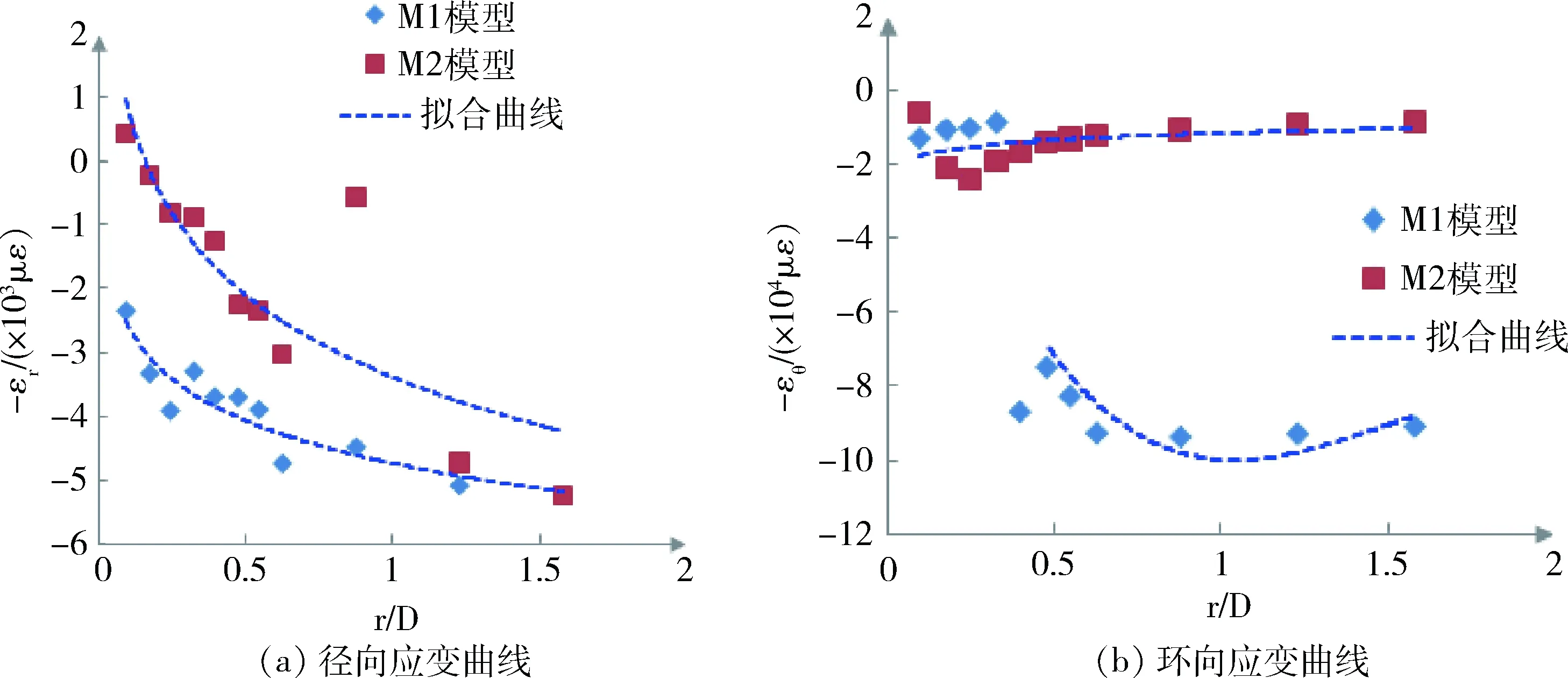
图9 巷道围岩底板应变数据对比Fig.9 Comparison of strain data on surrounding rock floor in roadway

3 结 论

1) 通过数值试验发现M1模型和M2模型巷道围岩的破坏初期规律基本相同，但是随着巷道埋深的增大，M2模型巷道围岩拱顶和底板也出现了不同程度的破坏。巷道围岩破坏均是从巷道围岩拱脚和墙角部位开始，由于这些部位随着荷载的增大，其剪切应力也变大，当荷载超过一定值后，围岩先从这些部位发生压剪型的滑移线状破坏。另外结合声发射模拟试验结果也能够发现巷道围岩的拱脚和墙角出现了拉应力。所以无论是M1模型还是M2模型，都应对巷道两帮和拱脚处进行加强支护。

2) 通过对巷道围岩的径向应变和环向应变数据进行拟合后发现，围岩内的径向应变是M1模型围岩和M2模型围岩破坏的主要原因。另外巷道围岩的环向应变值比较分散，规律性差，而且环向应变值均为压应变，所以将测得应变值拟合后发现环向应变对模型巷道的破坏影响微小。

3) 该数值试验结果与物理试验结果具有一致性，说明该软件可进行大量的数值试验研究，同时该研究方法丰富了深部岩体破裂方面的研究手段，可以更好地指导深部地下空间的开发和应用工作。