基于向量速度的超声血流量计算方法探讨

沈莹莹 杜宜纲 朱磊 冯赫林 深圳迈瑞生物医疗电子股份有限公司 （广东 深圳 518057）

内容提要： 文章探讨超声下基于向量速度的血流量计算方法，根据血管纵切面上的二维血流数据，分别采用最大流速近似法、流速均值近似法、矩形条近似法和环形近似法四种方法，计算六种不同模拟血流分布下，通过血管横截面的三维血流量，然后再与实际值进行对比。仿真显示采用环形近似法的计算结果最接近真实值。

目前常用的超声血流量测量方法有脉冲多普勒PW、彩色多普勒Color、能量多普勒Power和B-Flow测量等，其中PW血流量测量最为普遍。多个研究发现Color、B-Flow与MR测量结果较接近，PW比实际值偏大[1-5]。传统超声血流成像，如PW和Color，无法直接得到血流速度的实际大小和方向。PW测量需角度校正，一旦存在紊流则会产生测量误差。

动态向量血流成像V Flow是迈瑞Resona 7超声平台的一项全新血流成像技术[6,7]。它通过多角度偏转发射接收，得到实际血流速度在不同角度超声波束方向的投影，再依据三角函数关系合成实际流速大小和方向，并以向量速度的方式展现结果。该技术在用户端脱离了对超声波束扫描角度的校正依赖，比传统超声血流成像具有更高的时间分辨率，充分展示心动周期内各阶段血流波动的细节信息，尤其是在发生紊流的区域，具有传统彩超无法展示的临床价值[8,9]。

基于向量速度计算血流量，无需角度校正，且可以减少紊流带来的测量误差。然而，当前的V Flow是二维平面内的向量血流，测量的是三维空间中血流量，因此理论上仍然存在局限和误差。本文将探讨这种新的超声血流量测量方法，通过仿真对比不同计算方法、不同的三维血流分布下，根据二维血流数据计算得到的三维血流量结果的准确度。

1.基于向量速度的血流量计算模拟

探讨基于向量速度的血流量计算方法。图1为颈动脉横、纵截面示意图，血管壁分外、中、内膜，血管横截面直径D。理想状态下血流以层流分布，流速v呈抛物线分布，最大流速位于血管中心线。单位时间内的实际血流量Volreal为：

其中，为待测截面法线方向平均流速。实际中，血管可能有弯曲或斑块，导致血流为非层流，血流方向可能与管壁不平行，使PW测量方法产生较大误差。向量血流成像得到实际速度方向，也可得到垂直血管直径的流速或速度分量。相比传统方法，可大大减少非层流及角度校正导致的误差。

超声仪器中用户获得的二维向量血流速度分布，为血管横截面血管直径上的流速分布。除需将向量速度转换成沿直径垂直于横截面的速度分量（纯层流二者相等），还需注意不同估算方式在以超声二维图片推算三维流量的计算中对结果准确性的影响及对血流分布的鲁棒性。本文模拟4种血流量估算方法在6种不同速度分布下的计算结果。

以垂直经过横截面沿血管直径的最大流速一半作为红细胞流经此处的平均流速，与横截面面积相乘后得到当前帧血流量。假设血管直径上最大流速为vmax，则血流量为：

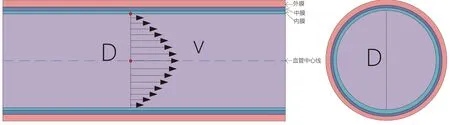
图1. 颈动脉横纵截面示意图

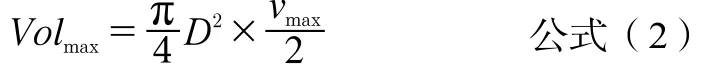
以垂直经过横截面沿血管直径的各点速度均值作为红细胞流经此处的平均速度，与面积相乘后得到当前帧血流量。假设垂直经过横截面沿直径有N点流速，各点流速为vi，则沿直径的平均速度为：

血流量为：

其中平均速度vd是沿直径各点的，而公式（1）v是整个横截面上的。

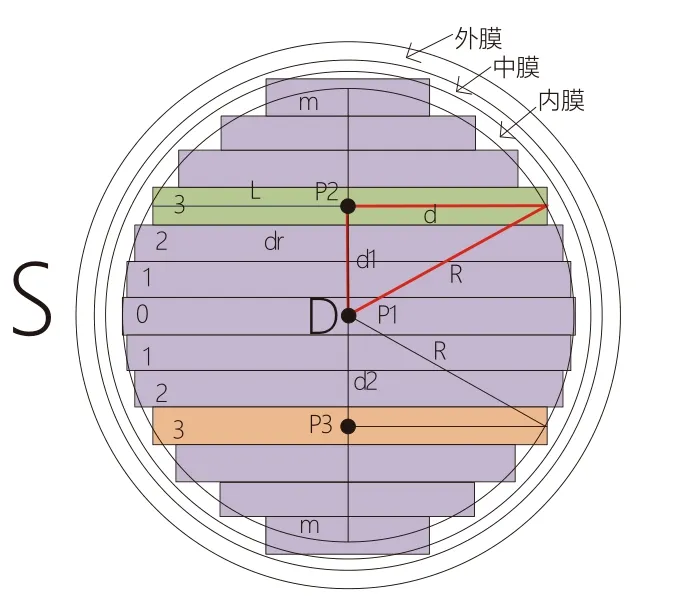
图2. 血管横截面的矩形条近似方法

图3. 血管横截面的圆环近似方法

将横截面近似成相同厚度的若干矩形条，各矩形内以垂直经过横截面沿直径的流速作为均值估计通过横截面的流量，如图2所示。

图2中，S为横截面，假设为规则圆形，圆心P1。超声声场所在的面在S平面上的投影与S相交为剖面直径D。在横截面上垂直于D得到厚度为dr的不同积分块，如图中所示。图2中以通过P2点的绿色矩形条为例，经过P2点与D垂直的直线与横截面相交得到线段L，其以P2为中心等分为长度为d的两段。P1与P2间距为d1。

向量血流成像可得P2处垂直于横截面的流速vi，以该值作为该矩形条内的流速均值。则该矩形条流量为假设d等分为2m+1个矩形条，d1、d2分别为上、下半圆矩形条与圆心距离，以圆心处矩形条编号为0，依次向上、向下分别编号为1、2、…m。则上下半区矩形条与圆心的距离可表示为：

半径与矩形条厚度的关系可表示为：

当前帧流量为：

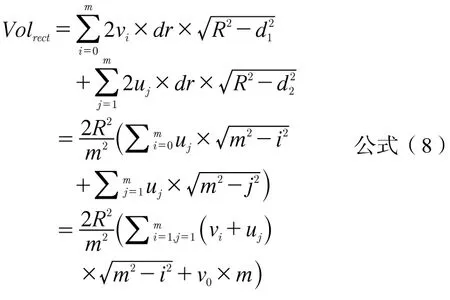
将横截面近似成多个相同厚度的圆环，各圆环在该直径上垂直于横截面的流速均值作为圆环内流速均值，以此估算横截面上的血流量，如图3所示。

图3中，S为横截面，假设为规则圆形，圆心P1，半径R，D=2R。向量血流超声声场所在的面在S平面上的投影与S相交为剖面直径D。将横截面S均分为n个圆环，各圆环宽度相等，为R/n。横截面上的流速取圆环在D上的交点均值，如图3所示的A和B，其流速分别为一段横截面上的流速viA和viB。流量为S面上n个圆环上的流量之和。使用公式（9）可得当前帧流量。

下面通过仿真验证上述计算方案的准确度。首先建立六种不同速度分布的横截面血流，如图4所示。其中，蓝线为血管直径，也是二维向量血流成像可探测位置。在模拟速度分布时，先选取一点给与速度最大值，再以该位置为中心，离它越远速度值越小。为进一步模拟实际情况，不同位置的速度值（包括最大值在内）再乘上一个正态分布的随机数。图4表示了六种不同最大值位置的速度不完全随机分布情况。其中，血管直径为6mm。左上为最大值居中；中上为最大值上偏0.5mm；右上为最大值上偏2mm；左下为最大值右偏2mm；中下为最大值上偏1mm右偏1mm；右下为最大值上偏1mm右偏2mm。图5展示了图4中对应的各子图沿直径的速度曲线。假设图4中各子图速度的最大值均为35cm/s。血管横截面内的实际血流量Volreal通过统计横截面上模拟的所有不完全随机分布的速度值结合横截面积计算得到。然后分别采用上述四种方法计算得到血流量Volmax、Volmean、Volmean、Volring。上述六种速度分布方式分别得到十组值，结果如图6所示。各组数据与真实值之间的误差分别求均值mean和标准差std，见表1。

表1. 六种血流量计算方式的误差平均值与标准差(mean±std)

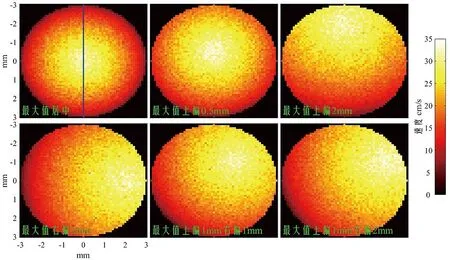
图4. 六种血管横截面速度分布图

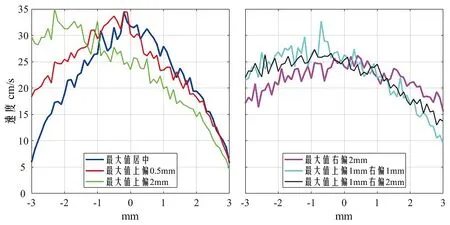
图5. 六种分布的血管直径处速度曲线

图6. 六种速度分布下，四种计算方法分别得到的十组血流量测值与对应实际值的比较结果

根据图6和表1的仿真结果可知，综合来看环形近似法结果Volring最为准确，且鲁棒性最高。均值近似法Volmean误差次之，但远不如环形近似法准确。最大流速近似法和矩形条近似法，其结果Volmax和Volrect不仅误差大且受速度分布影响大，计算效果不佳。但Volrect误差的标准差并不大，与Volmean和Volring都比较接近，且远低于Volmax。这说明矩形条近似法的测量稳定性比最大流速近似法好很多。此外，通过各矩形条的血流量，本文是根据中间位置的速度进行计算的，通常计算结果要高于实际值，如图6所示。因为一般情况下矩形条中间位置的速度最大，两边较低。但如果假设中间位置为最大值，按最大值的一半作为平均值进行计算，血流量结果又会偏小很多。因为整个横截面的最大值也可能是偏小的，而各矩形条的最大值也不一定都在矩形条的中间位置。再者，矩形条上的平均值与最大值的关系还与横截面速度分布情况有很大关系，也不能单纯的按照两倍比例进行计算。因此，矩形条近似法，还存在一定的提升空间，未来有待做进一步的深入研究。

2.讨论及总结

本文模拟了血管横截面上六种不同的速度分布，采用了四种血流量计算方法，其结果与实际仿真值做了相应对比。通过比较可知，采用环形近似法准确率最高，流速均值近似法准确率其次。最大流速近似法和矩形条近似法准确率均较低。但矩形条近似法的稳定性尚可，与流速均值近似法和环形近似法十分接近。基于二维向量速度的三维血流量计算实际上可以归纳为如何通过已知直径上的速度来准确预测整个横截面上的速度。未来如果能将几种方法结合起来，取长补短，血流量测量的准确性和稳定性还可以有进一步的提高。