利用OpenCL设计并优化FPGA上的全连接神经网络

周 鑫，安 虹，迟孟贤，金 旭，韩文廷

(中国科学技术大学 计算机科学与技术学院，合肥 230021)

1 引 言

随着人工智能的快速发展，现场可编程逻辑门阵列(FPGA, Field Programmable Gate Array，)凭借其强实时性和低功耗等优势获得广泛关注[1].利用 OpenCL 针对 FPGA 进行编程的开发方式因其开发简易的特点也获得了重视[2,3].

为探究利用 OpenCL 实现的全连接神经网络前向过程的效率与优化方法，本文利用 OpenCL 在 Intel Arria10 FPGA 上设计并实现了全连接神经网络前向过程，并针对系统的存储瓶颈，通过分组划分、数据复用、优化激活函数、单指令多数据流、浮点数半精化等策略进行了优化，平衡了系统中的资源占用情况，扩大了电路规模，提升了系统性能；优化后的版本与基准版本相比，得到了2.19x的加速.优化后，系统的 RAM 占用率达到94%，DSP 占用率达到42%.

2 相关工作

由于 FPGA 的强实时性非常适合神经网络的前向过程，很多开发者利用 OpenCL 针对卷积神经网络(Convolutional Neural Network)已经做了较为详尽的工作.Wang Dong 设计了流水线的卷积计算内核，并将工作开源[5]；Zhang Jia-liang 提出了衡量卷积性能的模型[6]，探讨了数据存储方式对性能的影响，并设计了 cache 、利用复用寄存器等技术进行了优化[6]；Naveen Suda 针对吞吐率，利用定点化技术进行了优化[7]；Utku Aydonat 利用 Winograd 算法实现了卷积运算，降低了访存需求，系统瓶颈不再是存储资源，而是计算资源[8].在卷积神经网络中，全连接层的计算量所占比重较小，因此，以上工作均直接复用卷积层的计算内核处理全连接层，并未深入探究全连接层的特点与优化方法[5-8].本文的工作针对全连接神经网络的特性，深入分析全连接网络的特点，提出了适用于全连接神经网络的系统设计方案，并针对基准系统中的瓶颈进行了一系列的优化.

3 OpenCL 模型

OpenCL 将计算分为主机(Host)端与设备(Device)端两个部分[10]，采用 offload 工作模式[9].设备运行 kernel 代码实现加速.Kernel 代码的一次实例化称为一个工作项(WI, Work Item)，多个执行同一任务的 WI 利用流水线实现并行执行；多个存在数据同步或互斥的 WI 组织为一个工作组(WG, Work Group); 多个存在数据依赖关系的 WG 合并为一个 N维工作空间(NDRange)[10].

每个工作项均拥有私有内存；同一工作组中，所有的工作项共享本地内存；一个工作空间内所有工作项共享全局内存.通常情况下，在 FPGA 中，私有内存由片上寄存器实现，因此访问速度最快，但容量有限；本地内存由 Block Memory 实现；全局内存由板载内存实现.

4 算法设计与优化

全连接神经网络的主要计算在全连接层和 Sigmoid 函数内.其中，全连接层的基本的数学计算公式为：

(1)

在全连接神经网络模型中，为了精确表示数据特征，每层的神经元的规模非常庞大.因此，优化思路应该集中在数据存储、减少计算量两方面.

4.1 分组设计

在全连接神经网络中，每层的计算量非常庞大.考虑将每层的神经元拆分为固定大小的计算组.根据这一思路，设每层节点数为S，将S个节点划分为K组，设C=⎣S/K」.将分组后的输入数据标记为Ci，i∈(1,…,K)；同时将每层每个节点对应的权值同样划分为K组，标记为Wij，i∈(1,…,K)，表示对应节点的编号；j∈(1,…,K)，表示权值组的编号.

下层神经网络的每一神经元的输入值由K组计算求得的部分和相加得出，其计算公式为：

(2)

由计算特性可知，各组之间无数据依赖关系.因此可以将相同编号的数据组与权重组的运算映射到一个 Work Item 上，实现粗粒度的组间并行计算.此时每个 Work Item计算局部的乘加和，每个Work Item 的结果相加即为下层网络中一个节点接受的值.

图1 数据与权值复用Fig.1 Reuse of weights and input feature

4.2 数据复用设计

4.2.1 数据复用设计

假设计算过程中，权值的路数为M，输入数据路数为N，权值与数据之间的计算关系如图1所示.

权值与输入数据的复用，可以实现一次取数，多次计算.因此，这一数据复用方式减少了数据的换出换入操作，降低了访存延时，提升了数据利用的效率，提高了全连接神经网络的并行处理能力.

4.2.2 存储设计

实现输入数据和权值的复用后，考虑结合多路输入数据与多路权值的排布特征，设计权值与输入数据的排布方式.

在初始状态时，同路数据按行优先的顺序存储在内存中连续的地址空间上，需多次访存读取多路数据与多路权值.因此，考虑采用列优先交叉存储的方式.顺序存储与交叉存储在访存时的区别如图2所示.

图2 顺序存储与交叉存储Fig.2 Sequential and interleaving storage

采用列优先的交叉存储模式可以大大减少访存次数.在同一 Work Group 中的Work Item 并行计算完毕后统一刷新，重新从内存中读取数据.这一策略可以减少访存次数，提高数据命中率，较好地发挥数据局部性优势.

4.3 SIMD 策略

划分计算组的策略将每一个计算组映射为一个 Work Item，Work Item 并行执行，实现计算组计算的并行.计算组内部则可以利用 SIMD 技术实现组内并行，提升数据处理速率.但 SIMD 的路数并非越多越好，因为 Work Item 的并行与 SIMD 并行都会占用大量的硬件资源，若多数据的路数超过了物理带宽的限制，反而对计算速度产生负面影响，应根据情况选择合适的 SIMD 路数.

4.4 Sigmoid 优化

Sigmoid 函数的公式为：

(3)

计算主要在e-x上.Sigmoid 函数具有对称性：函数关于 (0,0.5) 对称，因此可以只关注自变量在正数区间的计算，自变量为负数时，其函数值可以由自变量绝对值的 Sigmoid 函数得到[12]，如公式(4)所示.

(4)

同时，Sigmoid 函数具有饱和性.在x>12 后，函数处于饱和状态，函数值无限趋近于1，因此在x>12 后函数值近似为1[12].

实现Sigmoid函数的方法一般情况下有四种：利用泰勒级数计算、查表法、坐标旋转数字计算机法，以及分段函数逼近法[13].为寻找最优方法，通过实现泰勒级数法、查表法、分段函数逼近法分别进行实验.

4.4.1 泰勒级数法

利用泰勒展开式计算e-x，实现Sigmoid 函数.泰勒展开式为：

(5)

使用泰勒公式时，展开的级数对精度影响很大.在保证小数点后三位的精度时，至少需要进行5阶的泰勒级数展开来计算，浪费了计算资源，因此性能并非最优[14].

4.4.2 查表法

查表法利用采样的原理，将x对应的Sigmoid函数值储存在存储器中[13]，同时，利用对称性和饱和性减少存储规模.

但由于全连接神经网络对精度要求较高，采样点和其对应的Sigmoid函数值数目较多，因此需要较大的空间储存查找表，如设计采样间隔为10-3，为保证采样精度的准确性，使用16bit作为采样精度，需消耗192Kbit 的存储空间.

4.4.3 分段函数逼近法

由于Sigmoid 函数中e-x的计算比较复杂，因此考虑将Sigmoid 函数分段，每段使用简化的函数进行模拟计算，在计算Sigmoid 函数值时根据变量所在的区间，使用不同的简化函数计算公式进行模拟，得到Sigmoid的函数结果[15].同时利用Sigmoid函数的对称性和饱和性减少计算量.

根据Sigmoid 函数特征，以函数值的变化间隔对函数分段.为减少模拟函数衔接处的误差，将拟合误差较大的部分放入下一区间，同时适当缩小每个区间的跨度.经过实验得到9个分段函数，每段函数R2均为1，分段模拟函数的基本形式为：f(x)=ax3+bx2+cx+d分段区间内，模拟函数参数、结果与 Sigmoid 函数的最大误差如表1所示.

表1 分段模拟函数表Table 1 Table of section analogue function

此时，计算Sigmoid 函数时，利用自变量所在区间对应的参数使用三阶多项式函数模拟即可[16].将参数存储在 片上寄存器构成的 Cache 中，可以提高参数的访问速度.

利用9段模拟函数逼近时，误差波动范围较大，少数情况下误差可达10-3的数量级，如表1所示.由于全连接神经网络中每层神经元的数目十分庞大，因此，无法有效避免误差较大的数据出现；同时，由于全连接的结构，即使误差较小，经过全连接过程也会累积为较大的误差，对结果的精确性产生一定的影响.

因此，这一激活函数的模拟方法可以考虑使用在非全连接的神经网络结构中，降低计算的复杂度并保证精度，如卷积神经网络.

4.4.4 差分查表法

为了解决查表法对存储资源的浪费问题，尝试使用函数值分段与查表两种策略结合的方式实现 Sigmoid 函数设计，在保证精度的同时实现高效的 Sigmoid 计算.

如前所述，在设计 Sigmoid 的查找表时，可以利用函数的对称性和饱和性；储存对应表值时，采用0.5作为基准值，表中储存函数值相对于基准值的偏移量，可以减少用于表示函数值的数据的位数.

按照这一思路，设计差分查找表.

首先，在Sigmoid 函数自变量为[0,12]的区间内，按Δy的间隔对函数采样，得到共计0.5/(Δy)个采样点，作为构建查找表的基础.再将采样点分段标记，设第i段的第k个采样点对应的函数值与段首采样点基准值Basei的差值为Δi.k，则存储时只需储存各段段首基准采样点的函数值Basei和差值Δi.k.由于在节约存储空间的同时可以实现高效查找.如图3所示.

图3 差分设计Fig.3 Difference design

在储存Basei和Δi.k时，可以在不损失精度的前提下降低Basei和Δi.k占用的存储空间，压缩表的规模.例如使用16bit储存Basei的值，使用8bit 储存Δi.k的值，可以将查找表的规模缩小为原始表的四分之一.

4.5 半精设计

由于系统设计的主要瓶颈在于 RAM 的占用率与 DSP 的使用率非常不平衡，因此，需考虑降低 RAM 的占用率，提升 DSP 的使用率，来扩大电路规模和计算规模[17].利用半精化可以节省一半的存储空间，同时也可以保证一定的精度.输入数据和权重半精化的设计使存储的占用减少了一半，可以扩大电路规模和计算规模来进行优化，以提高吞吐率.

5 实验结果

5.1 神经网络模型

为衡量利用 OpenCL 实现和优化的全连接神经网络的性能，针对实际生产中使用的全连接神经网络模型设计实验，进行验证.这一网络由7层全连接层组成，其中每个单层网络均拥有2048个神经元，采用 Sigmoid 作为激活函数.

5.2 划分数据

由于数据组的个数与硬件资源消耗强相关，因此数据组的规模选择尤为重要.若数据组内数据规模偏大，则Work Item 的并行粒度较大，计算时间较长，同时对 RAM 的消耗较大；若数据组内数据规模偏小，则不利于组内进一步细粒度的优化.Intel OpenCL SDK 提供了优化分析报告帮助使用者查看系统资源的占用情况，如表2所示.由于系统中稀缺的资源为计算资源 DSP 与内存资源 RAM，全连接网络中很容易出现 DSP 与 RAM 消耗不平衡的情况，因此需要采用合适的取值进行计算组的划分.

表2 资源占用报告Table 2 Report of resource usage

表2是初始组内数据规模为32，即 C=32 时，系统资源占用比例.C 为32时，存储与计算资源的占用较为平衡，同时系统内仍有足够的资源支持下一步的优化.

5.3 数据复用

实现输入数据与权重的多路复用可以有效地提高数据命中率，如图4所示.

图4 数据复用率Fig.4 Reusing rate of data

根据访存带宽与计算带宽的限制，系统的采用16路输入数据和16路权值，即M=16，N=16.此时数据复用率由6.5%提升至99.7%.

5.4 Sigmoid 差分表

为保证数据精度，以函数值的变化设计采样区间.将y∈(0.5,1)的采样区间划分为5段，每段函数值的变化范围为0.1.段内按Δy=10-4的间隔对函数采样，得到5×103个采样点，使用16bit 储存表内数据时，查找表的尺寸为160kbit.利用压缩策略，使用16bit储存第i段的段首采样基准值Basei，8bit 储存偏移量Δi.k，其中6bit表示尾数，2bit表示指数，则查找表可以压缩为81kbit，节约了约一半的存储空间.

5.5 半精策略

半精策略，是将32 bit 的单精度浮点数转换为16 bit 的半精浮点数.这一策略以损失少许数字精度为代价，有效地降低了系统中的存储开销.采用半精策略后，RAM 占用率降低为初始值的一半，因此，可以将电路规模扩大为基准系统的两倍.

实现电路扩增后，系统的资源占用情况如表3所示.

通过表3可以看出，半精策略可以有效地降低存储开销，扩大电路规模.

表3 系统资源占用情况Table 3 Report of resource usage

5.6 对 比

将优化后的工作与基准工作进行对比，如图5所示.

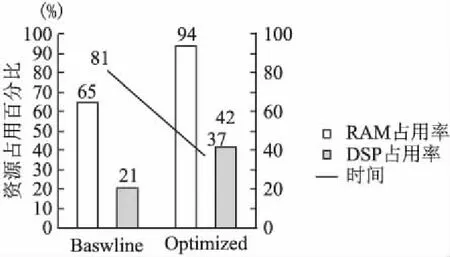
图5 优化前后的对比Fig.5 Comparison between baseline and present version

经过一系列的优化后，系统中的DSP使用率由21%升至42%，利用率提升了一倍；RAM 的占用，由65% 提升至 94%；单组数据的平均运行时间由81ms降低至37ms，得到了2.19倍的加速，如图5所示.此时限制系统进一步优化的瓶颈为 RAM 的容量.

6 总 结

本工作利用 Intel OpenCL SDK 在 FPGA 上设计并实现了全连接神经网络，同时针对 FPGA 的特点进行了进一步的优化.针对计算部分，在单路数据的基础上，实现了多数据的多路复用，讨论了在多种复用方式下分组策略的优化手段；针对激活函数，在传统解决方案的基础上，提出和实现了差分查表设计方案，在保证精度的同时节省了内存资源；针对 RAM 消耗过多的瓶颈，采用半精技术释放了有限的存储资源，有效地扩大了电路规模和计算规模.优化后，系统的 DSP 使用率上升了一倍，达到了 42%；系统主频达到了380MHz，并得到了2.19倍的加速.

利用 OpenCL SDK 实现的全连接神经网络充分挖掘了 FPGA 高能效比、低响应时延的优点，虽然在性能上有一定的损失，无法精确调配系统中的资源，但这一开发方式降低了 FPGA 的开发难度、缩短了开发周期、对软件开发者更加友好，性价比较高.