分层贪心聚簇算法研究

王炳乾，陈建华，许开行，卢健



分层贪心聚簇算法研究

王炳乾1，陈建华2，许开行2，卢健2

（1.成都理工大学 地球科学学院，四川 成都 610059；2.成都理工大学 地球物理学院，四川 成都 610059）

第三方地图API功能的增强给地图应用的搭建提供了便利，但是在地图应用中，经常会遇到海量空间点数据的显示问题。那么如何在有限的可视区域内利用最小的区域显示最全面的信息，同时又不产生影响地图可视化效果的重叠覆盖，就需要利用地图标记点聚簇技术。重点研究了采用KD-Tree的分层贪心聚簇算法，并基于OpenLayers API实现了该算法，对比分析该算法与基于距离的标记点聚簇算法在处理大量数据点时的运行效果。

海量空间点数据；聚簇算法；OpenLayers API；KD-Tree

1 引言

近年来，伴随着互联网科技的快速发展以及新兴技术的迅速崛起，浏览器端所能呈现的功能越来越丰富。应运而生的数字地图逐渐取代了传统地图的“地位”，独创性地将传统地图与网页相结合，并以其立体化、动态化、虚拟化的特点迅速成为新时代的宠儿，极大丰富和便利了人们的生活。

在用户体验上，数字地图为用户提供了一种信息与地图相结合的新的信息查询方式，而且信息的查询结果通常以标记点的形式直观、全面、精准地呈现在地图上[1]。但是，在数据急速膨胀的今天，海量的标记点数据如果同时呈现在地图上，不仅会大大增加客户端的渲染时间，造成客户端卡顿，更重要的是会使人产生密集恐惧症，极大降低用户体验的舒适度。为了解决这一问题，即在用户有限的可视区域范围内利用最小的可视区域展示最全面的信息，但又不产生数据的相互重叠，我们需要用到标记聚簇技术。由于不同的聚簇算法在显示效率上千差万别，效率的高低也直接影响着用户体验的舒适度，因此，考虑到聚合效率的问题，地图聚合通常采用原理简单、效率较高的聚合算法[2]，研究聚簇算法的效率也是文章讨论的重点之一。

聚簇分析是统计学的分支之一，学术界已进行了广泛研究，但以往的研究主要集中在基于距离的聚簇分析，诸如K-means算法、K-medoids算法及其他一些算法等，而且这些算法的聚簇分析工具早已被加入到许多统计分析软件包或系统中[3]。为了进一步提升聚簇算法的性能，弥补数据挖掘领域中聚簇方法的某些不足，学术界开始将聚簇方法与其他领域相结合，以期实现并发挥聚簇方法的最优性能[4]，常用的有免疫算法、蚂蚁算法、遗传算法等一些著名算法。就免疫算法而言，随着免疫计算的发展，人工免疫系统这一崭新的应用领域的出现，给聚簇分析领域注入了新的活力[5]。

目前，在线地图点聚簇算法已有较成熟的应用，很多在线地图API均提供点聚簇的功能。点聚簇算法不仅相对简单，而且很实用，但是如果缺少了，在线地图则无法对海量的标记点要素进行较好显示。因此，对于在线地图的二次开发者来说，这也是一个十分重要的功能，而且对于研究Web地图点聚簇算法有重要意义[6]。

2 分层贪心聚类

2.1 原理

2.1.1 分层贪心聚簇

将点集合到特定缩放级别中的简单有效的方法称为贪心聚簇（Greedy Clustering）[7]，它的工作原理如下：①从数据集的任何一点开始；②查找该点周围某一半径内的所有点；③与附近的点组成一个新的群集；④选择一个不属于集群的新点，并重复，直到访问了所有的点。

贪心聚类工作原理如图1所示。

图1 贪心聚类工作原理

对于地图的每个缩放级别，都进行上述步骤操作的代价是极其高昂的。例如，如果缩放级别是从0～18级，浏览器就不得不处理整个数据集19次，而且由于每个集群需要适应指数级增加的点数，所以在较低缩放级别上的聚类将变得很慢。通过重用计算可以避免这样的问题。对缩放级别18进行聚类后，将生成的聚类分组为新的z17聚类，使用z17簇形成16簇，以此类推，直至最小缩放级别。由于每个这样的步骤所需要处理的点数都呈指数下降，所以能快速对所有缩放级别进行聚类。分层贪心聚类工作原理如图2所示。

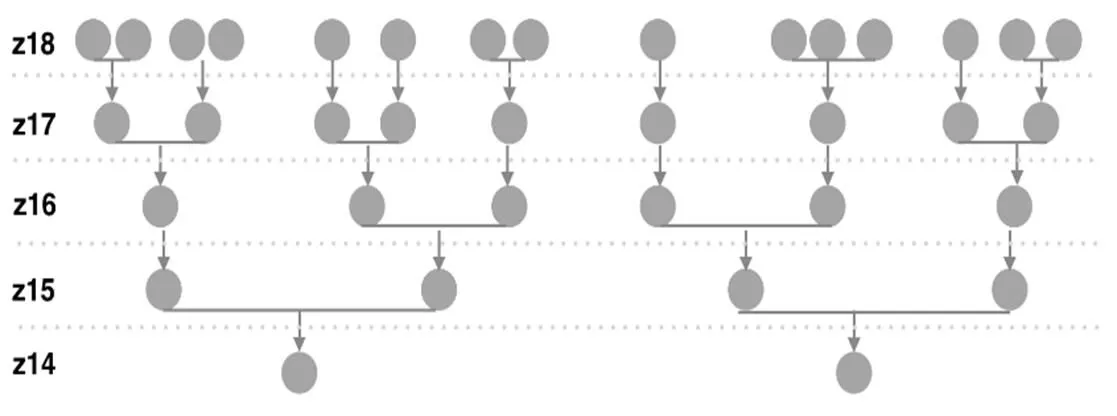
图2 分层贪心聚类工作原理

以上方法即为分层贪心聚簇（Hierarchical Greedy Clustering）[8]，不同于更复杂的集群算法，它可以迅速在浏览器中处理数百万个点，而且可以在交互式地图上浏览点数据集。在交互式地图中实现这种聚簇方法存在两个潜在的烦琐的操作：①找到一定半径内的所有点；②在当前屏幕上查找集群。

半径查询的最简单方法是循环遍历所有的点，并保存那些足够接近查询点的点。但是对于每个潜在的集群都需要进行多次这样的查询，难免造成效率低下的问题。另外，点击拖动或缩放地图时都需要这些点，如何遍历屏幕查询所有的点也是一个问题。为了有效解决这一问题，本文引入了空间索引，并利用空间索引中特殊的数据结构处理点，它的优势是能够有效、快速地进行查询，并立即进行任意数量的后续查询，KD-Tree数据结构即可完成这样的任务。

2.1.2 KD-Tree

KD-Tree是一棵二叉树，树中存储的数据是维数据。在一个维数据集合上构建一棵KD-Tree代表了对该维数据集合构成的维空间的一个划分，即树中的每个结点对应一个维的超矩形区域（Hyperrectangle）[9]。本文所用到的KD-Tree主要对二维数据集合所构成的二维平面进行划分。

KD-Tree作为BSP-Tree（Binary Space Partition Tree）分割空间时存在的特殊情况，在了解KD-Tree之前先对BSP-Tree进行简单介绍。BSP-Tree，即二叉空间分割树，也是一棵二叉树，基本思想是：任何一个平面都可以将空间划分为两个半空间，此外，如果在任何一个半空间中仍存在一个平面，这个平面将会继续分割该空间为更小的半空间。推广至二维平面，平面映射为一条直线，任何一条直线都能将一个二维平面分割为两个子平面。BSP-Tree分割二维平面如图3所示。接下来再不断划分，如此便构成了一棵BSP-Tree。分割线称之为分割超平面（splitting hyperplane）。超平面都垂直于轴的BSP-Tree就是KD-Tree，同样的数据集用KD-Tree来进行分割时，结果如图4所示。

KD-Tree算法可以分为两个部分，一部分是构建KD-Tree本身的数据结构，另一部分是建立在KD-Tree这种数据结构之上的查询算法。KD-Tree中每个节点表示了一个空间范围，每个节点中主要包含的数据结构如表1所示。

注：直线上的标记点为根节点，上面的点归为左子树，下面的点归为右子树

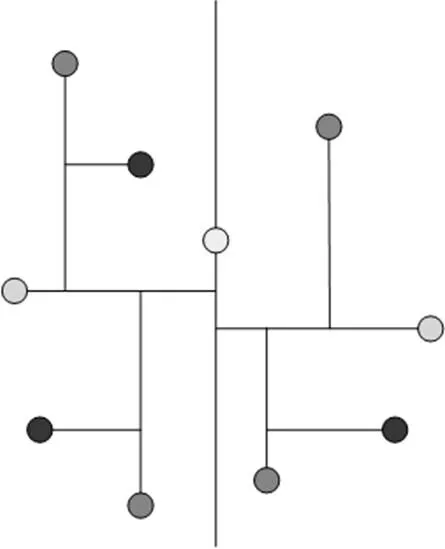
注：中间直线上的点为根节点，下一层是浅灰色，再下一层是深灰色，最后是黑色，这样就构成了一棵简单的KD-Tree

表1 KD-Tree中每个节点的数据结构

域名数据类型描述 Node-data数据矢量数据集中某个数据点，是n维矢量（这里也就是k维） Range空间矢量该节点所代表的空间范围 Split整数垂直于分割超平面的方向轴序号 LeftKD-Tree左子树 RightKD-Tree右子树 ParentKD-Tree父节点

轴点的选择是建立树的关键，当数据维度只有2维时，表1中Split的值可由、轴确定，可将两个轴分别编号为0和1，通过计算、方向上数据的方差，以得到的方差大小确定Split域首先该取何值，方向上的方差大则首先取0，反之则取1，即Split={0，1}或Split={1，0}，这里的方法称为最大方差法，方差越大，说明数据在或方向上的离散程度越大，即数据分布分散，此时在这个方向上容易将它们划分开，而且在该方向上进行的数据分割可以获得最大的平衡程度。建树需要遵循两个准则：①建立的树应尽量平衡，平衡度越高说明分割得越均匀，所用搜索时间也相应越少；②最大化邻域搜索的剪枝机会，所谓剪枝，可理解为在搜索算法中，通过某种判断避免一些不必要的遍历。

2.2 实验

SuperCluster（超级聚合）是由MapBox的工程师Vladimir Agafonkin于2016年发布的，是一个用于浏览器和节点的快速地理空间点集群JavaScript库。由于其对于Mapbox GL JS来说非常适用，所以将其作为一个独立的库发布，可以方便其他软件利用其进行快速算法。

实验中，同样基于OSM地图，本文在划定的矩形范围内进行了随机标记点的生成，初步设置了5 000个标记点。为了将分层贪心聚类算法与OpenLayers在线地图平台相结合，构建了名为superCluster的类，类中主要对OpenLayers地图上聚类结果的显示样式进行设置，使用时只需实例化此类，然后传入点图层数据即可。聚合前标记点分布情况如图5所示，聚合后分布情况如图6所示。

图5 点聚合前标记点分布情况

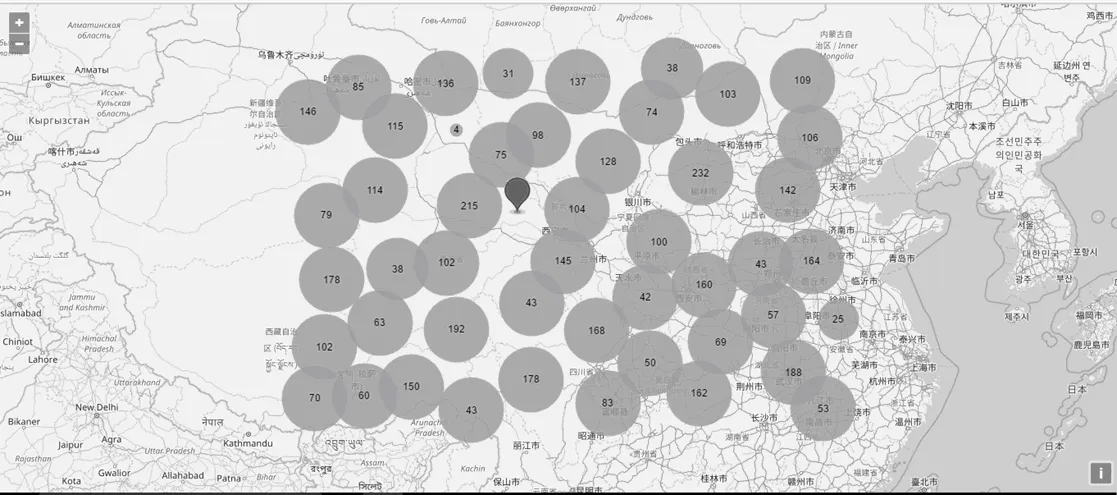
图6 点聚合后标记点分布情况

3 算法效果对比分析

3.1 算法运行测试环境概述

算法运行测试环境如表2所示。

表2 算法测试环境

操作系统Windows 10 CPUAMD A6-5200 APU with Radeon（TM）HD Graphics 2.00 GHz 系统内存4.00 GB 浏览器及其版本Google Chrome 58.0.3029.110

3.2 算法对比分析

实验中分别对20组数据点集合的算法运行效果进行测试，数据点数量为5 000～100 000，每组之间数据点跨度为5 000个点。取前7组效果对比，结果如表3所示。

表3中流畅、卡顿现象为运行算法进行不同缩放级别点浏览时地图显示点的情况。从表3可以看出分贪心聚簇算法较之基于距离的点聚簇算法在效果上有明显优势。后续实验中对分层贪心聚类算法进行了数十万乃至百万数据点的聚合，效果也十分明显，浏览不同缩放级别下点的情况也没有卡顿现象。基于距离的点聚簇算法由于迭代的原因，每个点集群均需对所有点进行遍历，运行效率可想而知。分层贪心聚簇算法本身即对分层数据进行处理，加之空间索引技术KD-Tree的使用对算法本身产生如虎添翼的效果。

表3 效果对比

数据点数量基于距离点聚簇算法运行效果分层贪心聚簇算法运行效果 5 000流畅流畅 10 000流畅流畅 15 000出现卡顿流畅 25 000卡顿流畅 30 000明显卡顿流畅 35 000明显卡顿流畅 40 000明显卡顿流畅

4 结论

通过比较分析，本文得出如下结论：基于距离的标记点聚簇算法虽然实现简单，但该算法对于海量数据点的聚簇实现效果不佳；分层贪心聚簇算法实现相对复杂，在加入了空间索引技术KD-Tree之后，该算法在处理海量数据点呈现聚簇效果上更具优势，且更适用于在浏览器上处理空间点聚簇显示，是一个非常优秀的算法。

［1］戴凤娇，肖林华，杨琭，等.基于百度地图的标记点聚合算法研究［J］.中国科技信息，2013（23）：82-85.

［2］刘果.基于网格密度的海量空间点聚合显示算法［J］.测绘与空间地理信息，2015，38（4）：174-176.

［3］黄韬，刘胜辉，谭艳娜.基于k-means聚类算法的研究［J］.计算机技术与发展，2011（7）：54-57，62.

［4］李波.基于单亲遗传算法的聚类分析研究［D］.呼和浩特：内蒙古大学，2011.

［5］方方，王子英.K-means 聚类分析在人体体型分类中的应用［J］.东华大学学报（自然科学版），2014， 40（5）：593-598.

［6］崔邓.基于智能手机轨迹提取停留点的时空聚类算法研究［D］.重庆：西南大学，2016.

［7］Gou S P，Zhang J，Jiao L C.SAR image segmentation based on Immune Greedy Spectral Clustering［C］//Asian-pacific Conference on Synthetic Aperture，2009：672-675.

［8］Ernst Althaus，Andreas Hildebrandt，Anna Katharina Hildebrandt.A Greedy Algorithm for Hierarchical Complete Linkage Clustering［M］.Berlin：Springer International Publishing，2014.

［9］杜振鹏，李德华.基于KD-Tree搜索和SURF特征的图像匹配算法研究［J］.计算机与数字工程，2012（02）：96-98，126.

［10］徐建民，李欢，刘博宁.在游戏中利用邻域特性扩展的KD-Tree及其查找算法［J］.计算机科学，2011，38（3）：257-262.

2095－6835（2019）01－0043－03

TP301.6

A

10.15913/j.cnki.kjycx.2019.01.043

〔编辑：严丽琴〕