考虑服务水平与动态转移规律的共享单车投放策略研究
鄢章华, 刘 蕾
(1.哈尔滨商业大学管理学院,黑龙江 哈尔滨 150028;2.泰州学院计算机科学与技术学院,江苏 泰州 225300)
1 引言
共享单车,学名互联网租赁自行车,是指企业在校园、地铁站点、公交站点、居民区、商业区等公共服务区所提供的自行车单车共享服务,其本质上是单车的分时租赁服务。由于共享单车符合低碳出行理念,政府对这一新鲜事物持善意观察的态度;定位技术、移动支付技术以及便捷的送还车技术(开、锁技术),在客观上为共享单车的迅速推广奠定了基础和条件;再加上共享单车并未像滴滴出行和Airbnb等共享经济模式那样深刻地影响既得利益群体的“蛋糕”,在行业推广的过程中阻力不大。受多方面利好因素的共同作用,共享单车行业的“摆车圈地”的速度十分迅速。根据交通运输部发布的不完全统计数据,截至2017年9月,全国共有共享单车运营企业近70家,累计投放车辆超过1600万辆,注册人数超过1.3亿,累计服务超过15亿人次[1]。共享单车所缔造的“自行车王国”是对世界环境保护奉献的中国智慧,更被誉为现代中国的“新四大发明”之一。但共享单车的疯狂生长也给城市管理带来了诸多问题,包括北京、上海、广州、深圳等一线城市在内的12个城市甚至先后宣布暂停新增共享单车新车投放[2]。在迅速成长的过程中,共享单车行业也暴露出诸多问题。一方面,城市里已经存在大量冗余的共享单车,另一方面,在通过APP和微信小程序端请求单车使用时,还有很多用户的用车需求得不到满足。在经历了“上半场”的疯狂扩张后,共享单车平台的科学化、精细化投放与运营,已经成为发展的主要方向。为此,2017年8月2日,经国务院同意,交通运输部、发改委等10部门联合出台了《关于鼓励和规范互联网租赁自行车发展的指导意见》,明确提出要根据城市特点、公众出行需求和互联网租赁自行车发展定位,综合考虑城市空间承载能力、停放设施资源、公众出行需求等因素,设计适当的车辆投放机制,这也是一步保障共享单车科学运营与调度的基础。就目前的形势而言,共享单车的科学投放与运营,已经不仅仅是企业层面亟需解决的问题,更是整个社会面临的管理难题。本文根据单车出行用户的基本需求,结合企业对服务水平的设计要求,分析各单车投放点的投放需求;在此基础上,基于马尔可夫过程描述单车分布随时空的变化情况,并结合需求约束构建单车投放的优化决策模型。该模型可以根据现实情况的需要调整时、空粒度,具有较好的通用性。模型的理论研究成果和案例分析结果,对于指导实践中单车投放和解决已存在的过度投放问题,具有重要的参考价值。
从总体上看,现有关于共享单车的研究大致可以分为如下的三个方向,这三个方向的内容也存在不同程度的交叉,为表述清晰,主要从如下三个方面进行梳理。
(1)选址优化。在选址优化的过程中,需要考虑很多方面的因素,不同的学者考虑的侧重点也各不相同。如Lin和Yang从满足特定服务水平约束的角度,优化单车投放站点的数量及站点间的网络结构[3-4]。Dell'Olio和Ibeas等根据潜在需求情况进行投放点的选址优化[5],García-Palomares等[6]基于GIS分析出行需求的空间分布与投放点容量限制,Frade和Ribeiro[7]考虑预算的约束,从最大化覆盖率的角度进行投放点的选址以及投放数量的决策。Nair和Miller-Hooks[8]从最大化利用率的角度优化单车在各投放站点配置,通过构建二层混合整数规划模型对问题进行建模求解。Askari和Bashir[9]在成本的基础上,增加安全的考虑,构建了相应的多目标优化问题,将多目标问题转化为单目标并通过遗传算法进行求解。 除利用解析模式来分析共享单车系统的设计外,仿真模型也是系统设计的重要手段,如Romero等[10]将仿真与优化模型结合起来,在分析交通模式与主体互动关系的基础上,构建仿真模型对停靠站的选址进行优化。总体而言,对于共享单车投放点的选址问题,影响因素和解决思路因具体问题的不同而各不相同,解析模型和仿真模型的使用也各有所长。本文在因素层面参考了服务水平的限制,在方法上则是将解析与数值仿真二者进行了结合。
(2)需求分析与预测。需求分析与预测的目的是通过对现有需求模式的分析,预测未来的需求情况,并以此为基础进行决策。总的来说,需求分析与预测方面的研究,大致可分为两个方面。其一是研究影响因素,即哪些因素会影响需求,一般包括时间、天气、人口、环境、土地等[11],有学者还发现路口和站点的空间分布也会影响需求[12];其二是分析与预测的方法,即怎样使用数据进行需求分析和预测,常用的处理方法包括网络的聚类加权[13]、动态网络规划[14]等。针对具体的问题,影响因素和分析与预测的方法又必须综合考虑。
(3)调度与平衡(Rebalancing / Redistribution / Repositioning)。共享单车系统要想充分发挥效果,不仅需要在适当的地方投放适当数量的车辆而且还需要周期性的重新分配(Redistribution),才能保障车辆的有效流转与使用[15]。如何通过调度与平衡避免由于供过于求(Congestion)和供不应求(Starvation)所导致的用户流失,已经成为共享单车企业在运营管理中的主要任务[16]。关于车辆调度与平衡的策略,可以通过用户激励的方式或弹性价格机制来改变用户的行为来实现[17],也可以通过卡车运输的方式[18],通过卡车运输调度也是现实中被大多数公司采用的调度方式[19]。单车调度与平衡的研究都是在既定的资源条件和策略下,通过对价格、调度量、调度线路等日常业务的具体内容进行优化,能在一定程度上缓解供过于求和供大于求的问题,但很难从根本上解决这些问题。
与本文关系紧密的前人成果主要是Lin Jenn Rong等[3-4]和Schuijbroek等[19]。其中,Lin Jenn Rong等[3-4]将服务水平引入到单车共享系统的设计中,从投放点的覆盖范围(距投放点一定的时间和空间范围内的需求总数为指标)和单车的可获得性(以用车需求被满足的比率为指标)两个方面来衡量单车共享系统的服务水平,对后续研究共享单车的投放与运营具有较好的启示作用[3, 4],这也为本文中服务水平的衡量提供了基本的方向,由于本文的模型可以通过空间的细分,从另一个角度反映出投放点的覆盖范围问题,在文中也就未明确体现出覆盖范围这一概念。与以往研究不同之处在于,本文更突出共享单车系统中需求的随机性,通过随机变量间的关系来描述服务水平,而不仅仅是用车需求的满足率。Schuijbroek等[19]将每个投放点看作一个有限容量的排队系统,认为投放点满足特定的服务水平时,单车的投放量会有上限和下限,而初始投放量满足服务水平的投放点被定义为自给自足型投放点(self-sufficient),这样的投放点是不需要额外调度的。的确,这样的投放点是不需要调入车辆的,但在该投放点用车需求较少时,该投放点还可以作为车辆调出点,通过“共享”实现投放量的节约。本文在分析单个投放点的车辆需求量时,借鉴了此文的做法,在排队系统的基础上,综合考虑使车辆库存数减少的用车需求和使车辆库存数增加的还车需求,在两方面因素的共同作用下,对满足特定服务水平的车辆需求量进行估计。
就目前的研究成果而言,定性的文献侧重于发展趋势、问题和对策等中观和宏观层面;定量的文献大多集中于车辆投放后的调度与管理问题,对共享单车的投放问题却很少涉及。由于好的运营管理会在一定程度上缓解投放不合理带来的问题,而差的运营管理则会进一步放大投放量不合理所带来的问题。考虑到共享单车系统出现的过程,科学地设计投放量才是共享单车系统良好运营的基础。针对目前中国共享单车行业的现状,仅进行调度的优化已无法彻底解决共享单车系统所带来的多种社会问题,必须开展市场、政府与社会协同治理[20]。因此,本文试图从单车投放量优化这一源头开始,正本清源地解决共享单车系统存在的问题。
2 问题分析与描述
2.1 问题范围界定与系统分析
本文考虑的关键问题有三个,其一是根据用户在各投放点的用车需求确定该投放点的投放需求;其二是对各投放点间车辆的动态流转网络进行描述;其三是综合考虑各投放点在不同时间段的投放需求与动态流转网络,优化总的投放量与投放策略。为突出关键问题,本文将重点考虑共享单车的总投放数量与投放数量在空间上的分布,对投放后单车的运营与调度细节暂不深入考虑(对单车运营与调度感兴趣的读者可以参看文献[19,21-23]等)。为此,本文对研究问题作如下假设:
(1)不考虑单车的丢失与损坏,单车一旦投入使用,就在系统中一直存续;
(2)在分析出行需求时,假定每一天利用单车出行的规律相同,对引发需求异常的情况,如节假日、庆典活动等暂不考虑;
(3)暂不考虑共享单车节点的容量限制,即节点可以满足共享单车的停放需求(我国的共享单车系统以无桩共享单车系统为主,节点容量可近似为无穷大)。
本文基于时空细分的框架,通过各投放点间单车数量的变化来从总体上描述共享单车系统的投放与运营情况,如图1所示。在时间截面i和i+1,共J个投放点的车辆保有量分别为:qi,j,j∈{1,2…J}和qi+1,j,j∈{1,2…J}。从i到i+1,各投放点间会有大量的车辆流入和流出,记该变化过程所对应的转化矩阵为Ri(状态转移矩阵),这个变化过程如图1中虚线部分所示。

图1 基于时空细分的单车数量变化情况
2.2 车辆需求量的分析与描述
考虑到共享单车系统中车辆的流动性,对于任意一个节点,在给定的时间段内,有车辆的流入和流出,节点j对单车的需求量记为dj(为达到一定的服务水平,企业为该节点配给的单车量),由于服务水平既可以从时间上[24]、也可以从数量上进行衡量[25],本文考虑需求量是从数量上进行衡量的。下面我们阐述如何进行dj的确定。
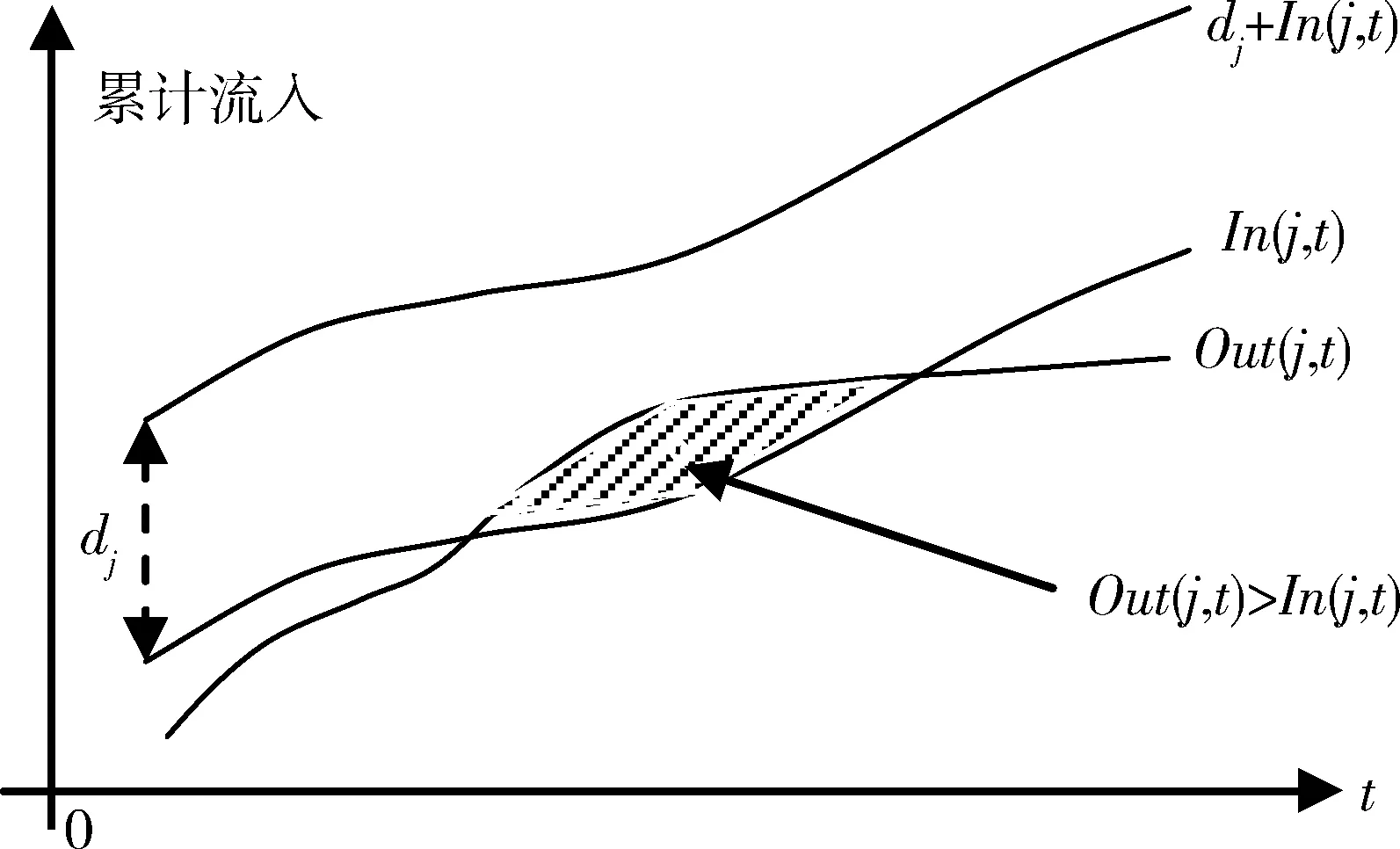
图2 需求量决策示意图

2.3 单车投放问题分析与描述
基于对单个投放点(投放区域)需求量的描述,单车的投放问题等价于如何在满足每个投放点基本需求的基础上,考虑到投放点间的车辆动态流转情况,最小化总投放量,并将总的投放量在各投放点上合理的分配。
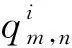
基于以上分析,我们主要研究以下三个方面的问题:
(1)基于现有的单车流转情况,若每天调度一次,满足现有需求的最小的单车投放量是多少?
(2)是否存在一次投放,不需要调度的投放方案,如果有,此时的单车投放量又是多少?
(3)对于企业而言,如何处理投放与调度间的关系,应该多投放、少调度还是少投放、多调度呢?
3 单车投放模型构建
3.1 每天调度一次的单车投放方案
3.1.1 模型构建
(1)在这种方案下,有用户使用单车的时段并不对单车进行调度(凌晨6点至次日凌晨1点),而是在鲜有用户使用单车的时段(凌晨1点到6点),利用卡车对单车分布情况进行统一调度[18],使单车恢复到每天开始的状态,假定该调度方案下,单车的总投放量为hsum1,结合前文关于不同时、空的单车数量变化规律,最小总投放量可通过以下的优化问题求解。
(1)
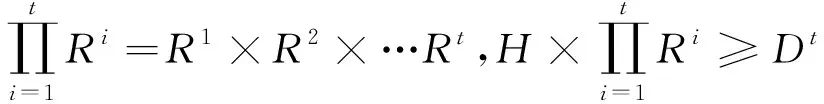
s.t.H×At≥Dt,(t=1,2…I)
(2)
3.1.2 解的性质分析
(1)解的存在性。由于现实中的投放点间都是连通的,不会存在孤立的单车投放点,因此,概率转移矩阵At>0(t=1,2…I)且不会出现全为0的列,对于任意t∈{1,2…I}所对应的Dt,由矩阵(向量)计算的公式:
(3)

(2)最优解与模型参数间的关系。此处的模型参数主要是指构建最优投放数量模型的时空粒度,对于最优解与时空粒度间的关系,我们用如下的命题1来描述。
命题1:随着时间和地点的细分,原优化问题的可行域将变小,对于目标函数求极小值的情况,最优的单车投放数量将可能上升。

综上所述,无论是时间还是空间上的细分,都是在原优化问题的基础上,增加约束条件。而对于约束优化问题,在原问题的基础上增加约束条件,会使可行解空间缩小,从而使优化的结果变差。本文构建的是目标函数最小化的优化模型,时空的细分将会使目标函数值变大,即单车投放量增加。
关于命题1的说明:命题1说明单车的投放量不仅取决于单车投放问题本身,还取决于研究投放问题的深入程度,这也是一个非常有趣的管理现象。当所获取的数据很丰富,可以进行很细致的时空细分时,根据优化模型得到的单车数量反而会上升。究其原因,其背后的逻辑是:时间数据越粗糙,在分析时越容易忽视(遗漏)一些需求,如一辆单车在一个较长的时间范围内可能在两个投放点间往返多次,粒度太大的时间或空间数据(这两个投放点可能合并为一个投放点)都无法准确地描述出这种需求;相反,时空粒度越小、越详细的数据,对需求的把握越准确,优化问题的求解结果也越好。因此,对于单车的投放与重新布局问题(Repositioning),通过对多个投放点进行聚类[27]以简化问题规模的方式会使空间粒度变大,尽管在算法上是可行的,但对于具体问题的求解精度还是有较大的影响。在现实中,数据的粒度与求解的复杂度也是需要权衡的问题。
3.2 一次投放、不进行调度的投放方案
3.2.1 模型构建
在构建优化模型之前,先引入如下两个引理。
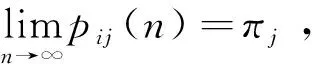
引理2(遍历性的存在性)[28]:设{X(n),n=1,2…}是具有s个状态a1,a2,…as齐次马氏链,若存在正整数n0,对于任意i,j,使pij(n0)>0,称该马氏链必是遍历的。且πj是方程
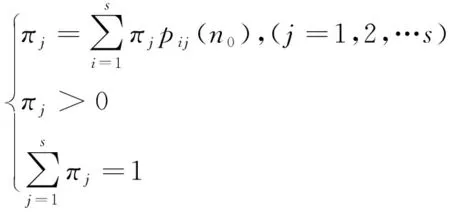

(4)

3.2.2 解的性质分析
由
等价于
(5)

3.3 实时调度的投放方案
3.3.1 模型构建
当车辆可以实时调度时(为简化分析过程,突出三类方案间对比关系,暂时先不考虑调度的成本,即车辆可以任意在空间上进行调度),记实时调度情况下,单车的最小投放量为hsum3,则hsum3可通过如下的优化问题求解:
(6)

(7)
3.3.2 解的性质分析

基于以上的分析,结合调度频率与单车投放数量间的关系,本文提出关于单车投放量的命题2如下。


4 案例分析
在现实中,很多共享单车公司的单车都有GPS定位,能够实现动态化地监测车辆数据、骑行分布数据,进而对单车做出全天候供需预测,为车辆投放和运维提供指引。本案例依据某共享单车公司所提供的1000辆单车在10个投放点间的骑行数据(1天内)进行分析,详细数据见附件1-骑行数据(案例数据源于2017年全国大学生数学建模大赛的竞赛题目,原始数据、过程数据、代码附录都可从https://pan.baidu.com/s/13pVw0feFzinRGFN8fN GHAA下载)。
4.1 状态转移概率矩阵的确定
通过对案例中车辆数据的初步整理和分析,可知1000辆自行车在各投放点的初始分布情况见附录中表1所示。
为统计计数方便,将1天的时间分为12个时段(A1到A2,每个时段120分钟),可以计算出在每个时段内,任意两个区域间的车辆流动情况、各区域车辆的流入和流出情况(按区域汇总)、在各时段开始时刻,各区域的车辆保有量(已出发的在途车辆,计入目的地区域),最终计算出不同时段各区域间的状态转移率,详见附录中的表2(计算过程见附件内容),其中每一列数据对应于一个10×10的状态转移矩阵。
4.2 各节点需求量的确定
基于案例数据,考虑到需求在时间上的分布情况,以2个小时为一个时间段,对每个投放点的单车流入(还车)情况和单车流出(用车)情况进行了统计(记录每5分钟单车的流入数量和流出数量),通过对统计数据进行非参数检验,根据原始检验结果(分析的数据及结果见附件-统计检验),整理得到关于流入数量和流出数据的检验结果分别见附录中的表3和表4所示。
关于表3和表4的说明:(1)由于时间段A1-A3对应于0-6点,此段时间没有车辆使用和还车数据,在用车规律和还车规律检验中未体现这段时间。(2)K-S非参数检验可以做正态分布、均匀分布、泊松分布和指数分布的检验,表中数据包含4位数字,每一位数字分别对应于不同分布的检验结果,0表示“保留原假设”,1表示“拒绝原假设”,如0101表示保留正态分布假设、拒绝均匀分布假设、保留泊松分布假设和拒绝指数分布假设。
从检验结果的总体规律可以看出,所有节点在不同时段的用车和还车频数情况都不能拒绝服从泊松分布的假设,有个别情况不服从正态分布,部分不服从均匀分布,绝大部分不服从指数分布。考虑到服务系统一般都服从泊松分布,基于假设检验的结果,本文用泊松分布来描述还车和借车频次的分布情况也是合理的。根据检验的结果,可整理得到不同投放点在不同时段上,用、还车的泊松分布参数见附录中表5和表6所示。
由泊松分布的性质[30],记还车频率In为服从均值为λIn的泊松分布,用车频率Out为服从均值为λOut的泊松分布,当服务水平要求为α时(案例中取α=95%),每个节点在各时段的需求为d,则In+d-Out服从均值为λIn+d-λOut的泊松分布(要求λIn+d-λOut>0,以满足服务水平的要求)。结合泊松分布的累积分布函数,求得各节点在不同时段满足服务水平为95%时的需求如附录中表7所示(Matlab计算代码见附件-需求计算)。
4.3 模型求解
按时段将需求表整理为12个需求向量Dt,t∈{1,2…,12}(前三个时段无需求变化,需求向量为0),利用MATLAB (R2016a)的yalmip工具箱,针对以下的三种情境建立优化模型并完成求解。
4.3.1 每天调度一次的单车投放方案
直接求解如下的线性规划问题(求解代码见附件-优化1),
(8)
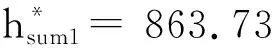
4.3.2 一次投放、不进行调度的投放方案
基于已有的状态转移矩阵,记一天中所有时段的状态转移概率矩阵的乘积为R12(精确到小数点后两位,详见附录中R12),由于R121=R122,n0=2时已达到稳定,可得:

0.12,0.11,0.10]
求解如下优化问题(求解代码见附件-优化2)
(9)
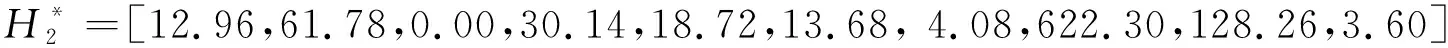
4.3.3 实时调度的投放方案
在前文基础上调整约束求解如下优化问题(求解代码见附件-优化3)
(10)

关于求解结果的说明:(1)论文中所呈现的数据均为精确到小数点后两位的数据,运用Matlab进行计算时,精度要更高。(2)由于投放需求的估计涉及到概率计算,会有大量小数(非整数)产生,在数据分析与处理时,为使处理过程更为流畅,也并未将“现实中的投放量为整数”作为限制条件,在考虑单车的实际投放量时,可参照模型求解的最优结果进行取整或小幅度上调投放量,以满足在各个投放点的取整要求。
案例研究的结果表明,案例公司的单车投放量过多,即使用车量最大的情境(一次投放、不进行调度),基于目前的需求情况,所研究的1000辆单车仍可以削减104(1000-896)辆,降幅达10.4%;如果引入适当的调度策略,单车投放量能节约136(1000-864)-377(1000-623)辆,降幅高达13.6%-37.7%。此外,在不同的调度情境下,最优的单车投放量在各节点的分布也有较大的差异。
5 结语
共享单车的过度投放已经给城市管理带来了严重的社会问题,文章引入服务水平的概念,充分考虑用车需求和还车需求的不确定性,通过分析服务水平与投放点需求量间的关系,从理论上给出了满足特定服务水平约束的投放点需求量应满足的条件,为需求量的确定指明了方向。在明确投放点需求量的基础上,基于马尔可夫过程描述单车数量分布的时空演化规律,根据不同的调度情境构建相应的优化投放模型,所构建的模型具有较好的适应性,可以根据现实需求调整时空粒度的大小,满足特定的计算精度。通过对模型的最优解的性质进行分析发现:(1)模型的时空粒度越小,越能捕捉(反映)真实需求,最优的单车投放数量也将越大。这也说明在现实中进行数据收集与分析时,必须要注意使用恰当的时空粒度。(2)单车的投放数量与运营调度频率负相关,调度频率越高,所需要投入的单车数量越少,并从理论上给出了单车投放数量的上限和下限。对于现实中的单车投放企业而言,如果想通过降低投放数量来降低单车投放成本,在不影响服务水平的情况下,就必须要增加运营调度的频率,使管理成本上升,反之也可以通过增加车辆投放量来缓解调度的压力。但为了保障服务水平、兼顾社会管理问题,单车投放数量应在理论给定的界限范围内。
此外,本研究仅立足于单个共享单车企业,从满足特定服务水平的角度,研究车辆的投放量问题。由于侧重点的不同,在本文中暂未考虑单车投放企业间的竞争,而竞争也是在客观上导致企业过度投放单车的重要因素。在后续的研究中,考虑企业间的竞争关系再优化单车的投放策略,也是非常有趣和值得关注的问题。

