基于球面距离的旅行商问题及其应用
吴皓华,曹 茜 (上海电力大学,上海 200090)
旅行商问题(Traveling Salesman Problem,TSP)可以概括为:无论是在平面还是在空间内,如何一次性用最短的路径走完所有节点,并从最末点回到出发点,同时所走的路径中只存在一个循环,不含任何子循环。
旅行商问题虽然是一个基础性问题,但是其对于问题处理的思维方式在其他问题的研究中也有重要的借鉴意义。而且基于其在工业和科学技术方面的重要应用,直到现在TSP及其衍生问题都始终被作为热门的研究对象。同时TSP作为公认的NP完全问题,其解法和答案的多样性说明了这个问题有待开发的巨大潜力。
1 旅行商问题
旅行商问题(TSP)的发展从未停止过,针对这个问题的传统解决思路是通过有限次的数学迭代计算来得出一个相对可行解。随着计算机技术的发展以及各种学科之间的交互加深,新的算法和对原算法的改进也就随之产生了。比如由戚远航和蔡延光等[1]提出的将初始化步骤混沌化从而可以得出小范围数据内的精确解和大范围数据内的优化近似解的混沌混合离散蝙蝠算法,以及Hui Yang、Li-shan Kang和Yu-ping Chen等人[2]将从最小跨距树中的相关数据归纳而成的基因库应用到基因算法之上来减小误差的基因库改良。这些算法和思路在最初设计时就借鉴了其他学科的内容,同时得益于先进计算设备的帮助,它们的处理对象可以是更加复杂和多样的内容。而算法真正体现价值的时刻就是能够脱离理论、应用于实际问题的时刻。比如程嘉、罗希和陆大明等人[3]在将TSP的计算范围从理论拓展到公交系统规划的过程中做出了贡献。
2 球面距离
在传统的旅行商问题中,距离计算都是基于欧几里得距离,本文则采用球面距离。球面距离的核心思想来源于球面三角学,作为非欧几何的一个重要组成部分,球面几何学对于天文学、航海学和地理学的贡献无法估量。
地理学上人为地依据赤道(即0°纬线)将地球分为南北半球,依据西经20°和东经160°两条经线将地球分为东西半球。此分法是按照将地球看作为一个标准的正球体,从地球球心出发,规定垂直和水平两个平面,然后将垂直平面按轴线逐渐翻动、水平面向上下平移成一组平行平面,随即就能在地球表面出现数条经纬线的步骤进行的。这样一来,地球表面就由这数条经纬线构成了一个坐标系。地球表面的任一位置都可以由一个维度和一个经度所组成的信息来表示。
于是,假设地球表面存在A、B两个位置,其坐标信息分别为A( xi, yi)、B( xj, yj),前者代表纬度、后者代表经度,同时用R表示近似看成正球体时的地球半径,则根据三角函数的内容,球面上两者间的距离可以表示为:
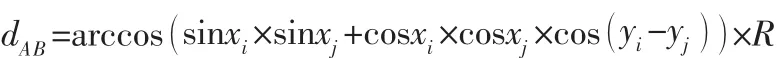
此时,dAB的大小就是球面上A、B两点之间的距离。
3 案例概述
自从第二次世界大战以来,美国就一直维持着数量庞大的军事基地,从本土到海外,这些军事基地分布于世界各地。以下是美国目前公布的部分军事基地坐标的其中25个(角度制的换算规则为:1°=60',1'=60″),罗列如下:
A.安德鲁斯空军基地:38°48'31.72"N,76°51'35.28"W(美国华盛顿哥伦比亚特区);
B.陆军刘易斯堡:47°4'57.21"N,122°35'2.78"W(美国华盛顿州);
C.廷克空军基地:35°25'29.94"N,97°23'29.92"W(美国俄克拉荷马州);
D.威洛格罗夫空军后备航空站:40°12'13.59"N,75°8'53.78"W(美国宾夕法尼亚州);
E.陆军本宁堡:32°21'37.75"N,84°58'8.85"W(美国佐治亚州);
F.斯特科空军基地:38°32'20.37"N,89°51'18.02"W(美国伊利诺斯州);
G.西点军校:41°23'30.32"N,73°57'26.95"W(美国纽约州);
H.坎贝尔堡101空降师司令部:36°38'20.56"N,87°26'58.37"W(美国肯塔基州);
I.霍洛曼空军基地:32°50'20.07"N,106°5'35.09"W(美国新墨西哥州);
J.基斯勒空军基地:30°24'26.09"N,88°55'26.79"W(美国密西西比州);
K.布兰丁陆军训练基地:29°56'16.71"N,81°58'47.63"W(美国佛罗里达州);
L.卡纳维拉尔角发射基地:28°35'11.35"N,80°39'6.68"W(美国佛罗里达州);
M.奇威斯特海军航空站:24°34'39.70"N,81°41'54.22"W(美国佛罗里达州);
N.小石城空军基地:34°54'38.12"N,92°8'56.40"W(美国阿肯色州);
O.新奥尔良海军航空站:29°49'41.99"N,90°1'32.46"W(美国路易斯安那州);
P.美陆军驻德国维斯柏顿第12航空旅:49°39'12.64"N,9°58'22.33"E(德国);
Q.冲绳第3陆战师基地:26°23'32.17"N,127°51'19.08"E(日本);
R.喀布尔机场空军基地:34°33'40.64"N,69°13'10.34"E(阿富汗);
S.安德森空军基地:13°34'29.41"N,144°55'19.91"E(关岛);
T.关塔那摩军事基地19°54'59.96"N,75°7'50.48"W(古巴);
U.常规军需品仓库51°28'15.58"N,1°24'11.53"W(英国);
V.迪戈加西亚美军基地7°18'53.88"S,72°25'6.18"E(驻印度洋);
W.玛那兹空军基地43°3'29.76"N,74°28'18.45"E(吉尔吉斯斯坦);
X.汉纳巴德空军基地:38°50'0.56"N,65°54'36.95"E(乌兹别克斯坦);
Y.乌代德空军基地:25°8'9.00"N,51°18'48.51"E(卡塔尔)。
假设需要给巡航飞机设计一条路线,从A出发且不重复经过任何已经路过的地点最后回到A,使得飞机巡航的总距离最小,下面把具体的航行路线设计出来。
4 利用Lingo求解
首先,需要进行单位统一。规定北纬数值为正值、南纬为负值,东经数值为正值、西经为负值。编写Lingo代码将原始信息中包含度、分、秒三个单位的数据统一转换为以度为单位的新数据。可以得到如下新的坐标数据(单位:度/°):

由于涉及到非平面的地球表面上的点,那么计算其上任何两点之间的距离就应该考虑使用球面距离公式。进一步,可以继续编写Lingo代码进行计算,但是这其中特别要注意,Lingo程序内的三角函数在计算时默认输入值的单位为弧度,所以在使用函数时需要注意将角度转化为弧度,于是可计算出每两点之间的距离见表1。
最后,在得到距离矩阵之后,就可以开始进行路线优化计算。编制路线优化的Lingo代码进行计算,结果如下:

表1 距离矩阵
最终计算出的最短里程见图1。
整合以上计算结果,可以作出如下路线规划:
A-D-G-U-P-W-X-R-Y-V-Q-S-B-I-C-N-F-H-E-J-O-M-TL-K-A,总的最短里程数为47 159.94千米,同时使用MATLAB绘制路线图见图2:
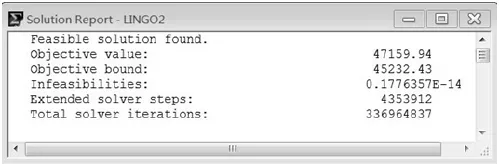
图1 最短里程的计算结果
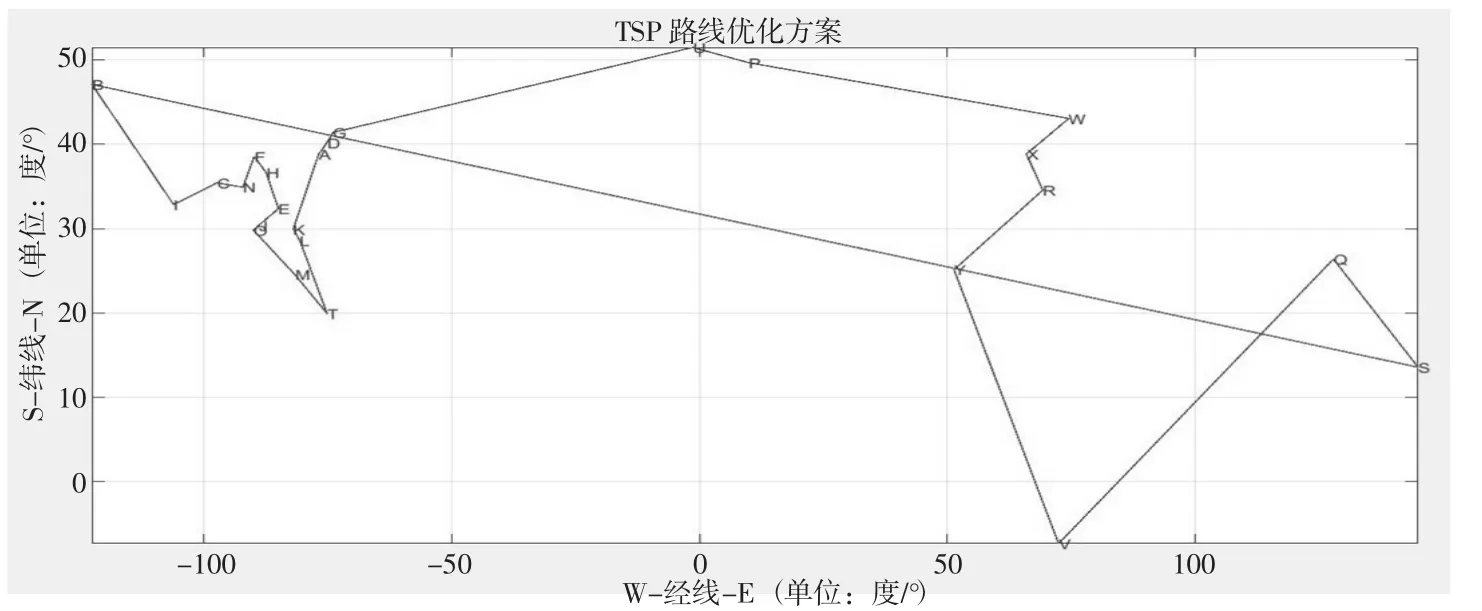
图2 优化路径
为了对计算结果进行验证,现在使用网页版百度地图对相关距离进行测距。由于在地图上手动取点精度不高,所以在地图上的测距数值与前文的计算结果存在微小的误差(单位:千米)。

表2 地图测距与计算结果的对比
在网页版百度地图上将各点的测距轨迹连接起来,就可以得到图像见图3:
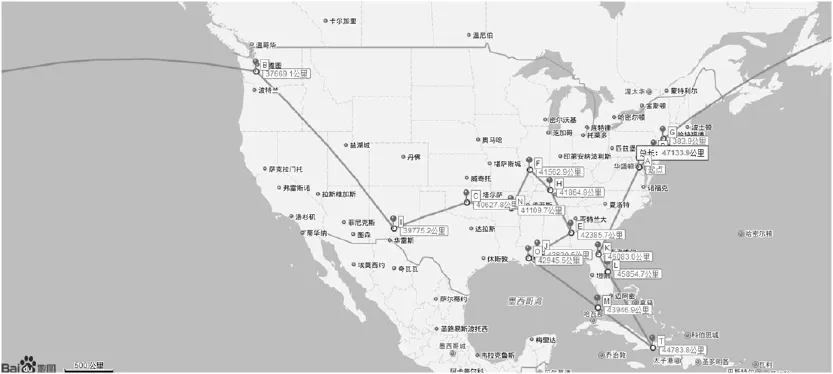
图3 地图测距轨迹(局部)
经过上述验证,结合实际数据表明,在允许一定误差的情况之下,以上的规划方案在理论上是正确有效的。
5 结束语
本文研究了基于球面距离的旅行商问题在实际案例中的应用,以美国目前公布的其中二十五个军事基地的坐标为例,对相关的问题建立了模型,并通过Lingo软件对该模型进行求解,得到了巡航飞机最优的航行路线,同时对计算结果进行了验证,证明了本文给出的求解方案是正确可行的。

