湘南桉树人工林地位指数建模

罗先权李柏海邓翔邹建文李蔚婷陈灵彭静饶红欣谭知虎

湘南桉树人工林地位指数建模

罗先权1#，李柏海1#，邓翔2，3＊，邹建文1，李蔚婷1，陈灵1，彭静1，饶红欣1，谭知虎1

(1.湖南省森林植物园，湖南 长沙 410116；2.中南林业科技大学林学院，湖南 长沙 410004；3.广东省恩平市农业技术推广服务中心，广东 恩平 529400)

以湘南桉树人工林为研究对象，探究立地因子与立地质量之间的关系。提取出湘南桉树人工林(邓恩桉和“常寒1号”林分)立地因子的5个主成分：土壤质地、林地有机环境、林地无机环境、坡度和坡向，方差贡献率依次是34.569%、17.120%、12.235%、11.319%和8.861%。通过因子分析法，筛选出非毛管孔隙度(Por_nc)、土壤有机质含量(C)、速效钾含量(K)、土层厚度(TH)、有效磷含量(P)、土壤酸碱度(pH)6个主导因子，并以此为自变因子建立7 a生湘南地区桉树人工林多元地位指数方程，逐步分析并进一步剔除了有效磷含量(P)和土壤酸碱度(pH)，最后拟合出方程：=12.619+0.053×+0.168×-0.021×+0.645×；其决定系数2为0.720，调整2为0.640，采用留一交叉验证法验证方程精度，得出均方根误差(RMSE)为0.606，估计精度(EA)为0.967，该方程可以适用于湘南地区培育7 a生桉树林分的地位指数预测。

湘南；桉树；择伐强度；生长量

湘南地区的桉树主伐年龄一般在5 a左右，但此时桉树的树高、胸径较小，木材多用作纸浆原料。但湘南地区成熟的桉树林分将带来更大的经济效益，科学合理的中大径材培育模式也能够兼顾生态效益。本研究基于国内外对湘南地区桉树近熟林和成熟林研究较少的现状，遵循选地适树的原则，主要选择7 a生的湘南地区桉树人工林分对象，分析其立地因子与立地质量的关系，探究湘南桉树人工林分的立地因子与立地质量之间的关系，结果可适用于该地区培育7年生桉树林分的地位指数预测，也为桉树大径材培育技术提供一些数据支持。

1 研究概况

1.1 立地质量的评价

1.1.1 立地质量评价指标

立地质量被定义为某一立地上既定森林的生产潜力，它与植被类型关联，并存在高低之别，包括气候、土壤与生物三大因素。而立地条件被定义为造林地上与林分生长发育相关的所有自然环境因子的综合。沈国舫等[1]认为二者在一定程度上相通用。立地质量评价是对立地的潜在生产力或宜林性进行判断和预测。目前，立地质量的指标已明确用地位指数(立地指数)表示[2]，地位指数通常被定义为某树种在基准林龄时的优势木平均高。

1.1.2 立地质量评价方法

有林地和无林地的立地质量评价需要采用不同的立地评价方法[3]。有林地的立地质量评价典型方法是依据优势木平均高与年龄关系来构建地位指数模型[4]、气候模型[5-6]、导向曲线[7]和广义代数差分模型[8]。无林地的立地质量评价通常是采用其他有林地立地的立地因子与优势木平均高之间的相关关系进行确定，一般是筛选出主导因子，进行多元地位指数建模[9-10]。

1.1.3 提取主导因子

在提取影响立地质量的主导因子过程当中，所应用的方法一般有：相关性分析、显著性检验、主成分分析、逐步回归分析和数量化理论分析等[8]。

在未来，立地质量评价将可能朝着如下几个趋势发展：①单因子变量向多因子综合分析转变；②单学科分析向多学科的综合应用转变；③从单纯的土壤肥力等因子到结合气候等多因子的定性定量多角度分析；④从单树种评价到多树种评价；⑤从仅考虑有林地的直接立地质量到对无林地的间接立地分析，并做出最优决策以遵循适地适树的原则[11-13]。

1.2 试验区概况

湘南地区包括湖南的郴州市、永州市和衡阳市部分地区，本研究的试验点位于永州市东安县、郴州市临武县和嘉禾县。东安县(110°59′ ~ 111°34′E，26°07′ ~ 26°52′N)全区总面积2 219.95 km2，地形以丘陵为主，西北略高于东南部，中部较为平坦；东安热量丰富，日照充足，年均气温17.0℃，最高气温38.5℃，最低气温7.50℃，年均降雨量为1 335 mm，无霜期300 d，年均日照数超过1 325 h。临武县(122°20′ ~ 122°47′E，25°07′ ~ 25°35′N)处岭南山脉东段北向，全县总面积1 383 km2，系湘水、珠江两河之源，地形西北向东南箕状下降倾斜，东山、西山和桃竹山为其骨架；县城平均海拔276 m；县境水热条件优越，年平均气温为17.9℃，平均降雨量1 421.8 mm。嘉禾县(112°1 ~ 112°35′4′E，25°26′ ~ 25°47′N)坐落在五陵山脉北麓，热量充足、雨水较为集中，春天温度变化较大、夏秋季节多干旱且严寒期短、暑热期长；年均气温18.3℃，平均日照时数1 443.2 h，年平均降水量1 408.8 mm，每年的无霜期约为296 d。

2 研究方法

2.1 试验方法

2.1.1 标准地的调查和采样

在永州市东安县7 a生“常寒一号”桉树人工林分中设置15个标准地；在郴州市嘉禾县和临武县的3、4、5、6和7 a邓恩桉林分中分别设置了标准地3、3、4、4和4个；总共33个标准地。所有标准地均为20 m × 20 m，面积400 m2。之后进行样地调查。所有标准地的基本调查因子都包括：地形因子和林木生长量(树高、胸径、冠幅、枝下高)。

部分标准地根据试验设计还需进行土壤采样，调查林地土壤的理化性质：

每个标准地挖1个土壤剖面。记录土层厚度(土层厚度1.5 m为最大调查深度，超过1.5 m则标记为>1.5 m，其他如实登记)。利用环刀法，对每个土壤剖面的不同厚度层1、2和3层(0 ~ 20、20 ~ 40、40 ~ 60 cm)进行采样，每层1个环刀；并在环刀取样的同时，用土壤袋对1和2层的土壤进行采样，每层取土样约200 g。将取好的环刀和土样带回实验室进行土壤理化性质测定。环刀样品用以测定林地土壤的物理性质，包括土壤容重、孔隙度(总孔隙度、毛管孔隙度和非毛管孔隙度)、持水量(饱和持水量、毛管持水量和田间持水量)等指标。土壤袋样品用以测定林地土壤的化学性质，包括pH值、有机质含量、水解氮、有效磷和速效钾等指标。

2.1.2 数据处理

2.1.2.1 立地因子数据的整合

因子分析本质是一种多元降维处理，其分析过程不涉及地位指数，故作为因子分析的对象的标准地可以是不同林龄的。整理作为立地分析试验对象的33个标准地(其中桉树7 a生标准地19个，6、5 a生标准地各4个，4、3 a生标准地各3个)的以下立地因子数据：坡度(SL)、坡向(Asp)、坡位(Pos)、土层厚度(TH)、土壤容重(pb)、总孔隙度(Por)、毛管孔隙度(Por_c)、非毛管孔隙度(Por_mc)、饱和持水量(W)、毛管持水量(W_c)、田间持水量(W_f)、pH值(pH)、有机质含量(C)、水解氮(N)、有效磷(P)和速效钾(K)。由于所有样地的海拔高度(EL)相近，故本研究暂不探讨EL与立地质量的关系。

其中土壤理化性质分厚度层整理(0 ~ 20、20 ~ 40、40 ~ 60 cm层分别记为1、2、3层)。理化性质先均取1、2层平均值作为立地因子变量并进行因子分析。

将每个标准地树高最高的5株树定为优势木，在进行因子调查时，该林龄的5株优势木的平均树高(Ht)作为此时评价该桉树人工林立地质量的指标。

2.1.2.2 部分立地因子数据的量化及粗化处理

为了方便研究，需要对定性因子进行量化处理；而为了提高研究结果的适用度，需要对某些无法精确测定的定量因子进行粗化处理。标准见表1。

表1　因子粗化处理表

2.2 数据分析方法

2.2.1 主成分的提取及命名解释

将所有立地因子输入SPSS19.0分析软件。利用因子分析法提取主成分，选取特征值>1的所有公共因子ƒi作为主成分。观察旋转后的公共因子载荷矩阵，此时作为主成分的公共因子的含义较为清晰，故能以此为根据进行命名解释。

2.2.2 主导因子的筛选

一般情况下，较为重要的立地因子变量会在某个主成分的旋转因子载荷上拥有较大的值，但如果仅依据该最大值判断该变量对综合立地情况的解释能力，则可能无法兼顾该变量在其他主成分上的信息。为避免信息的过多丢失，本研究根据姚雪玲等[14]的研究方法，引入变量Norm；通过计算其变量值ik，从各个主成分ƒ1-k上载荷绝对值大于0.5的立地因子中，选择ik变量值最大者以及该最大变量值10%范围内的其他立地因子，进入该主成分的主导因子待定组1~k；各个待定组内立地因子相关性显著的，则取ik值最大的立地因子作为代表该主成分的主导因子；待定组内相关性不显著的，即不能被其他因子所代表，也要被筛选为该主成分的主导因子。Norm值计算公式为：

ik：第i个立地因子变量在k 个主成分上的综合荷载，即Norm值；

ik：第i个立地因子变量在第k 个主成分上的荷载；

k：是第k个主成分的特征值。

2.2.3 利用主导因子变量构建多元线性地位指数方程

利用SPSS19.0数据分析软件进行多元线性回归分析，分析的对象为19个7 a生的桉树人工林标准地。将筛选出来的主导因子变量作为自变量，优势木平均高(Ht)作为因变量，输入软件，并采取向后逐步筛选策略，拟进一步控制主导因子的个数，从而达到精简回归方程同时又能提高方程拟合调整2的目的。余下不适合剔除的立地主导因子变量作为方程的最终自变量组，由此回归出来的方程为最终的多元线性地位指数方程。

2.2.4 多元线性地位指数方程的精度检验

由于该立地分析试验7 a生标准地数量较少，只能进行小样本的回归分析，故在对拟合出来的回归方程进行检验时，采用留一交叉验证法。

留一交叉验证法是先在回归对象的所有19个标准地中留出1个，另外的18个标准地的变量重新进行回归，只选择第(5)步最终确定下来的立地主导因子，采用强制进入策略(所有立地主导因子强制输入回归方程)，拟合出1个检验回归方程，再用留出该标准地的观测变量去验证相应的检验回归方程。如此重复19次，直到每个标准地都被留出去验证过另外18个标准地回归出的方程。

通过留一交叉验证法，可以得到19次验证的均方根误差(RMSE)和估计精度(EA)，其计算公式为：

yi：留出的检验标准地地位指数的实测值；

ŷi’：检验标准地立地因子变量代入临时回归方程计算得到的模拟值；

`y：检验标准地地位指数的实测值均值；

k：回归样本的个数；

n：检验样本的个数。

最终拟合出来的回归方程的RMSE和EA即为这19次检验回归方程验证的RMSE和EA的均值。

3 结果与分析

3.1 提取主成分并进行命名解释

将坡度(SL)，坡向(Asp)，坡位(Pos)，土层厚度(TH)，第1、2层的土壤容重(pb)、总孔隙度(Por)、毛管孔隙度(Por_c)、非毛管孔隙度(Por_mc)、饱和持水量(W)、毛管持水量(W_c)、田间持水量(W_f)、pH值(pH)、有机质含量(C)、水解氮(N)、有效磷(P)和速效钾(K)进行因子分析发现相关矩阵无法通过Kaiser-Meyer-Olkin检验(KMO)和巴特利特球度检验(Bartlett)；而将土壤容重(pb)和总孔隙度(Por)改为第1、2、3层的平均值后，结果KMO度量为0.703，Bartlett近似卡方为714.669，<0.01，说明这些因子变量较适合做因子分析。故后续的pb和Por变量值采用第1、2、3层土壤样品的平均值进行因子分析。

由表2可知部分立地因子之间的相关系数很高，特别土壤物理性质的各个因子间、土壤有机质含量(C)和土壤水解氮含量(N)之间的相关性，其相关系数的绝对值基本都超过了0.5，说明这些因子间的多重共线性很明显。如果只根据相关系数来筛选主导因子，很可能会对后面的回归分析的参数估计造成阻碍，导致回归参数预估不准确，甚至回归模型不可用。但从另一个角度来看，各因子间存在较强的线性关系，则更容易提取公共因子，适合进行因子分析，这点通过KMO和Bartlett的检验结果也可印证。

该16个立地因子进行线性组合，变换为16个公共因子ƒ1~16，并采用最大差分法对因子载荷进行旋转。

表2　立地因子相关性矩阵

注：表中加粗标注表示相关性达到显著程度

表3列出了初始公共因子解的特征值和方差贡献率情况、提取特征值大于1的公共因子、正交旋转载荷矩阵后因子解的特征值和方差贡献率情况。将特征值大于1的公共因子(前5个)提取出来作为主成分。观察正交旋转后的方差贡献率可知，5个主成分的方差贡献率分别为34.569%、17.120%、12.235%、11.319%、8.861%，累积达到了84.103%，说明这5个主成分可以解释原有所有立地因子大部分的总方差，经过因子分析后丢失的信息不多，结果较为理想。

表3　公共因子解释原有因子总方差的情况

由表4可知，经过正交旋转之后，这5个主成分在更少的立地因子上存在高载荷值，这使得主成分的含义更为清晰。可将绝对值大于0.5的载荷值加粗标记出来进一步分析。

在第1个主成分上，土壤容重(pb)、总孔隙度(Por)、毛管孔隙度(Por_c)、非毛管孔隙度(Por_mc)、饱和持水量(W)、毛管持水量(W_c)、田间持水量(W_f)等土壤物理性质的载荷绝对值均大于0.6，其他立地因子载荷明显较小，所以可以把第1个主成分解释为林地的土壤质地。在第2个主成分上，土壤有效氮含量(N)和有机质含量(C)存在很大的载荷值，其他立地因子载荷明显较小。而在第3个主成分上，坡位(Pos)、土层厚度(TH)、土壤pH值(pH)的载荷绝对值大于0.6，其他立地因子载荷明显较小。通常评价土壤的肥沃程度需要从土壤的养分情况、耕层薄厚和酸碱环境等几个方面着手，第2主成分代表了土壤的养分情况，而第3个主成分则代表了耕层薄厚及酸碱环境。故可以将第2主成分命名为土壤有机环境，第3个主成分命名为土壤无机环境，二者共同代表着土壤的肥沃状况。

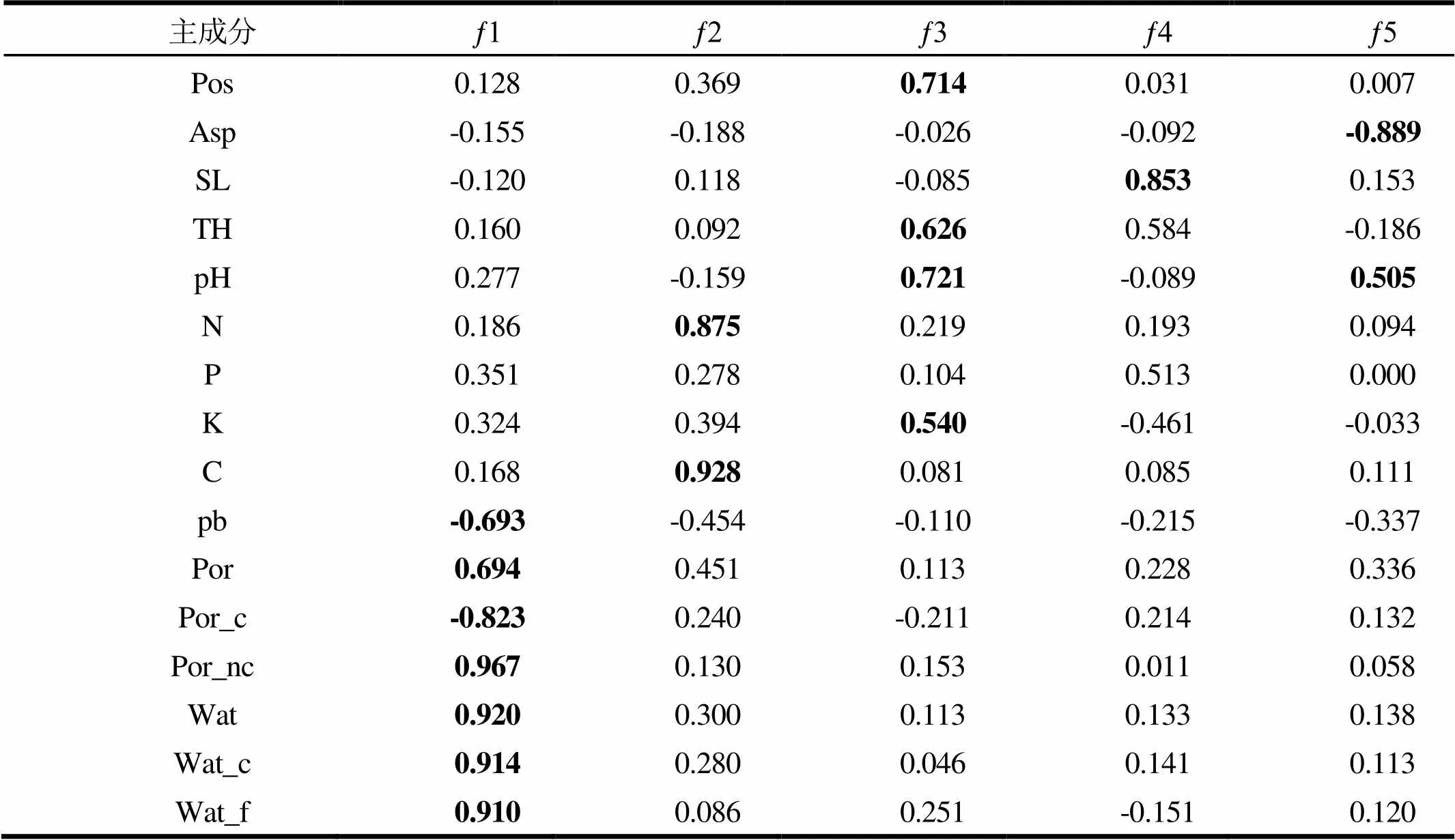
表4　主成分旋转因子载荷矩阵

注：表中加粗标注的表示该载荷值的绝对值达到了0.5以上

而在第4和第5主成分上载荷最高的分别是坡度(SL)和坡向(Asp)，绝对值均达到了0.85以上，明显高于其他因子，可将第4和第5主成分分别解释为林地坡度和林地坡向。

3.2 筛选出主导立地因子

引入变量Norm，其变量值为ik，通过公式计算出了各个立地因子的得分值ik，即第i个立地因子变量在k个主成分上的综合荷载(表5)。表中各主成分列出的立地因子得分值ik为载荷值>0.5的立地因子。其中加粗标注的为该主成分最高得分值10%范围内的所有得分值，即进入主导因子待定组1~5。通过观察本节前面表3.1中各立地因子之间的相关性，筛选出最后可以作为主导因子的立地因子，并在表中下划线标注。

第1主成分ƒ1中，进入主导因子待定组F1的因子有Por_nc、Wat、Wat_c、Wat_f，但这几个因子之间的相关性全为显著，所以只选择得分值ik最大为2.30的非毛管孔隙度(Por_nc)为主导因子。主成分ƒ2中，进入组F2的因子有N和C，但两因子的相关性显著，所以只选择得分值最大为1.60的土壤有机质含量(C)成为主导因子。主成分ƒ3中，进入组F3的因子有TH、pH和K，K与pH相关性显著，而与TH相关性不显著，所以选择得分值最大为1.40的速效钾含量(K)和得分值为1.26的土层厚度(TH)成为主导因子。主成分ƒ4中，进入组F4的因子有SL、TH和P，TH与SL相关性显著，而与P相关性不显著，所以选择得分值最大为1.26的土层厚度(TH)和得分值为1.18的有效磷含量(P)成为主导因子。主成分ƒ5中，进入组F5的因子只有pH，其得分值为1.37，故筛选成为主导因子。

最后筛选出的主导因子为非毛管孔隙度(Por_nc)、土壤有机质含量(C)、速效钾含量(K)、土层厚度(TH)、有效磷含量(P)、土壤酸碱度(pH)。

3.3 多元地位指数方程的建立与拟合

本研究采用的方程模型为多元线性方程。因变量是地位指数Ht，其变量观测值选择优势木平均高Ht。自变量是上节筛选出的6个主导因子。建立如下初模型：+b×+b×+b×+b×+b×+b×，其中，a为常量；b1、b2、b3、b4、b5、b6为主导因子的系数参量。

将6个主导因子输入回归分析软件，综合考虑调整2、回归方程显著性、变量的多重共线性等，采用向后筛选策略进行逐步回归，进一步控制变量的个数，建立并拟合一个更为简洁却不失精度的方程。

由表6可知，初始回归方程自变量有6个，进行拟合后决定系数2为0.730，调整的决定系数调整2为0.595。第1步逐步回归，剔除了自变量P，发现2下降了0.001，但调整2却上升到了0.625，同时偏F检验概率为0.835，这表示变量P的偏回归系数与零无显著差异，其对地位指数的线性解释没有显著贡献，须剔除。第2步逐步回归，剔除了自变量pH，2下降了0.009，但调整2却上升到了0.640，同时偏F检验概率为0.515，这表示变量pH的偏回归系数与零无显著差异，其对地位指数的线性解释无显著贡献，须剔除。最终分析保留了变量K、TH、C、Por_nc和常量a。

表5　立地因子在各主成分的综合荷载值

注：其中加粗标注的为该主成分最高得分值10%范围内的所有得分值

表6 逐步回归过程

注：(1)初始自变量：a, K, P, TH, pH, C, Por_nc；(2)因变量：Ht；(3)最终变量：a, K, TH, C, Por_nc

表7为最终的回归分析结果。经过第2步逐步回归分析后的回归系数即为最终方程的回归系数。多元线性地位指数方程为：12.619+0.053×+0.168×﹣0.021×+×，其中：因子Por_nc为无纲量，C的单位为g·kg-1,K的单位为mg·kg-1，TH以土层厚度<40 cm为1、40 ~ 60 cm为2、60 ~ 80 cm为3、80 ~ 100 cm为4、100 cm以上为5，Ht单位为m。式中涉及到林分土壤理化性质的变量均为0 ~ 20 cm和20 ~ 40 cm测定值的均值。

3.4 方程精度检验

对19个样地回归出来的方程进行精度检验，采用留一交叉验证，结果见表8。最终回归方程的决定系数2为0.720，调整2为0.640，均方根误差(RMSE)为0.606，估计精度(EA)为0.967。

表7 逐步回归分析结果

表8 回归方程精度验证

4 讨论

有效磷(P)在第1、2、4主成分上的载荷值为中等，速效钾(K)在第1、2、3、4主成分上载荷值较平衡。这两个因子在任何一个主成分上的载荷都不高，若只根据各个因子在单个主成分上的载荷值绝对大小，取较大者作为主导因子，则这两个因子将会被忽略。但实际上这两个因子都被筛选成为了主导因子，说明只根据单个主成分的载荷确定主导因子结果并不精确。必须要考虑各因子的综合载荷，才可以更准确地找到主导因子。

坡向(Asp)与坡度(SL)两个立地因子对桉树林分的地位指数影响也较大，但湘南地区多为丘陵地带，海拔起伏落差较小；而且为方便主伐运送，湘南桉树人工林一般建立在坡度较小的宜林地上。所以，本研究的试验标准地坡度均不大，这导致试验数据中坡向及坡度与地位指数的偏相关性较弱，最后该两个因子并没有被筛选出来成为主导因子。

5 结论

(1) 通过主成分法分析湘南桉树人工林的结果可知，第1主成分为林地土壤质地，第2主成分为林地有机环境，第3主成分为林地无机环境，第4主成分为坡度，第5主成分为坡向；这说明在湘南地区桉树现有人工林中，林地的土壤各项指标因子对林分的地位指数有着举足轻重的控制作用。

(2) 采用主成分分析结果筛选主导因子，若只根据单个主成分的载荷确定主导因子结果并不精确；必须要考虑各因子的综合载荷，才可以更准确地找到主导因子。最后筛选出的主导因子有非毛管孔隙度(Por_nc)、土壤有机质含量(C)、速效钾含量(K)、土层厚度(TH)、有效磷含量(P)、土壤酸碱度(pH)。

(3) 主导因子建立的多元地位指数方程，采用逐步回归法最终确定为：12.619+0.053×+0.168×﹣0.021×+0.645×；其决定系数2为0.720，调整2为0.640，采用留一交叉验证法验证方程精度，得出均方根误差(RMSE)为0.606，估计精度(EA)为0.967。

[1] 沈国舫,翟明普.森林培育学:第2版[M].北京:中国林业出版社,2011.

[2] SABATIA C O , BURKHART H E . Predicting site index of plantation loblolly pine from biophysical variables[J]. Forest Ecology and Management, 2014, 326:142-156.

[3] 郭艳荣,刘洋,吴保国.福建省宜林地立地质量的分级与数量化评价[J].东北林业大学学报,2014,42(10):54-59.

[4] 孟宪宇.山杨次生林地位指数表编制方法的研究[J].北京林业大学学报,2001,23(3):47-51.

[5] WEISKITTEL A R, CROOLSTON N L, RADTKE P J. Linking climate, gross primary productivity, and site index across forests of the western United States [J]. Canadian Journal of forest Research,2011,41(8):1701-1721.

[6] SHAMA R P , BRUNNER A , EID T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway[J]. Scandinavian Journal of Forest Research, 2012, 27(7):619-636.

[7] 郑聪慧,贾黎明,段劫,等.华北地区桂皮栋天然次生林地位指数表的编制[J].林业科学,2013,49(2) :79-85.

[8] LAUER D K. KUSH J S. Dynamic site index equation for thinned stands of even-aged natural longleaf pine[J]. Southern Journal of Applied Forestry, 2010, 34(1) :28-37.

[9] 亢新刚.森林经理学[M].北京:中国林业出版社,2011.

[10] 迟健,李桂英,陈家明,等.浙江省马尾松人工林立地质量的数量化研究[J].林业科学研究,1995,8(3) :303-308.

[11] 郭艳荣,吴保国,刘洋,等.立地质量评价研究进展[J].世界林业研究,2012,25(5):47-52.

[12] 徐罗.天然林立地质量评价[D].北京:北京林业大学,2014.

[13] 杨文姬,王秀茹.国内立地质量评价研究浅析[J].水土保持研究,2004,11(3):289-292.

[14] 姚雪玲,傅伯杰,吕一河.黄土丘陵沟壑区坡面尺度土壤水分空间变异及影响因子[J].生态学报,2012,32(16):4961-4968.

Effects of Selective Cutting Intensity on the Growth ofPlantations in Southern Hunan

LUO Xianquan1, LI Bohai1, DENG Xiang2,3, ZOU Jianwen1, LI Weitin1,CHEN Ling1,PENG Jing1, RAO Hongxin, TAN Zhihu1

(1.2.3.)

Taking 7-year-oldplantation in southern Hunan as the research object, explore the relationship between site factors and site quality.Five principal components of site factors of Eucalyptus plantation in southern Hunan were extracted(and "Changhan No. 1"): soil texture, forest nutrition, soil thickness, slope and aspect. The variance contribution rates were 34.569%, 17.120%, 12.235%, 11.319% and 8.861%, respectively. Six dominant factors, namely, non-capillary porosity (Por_nc), soil organic matter content (C), available potassium content (K), soil thickness (TH), available phosphorus content (P), soil acidity and alkalinity (pH), were screened out by factor analysis method, and use this as the self-variation factor to establish the multi-position index equation of 7a eucalyptus plantation in southern Hunan. And the available phosphorus content (P) and soil acidity and alkalinity (pH) were further eliminated by step analysis. At last, the equation was fitted:=12.619+0.053×+0.168×-0.021×+0.645×.Its determinant coefficient2was 0.720, adjusted2was 0.640, and the root mean square error (RMSE) was 0.606, and the estimation accuracy (EA) was 0.967。It can be used to predict the site index of 7-year-oldplantation in southern Hunan.

Southern Hunan;; selective cutting intensity; growth

S758.5+7

A

10.13987/j.cnki.askj.2019.04.001

国家重点研发计划课题“桉树大径材定向培育技术”(2016YFD0600502);湖南省外国专家局引智示范项目“耐寒桉树大径材推广示范”；湖南林业科技计划项目“耐寒桉树大径材高效培育技术研究”(XLK201722)

罗先权(1964— )，男，高级实验师，主要从事林木育种、林下药用植物开发、森林生态、速生丰产林培育研究，E-mail:284684186@qq.com

李柏海(1970— )，男，研究员，主要从事耐寒桉树研究与推广，E-mail: libohai1970@163.com

#为并列第一作者

邓翔(1994— )，男硕士，主要从事森林培育学研究及农林生产技术工作，E-mail:3250073612@qq.com