基于人工神经网络模型的岩石特性预测
陈晓君, 陈小根, 宋 刚 , 陈根龙
(1.中国地质科学院勘探技术研究所,河北 廊坊 065000; 2.北京科技大学土木与资源工程学院,北京 100083)
0 引言
神经网络是解决许多实际问题的有力技术,它可以作为一个直接代替自相关分析、线性回归、三角函数、多元回归等的统计分析方法[1]。ANN在岩石力学上的应用并不新鲜。例如,葛宏伟等[2]在研究岩石性质时采用了人工神经网络与遗传算法。Sirat和Talbot[3]利用ANN在瑞典东南部的Aspo硬岩石实验室(HRL)对水晶岩石不同裂缝的模式进行了识别、分类和预测。Sonmez等人[4]通过使用多输入参数方法构建了一个人工神经网络模型,以预测完整岩石的弹性模量,并提出了一个基于岩石质量等级(RMR)的经验公式,用于确定岩体的变形模量。魏丽萍[5]在开发利用人工神经网络研究岩石力学性质中发现,使用ANN构建这些模型比使用传统的统计技术更准确。Zborovjan和Miklusova等人[6-7]利用傅里叶变换进行了钻进中的声音识别研究,通过钻井的声学信号控制岩石破碎过程,取得了成功。由Vardhan等人[8]尝试通过在实验室规模上使用jackhammer钻机钻进过程中的声级水平来确定岩石或岩体性质(如压缩强度)的有效性,其中所施加的推力可以随钻凿垂直孔而变化。本研究也利用钻进过程中钻进参数和产生的声级水平建立人工神经网络模型预测岩石性质。
1 岩石物理分析
岩石单轴抗压强度是指岩样在单位标的压力下的极限粉碎强度,用σc表示。在实验室利用单轴抗压强度仪器来测定岩样σc的大小,将岩样固定在压力机的上下板之间,然后通过加压直至岩样破坏,压力表的值即为岩样的单轴抗压强度值。
施密特回弹数SPN,是通过计算施密特回弹锤回弹次数来测量岩石材料的硬度。结果很容易处理,它可以快速转换为最广泛使用的σ值,简单,快速。SRN的一些常见应用主要引用自Singh等人[9]地下大规模原位强度估算,而Janach和Merminod[10]将其应用在岩石磨蚀性的研究中。
岩石的密度分为天然密度和干密度,由岩石的含水状态决定,而岩石密度本身是与组成岩石的矿物成分和结构有关,尤其对那些特定岩石类型的组成成分非常敏感。岩石密度的测定方法比较传统,都是测出岩石的体积V以及岩石试样烘干后的质量m,然后计算出岩样的密度。
岩体在轴向拉应力作用下产生破坏的瞬间,在岩体单位面积上承受的最大拉力为岩体的抗拉强度,用στ表示。通常在实验室测定岩石的抗拉强度,由于许多微裂隙介质的存在,导致岩石试块在加工时具有易变性,而且实验环境也不容易控制,所以往往得到的岩石抗拉强度实验值与实际值相比,具有较大的偏差。对此,相关专家也进行了大量探讨与实验,力求找到一种比较稳定的实验方法来测定岩石的抗拉强度。
本研究将利用实验数据,将岩石的物理性质和钻进过程中产生的等效声级联系起来,找到它们之间的相关性。并通过人工神经网络建立基于等效声级的岩石性质预测模型,并对模型性能进行评价。
2 建立人工神经网络模型
2.1 多层感知器(MLP)模型
多层感知器(MLP)是一种常用的网络结构,它包含一个输入层、一些隐含层和一个输出层。在MLP中,输入和偏差项的加权总和通过一个传递函数传递到激活级别,以产生输出,而单元被安排在一个称为前馈神经网络工作的分层前馈拓扑结构中。隐含层和神经元的数量也是神经网络运行的一个重要参数。使用单个隐含层以最大化管理效率且总误差最小化。而且,正如Hornik等[11]所述,一个隐含层足以使ANN近似任何函数和任意给定的精度。使用不止一个隐含层可以导致大量的局部极小值并使训练变得困难。因此,不分析使用多个隐含层的影响。
不同的训练功能可以用来训练网络从特定的输入到特定的目标输出。当每个输入应用到网络时,将网络输出与实际目标值进行比较,并计算出误差。通过修改网络权重和偏差,将网络输出与实际输出之间的误差最小化。我们的目标是将均方误差(MSE)最小化。
(1)
式中:t(k)——实际值;a(k)——网络值;Q——期数。
当MSE低于预定值或已达到的最大期数,训练过程停止。然后利用输出和期望输出进行误差计算,将得到的误差值原路径反馈到网络中,并用于以迭代减小误差的方式调整权重。设置最小均方误差为10-4,最小梯度为10-5,最大期数为2000。如果满足上述条件,训练过程将停止。对于每一种训练算法,首先进行了一些试验,以确定隐含层中神经元的数目。均方误差最小的神经元数目被选择为隐含层神经元的最佳数目。
2.2 ANN模型
基于MLP利用试验数据建立了人工神经网络模型。在所有数据中,训练中使用了大约70%,其余的数据用于测试模型。空气压力、钻头直径、推力、钻进速率和A计权等效声级分别作为输入参数。这些输入参数覆盖了所研究的整个问题域,并在预测模型中是有效参数。岩石的特性如强度、干密度,回弹数和τ,为模型的输出参数。
为了确保每个输入参数在人工神经网络中提供相等的贡献,对模型的输入进行预处理并缩放到一个公共的数值范围(0,1)。在隐含层和输出层间有使用sigmoid激活函数的三个隐含层的网络。图1显示了这一人工神经网络模型的示意图。
3 结果与分析
3.1 实验数据
为了利用钻进过程的声级估计岩石参数,需要开展岩石钻进声响响应试验研究。针对10种不同岩性岩石开展了冲击钻进试验,表1中列出了10种岩石的基本物理力学参数及其在钻进过程中的等效声级[3]。
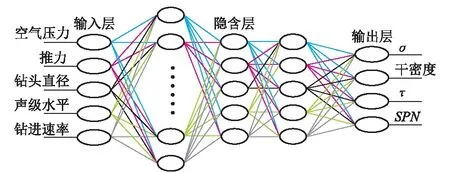
图1 3个隐含层的神经网络结构Fig.1 Neural network structure of three hidden layers
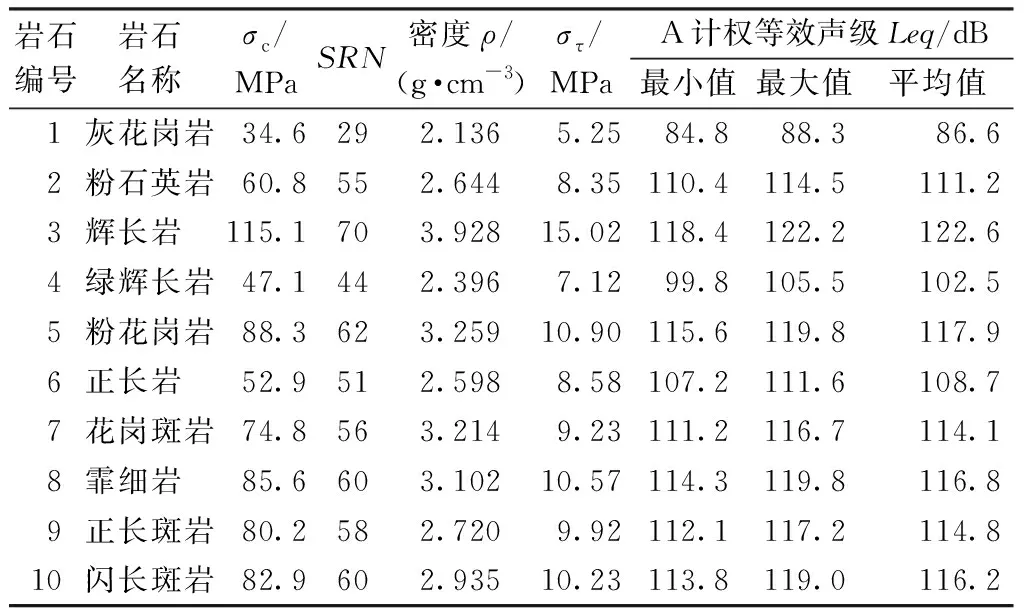
表1 钻进过程获得的岩石性质的统计值和等效声级值Table 1 Statistical values and equivalent sound level values of rock properties obtained during the drilling process
在不同钻头直径和不同的推力组合下测量的声级与不同岩石样品的基本物理参数(单轴抗压强度σc、施密特回弹数、岩石密度ρ、抗拉强度στ)之间的关系如图2~5所示。
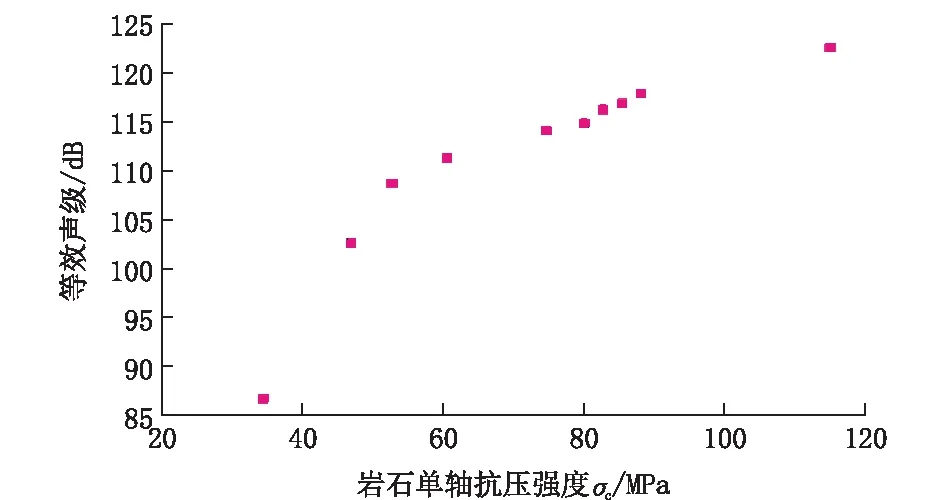
图2 抗压强度与等效声级Fig.2 Compressive strength and equivalent sound level
通过岩石性质参数与钻进过程的等效声级关系散点图可以看出,岩石的性质参数和等效声级之间具有较好的相关性。具体来说,除了施密特回弹数与等效声级之间是线性关系之外,其余3个参数与等效声级之间都是指数函数关系。即等效声级随着σc、ρ、στ的增大而呈指数增大的趋势,随施密特回弹数增大而又变现为线性增大的趋势。这些规律为研究钻进过程中的声学信息在岩石特性识别上建立了理论基础。
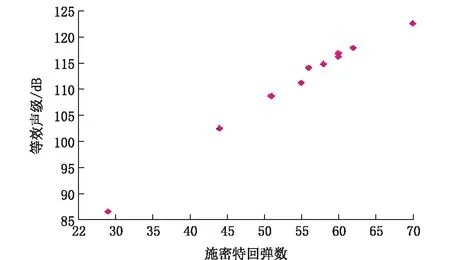
图3 施密特回弹数和等效声级Fig.3 Schmidt rebound number and equivalent sound level
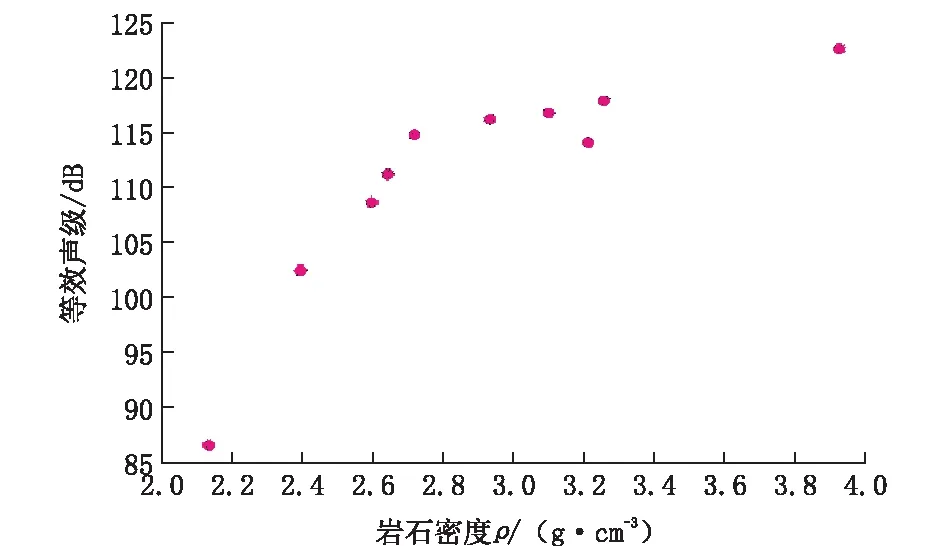
图4 密度和等效声级Fig.4 Density and equivalent sound level
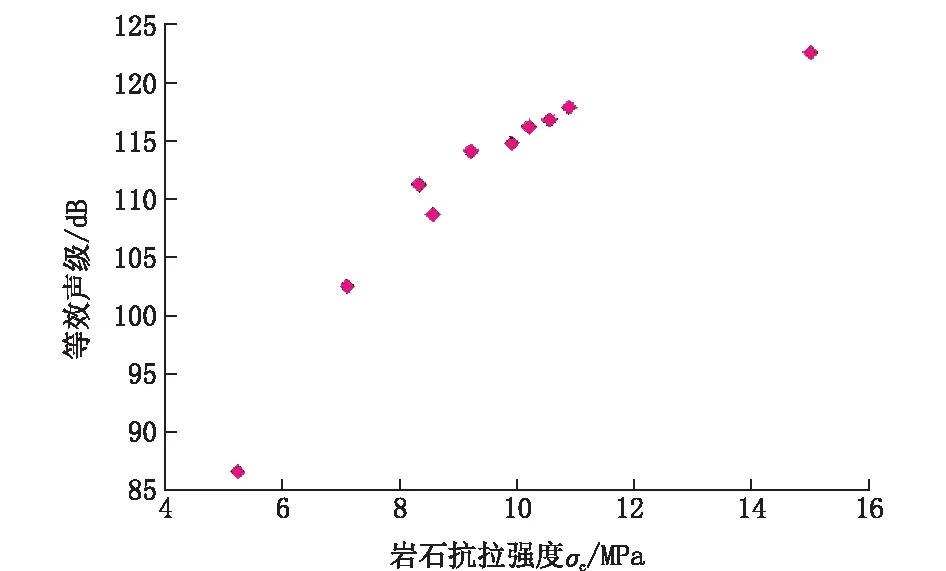
图5 抗拉强度和等效声级Fig.5 Tensile strength and equivalent sound level
3.2 最佳网络结构建立
MLP网络采用Matlab神经网络工具箱实现。该网络使用4种不同的BP训练算法即弹性BP算法(trainrp),比例共轭梯度算法(traincgf),基本梯度下降算法(traingd)和Levenberg-Marquardt算法(trainlm)。为了开发一种基于概括能力强、结构紧凑的最佳MLP结构,比较了不同的训练算法。
表2给出了使用不同训练算法的网络的体系结构和性能。很明显,从表2可以看出L-M训练算法收敛速度、期数、MSE值比其他训练算法更有优势。图6显示了采用L-M算法过程MSE与隐含层中神经元数量的变化。从图6可发现,对于此模型,当隐含层神经元的数量是5时,MSE为0.00015528,它随着神经元的数目的增加而减少,在神经元数目为30(13∶10∶7)时,达到一个最低值0.000101,此后增加神经元的数量,MSE又逐渐增加。因此,采用最佳MLP配置为5∶13∶10∶7∶4。
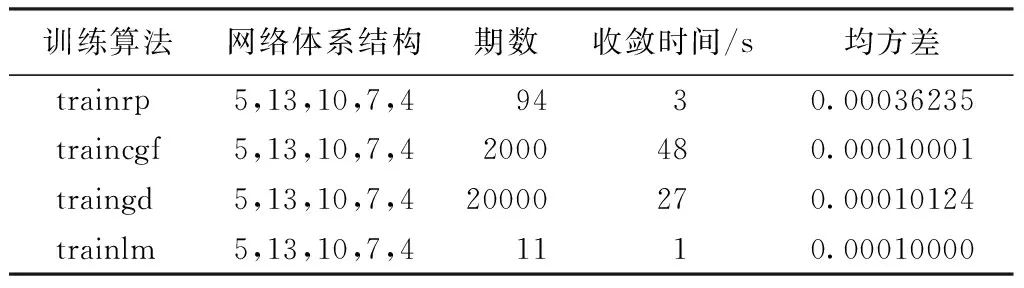
表2 整体钻头对沉积岩不同训练算法的性能Table 2 Performance of the integrated drill bit for different training algorithms of sedimentary rocks
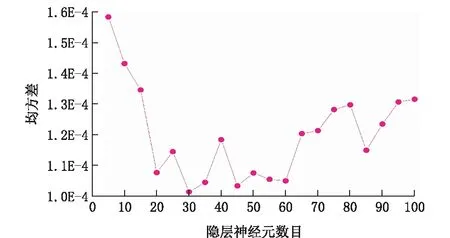
图6 L-M算法隐含层中神经元数目与MSE值Fig.6 Number of neurons and MSE values in the hidden layer of L-M algorithm
3.3 基于神经网络的岩石特性预测
将自变量代入到人工神经网络模型中,得到单轴抗压强度σc、施密特回弹数SPN、岩石干密度ρ及抗拉强度στ的估计值,将估计值与实际值在一个图上表示出来,见图7~10,图中将实际值连成一条直线,这样可以很明显的看出预测值与实际值的偏差(以横坐标所示数值为参考)。
3.4 模型预测性能
为了检验一个预测模型的表现情况,通常需要计算出相关的指标参数。其中,决定相关系数(VAF)和均方根误差(RMSE)就可以准确反映出所建立的预测模型的性能是否优良。
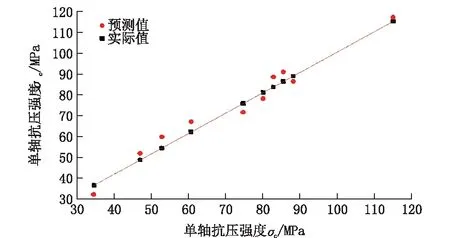
图7 σc预测值与实际值Fig.7 Predicted and actual values of uniaxial compressive strength
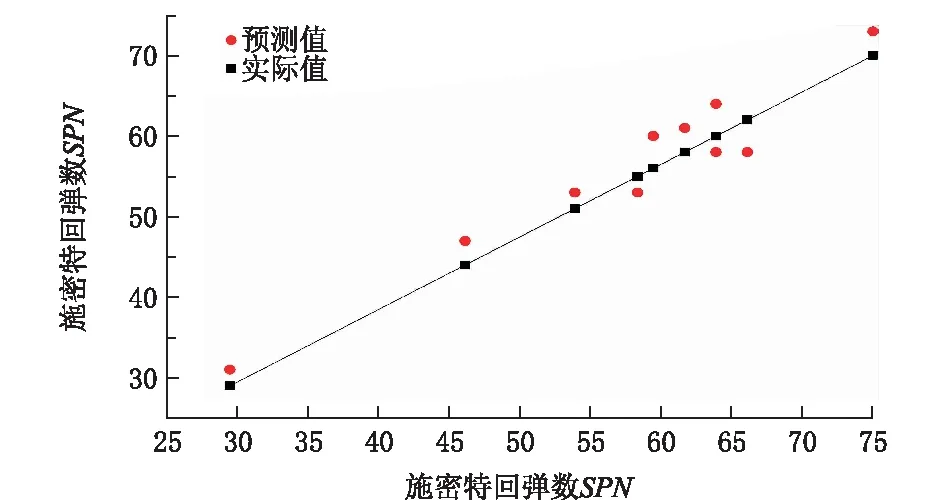
图8 SPN预测值与实际值Fig.8 SPN predicted and actual values
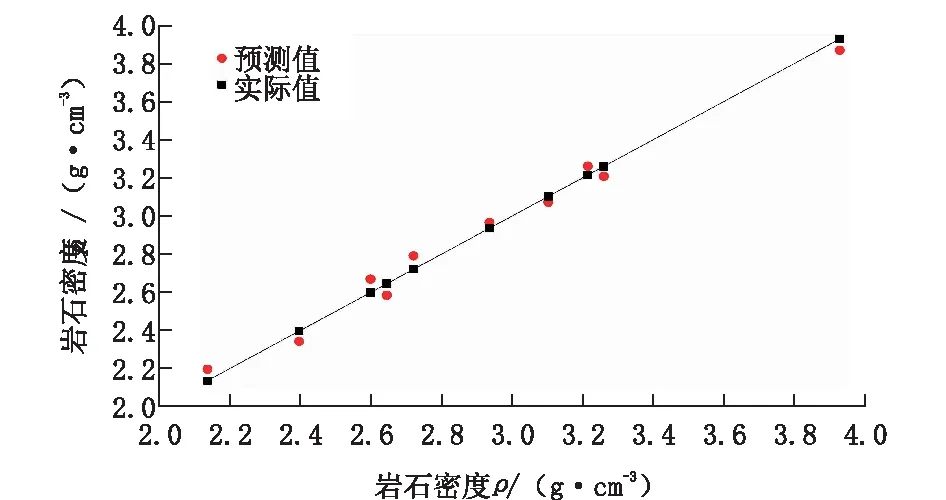
图9 岩石密度预测值与实际值Fig.9 Predicted value and actual value of rock density
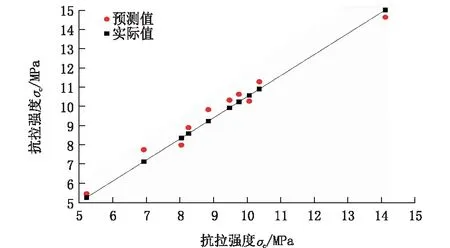
图10 抗拉强度预测值与实际值Fig.10 Predicted and actual values of tensile strength
(2)
(3)
式中:yi——测量值;yi′——预测值。
一般来说,评价一个预测模型的性能主要看其VAF和RMSE的值,如果VAF最大且RNSE最小,则表明这个模型性能是稳定且优良的。同时,对于模型预测的准确度也可以通过平均绝对百分比误差(MAPE)来计算,即:
(4)
式中:Ai——实际值;Pi——预测值。
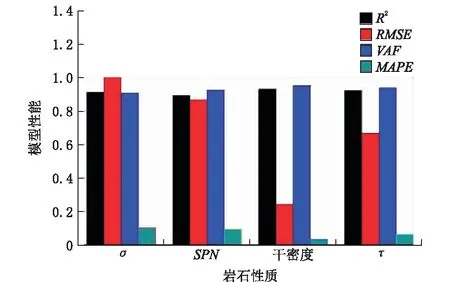
图11 回归模型的性能指标Fig.11 Performance indicators of the regression model
图11列出了建立的回归模型的性能指标。可以观察到,所开发的预测岩石性质模型对岩石密度更有效,因为它具有低的RMSE和高的VAF值。这些值可用于将已开发模型的性能与其他间接调查进行比较。对于单轴抗压强度σc、岩石密度ρ、施密特回弹数、抗拉强度στ,MAPE值分别为10.4578、9.1264、3.2529、6.096,对应的预测准确率为89.54%、90.87%、96.75%和93.9%,这间接地解释了预测模型的可靠性。
4 结论
本论文在考虑钻头直径、钻头转速和钻进速率的影响下,对钻进过程中岩石与钻头接触所产生的等效声级进行了研究分析,得出以下结论:
(1)在岩石钻进过程中,产生的等效声级与表征岩石特性的物理参数表现出了良好的相关性。其中等效声级与单轴抗压强度σc、岩石密度ρ、抗拉强度στ间呈指数函数关系,而与岩石施密特回弹数呈线性函数关系。
(2)利用人工神经网络建立了预测岩石性质的模型,通过对模型的训练和测试,找到了可靠的模型,并进行了基于等效声级的岩石性质预测,预测模型计算出的岩石特性值和实际值比较接近
(3)通过对预测模型的性能分析,对岩石单轴抗压强度σc、密度ρ、施密特回弹数、抗拉强度στ,预测准确率分别为89.54%、90.87%、96.75%和93.9%,表明了模型的有效性。

