《算海说详》中珠算开方新增法及其特点——兼与《算法统宗》开方法的比较

牛 腾

(中国财政科学研究院，北京 100142)

开方法是中国古代重要且复杂的算法，古人最初使用算筹进行开方，后来发展为用算盘作为主要开方用具。元明时代基本完成了从筹算开方到珠算开方的过渡，此后珠算开方法逐渐发展完善，这主要体现在《算法统宗》(以下简称《统宗》)这一珠算著作中。在此之后的很多珠算著作大多以《统宗》为底本完成，如清代李长茂(1)李长茂，字拙翁，号睡足轩强恕居士，山东章丘县人。据高峰和冯立昇[1]考证，李长茂于顺治十六年(1659)，开始编纂算书，是年四月，写成《算海说详》九卷，顺治十八年(1661)付梓刊行。康熙元年(1662)李长茂对原书加以挖补修改，请沈世奕作序，再次印行。现存两种版本分别为1661年萧维枢作序的初刻本，和1662年沈世奕作序的修补本。所著《算海说详》(以下简称《说详》)就是其中一部比较典型的珠算著作。华印椿([2]，页86—88)、劳汉生[3]等认为，《说详》是以程大位的《算法统宗》(以下简称《统宗》)为蓝本，删繁就简，压缩而成。李培业[4]称，《说详》第一卷为汇法章，介绍各种珠算法，多系《统宗》内容，但所论甚详；以下各章，多为“九章”内容。《世界珠算通典》[5]、《中华珠算大辞典》[6]等称，《说详》内容仍不出《统宗》范围，而所论较详。前述说法并不完全符合事实，该书确实以《统宗》为蓝本编纂而成，但不止“删繁就简”，还增加了不少新内容，如对原有内容的解释说明，以及新增加了一些歌诀、算法等。

以《说详》开方法为例，该书突破了以往算书“九章”的编排，其“算法九章名义”称：“开方章，万法不离方，求诸算多用开方，故次勾股”([7]，页565)，认为开方法是比较基础且重要的运算方法，故单列一章专讲开方，即第四卷开方章，对应《统宗》卷六少广章。在《统宗》基础上，《说详》对开方问题进行了新的编排，除了包含《统宗》已载解法，还删减了一些例题，并新增了与之不同的解法。且每例解后，《说详》还设有“解义”，对解法算理、解题过程或几何含义等进行详细阐释，《统宗》则没有此类说明。最重要的是，明代以前的珠算开方法基本都是借助开方作法本源中的常数进行运算，而《说详》新增的大部分开方法已没有这一特征。因此，《说详》开方法能很好地展示珠算开方的发展历程，对其开方法的研究对数学史和珠算史都具有重要意义。

现有研究中，对《说详》中珠算开方问题的关注少之又少，华印椿([2]，页385—388，449—451)等进行过简要介绍，高峰[8]对《说详》进行了校注，但鲜有人对《说详》所载珠算开方法进行过系统研究。本文以《说详》1661年初刻本为底本，以《说详》开方新增法为中心，通过与《统宗》中开方法的对比，从算盘的具体操作及开方的代数和几何含义着手，重点研究《说详》新增珠算开平方、开立方和开三乘方法的特点和创造性。鉴于珠算开方法有商除开方和归除开方两类，《说详》所载归除开方法与《统宗》基本相同，所以本文只分析两算书中珠算商除开方法之异同，并以此分析珠算商除开方的发展历程。

1 珠算开平方法的特点分析

1.1 《算法统宗》珠算开平方法

《统宗》首先介绍了“开平方法认商歌”和“开平方初商定首位诀”，然后对开平方法有一般性解释：“法曰：置积为实，别置一算名曰下法，于实数之下自末位至首常超一位，约实一下定一，千百下定十，万下定百，百万下定千，实上商置第一位得若干，下位亦置上商若干，名曰方法……”([9]，页1308)，其中仍使用“别置一算”“实数之下”“实上”等用语，且在实数之下借一算用以定商位，“借算”有进位变化，可见布算上是将各项从上至下排列，很大可能属于筹算开方法。但传统筹算开方法中又有“借算”的退位变化，或方廉隅的进位或退位等变化，此方法中却没有，应当是一种简化后的新的筹算开平方法[10]。之后《统宗》先载有“开方求廉率作法本源图”(2)《统宗》将“开方求廉率作法本源图”置于开平方法的介绍之中，《说详》也载有此图，称为“开方求廉率旧图”([7]，页628)，并将之置于对开方章的总体介绍之中。可见，《说详》此处的调整更为合理。([9]，页1309)，随后列举六例具体展示其珠算开平方法。其珠算商除开平方基本继承自已有筹算开平方法，以“今有方田积七万一千八百二十四步，问平方一面若干”为例，用算盘展示其开平方运算过程(表1)；用字母a，b，c分别代表初商、次商、三商(3)下文中的a，b，c均指代此含义，且文中a，b，c均不指代例解中的具体数字。，并用代数语言说明相应的运算程序(表2)。

①原文似因排版问题,最后部分皆为小字,今按其行文习惯改之。

图1 贾宪“开方作法本源”

表2 程大位商除开平方法运算程序

序号商实方法(廉法)隅法1aN-a2=N1a2a+bN1-(2a+b)b=N22ab3a+b+cN2-(2a+2b+c)c2a+2bc

根据表1和表2，其开平方法布算分商、实、方法(廉法)、隅法四项，按从左至右顺序排列；使用了方法、廉法、隅法等术语；初商根据口诀求出，没明确说明次商(或三商)如何求得，根据其算理，应该是以2a(或2a+2b)为法数求出。其珠算开平方法对应的代数式为：

(a+b+c)2=a2+(2a+b)b+(2a+2b+c)c

其中所使用系数2，实际是取自“开方求廉率作法本源图”之平方率，最早可追溯至贾宪“开方作法本源”([11]，页1416)(图1)，即贾宪三角。在此之前的开平方法基本都采用此类方法，即借助开方作法本源中“平方”的常数进行运算。

结合术文作图2展示《统宗》商除开平方法的几何含义，其中图2-(1)与《统宗》所载“一方四廉两隅演段图”基本相同。在此之前的商除开平方法也基本能用图2展示其几何含义，只是中间减去各项的顺序不尽相同。

图2 分解正方形展示《统宗》商除开平方法的几何含义

1.2 《算海说详》珠算开平方新增法

《说详》在介绍具体开平方法之前，载有“开方算盘定位之图”云：“左商位；积实居中，自左而右；右法位”([7]，页629)，其后解释中虽有“积实之下”的说明，但其实明确了在算盘中将商置于左，实置于中，法置于右。且没有使用“借算”，没有明显筹算开方布算之特点。在这之后，《说详》选取了《统宗》商除开平方例题中的两例进行介绍，例解中“旧法”与《统宗》所载基本相同，除此外，还新增了“商除本位开方法”，有歌诀如下：

商除本位开方法歌

商位开方法尤精，不用双廉一隅称。初商自呼除方积，次商呼初除积行。又用次商呼初次，除完廉隅皆在中。三商四商同一理，惟此省便易为功。([7]，页630)

歌诀中明确此法不用“双廉一隅”用语，且基本说明了其运算程序。其后有一例与前引《统宗》开平方例题相同(此处略)，但解法不同。根据原术文，用算盘展示其开平方运算过程，并用代数式表示出相应的运算程序(表3)。

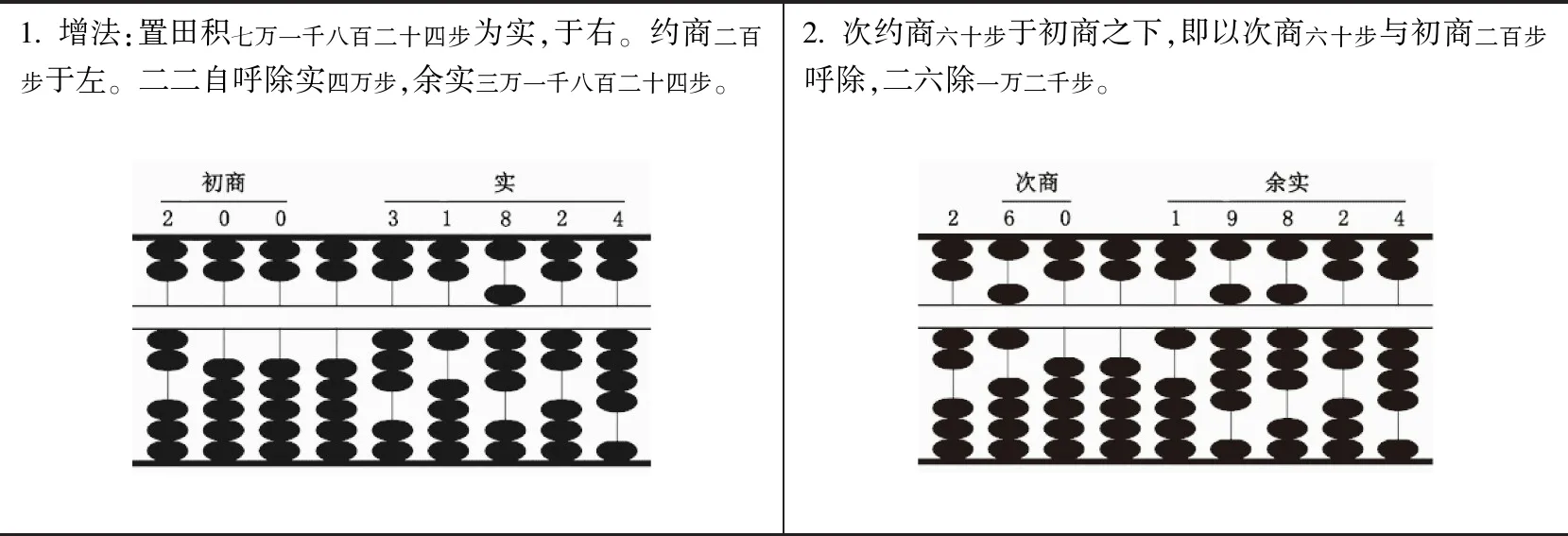
表3 用算盘和代数式展示《算海说详》“商除本位开方法”

续表3

根据表3，《说详》开平方新增法布算分商、实两项，盘面比较简洁；其术文与歌诀相对应，没有使用廉法和隅法两用语，也没有使用方法等用语，叙述比较简洁；初商根据口诀求得；没明确说明次商(或三商)如何求出，根据其算理，或许是以a(或a+b)为法数求出。且此法与之前的开平方法在运算程序上均有很大不同，乘减过程中需多次减去商数与相关项的乘积，对应的代数式为：

(a+b+c)2=a2+ab+(a+b)b+(a+b)c+(a+b+c)c

运算过程中没有商数加倍，或在原数基础上再加商数的步骤，不再借助开方作法本源中“平方”的常数进行运算，在此之前未曾见过《说详》新增珠算开平方法，也未见有类似的筹算开平方法。而且也不能以图2解释其开平方法的几何含义，今另作图3说明其几何含义。

图3 分解正方形展示李长茂“商除本位开方法”的几何含义

2 珠算开立方法的特点分析

2.1 《算法统宗》珠算开立方法

《统宗》共介绍了两种珠算开立方法，介绍开立方法一之前首先载有“开立方法歌”：

自乘再乘除实积，三因初商方另列。次商遍乘名为廉，方法乘廉除次积。次商自再乘名隅，依数除积方了毕。初次三因又为方，三商徧乘仿此的。([9]，页1321)

从歌诀判断布算有商、实、方、廉、隅五项，其后“解曰”对口诀进行了解释和说明。书中同样著有开立方初商口诀，还有对开立方法的一般说明：“法曰：置积为实，别置一算名曰下法，于实数之下自末位至首常超二位，约实千至九十余万俱定十。百万后俱定百。实上商置第一位得若干……”([9]，页1322)，仍是从上至下排列各项，有“借算”，且“借算”有进位变化，没有方廉等的进位或退位变化，可能也是一种新的筹算开立方法。其后共有四则例题，以“今有积一百九十五万三千一百二十五尺，问立方面若干”为例，用代数语言展示其珠算开立方运算程序(表4)(4)其算盘运算图详见文献[12]。。

表4 程大位商除开立方法一之运算程序

根据表4，《统宗》开立方法一实际布算为商、实、下法、方法、廉法、隅法六项，这点与“歌诀”所示略有不同；初商根据口诀而得，没有明确说明次商(或三商)如何求出，据其算理推测，次商很可能是用3a与余实相商而得(见步骤2)，而三商很大可能是用3(a+b)与余实相商而得(见步骤4)；运算时，先在余实中减去方法与廉法的乘积，然后求隅法的值，再从余实中减去隅法。

上述运算对应的代数式是：

(a+b+c)3=a3+3a(a+b)b+b3+3(a+b)(a+b+c)c+c3

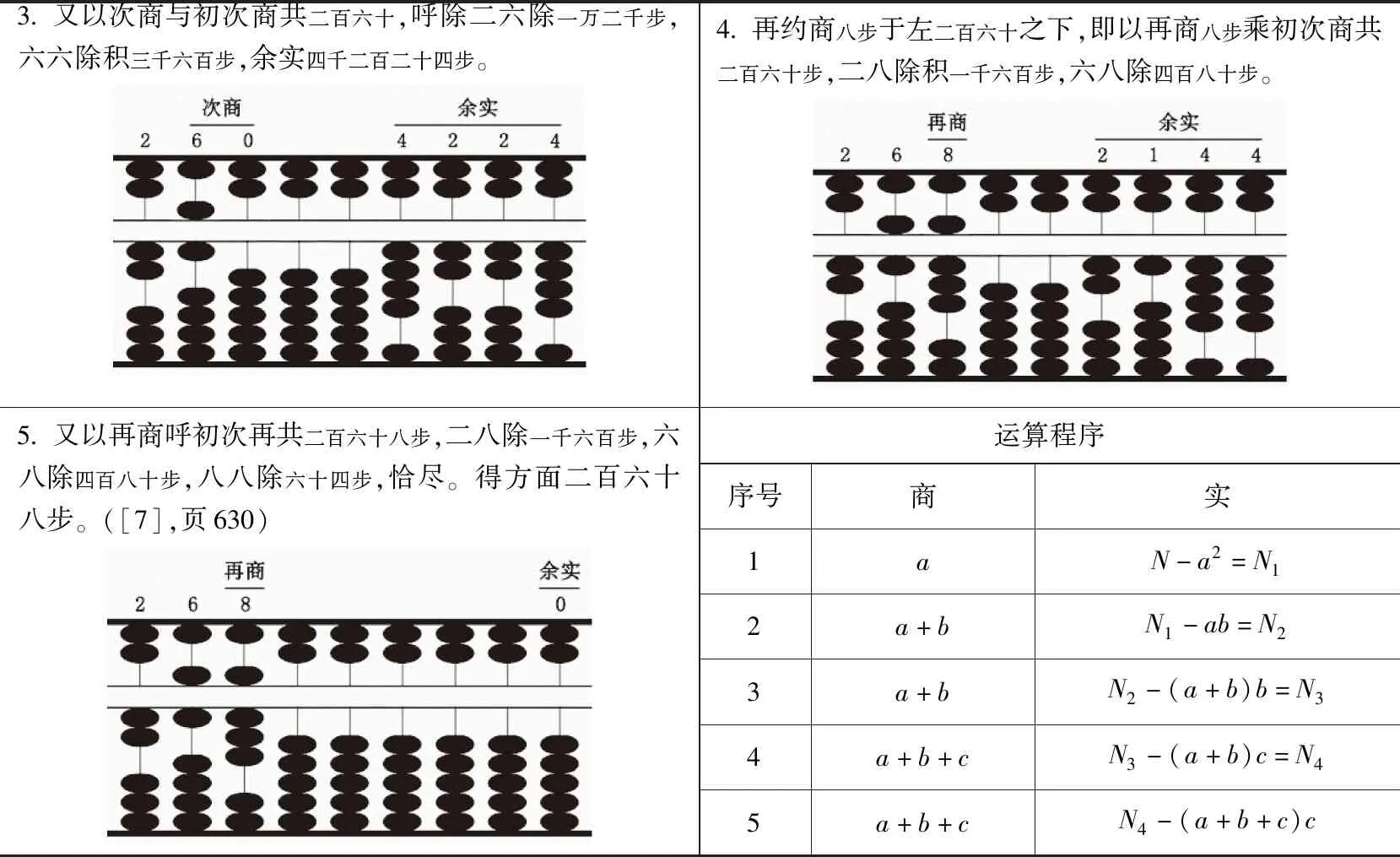
借助开方作法本源中“立方”的常数3，3进行运算。作图4展示《统宗》开立方法一的几何含义。

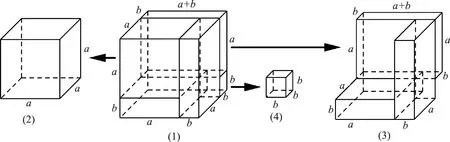
图4 《统宗》珠算商除开立方法一对应的几何图(5)因《统宗》开立方法一对应的几何图形较复杂，这里仅展示其中求初商a和次商b时对应的几何图。

除此之外，《统宗》在“开立方带纵法”一条最后一题(该例题的立方积是3375尺，方面为15尺)的例解中，介绍了与之不同的开立方法(法二)：

法曰：置积三千三百七十五尺为实，以开立方法除之。古法用三为廉率。约实定位，从实末位尺，十尺定尺，百尺、千尺定十尺。初商一十于左，下法亦置初商一十，自乘得一百，再乘得一千，除实讫。余实二千三百七十五尺。却以下法初商一十自乘得一百，用三因为方法。又以初商一十，以三因得三十为廉。次商五尺于左初商之次，下法亦置次商五尺，自乘得二十五尺为隅法。又以次商五尺乘廉三十得一百五十为廉法。并方法三百，廉法一百五十，隅法二十五，共四百七十五尺。皆与次商五尺相呼，四五除二，五七除三十五，五五除二十五，恰尽。得方面一十五尺。合问。([9]，页1327)

《统宗》称之为“古法”，又用珠算完成，或许在这之前就已有这种珠算商除开立方法。其布算仍为商、实、下法、方法、廉法、隅法六段，但方、廉、隅法的含义与珠算开立方法一中的不同；初商根据口诀求出，没有说明次商如何求出，根据其算理，应该是以3a2+3a为法数与余实相商而得，此运算对应的代数式为：

(a+b)3=a3+(3a2+3ab+b2)b

仍是借助开方作法本源中“立方”的常数3，3进行运算。作图5展示《统宗》开立方法二的几何含义。

综上，《统宗》珠算商除开立方法一相比法二似乎是新法，但法一估商所用的法数比法二估商所用的法数要小，这会影响估商的正确性。而且两方法中廉隅等术语的含义、运算程序及对应的代数、几何含义各不相同。但它们的共同之处是，都是借助开方作法本源中“立方”的常数进行运算，且在此之前都能找到相似的筹算开方法。

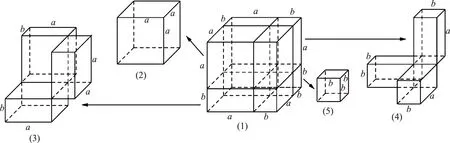
图5 《统宗》珠算商除开立方法二对应的几何图

2.2 《算海说详》珠算开立方新增法

《说详》也载有“开立方法歌”云：

立方之法要推详，自乘再乘始初商。三因自乘面方法，三因初商三廉长。次商又乘全廉阔，次商自乘隅法当。合并三法次商乘，积余再商依次商。([7]，页635)

明显与《统宗》中“开立方法歌”不同，但与其开立方法二相对应。其后“立方商法一方三平廉长廉一隅图”、例题并解法也与《统宗》开立方法二之图示、例解等基本相同。《说详》载第二种方法为“又立方问面法”，无歌诀，解法与《统宗》开立方法一基本相同。即《说详》继承了《统宗》的两种珠算商除开立方法，并称它们为“旧法”，但对两算法的顺序进行了重新整理。

除此之外，《说详》新增了一种开立方法，并载有“开立方捷法歌”：

捷法可求开立方，不用廉隅费思量。初商再乘除方积，就约余积定次商。合并初次自乘讫，又用初乘初次商。再置初商亦自乘，三数总合次乘良。得数除积知方面，三商四商依样详。([7]，页636)

其后例题与前引《统宗》“今有积一百九十五万三千一百二十五尺”相同，但解法不同，用算盘展示其开立方运算过程(表5)，并用代数语言表示出相应的运算程序(表6)。

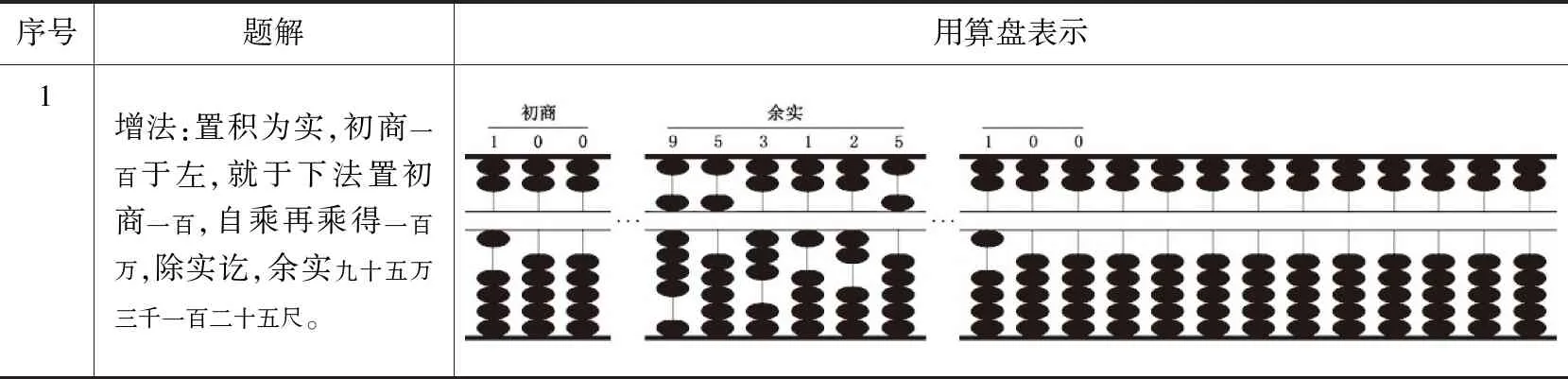
表5 用算盘展示李长茂开立方捷法

续表5

①原文作“一”,今据算理校改为“二”。
②原文作“次”,今校改为“数”。

表6 《说详》开立方新增法运算程序

据表5和表6，《说详》开立方新增法布算最多有五段；没有使用方廉隅等术语；初商根据口诀求得；没有说明次商和三商如何得出；每次乘减完成后，下一步都重新计算需要乘减的数。华印椿说其布算只有商、实、下法三段([2]，页468)，但其实只用到了商、实、下法三个名称，除了商、实两项以外，实数右侧参与运算的各项均称作“下法”，包含三段。旧法与增法各有千秋，但李长茂自认为他的新法克服了旧法的缺点，可以少“费思量”，故自称捷法。但他没有说明次商和三商如何求得，这使得其开立方增法并不容易掌握和理解。

另外，上述运算对应的代数式是：

(a+b+c)3=a3+[(a+b)2+(a+b)a+a2]b

+[(a+b+c)2+(a+b+c)(a+b)+(a+b)2]c

可见《说详》开立方新增法并未借助开方作法本源中的常数进行运算，且在此之前未见有类似的珠算开立方法及筹算开立方法，也不能以图4和图5说明其几何含义，另作其开立方新增法对应的立体几何图(图6)。

图6 《说详》开立方新增法对应的几何图(6)因《说评》开立方法新增法对应的几何图形较复杂，这里仅展示其中求初商a和次商b时对应的几何图。

3 珠算开三乘方法的特点分析

3.1 《算法统宗》珠算开三乘方法

《统宗》没有关于开三乘及以上方的条目或专门的记载，或许是因为这种算法不常用，也或许是因为珠算开三乘方法比较困难，还没有过专门的说明。该书“开立方带纵法”一条第四题“今有(二)[三]乘方积二千零一十五万一千一百二十一尺，问一面若干”为唯一一则开三乘方例题，以之为例，用算盘展示其开三乘方法(表7)，并用代数语言说明其运算过程(表8)。

表7 用算盘展示《统宗》开三乘方法

表8 用代数语言说明《统宗》开三乘方法运算过程

据表7和表8，《统宗》开三乘方法布算分商、实、方法、上廉、下廉和隅法六项，术文中“下法常超三位”仍然采用筹算开方的习惯性说明，根据字面意思，指的是下法从实数最末一位往前超三位，也就是前进四位约实数。即步骤1中的“下法”是指借算，有进位变化，但此后再无借算的其他说明。后续步骤中的“下法”是指方廉隅等项，没有关于位置的说明，因是珠算开方，可能放置于算盘之右侧；但又因项数较多，也可能另置算盘进行运算。文中没有说明初商或次商如何求得，根据其算理，次商或许是以4a3+6a2+4a作为法数与余实相商估算而得。该解法对应的代数式为：

(a+b)4=a4+(4a3+6a2b+4ab2+b3)b

借助开方作法本源中三乘方的常数4，6，4进行运算。

其实此法与周述学《神道大编历宗算会》(以下简称《历宗算会》)(1558)的一例解相似，其文曰“置积为实，别置一算名曰下法，从实尾数至首，常超三位，于万下定一十。置初商一十于左上……”[13]，运算过程中没有下法、方廉隅等的退位变化，并将初商放置在左上，很大可能是珠算开三乘方法。说明在此之前已有类似解法，且《历宗算会》和《统宗》中的珠算开三乘带从法也很相似[14]，可见两书有不小的渊源。

此外，程大位还介绍了开三乘方的第二种方法：

一法用二次开平方法除之亦得。初一次，置积数为实，以开平方法除之，商得四千四百八十九尺。第二次，就以此初商数为实，亦以开平方法除之，即得一面六十七尺，合问。此又捷径。([9，页1327])

也就是用两次开平方法求得，而朱载堉求12次方是经过两次开平方、一次开立方求得，开24次方是通过三次开平方，一次开立方求得。这说明对于开高次方来说，不论是筹算还是珠算，人们采用将高次方法化成低次方法是比较普遍的做法。

3.2 《算海说详》珠算开三乘方新增法

与《统宗》不同的是，《说详》单列“开三乘立方法”一条介绍珠算开三乘方法，但只有例题并解法，例题与前引《统宗》“今有三乘方积二千零一十五万一千一百二十一尺”同，“旧法”与前引《统宗》第二种方法相同，“又法”与前引第一种方法相似。但“又法”中，《说详》没有“下法常超三位”的说明，称“置积为实于中，初商六十于左，下法亦置六十于右……”([7]，页638)，明确说明各项从左至右排列，却又没有说明开三乘方之定商方法。

除了对《统宗》珠算开三乘方法的继承，《说详》中还给出了两种不同于上述解法的珠算开三乘方法，分别称为“增法”和“又增法”。首先用算盘展示《说详》开三乘方“增法”(表9)，并用代数式展示其运算过程(表10)。

表9 用算盘展示李长茂开三乘方法“增法”

表10 《说详》开三乘方“增法”的运算程序

据表9和表10，此开三乘方法布算分商、实、法三项，但法数一项最多时包含4段数字；没有“下法常超三位”等筹算痕迹；除了使用“小立方”“平廉”“长廉”“隅法”等用语外，还使用了“小方平廉”“小方长廉”“小方隅法”“平廉立阔”“长廉横阔”“长廉立阔”等用语；没有说明初、次商如何求得，误差很大。根据其原术文可知，该解法是以分解几何图形来说明开4次方的运算方法，中间步骤中的(a+b)3是相当于开立方，所以文中多次用到小立方，以及开立方中用到的各种术语，如平廉、长廉、隅法等。

该解法对应的代数式如下：

(a+b)4=(a+b)(a+b)3=a(a+b)3+b(a+b)3
=a(a3+3a2b+3ab2+b3)+b(a+b)3
=a4+(3a2b+3ab2+b3)a+(a+b)3b

也就是不用开方作法本源中三乘方的常数4，6，4进行开三乘方运算，而是借助于开方作法本源中“立方”各项常数3，3进行运算。

除此之外，《说详》还新增了另一种开三乘方法，用代数语言解释其运算过程(表11)。

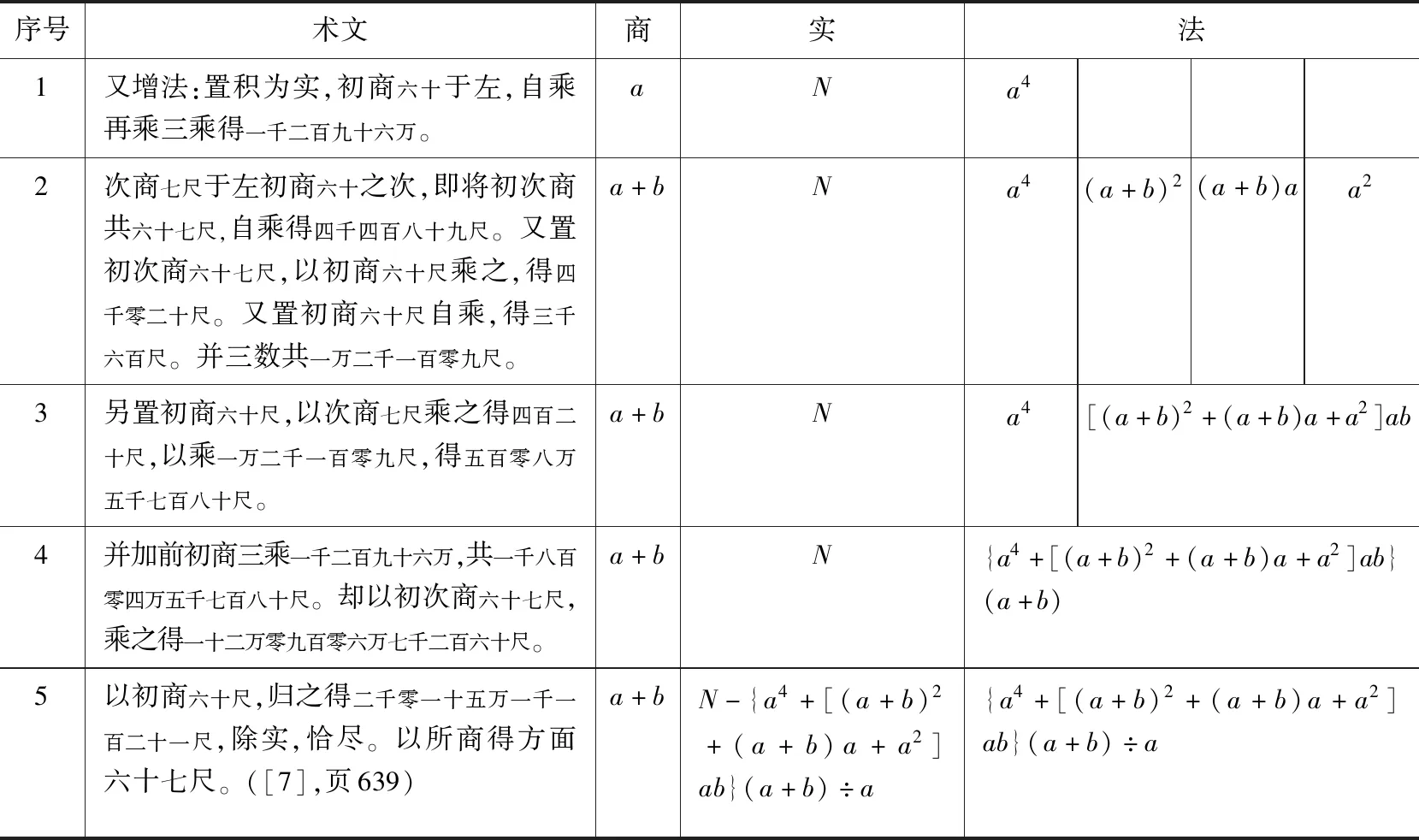
表11 《说详》开三乘方“又增法”的运算过程

据表11，布算仍分商、实、法三项，但法数一项最多时也包含4段数字；没有“下法常超三位”等筹算痕迹，但也没有说明初商位的定商方法；运算过程中不使用廉隅等用语，文字较前一种方法更简洁；没有说明初、次商如何求得。

该解法对应的代数式如下：

其中

图7 《历宗算会》“开三乘方图[13]”

对应的是李长茂不用廉隅开立方法的代数式。不借助开方作法本源中的常数进行运算。在此之前，未见有类似的筹算开三乘方法和珠算开三乘方法。

求次商及其后各商是开方法特别是开高次方中的重中之重，李长茂新增的两则开三乘方法均没有说明次商如何求得，而且运算过程并不简捷，特别是第2种方法需要计算多个乘数是两位数的乘法运算，还需要进行归法(即除法)运算，增加了运算难度。

开平方可以用分割正方形的方法表示之，开立方可以用分割正方体的体积表示之，中国古代有些算学家也对四次方图形进行了描述，如杨辉《详解九章算法》中称“三度相乘，其状匾直”([11]，页1426)，然现存书中没有此图。周述学《历宗算会》给出了开三乘方立体图形(图7)进行说明。《说详》则称“三乘者，立方之上再加高，如窖深之类是也”，但都不能反映其真实情况。《统宗》介绍“三乘方”称“其形不知如何模样，只是取数而已。”([9]，页1309)其实在三维空间中，三乘方形不可能用类似图7中的几何体来表示，而开三乘方在现实生活中也难以找到直观的原型[15]。清初梅文鼎就曾指出前人在乘方方面的错误认识，并说：“三乘方以上不可为图，诸书有强为之图者，非也。[16]”可见中国古代有些算学家对此缺乏正确的认识。

4 《算法统宗》与《算海说详》珠算开方法的比较分析

为便于分析，将《统宗》珠算商除开方法分别与《说详》新增法的特点进行对比研究(表12)。

表12 《统宗》开方法与《说详》开方新增法的特点分析

根据表12，我们得出：(1)《统宗》珠算商除开平方法与《说详》新增相比，有以下共同点：皆为横式排列；必有商、实两项；初商依据口诀求出；没有说明次商和三商如何求得。不同之处在于，《统宗》开平方法使用四段数字布算，《说详》则使用两段数字进行运算；《统宗》开平方法使用方廉隅等用语，《说详》新增法未使用此类用语；《统宗》开平方法借助开方作法本源中平方之常数进行运算，《说详》新增法则没有。(2)《统宗》珠算商除开立方法与《说详》新增法相比，有以下共同点：皆为横式排列，必有商、实、下法三项，初商依据口诀求得，没有说明次商和三商如何求得。不同之处在于，《统宗》两种开立方法使用六段数字布算，《说详》则使用五段数字进行运算；《统宗》两种开立方法皆使用方廉隅等用语，而《说详》新增法并未使用此类用语；《统宗》两方法皆借助开方作法本源中立方各项常数进行运算，《说详》则没有。(3)《统宗》珠算商除开三乘方法与《说详》新增法相比，有以下共同点：必有商、实、法三项，且最多有六段数字；没有说明初、次商如何求得。不同之处在于，《统宗》开三乘方法布算时有借算，且借算有进位、无退位变化，《说详》新增两种方法布算时都没有借算一项；《统宗》开三乘方法使用方廉隅等用语，《说详》“又增法”未使用此类用语；《统宗》开三乘方法借助开方作法本源中三乘方各项常数进行运算，《说详》“增法”借助开方作法本源中立方各项常数进行运算，其“又增法”则未借助开方作法本源中常数进行运算。

结合前文分析，我们还发现，《统宗》除载有珠算开方法外，还载有筹算开方新法，体现了筹算开方到珠算开方的过渡状态，《说详》则基本没有筹算开方布算之特征。《说详》新增法与《统宗》珠算开方法相比，其代数和几何含义都与之不同，在《统宗》珠算开方法之前，都能找到与之相似的筹算开方法，但在《说详》之前，未见与其珠算开方增法相似的筹算开方法。《说详》中有些新增开方法，在布算和叙述上比《统宗》开方法简洁，当是在《统宗》珠算商除开方法的基础上，为简化运算过程而对整个运算程序进行的改进。但从代数含义以及该方法的操作性来分析，《说详》有些新增法并不比《统宗》的便捷。

此外，从珠算开三乘方的发展可以看出，由于其复杂性，由筹算商除开高次方法到珠算商除开高次方法的过渡不如珠算开平方、开立方等容易。如《统宗》对开三乘方的运算说明虽然明确各项从左至右排列，但是仍借用一算并以“下法常超三位”的方式定商数的位数。《说详》则没有说明开三乘方之定商方法，后来，梅瑴成在《增删算法统宗》中对“下法常超三位”有“即合四位为一段，乃定位之法”[17]的注解，才比较清楚的说明了珠算开三乘方定初商之法。可见，珠算开三乘方法的发展更加缓慢。

5 结语

一般认为，珠算开方由筹算开方发展而来，后又完成了从珠算商除开方法到珠算归除开方法的过渡，这从《统宗》中能得到很好的印证。明代以前的珠算商除开方法基本都能找到与之对应或相似的筹算开方法，且无论开方法如何发展，其共同点都是借助开方作法本源中的常数进行运算。但在以《统宗》为底本写成的《说详》一书中，却新增了一些珠算商除开方法，它们在运算程序上发生了很大变化，且在这之前无法找到与之对应或相似的筹算开方法。

通过对《统宗》与《说详》中商除开方法的分析，我们发现，《说详》在继承《统宗》原有珠算开方法的基础上，删除了一些内容，保留了具有代表性的例题，对开方章中的内容进行了新的总结、分类和研究，对其中一些开方内容还进行了重新编排，比《统宗》更有条理性。且《说详》开方法已基本没有筹算开方的特征。《说详》新增开方法与《统宗》原有方法相比，前者有些方法在布算和叙述上更加简洁，如《说详》开平、立方增法的布算项数都比《统宗》少，所置数字更少，因此盘面看起来更简洁；除了开三乘方“增法”，其他开方增法都不再使用方廉隅等用语。且其新增法在运算方法上有大的改革和创新，即《说详》创造了不借助开方作法本源中常数的开平方、开立方、开三乘方法，以及借助开方作法本源中立方之常数的开三乘方法。这些发明反映了开方法从借助开方作法本源中常数到不借助开方作法本源中常数进行运算的发展过程。

但需要说明的是，《说详》新增开方法并非都是简便的，没有运算歌诀或通用的解法说明，从其运算程序来看，不如借助开方作法本源中常数进行运算时有规律可循。其中很多方法没有说明如何求得次商及以后各商。且依据其算理可以发现，有些方法在求次商或三商之时借助的法数太小，存在估商困难、容易造成很大误差及影响运算效率等缺点。另外，《说详》对开方法的论述还有一大特点，即几乎都是用分解几何图形的方式阐释其运算过程或算理，但对于开三乘方法来说，现实生活中并不存在他所描述的几何图形。

致 谢本文为笔者博士论文的一部分，承蒙导师邹大海研究员的精心指导，谨此致谢！同时感谢审稿专家和编辑部老师提出的宝贵意见！