节地减损开采模式下边坡结构及应力发展规律

尚 涛，韩 流，舒继森，陈树召

(中国矿业大学 矿业工程学院,江苏 徐州 221116)

煤炭作为我国的主要能源，其开采量和消费量均居能源结构的首位[1]。“十二五”以来，我国原煤产量一直维持在35亿t/a以上，且在未来相当长的一段时期内不会发生根本性改变。露天开采具有建设速度快、生产成本低、资源采出率高、安全性好等优势，近年来取得了快速发展[2]。自21世纪初至今，露天开采的煤炭年产量由0.6亿t/a提高到了6.6亿t/a，占我国煤炭年产总量的比重由5%提高到了17%。我国大型露天煤矿主要分布在内蒙、新疆、云南等偏远地区，大规模的剥离和采矿作业造成了地层结构和生态植被的大规模破坏[3]，给内蒙、新疆等生态脆弱地区的环境带来了严重的影响[4]。

内蒙古东部草原区位于我国生态安全“两屏三带”的北方防沙带，具有酷寒、半干旱、土壤瘠薄等生态脆弱特征。近10 a来，露天煤矿的大规模建设和煤炭资源开发造成了地表植被破坏、加剧了矿区沙漠化和水土流失进程，加速了当地生态系统的退化。针对露天开采需要大规模剥离-排弃的作业特点，基于时效边坡理论研发露天矿节地减损开采技术来压缩对土地的挖损或压占，降低对矿区生态的影响具有良好的社会和环境效益。

节地减损开采的核心技术在于提高端帮边坡角度[5]，以煤炭资源的边界为基准，端帮每提高1°则意味着矿区地表境界以煤炭边界为圆心向采场内收缩1°。按照采深200 m、端帮地表长度1 km计算，端帮提高1°，可节约土地7 000 m2，具有显著的研究价值和应用前景。对于缓解资源开发造成的矿区生态退化问题具有十分重要的现实意义。

节地减损技术是在传统的靠帮开采基础上衍生出来的一种综合安全和环境效益的绿色开采技术。目前，关于靠帮开采和时效边坡的相关研究较为丰富，2006年，才庆祥等[6]根据分区开采露天矿采场的动态发展特征，充分利用端帮边坡的服务周期和岩体的时效性，提出了时效边坡理论和靠帮开采技术[7]，并在安家岭、黑岱沟、哈尔乌素等大型露天矿进行了成功应用。刘勇等[8]根据露天矿推进度、边坡角度、高度等参数，建立了端帮边坡暴露时间模型。韩流等[9]对采矿工程的作业程序进行调整，采用内排及时跟进压帮的方式，实现了对端帮易滑区下部的资源的安全回收;同时根据软、硬岩的破坏特征，建立了直线和曲折滑面渐进贯通过程中的时效稳定性分析方法[10-11];最后采用理论分析和数值模拟研究了边坡几何结构差异对稳定性的影响，证明了凹形边坡的稳定性优于相同角度的平直、凸型边坡，并揭示了凹形曲率与坡高之比对边坡稳定性的影响规律[12]。

在软岩地质条件下进行爆破[13]、开挖、堆载工程作业，会对区域应力结构造成较大的扰动。露天开采及排土堆载会对地层结构及应力状态产生较大的影响，尤其在高应力地区表现的更加明显。由于软岩具有弹、塑性及流变特性[14]，开挖-排土过程中边坡结构变化造成的不平衡地应力卸荷会导致周围区域岩体变形，甚至诱发边坡失稳。林刚等[15]借助数值模拟手段研究了不平衡堆载作用下深基坑开挖支护结构形状，揭示了基坑两侧围护结构内力、位移存在的差异，并总结出了有参考价值的基本规律。唐燕蕾和杨石飞[16]研究了大面积堆载对土地水平位移的影响规律，分析了不同影响因素对水平位移和沉降在空间变化的影响规律，获得了大面积堆载对周边环境影响的定量分析方法。任光明等[17]对斜坡岩体卸荷进行了分带量化，提出了具体的量化指标，并验证了该卸荷分带量化方法的可靠性。沈军辉等[18]对边坡应力场进行了测试，结果表明边坡应力场随深度变化具有明显分带性，应力场随着深度的增大不断增大。卢文波等[19]提出并论证岩体开挖荷载的释放为瞬态卸荷的观点，并指出高应力条件下的岩体开挖需要充分考虑荷载的瞬态特性及动力效应。以上研究为露天矿边坡开挖过程中应力-应变规律[20]的揭示提供了基础，也为节地减损开采技术的实现创造了条件。节地减损技术的研究可实现绿色理念与开采技术的融合，加快露天开采技术的绿色化进程。

笔者基于节地减损开采作业方案分析了端帮边坡高度和角度的变化规律，建立数值模型分析了靠帮开采、降段和内排回填过程中的水平应力、自重应力，同时获取了端帮边坡的稳定系数变化规律，为提高人员和设备的安全性，实现绿色理念与开采技术的融合，加快露天开采技术的绿色化进程提供参考。

1 节地减损开采模式及边坡结构变化规律

露天开采的基本作业程序是先将矿体覆盖层剥离掉，然后采出有用矿体，再将剥离物滞后于矿体开采位置一定距离的采空区进行回填。其动态演化过程是在“实体上构造空间”和在“空间上构造实体”，如图1所示。覆盖物的剥离和矿体开采打破了完整地层，破坏了原始地层中的应力平衡状态，造成了地应力的重新分布，频繁的高强度应力卸荷造成了围岩圈变形破裂，以及边坡的变形失稳[21-22]。

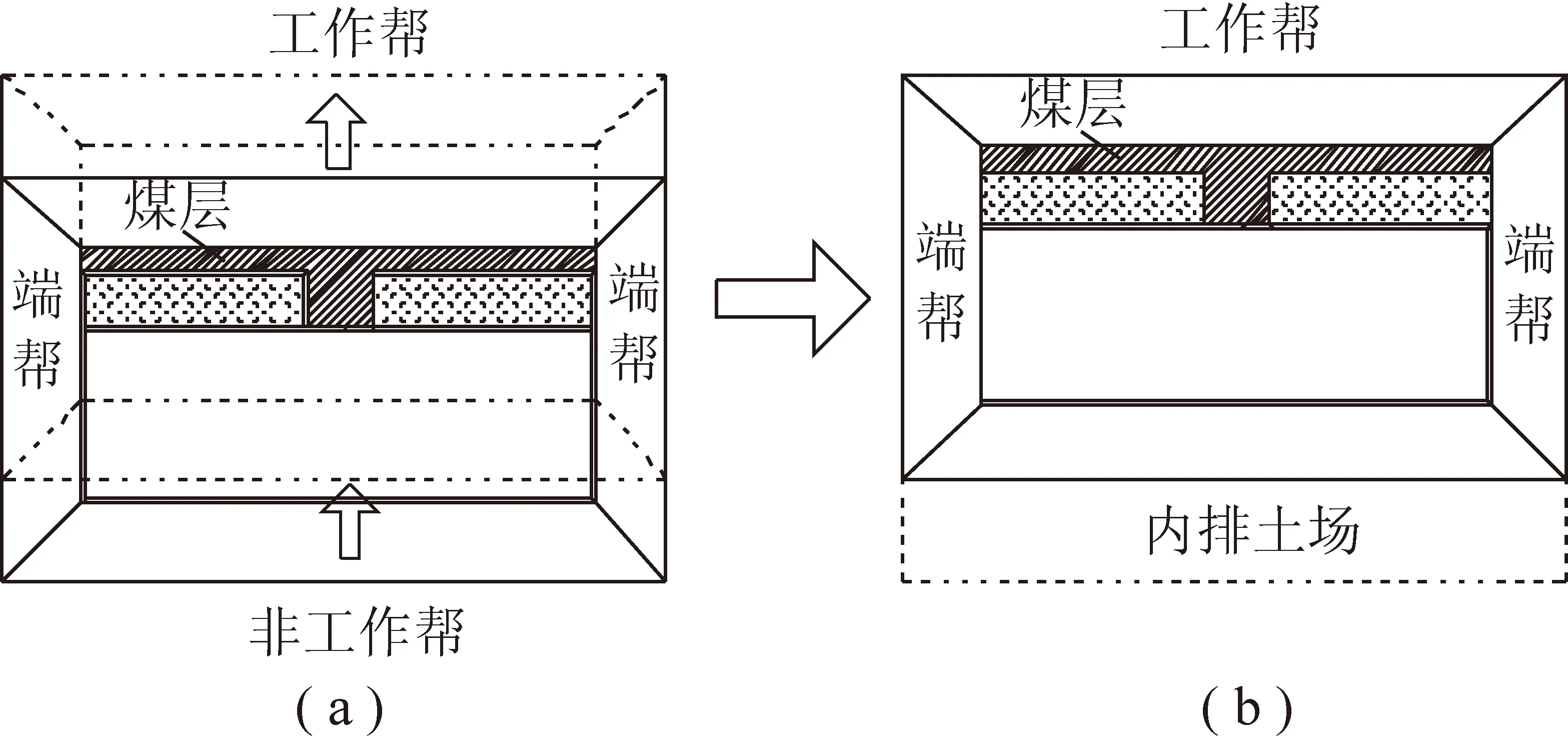
图1 采场推进示意Fig.1 Sketch map for stope advance schematic

从图1可以看出，露天开采时，工作帮以一定的速度向前连续推进，完成覆盖层的剥离和煤层的开采，推进至采场具有足够空间时，进行剥离物的内排作业。此时，露天矿的内排土场和工作帮便实现了动态追踪式的推进状态。对于采场端帮，其几何结构(角度)是影响矿区平均剥采比的重要指标。端帮角度越大，平均剥采比越小，如图2所示。对于地表境界固定的情况(图2(a))，在保证边坡在服务期限内稳定的前提下，坡脚由E点推进至D点，则需要剥离ABC区域，可回收BCED区域的煤炭资源，这一阶段的剥采比远小于矿区平均剥采比，因此，这种靠帮开采方式的经济效益显著。对于深部境界固定的情况(图2(b))，在保证边坡在服务期限内稳定的前提下，坡顶位置由D点收缩至E点，则损失ABC区域的煤炭资源，减少BCED区域的剥离量，这一区域的剥采比远大于矿山平均剥采比，因此，将地表境界向采场内部收缩，可以减少矿区用地面积，具有显著的社会和环境效益。

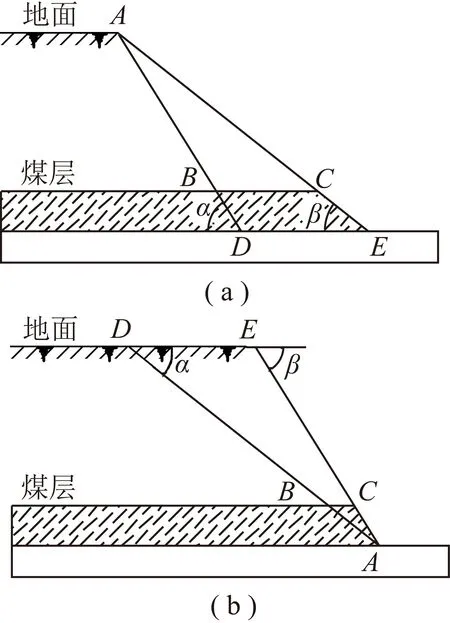
图2 节地减损开采方案Fig.2 Mining plan with land saving and ecological detraction

基于时效边坡理论开发的靠帮开采技术，可根据需要来提高经济效益或增加环境效益。将这一技术方案与绿色开采的理念相融合，提出节地减损开采方案，在矿区的建设之初和生产进程中有针对性的调整端帮参数，实现矿山经济效益和矿区环境的双赢。

2 边坡应力分异规律

2.1 边坡中的应力类型

露天开采改变地层结构时，影响的应力类型主要包括自重应力、构造应力和变异应力，这些应力在地层或边坡结构发生改变时相应的发生变化，属于感生应力。以下是对这3种主要应力的详细描述。

2.1.1自重应力

该应力的来源为岩体的自重，自重及泊松效应引起了侧向水平应力即为自重感生应力，其大小可按式(1)进行计算:

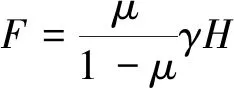
(1)

式中，F为自重感生应力，kN;γ为上覆岩体的容重，kN/m3;μ为泊松比;H为上覆岩体的高度，m。

由式(1)可知，当边坡岩性均一，即岩体容重γ和泊松比μ不变(可视为常量)，则自重感生应力F与深度H呈线性关系;对于非均质岩层，其容重γ和泊松比μ不相同，则仅能确定F与H成正相关，无法确定是否为线性关系。随着深度的不断增大，下部岩体所收到的重力较大，泊松效应也更加明显，如果存在软弱层，则会产生明显的塑性流变，诱发边坡变形失稳。

2.1.2构造应力

构造应力是板块运动相互挤压而蕴藏在岩体中的巨大能量。随着与板块挤压位置的不断增大，构造应力逐渐减小。我国境内地应力场有显著的发育规律，主要受印度洋板块和亚欧板块交界的影响，我国每个地区的最大主应力服从一定的准则，该点分别与我国的察隅和巴基斯坦的伊斯兰堡连线所成夹角，其角平分线方向近似为该点主应力方向。而各地最大主应力的量值则随上述两连线的夹角呈正比例变化。

2.1.3变异应力

变异应力是地壳运动过程中，岩浆侵入岩体造成物理和化学性质发生了较大的改变，变异应力的影响范围较小，仅影响其侵入区域的小范围。但是对于影响侵入范围之外较远的区域影响极小。

2.2 边坡内部应力分异机理

露天开采形成高陡边坡的同时，也破坏了地层的完整性及原始的应力平衡状态。由此引发了自重应力、构造应力及其他不平衡应力重新卸载，不平衡应力在寻找新的稳定结构体的过程中，其卸载作用会造成边坡临空面岩体变形、破裂甚至失稳。露天矿高陡边坡进行节地减损开采会再次形成不平衡应力卸载。由于边坡角度较大，不平衡应力在寻找稳定支撑结构时，其应力迹线的曲率不断减小，呈拱形结构退行，直至寻找到能够平衡该应力的岩体结构，此时，在完整应力迹线上部的岩体为卸荷造成的松弛、变形破坏区，如图3所示。

图3 边坡不平衡应力分异迹线Fig.3 Unbalanced stress trace of slope

当不平衡应力无法寻找到稳定岩体结构时，会造成岩体松弛破裂，直至滑面贯通形成运动型破坏。此时，下部滑体具备临空面条件，率先形成运动性破坏，滑体下部整体运动牵引上部岩体协同运动，整体表现为牵引式运动性破坏，其破裂结构如图4所示。下部滑动运动的位移达到一定程度之后，会在上部某个抗拉强度较低的位置形成拉裂面，至此滑体封闭圈形成，滑坡酝酿完成。

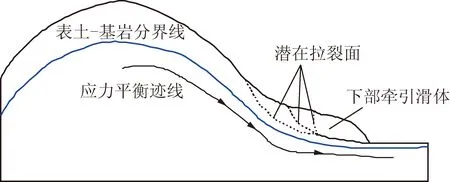
图4 不平衡应力分异过程的牵引式渐进破坏Fig.4 Pull-type progressive failure during the process of unbalanced stress differentiation

2.3 降段过程的应力分异规律

基于边坡内部应力类型和开采造成的几何结构变化，分析了应力分异规律和边坡潜在的破坏状态，为了进一步揭示节地减损开采模式下，边坡内部的应力随开挖深度、边坡角度的变化规律，采用三维数值模拟方法进行分阶段模拟，然后统计不同状态下的峰值应力，回归分析在开挖降段、靠帮开采过程中的应力变化规律。

以蒙东草原区某露天煤矿采场端帮形成和发展过程为依据，建立三维模型，模拟分析开挖降段、靠帮开采过程中的应力分异规律。为了防止地层产状影响本研究对于露天矿采动过程中应力分布普遍规律的认识，特对地层产状和数量进行了简化处理，边坡模型如图5所示。其中图5(a)为露天矿采场形成和发展示意图，图5(b)，(c)分别为采场降段过程、靠帮开采的变化示意图。边坡中所含岩层及物理力学参数见表1。根据排弃物受到上覆压力的差异，按照50 m对其进行分层，每层的物理力学参数见表1。

图5 采场开挖降段及靠帮开采示意Fig.5 Excavation depth decline and steep mining of the mining stope

表1 边坡岩体物理力学参数
Table 1 Physical and mechanical parameters of rock mass in slope

岩性内摩擦角/(°)黏聚力/kPa容重/(kN·m-3)剪切模量/MPa体积模量/GPa弹性模量/MPa端帮406021.31004960基底334022.5303550排弃物-Ⅰ362015.5201835排弃物-Ⅱ362216.0222138排弃物-Ⅲ362517.1252542排弃物-Ⅳ362918.2303047排弃物-Ⅴ363419.5383752排弃物-Ⅵ364021.0504557

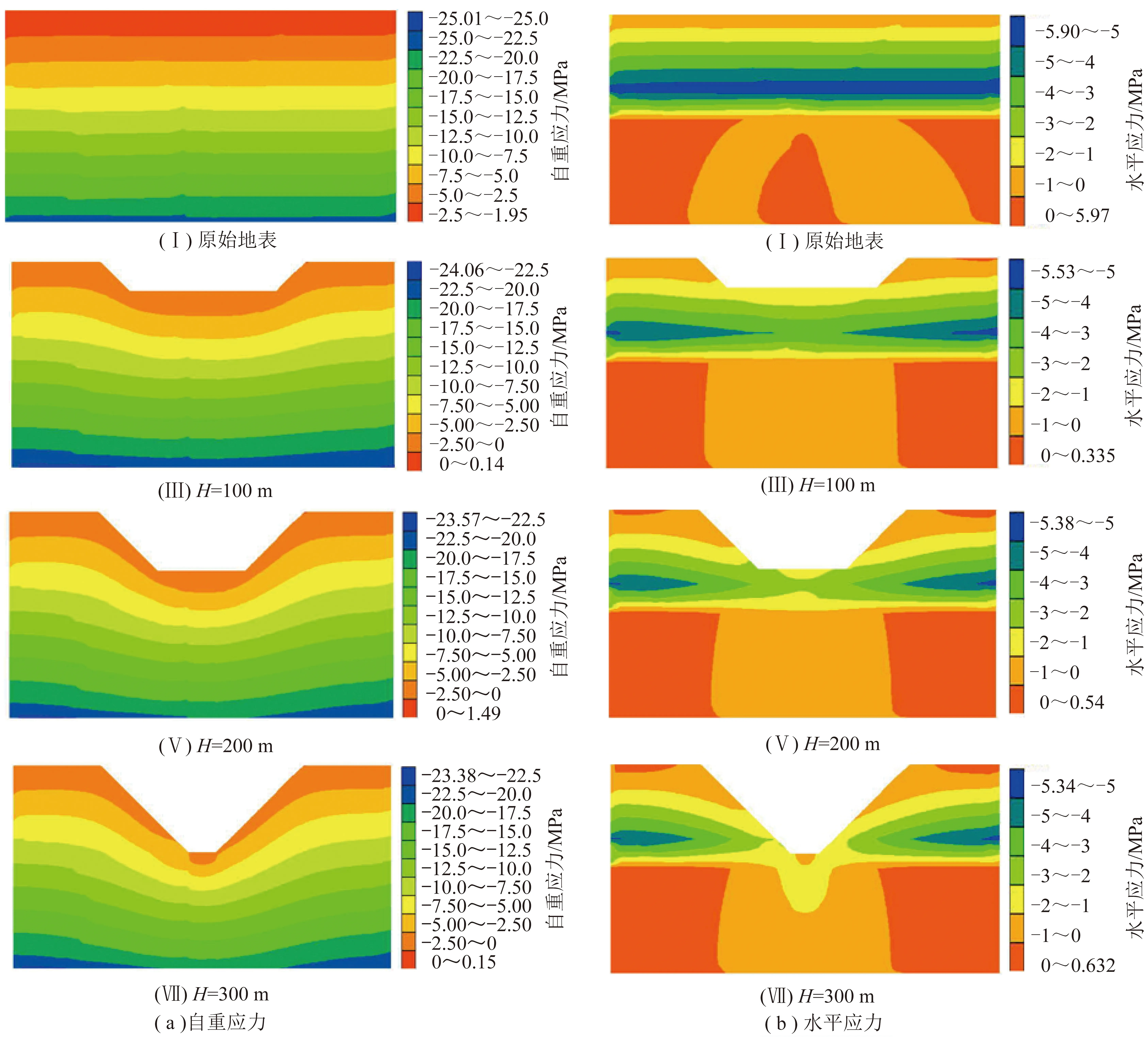
图6 不同开挖深度的应力场分异规律Fig.6 Stress differentiation rules with different excavation depth

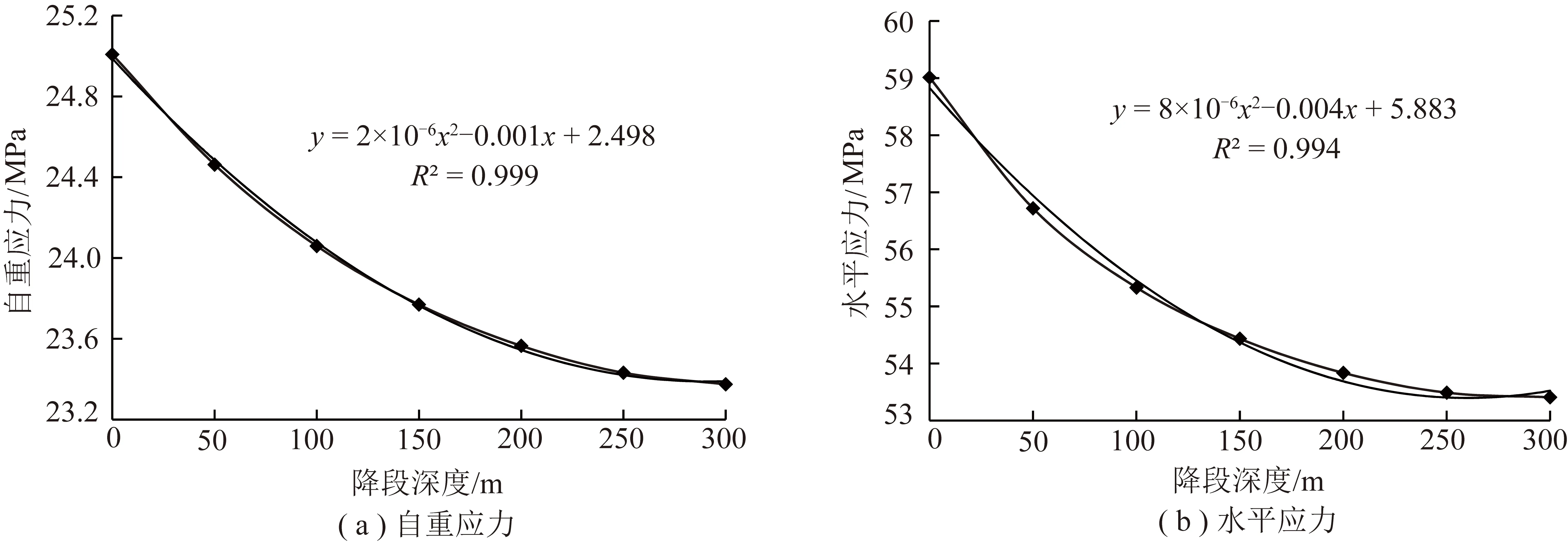
图7 降段过程不同峰值应力波动曲线Fig.7 Different peak stress curve during excavation depth decline process

对构建的边坡三维模型进行分步开挖降段、分步靠帮开采，并分析开挖降段及排土过程的稳定性。具体的分析指标包括自重感生应力、水平感生应力、边坡稳定系数等。按照采矿程序发展规律，逐步向下开挖，每次开挖深度为50 m，逐步形成高陡端帮边坡，不同边坡高度H状态下的自重感生应力云图组如图6(a)所示，水平感生应力结构如图6(b)所示。

从图6(a)可以看出，随着降段开挖的深度不断增大，不平衡应力的卸荷深度逐步增大，卸荷的次数也不断增多，随着深度的增大，自重感生应力的量级也不断增大。露天开采造成了地表的起伏，也诱发了自重感生应力出现顺地形下凹，且凹型曲率随着开挖深度的加大不断减小。随着开采深度从0 m增加至300 m，采场下部基底位置的自重应力下降了1.6 MPa左右，整个开挖降段过程中，自重感生应力的峰值呈二次函数降低，且下降的速度逐渐放缓，如图7(a)所示。

从图6(b)可以直观看出，水平感生应力在开挖过程中的变化规律更为明显，完整岩体被破坏之后，水平应力卸荷是造成边坡临空面岩体变形破裂的主要动力源。边坡内部形成了以采场中心线为轴的对称“楔形”应力结构，开采深度越大，楔形体的曲率半径越小。“楔形”应力的中心峰值应力随开采深度呈二次函数递减，下降的速度逐渐降低，根据回归分析，得到中心峰值应力F(对应变量y)与开挖深度H(对应变量x)的函数关系为:y=8×10-6x2-0.004x+5.883，(R2=0.994)，二次函数曲线如图7(b)所示。

在开挖降段的过程中，不同端帮高度的岩体自重压力产生的水平应力可按式(1)进行计算，此时水平应力与端帮高度H满足线性正相关。随着端帮高度的增大，其边坡底部的有效阻抗长度Lr也呈线性增长，端帮边坡底部岩体提供的有效抗剪强度可按式(2)进行计算:

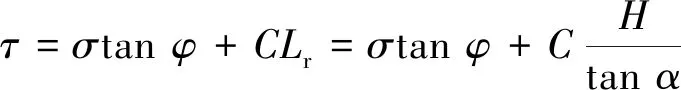
(2)

式中，σ为边坡上部的正压力，kN;φ为岩体的内摩擦角，(°);C为端帮岩体的黏聚力，kPa;Lr为端帮边坡底部的有效阻抗长度，m;H为端帮边坡高度，m;α为端帮边坡角，(°)。

边坡上部的正压力σ由上部岩体的重力提供，其大小可按照下式进行计算:

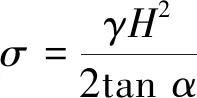
(3)

将式(3)代入式(2)，即可得到端帮底部岩体提供的有效抗剪强度，该强度与自重感生应力进行合成之后，得到水平应力的计算公式为

(4)

由式(4)可知，水平应力是关于端帮高度H(降段深度)的一元二次函数，与数值模拟分析得到的函数关系一致。

2.4 靠帮过程的应力分异规律

端帮角度是影响边坡内部应力的另一个重要因素。靠帮开采过程中，端帮角度不断增大，不平衡应力的卸荷量级也随之增大。为了揭示靠帮开采过程中，边坡内部自重和水平应力的变化规律，保持相同的端帮高度(300 m)，以2°为1个步长，将端帮边坡角度从37°逐步提高至45°，分析得到了不同角度时的自重应力和水平应力分布云图，如图8所示。

图8 不同端帮角度下的应力结构Fig.8 Stress structures of different end-slope angle

统计图8中不同端帮边坡角度所对应的最大自重应力和水平应力，进行回归分析，得到自重应力和水平应力随端帮边坡角度的增大呈二次函数递增，具体的拟合曲线如图9所示。

图9 靠帮过程中的峰值不同应力波动曲线Fig.9 Peak gravity stress curve during steep mining process

通过对开挖降段和靠帮开采过程中的自重和水平感生应力分析，得到了不平衡应力的分异和发展规律。开挖深度和端帮角度的增大会降低应力拱顶部的曲率，形成较强的压力拱效应。“楔形”水平应力结构始终作用于坡脚位置，长期的卸荷作用会造成边坡“底臌”和切出，对端帮稳定性起着关键性影响作用。

3 端帮时效稳定系数发展规律

3.1 采排工程中的端帮稳定性评价

对于分区开采的露天煤矿，其工作帮的剥离工程与采空区的排土工程互为逆过程。工作帮剥离在形成大型空间，而内排作业在消除大型空间。在采场逐渐形成的过程中，边坡高度不断增大，稳定性渐进退化，表现出显著的时效特性。根据图10中的采排工程动态发展示意图可知，采场达到最大深度时，高陡端帮完全形成，随着工作帮不断向前推进，内排土场在工作帮推进方向的后侧临空面开始内排，内排土进入发展阶段，随着内排土场的不断跟进，分析位置(A—A剖面)的端帮高度不断降低，直至完全消失。

图10 采排工程动态发展示意Fig.10 Sketch map for dynamic development of mining and dumping engineering

根据图10中的采排发展过程和端帮边坡结构建立三维分析模型，通过三维模拟分析，得到开挖过程中(每步开挖深度H=50 m)的稳定性分析结果如图11所示。内排作业压覆暴露的高陡端帮，降低端帮边坡整体高度。在这一过程中，端帮边坡稳定性不断提高，模拟分析得到不同排土步骤(每次内排高度HI=50 m)时的稳定性如图12所示。

统计开挖过程和排土过程中端帮边坡的稳定系数，并绘制稳定系数变化曲线，如图13所示。

由图11和图13(a)可知:随着开挖深度的加大，端帮边坡塑性区范围和剪应变量级不断增大，稳定系数呈负指数规律递减，回归分析得到端帮稳定系数与边坡高度的耦合关系为:f=16.27H-0.53(R2=0.994)。在露天矿的初期开挖阶段，边坡稳定系数下降较快，但是，由于稳定系数的初始值较大，因此，初期阶段未必会造成边坡失稳;随着边坡高度的继续增大，稳定系数下降的速度逐渐放缓，但是稳定系数值已经较小，因此，在这个阶段进行降段或者靠帮风险较大，需要结合稳定性评价谨慎处理，确保生产作业的安全。

由图12和图13(b)可知:排土作业过程中，端帮边坡稳定系数呈指数规律递增，与开挖过程的稳定性变化规律相反。由于排弃物的完整性和强度明显低于原始岩体，同等深度的内排回填后边坡稳定性要低于开挖边坡的稳定性。在排土场高度增加的过程中，底部排弃物料的强度不断提高，使得在内排高度不断增加的过程中，稳定系数增长的斜率比同等阶段开挖降段时稳定系数下降的斜率要大。

3.2 采排过程中应力和稳定系数的时效规律

露天矿的开挖降段和内排回填是一个动态的工程演替过程，这个过程的实施需要一定的时间，本文所研究的露天矿的具体几何尺寸和设备生产能力见表2。按照根据每个降段过程、排土过程的工程量计算所需的工程时间见表3。

根据表3中计算得到采排工程的时间进度情况，结合不同降段深度所对应的水平、自重应力大小和稳定系数的计算结果，可以得到自重和水平应力随时间的变化规律，以及时效稳定性的变化规律，如图14所示。

从图14可知，开挖降段过程中，自重应力和水平应力随工程时间的增长均呈线性下降，不同于按照降段深度拟合的规律。端帮稳定系数随着时间的增长呈二次函数规律下降，与稳定系数和降段深度拟合的负指数下降规律也有一定的差异;而排土过程中，稳定系数随时间的增长规律与之前的规律较为接近。综合以上分析可知，端帮内部应力大小和稳定性应该综合工程顺序和时间长度进行评价，确保其时效稳定性与工程环节及时间因素充分结合，提高时效评价的可靠度。

表2 露天矿几何参数和生产能力
Table 2 Mining geometry parameter and production capacity of open pit mine

表3 采、排工程的时间进度情况
Table 3 Time schedule of excavation and inner dumping

降段过程/m50100150200250300工程方量/Mm3226.41151.715111.58075.51943.45214.557降段工程时间/月18.8712.649.306.293.621.21内排工程时间/月22.6415.1811.167.554.351.46

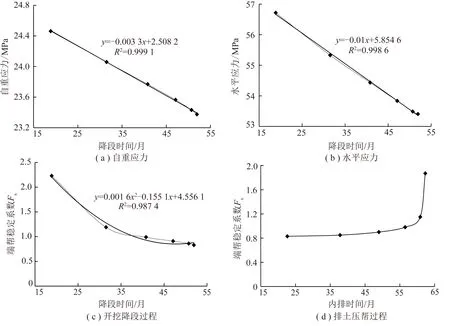
图14 采、排过程中端帮应力和稳定系数变化规律Fig.14 Stress and stability factor change rule in the process of excavation and inner dumping

4 结 论

(1)分析了适用于扩建和新建露天矿的2种节地减损开采技术方案；建立了降段或靠帮开采造成的不平衡应力分异模型及其诱发的边坡牵引式渐进破坏模型。

(2)采用数值模拟分析了节地减损开采过程中水平应力、自重应力和稳定性的变化规律。自重应力和水平应力均呈现以采场中心线为轴的对称结构；在采场范围内，自重应力呈拱形结构，水平应力呈“楔形”结构。

(3)从0～300 m的降段过程中，自重和水平应力的峰值呈二次函数下降，并分别降低了1.6 MPa和5.6 MPa。端帮从37°～45°的靠帮开采过程中，自重和水平应力的峰值呈二次函数规律增大。并分别提高了0.5 MPa和9.4 MPa。

(4)在开挖降段过程中，端帮边坡的稳定系数从2.23下降到0.83；其下降规律表现为随开挖降段深度呈负指数降低，随开挖时间呈线性规律下降。内排回填过程中，端帮稳定系数从0.83提高到1.87，稳定系数随内排回填高度、时间均呈现指数的增长规律。