智能汽车激光雷达和相机数据融合系统标定

许小徐，黄影平，胡 兴

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

智能汽车采用相机和激光雷达实现对环境的感知。通过这些传感器的数据融合，可以发挥各个传感器的特点提高环境识别的可靠性[1]。数据融合的前提是传感器的联合标定，标定就是要找到传感器坐标系之间的位置关系，据此可以将不同传感器的数据在空间上准确地对应起来。

现有的激光雷达和相机联合标定方法可以分为两类：特征点匹配法和棋盘格标定法。特征点匹配法采用特殊图形的标定板提取激光雷达采集到的三维点和对应的相机得到的二维图像点，建立约束方程，优化计算相机位姿，其本质是相机位姿估计的 PNP（perspective-n-point）问题[2-3]。该方法无需求解相机的内参数，标定精度主要取决于特征点对的提取精度[4-7]。刘大学[6]针对单线激光雷达，设计了一种带刻度的平面标定模板，利用激光雷达点拟合直线求交点，获得特征点坐标，再根据标定板上的刻度，手动标注出特征点位置，以便在图像中找出对应的图像坐标。该方法适用于单线激光雷达的标定，且需要手动标注特征点，易引入操作误差，且标定板制作过程复杂。Park等[7]针对32线激光雷达设计了一种三角形平面标定板，利用激光雷达扫描在标定板上的边缘点拟合直线方程，再利用直线的交点求出三角形的顶点作为特征点，对应图像中特征点采用图像角点检测的方法求出。该方法仅适用于32线或者扫描层数较多的激光雷达，对于四线激光雷达，可供拟合的边缘点数量少，所以拟合出的直线误差会很大；并且由于提取的是边缘点，对激光雷达的扫描角度分辨率要求较高。基于棋盘格的标定方法最早由华盛顿大学机器人研究室Zhang等[8]提出，通过相机和雷达多角度观测棋盘格平面，利用棋盘格平面在两个坐标系的一致性，根据约束条件用线性方法求解外部参数，再用非线性方法[9-10]进一步优化。Osgood等[11-12]详细介绍了Nelder-Mead优化方法在激光雷达和相机标定问题上的应用。项志宇等[13]基于Zhang等[8]的方法做出改进，采用平面拟合增加了方法的鲁棒性。该类方法只能标定外部参数，相机的内参数要采用张正友法[14]求解。

2018年三季度，根据中怡康推总数据，洗衣机总体零售量规模为797万台，环比下降8.3%；零售额达到153亿元，同比上涨2.6%，环比下降10.5%。在家电行业整体低迷的环境下，洗衣机是三季度唯一实现增长的大家电品类，实属珍贵；在零售量8.3%的降幅下能够实现零售额2.6%的增长，也展示出洗衣机行业结构升级的成果已经显现。

本文对特征点匹配法以及棋盘格标定方法都进行了研究。针对Park等[7]的方法对激光雷达的层数和扫描角分辨率要求较高的不足，设计了一种新的标定模板，利用平面拟合的方式求取特征点，获取的特征点更加可靠。棋盘格法借鉴了Zhang等[8]和项等[13]的方法，针对他们没有通过实验验证标定精度的不足，本文设计了对标定结果的标靶验证实验，采用靶标在图像上实际的对准效果来验证标定结果的准确性。

1 融合系统标定原理

图1为激光雷达坐标系OC-XCYCZC、相机坐标系OL-XLYLZL和图像坐标系O-XY之间的关系。θx，θy，θz为激光雷达坐标系相对于相机坐标系在x, y, z方向的旋转角度，（cx，cy，cz）为平移向量，（u0，v0）为图像中心的像素坐标，f为相机的焦距。

设空间中一点P在激光雷达坐标系坐标为（XL，YL，ZL），在相机坐标系坐标为（XC，YC，ZC），则有

由图3可知，NL与NC的长度差应当等于平移向量T在NL上投影的长度，即

图1 各坐标系关系图Fig. 1 Diagram of related coordinate systems

设P对应的图像坐标为（u,v），则有

式中：dx和dy表示图像中1个像素在x和y轴方向的物理尺寸；，是相机的内参数矩阵。

将式（1）代入式（2）可得

就这样，他们和我见了面。见面之后，他们觉得我不仅有知识有学问，还具备良好的修养，更难能可贵的是我才刚刚24岁，而且家境贫寒急需用钱。他们认为我会是一个称职的“代孕妈妈”。而我得知了陈清夫妇的坎坷遭遇，看着这对经历了太多磨难的夫妻饱含希冀的眼神，不禁欣然同意为他们孕育孩子。

（5）以式（18）为代价函数，采用LM优化方法，优化初始解。

2 基于特征点的标定方法

2.1 特征点标定方法原理

为了提高平面的拟合精度，应有足够多的激光雷达点，因此在制作标定板的过程中，应尽量使得标定板的尺寸足够大，从而使每个平面上有足够多的激光扫描点，本文中标定板大小为1.2 m×2.4 m。且在取拟合的散点时应尽量避免取靠近两个平面结合处的点，以保证所取的点位于同一个平面。

根据构架及轮对垂向受力可列出静力学平衡方程，结合4个轴箱变形协调条件可求得转向架4个轮轮重大小FWi(i=1,2,3,4)，如式(2)所示。

将式（6）代入式（4）和式（5）得到两个方程

也就是说一对特征点可以建立两个方程。设有n组特征点，则可建立2n个方程：

式中A12*1= [n11，n12，n13，n14，n21，n22，n23，n24，n31，n32，n33，n34]T，一组特征点对应两个方程，求解12个未知数，至少需6组特征点。通常会多取几组特征点，形成过约束方程组，用线性最小二乘法求解[15]。

2.2 特征点标定方法步骤

特征点选取的关键是能够可靠地找到激光扫描点和与之对应的图像点。为了做到这一点，本文设计了一种标定板，如图2所示。标定板上存在图中1，2，3，4四个平面，其中平面2，3向后折叠，分别与平面1，4形成一定夹角。图中横向的粗实线，细实线，点划线，虚线为模拟的四层激光雷达的扫描线，P1，P2，P3三个顶点为待求取的三个特征点。

在班级群里，通过每日“家长作业”的展示和主题交流，家校沟通不再是教师喋喋不休的讲解、劝导，而是与家长一起陪伴孩子成长进步。人人会说话，人人有话说，人人想说话，这就是微信群的聊天姿势。我们要在班级智慧的群聊中加深情感、交流信息、增强信任、共同提高，真正实现家校合作，共同助力孩子的幸福成长。

图2 特征点法标定板实物图Fig. 2 Calibration template of feature-point method

具体步骤如下：

（3）对每个位置激光扫到棋盘格上的点进行平面拟合，按照式（15）求出每个位置的NL。

设空间平面方程为Ax+By+Cz+D=0，利用各个平面的激光雷达点，采用线性最小二乘法拟合出4个平面方程Aix+Biy+Ciz+Di=0，其中i表示第i个平面。显然P1点为4个平面的交点，即P1坐标满足如下方程组：

采用线性最小二乘法可求解P1的坐标。

根据各个平面的方程可知，其对应的法向量 Vi为（Ai，Bi，Ci），其中 i表示第 i个平面。根据向量叉乘的定义可知，向量应与V1×V2共线，再结合向量的模，即可求出该向量。

（2）提取特征点图像坐标

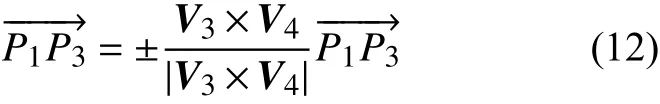
设点 P1，P2，P3的坐标分别为 p1，p2，p3，则有

一眼看下去，很明显，南边的十几岁那个团队的少年们，一个个都凝神静气、呼吸自然。同时一个个都做到了‘深、平、稳’。很显然在‘蕴气式’上都有了一些成就。

同理可知，

在图像中采用角点检测的方法，获得标定板的三个顶点在图像坐标系中的坐标。从而获得三组对应的特征点。

（3）移动标定板的位置，再次求出三组特征点，用六组特征点，按照式（9）建立方程组，用最小二乘法[15]求解矩阵A12*1。

通过提取若干对激光雷达与图像特征点，建立约束方程组，求解矩阵A中的12个元素。式（3）展开可得

3 基于棋盘格的标定方法

3.1 棋盘格法标定原理

如图3所示，NC与NL分别代表从相机坐标系原点和激光雷达坐标系原点到棋盘格平面的三维垂直向量，NC的模|等于从棋盘格到相机原点的距离，NL的模|等于从棋盘格到激光雷达原点的距离。

1) 间歇采样重复转发干扰只要获得脉压雷达的最小脉宽就可实施有效干扰，因此不需要进行过多的电子战侦察工作，效率更高；

通过张正友标定法[14]求得世界坐标系（棋盘格左上角为原点）到相机坐标系的旋转矩阵R′，以及平移向量T ′，则有

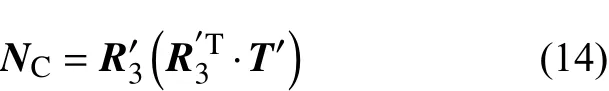
式中 R′3表示 R′ 第三列。

NL通过激光雷达点云拟合平面获得：采用最小二乘法[15]对激光扫到棋盘格平面上的点拟合平面，设拟合出的平面方程为Ax +By +Cz +D=0，则（A，B，C）为平面法向量，且（A，B，C）为单位向量，则

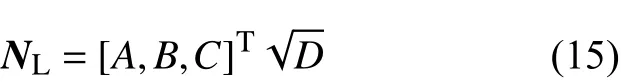
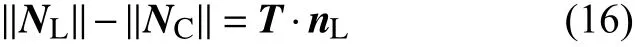
式中nL是NL的单位向量,一组给定的NL与NC提供一组求解T的约束条件，改变棋盘格平面位置，提供多组NL与NC，用线性最小二乘法[15]求解T。

陆游的地域书写，比其他作家受时空转换的影响更明显。钱钟书云：“至放翁诗中，居梁益则忆山阴，归山阴又恋梁益，此乃当前不御，过后方思，迁地为良，安居不乐；人之常情，与议论矛盾殊科。”在时间的流逝与空间的转变中，陆游关于梁益的地域书写在内容和情绪等方面都发生了不小的变化，而有些变化因记忆模糊或创作心态改变甚至会前后矛盾，虽非“议论矛盾”，却是许多细节或情绪上的矛盾。

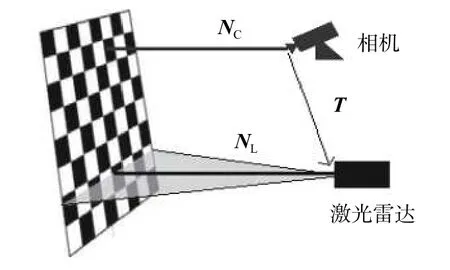
图3 棋盘格法标定原理示意图Fig. 3 Principle diagram of planar checkerboard method

根据坐标系的变换原理可知，nL在相机坐标系下可以表示为RnL，设NC的单位向量nC,

由RnL与nC平行关系可知，向量RnL与nC的内积为1，即

实证研究结果显示：同样是每提高1个单位，成长性创业质量比生存性创业对农民工价值观念、身份认同、经济适应和生活方式因子得分的促进作用分别高出3.952分、3.028分、4.742分和2.096分。虽然大多数农民工返乡创业的投资规模较小，大多数选择在离家较近的小城镇创业，以达到重新整合配置返乡农民工人力资源，扭转以往返乡陷入水平流动或向下流动的困境，并进一步通过返乡创业实现积极的向上流动，但总体来说，现阶段农民工返乡创业的质量普遍偏低，大都处于创业后的发展阶段，有些甚至处于停滞或倒退阶段，其创业所获得的利润往往不足以维持其在城市体面的生活，因而生存性创业质量对其就地市民化的影响程度相对较小。

式中：Ncr为液化判别标准贯入锤击数临界值；N0为液化判别标准贯入锤击数基准值，可按表4.3.4采用；ds为饱和土标准贯入点深度，m；dw为饱和土标准贯入点深度，m； ρc为粘粒含量百分率，当小于3时或为砂土时，应采用3； β为调整系数，设计地震第一组取0.8，第二组取0.95，第三组取1.05。

一组给定的nL与nC提供一组求解R的约束条件，改变棋盘格平面位置，提供多组nL与nC，用线性最小二乘法[15]求解R。

将以上得到的R,T作为初始解，建立式（18）所示目标函数，使用Levenberg-Marquard（LM）优化方法[8]对初始解进行优化。

式中：n表示放置的棋盘格位置数；m表示第i个位置棋盘格上的激光扫描点数。NC,i代表第i个棋盘格位置时相机原点到棋盘格平面的垂直三维向量。Pi,j表示第i个位置的棋盘格上的第j个激光扫描点。

将旋转矩阵转化为旋转角，公式为

式中rij表示R第i行第j个元素。

3.2 棋盘格法标定步骤

（1）将棋盘格放置在相机和激光雷达共同视场的20个不同位置。

（2）用张正友法求取每个位置棋盘格相对于相机的旋转和平移矩阵，可采用MATLAB标定工具[16]实现，根据式（14）求出每个位置的NC。

（1）提取特征点在激光雷达坐标系的坐标

（4）按照式（16）和式（17）建立约束方程组，用线性最小二乘法[15]求出R,T初始解。

因此将激光雷达测量点（XL，YL，ZL）对应到图像点（u,v）的问题，转化为求取10个参数（cx，cy，cz，θx，θy，θz，u0，v0，fx，fy），或者求解矩阵A的过程。下述基于特征点的标定方法是求解A, 基于棋盘格的标定方法是直接求解10个参数。

（6）用张正友标定方法求取相机的内参数u0、v0、fx、fy。

4 实验结果

激光雷达和相机的安装位置如图4所示。激光雷达为四线激光雷达，水平视野为120°，扫描垂直视野为3.2°，角度分辨率为0.25°。标称的相机内参数为：图像分辨率640 ×480 ，焦距800 像素（6 mm），像素物理尺寸大小 7.5 μm。棋盘格标定板采用9×7格，每格大小为171 mm×171 mm。

④ manus dara-a sara-yin arbad-iyar yabuy-ageju bui(我们下月十来号就要走)

4.1 特征点法

按照2.2节描述的方法提取至少6组激光雷达和对应图像特征点坐标，计算得到的矩阵A如表1所示。

再次，每学年进行全区统一检测，为进一步研究提供数据。各校以“阅读实验校”评选为契机，以阅读为突破口，积极开发阅读课程，鼓励各学科根据学科特色开展相应的阅读研究活动，形成“大阅读”的理念，促进各学科均衡发展，形成“大教育观”，着力培养学生的综合素质，提升学校的综合实力，让学校成为真正的“书香圣园”。

幼儿园阶段的行为规范要求总体较自由和生活化，刚性要求较少。如入园和离园的时间不硬性固定，上课可以在不影响秩序的情况下去喝水或上厕所。随着一入小学，规范要求一下从宽松到严格，不迟到不早退，上课不能随便说话、上厕所，这些变化必然给孩子造成一定的心理压力。

图4 相机与激光雷达安装位置图Fig. 4 Installation diagram of the lidar-camera system

4.2 棋盘格法

按照3.2节所述方法，将棋盘格放置在20个不同位置，记录每个位置扫在棋盘格上的激光点Pi,j，求取每个位置的NL与NC,部分数据记录如表2所示。如3.2节所述，先用最小二乘法[15]求出R，[cx，cy，cz] 的初始解，在初始解的基础上进一步用LM方法[8]优化初始解，得到优化解，结果如表3所示。R与旋转角θx，θy，θz的转换按照式（19）求得。

教师应树立“大语文”的观点，让学生从传统那种“学海无涯苦作舟”的苦读走向开放型的自主学习。从课堂走向课外，从校园走向校外，使语文成为一泓活水，在丰富多彩的社会生活中学语文，长才干，学做人。因此，教师要引导学生深入生活，也可开展课外阅读活动，设立图书角，推荐好书让学生阅读，教给阅读方法，开展读书竞赛，兴趣小组等。在实践中出真知，让学生多观察，多思考，充分发挥学生的主观能动性。

4.3 校准结果验证

如图5所示，采用9个如图中标号1～9所示的细小白色泡沫靶，用可上下移动的细杆支撑，放置在相机和激光雷达共同视场。移动标靶使得激光雷达能够扫描到靶子上，记录各个标靶的雷达点坐标，同时在图像中取标靶图像的中心位置代表靶标位置，读取图像坐标，如表4所示。

表1 实验提取的特征点对与计算结果Tab. 1 Extracted feature points and calculated parameters

表2 棋盘格平面在部分位置的NL，NC及相应位置的部分Pl点坐标示例Tab. 2 NL, NC of the checkerboard planes at different positions and Pl at corresponding positions

表3 参数求解结果Tab. 3 Results of the parameters

图5 验证实验示意图Fig. 5 Diagram of validation experiment

分别采用特征点法和棋盘格法得到的结果，将激光雷达坐标投影到图像上得到投影的图像坐标，按照式（20）计算投影对准误差，记录如表4所示。

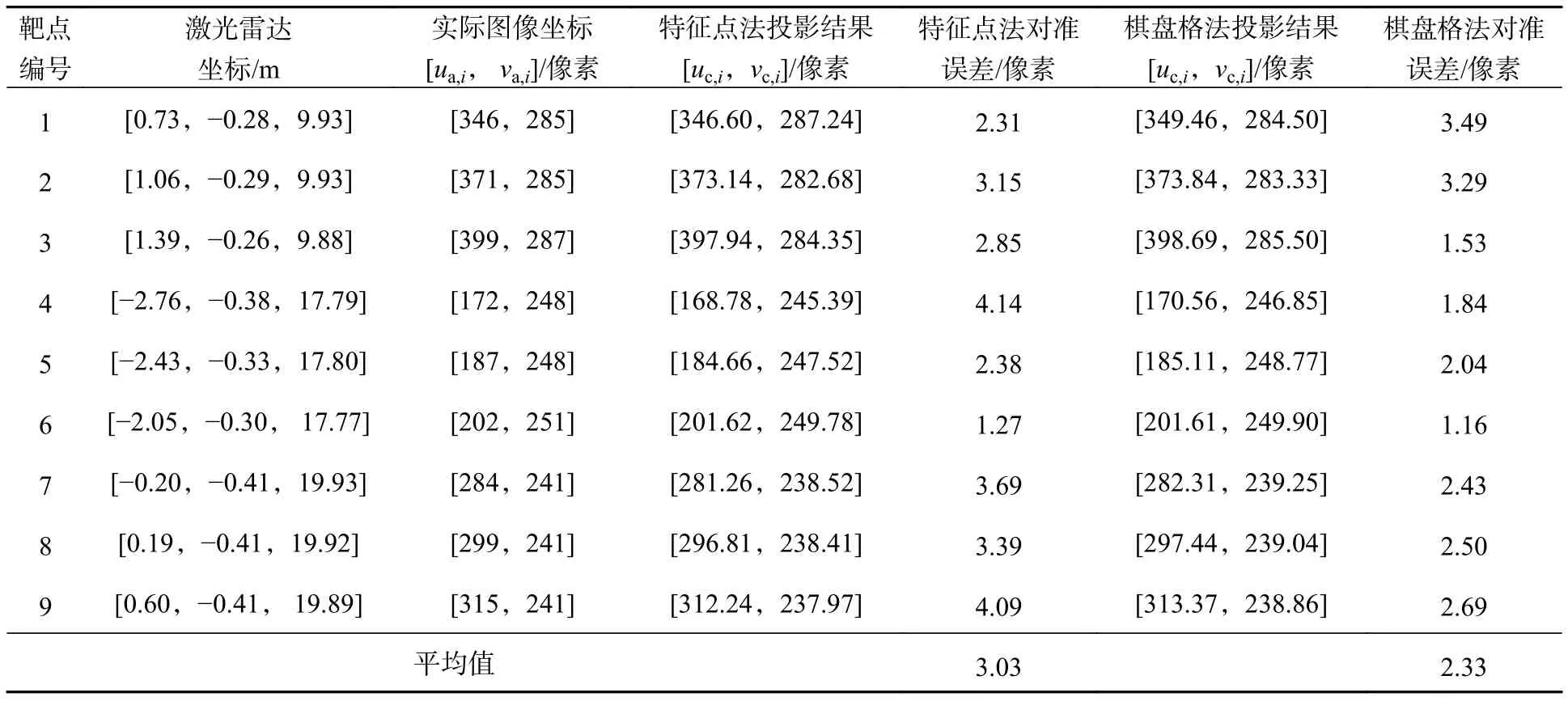
表4 特征点法与棋盘格法投影激光雷达点到图像坐标的结果Tab. 4 Results of the projection of the two methods

式中[ua,i，va,i] 表示第i个标靶实际读取的图像坐标；[uc,i，vc,i]为采用标定结果通过坐标转换得到的图像坐标。计算出特征点法的平均误差3.03 像素，棋盘格法的平均误差为2.33 像素。

将激光雷达点云数据分别依据两种方法的实验结果，投影到图像中，如图6所示，可见两种方法的激光点云都能很好地与图像匹配。

图6 投影激光雷达点到图像Fig. 6 Projection of lidar points to image

5 结 论

特征点标定法可以直接求出标定结果，其结果是一个包含了坐标系外参数和相机内参数的矩阵，利用该矩阵可以将激光雷达坐标转换为图像坐标，但是矩阵内各个参数的物理意义不明显。该方法的核心是准确提取特征点，本文设计的特征点选取方法相对于文献[6],省去了人为标注的过程，特征点选取也更为可靠、简单。相对于文献[7]拟合直线求取特征点的方法，本文采用平面拟合的方法求取特征点，可供采用的激光点数量显著增加，而且可以均衡激光雷达本身的测量误差引起的标定误差，提高了标定的精度。棋盘格法的标定过程需要分两步进行,即分别求取坐标系外参数和相机的内参数，其中相机内参数通过张正友标定法获得，坐标系外参数可以直接获取旋转角度和平移参数。棋盘格法无需人工标注特征点，避免引入手动误差。但是操作过程比较繁琐，需要将棋盘格标定板放置到多个不同位置，处理的数据也比较多。总之，两种方法各有优缺点，实验中棋盘格法的精度略高于特征点法。