Kinetic analysis via mathematical modeling for ferrous iron oxidation in a class of SBR-type system

Edgar N.Tec-Caamal,Refugio Rodríguez-Vázquez,Luis G.Torres-Bustillos,Ricardo Aguilar-López,*

1 Center for Research and Advanced Studies of the National Polytechnic Institute,Av.Instituto Politécnico Nacional No.2508,Colonia San Pedro Zacatenco,C.P.07360 Ciudad de México D.F.,Mexico

2 Interdisciplinary Professional Unit of Biotechnology-National Polytechnic Institute(UPIBI-IPN),Acueducto s/n,La Laguna Ticomán,Gustavo A.Madero,07340,Ciudad de México,Mexico

Keywords:Bifurcation analysis Hydrogen peroxide Iron oxidation Modeling Simulation

ABSTRACT This paper analyses the oxidation of ferrous iron via chemical and biological means in a class of Sequential Batch Reactors(SBR-type).For this,a kinetic model for the study of iron oxidation system is proposed,followed by a parametric sensitivity analysis and a bifurcation analysis,which allow selecting the most influential kinetic parameters in order to ensure a suitable prediction capacity of the mathematical structure.The system consists of two SBR bioreactors,the first being used to produce hydrogen peroxide(H2O2)that is fed to a second reactor where the iron oxidation is carried out by chemical-biological processes.Model predictions were compared with experimental data for the production of H2O2and for ferrous iron oxidation,finding suitable correlation coefficients(r2＞0.98)for each state variable.The bifurcation analysis showed the trajectories of the main variables,such as,biomass,H2O2and ferrous iron,under the change of the most influential kinetic parameters.This analysis demonstrates the usefulness of the constructed model to predict the kinetic behaviour of the SBR-type process.

1.Introduction

The production of hydrogen peroxide and the oxidation of ferrous iron by bacteria are well-known in the literature[1,2].As a coupled process they can present interesting properties[3,4].The importance of the first one is based on the high oxidizing strength of H2O2(0.695 V),which oxidizes a wide range of pollutants of environmental concern.The interest of the latter is due to the modification of the oxidation state of Fe2+since this property facilitates its removal by physicochemical techniques,or its immobilization by joining it to other compounds such as sulfur or arsenic by biological processes[5,6].On the one hand,bacterial species of Lactobacillus are known to be suitable producers of H2O2[7]and have been cultivated in aerated bioreactors using a wide range of carbon sources[2,8].Although lactic acid bacteria could be cultivated under aerobic conditions,this does not imply that oxygen is used in its energetic metabolism,but it can affect its physiology,by inducing an oxidative stress that seems to be key to obtaining an overproduction of H2O2,since the oxidative enzymes(such as pyruvateoxidase or NADH-oxidase)of these microorganisms reduce oxygen,probably due to a detoxification mechanism[7,8].On the other hand,the oxidation of ferrous iron carried out using chemical and biological methods simultaneously have presented an interesting performance in bioreactors[3,9].For instance,in the iron oxidation realized by H2O2and bacteria in the same container,the microorganisms act as a catalyzer since the oxidation of ferrous iron under acidic conditions is slow,moreover the use of high concentrations of H2O2(low molar ratios of Fe2+/H2O2between 0.33 and 33)may lead to an oxidative stress/damage to the microorganism[10].Bacterial species of the genera Acidithiobacillus,Thiobacillus,Sulfolobus,among others,are reported to be iron-oxidizing microorganisms,which can carry out several redox reactions to transform ferrous iron into ferric iron,which in turn may be delivered from the cell to the aqueous medium to avoid precipitation[1].

Computational modeling of bioprocesses is a useful tool that aims to develop predictive and explanatory models for describing complex systems[11],which in many cases vary under different conditions.This requires the construction of a mathematical structure that considers the phenomenology of the case study as much as possible,since the complexity of describing metabolic pathways as well as measurements in vitro may lead to inaccuracies[12,13].Once a model has predicted the behaviour of the experimental data,it can proceed to realize further analyses to improve the certainty and confidence of the model predictions,which commonly includes identifiability,uncertainty quantification,and sensitivity analysis[11].The last one is performed using a local or global sensitivity analysis,which consists of perturbing one or more parameters and comparing the simulations with a reference output[14].

A bifurcation of a dynamical system of the form ˙x=f（x，ω），xϵRn，ω∈Rk，takes place when one or more of these parameters(ω)change.It causes a modification in the qualitative structure of the solutions of the equations[15].In other words,this analysis evaluates the effect of parameter changes on the variables of interest.Moreover,to provide and establish a proper methodology to obtain a predictable model structure for any bioprocess,the sensitivity analysis may be complemented with a bifurcation analysis by using the most sensitive model-kinetic parameters as bifurcation parameters.It is important to note that there is a lack of information about this kind of analysis in the literature,which this study aims to remedy.In our study case,hydrogen peroxide production by bacteria has been described by mathematical approaches[2],as well as the iron oxidation by chemical and biochemical processes[9],however there is scarce information about the study of both processes analyzed as a sequential procedure,which can allow the successful oxidation of a wide range of metal pollutants.Due to the paucity of information about the two points described above,the study of this system from the point of view of kinetic analysis turns out to be necessary to generate reliable simulated data that allows performing further studies,such as reactor design,scale-up,optimization or control of the process.

This paper aims to offer significant kinetic insights into an SBR-type system for ferrous iron oxidation by developing a kinetic model validated with experimental data and performing subsequent analyses,namely,a sensitivity analysis coupled with a bifurcation analysis to assess the predictive capacity of the model.

2.Methodology

2.1.Mathematical model development

A phenomenological mathematical model was constructed based on classical mass balance approach to describe two processes configured as a sequential batch reactor.This coupled process consists of the batch operation of a first reactor for the production of H2O2by bacteria and a second bioreactor for the final oxidation of ferrous iron(Fe2+).An overview of the process is depicted in Fig.1.

Our approach involves the modeling,sensitivity analysis,simulation and a final bifurcation analysis considering the most influential parameters in order to analyze the mathematical potential of the model to describe the different operational conditions of each reactor of the process,using the initial conditions and experimental data reported elsewhere[2,8,10,16].A set of differential equations were developed to simulate the H2O2production reactor(HPR)using Lactobacillus plantarum under aerobic conditions employing lactose(40 g·L-1)as a carbon source,and a second reactor for the oxidation of ferrous iron by two main pathways:the oxidation with H2O2(feeding from the first reactor)and by the bacterial strain Acidithiobacillus ferrooxidans.The HPR was modeled using the following approach.

Biomass reaction rate:

Lactate reaction rate:

The mass balances for each reactant and product for the HPR are given by Eqs.(3)-(7).

Lactose mass balance:

Biomass mass balance:

Lactate mass balance:

Hydrogen peroxide mass balance for HPR:

Oxygen mass balance:

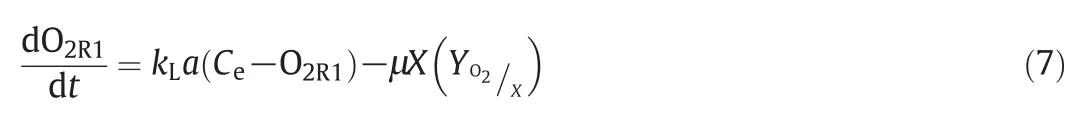
where Ce,is the saturation concentration of oxygen in water at 30°C,O2R1is the concentration of oxygen in the bulk in the HPR at time t,with kLa=15 h-1[17].A perfectly mixed system was assumed.It is important to remark that in biphasic and multiphase systems,which are common for most bioprocesses,a correction factor is commonly considered in the mass balance equation[18],which is defined as the ratio of the mass transfer coefficient with chemical reaction to that without reaction.In the case of oxygen,this consideration may be neglected due to experimental evidence of enhancement factors for microbial culture broths only slightly or negligibly larger than 1,owing to low bio-reaction rate[19].Therefore,the enhancement factor may be disregarded from the equation.

Fig.1.Schematic representation of the modeled SBR-type system for ferrous iron oxidation,which consist of two batch reactors,the first is used for hydrogen peroxide production and the second one for the ferrous oxidation process.

During the operation of the iron oxidation reactor(IOR),the oxidation is realized by both hydrogen peroxide and its product decomposition(HO·)as follows:

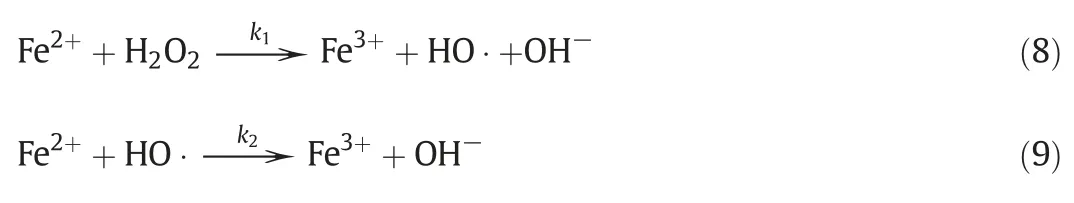
Notwithstanding,oxidation by soluble oxygen was also considered since dissolved oxygen is present in the aqueous phase,according to the following balanced reaction:

Moreover,in the IOR,the oxidation is accomplished by bacterial oxidation(Acidithiobacillus ferrooxidans).The stoichiometric balanced reaction for the biological oxidation is given by

The reaction rates for Eqs.(8)-(11)are given by:

The mass balances for each reactant and product for the IOR are given by Eqs.(16)-(21).

Fe2+mass balance:

Fe3+mass balance:

Oxygen mass balance:

where Ce,is the saturation concentration of oxygen in water at 30°C,O2R2is the concentration of oxygen in the bulk in the IOP at time t,with kLa=15 h-1[17].

Hydrogen peroxide mass balance for the IOR:

HO·mass balance:

H+mass balance:

The model is composed by 6 kinetic rates[Eqs.(1)-(2),Eqs.(12)-(15)]and eleven differential equations[Eqs.(3)-(7),Eqs.(16)-(21)]describing the corresponding mass balances.The model describes the production of H2O2using the aerobic metabolism of Lactobacillus species which could eliminate the dissolved oxygen in the medium by producing H2O2[8,16].The H2O2produced is fed to a second reactor(IOR)where the oxidation is carried out slowly by this oxidant agent at pH=2.This process may be enhanced by the addition of Acidithiobacillus ferrooxidans in the medium culture,which can be grown under acidic conditions and is able to oxidize Fe2+using its enzymatic complex[20,21].Reaction rates constants(k)taken from the literature were used as the starting point for parametric adjustment[22-24].It is important to remark that all simulations were done considering only the single set of parameters and avoiding a re-identification of the model parameters against any of the different experimental campaigns,which allows specifying the practical limitations of the proposed model structure,providing a more complete scope for the decision-making process.

2.2.Sensitivity analysis and bifurcation analysis

Simulations were performed in the Simulink tool of MATLAB®(R2017a).Simulink simulates the production of H2O2and the oxidation of ferrous iron in terms of interconnected block diagrams and sends the output to MATLAB for further analysis.The simulations were performed with the ode4-Runge-Kutta solver of Simulink with a fixed-size of 0.01.The parameter estimation was realized using the Levenberg-Marquardt algorithm of the parameter estimation tool of Simulink.

For our study case,a global sensitivity analysis was performed in the sensitivity analysis tool of Simulink to determine the highly influential parameters of the proposed model.This methodology generates random parameter values in a specified range considering a probability distribution(continuous uniform distribution)and also evaluates the cost function(Signal Matching requirement)at each sample point.Parameters with low influence have a negligible effect on the model predictions,while the most influential parameters require a greater certainty to increase the robustness of the model[25].Besides,to characterize the final state behaviour of the system operating under a batch regime,bifurcation diagrams were elaborated considering the most influential parameters(resulting from the sensitivity analysis),namely,the volumetric mass transfer rate(kLa),the saturation concentration of oxygen in the bulk(Ce),the specific maximum growth rate(μmax),the power parameters n,α and ζ,and the reaction rate constants(k1,k3)as bifurcation parameters using Simulink,which works within the framework of MATLAB.

3.Results and Discussion

3.1.Model validation

The predictive capacity of the proposed kinetic model for the H2O2reactor(HPR)was assessed by comparing the experimental data for three different initial conditions of the culture with the model predictions.For modeling the HPR,an unstructured phenomenological kinetic model was used,since these models aim to find a midpoint between complexity and practicality to create a structure that considers as many substrates and products involved in the metabolic system as possible.This in turn,could lead to the development of better predictive kinetic models applicable to a wide range of peer processes.Table 1 presents all the kinetic parameters obtained from the parametricadjustment,considering the experimental data reported by Fu&Mathews[16],regarding the following initial conditions:Xi=0.05 g·L-1,Laci=40 g·L-1,Lati=0.3 g·L-1,H2O2i=0 g·L-1and O2R1i=0.008 g·L-1,obtaining correlation coefficients(r2)of 0.98,for biomass and lactose,and r2=0.99 for lactate with p-value＜0.001,which ensures that there is no significant difference between the experimental data and the predicted values(Fig.2).Hydrogen peroxide production was simulated using an H2O2-Biomass yield=0.0041 g H2O2·(g Biomass)-1),which agrees with the value reported by Marty-Teysset et al.[8].

Table 1 Kinetic parameter values for modeling the HPR and IOR

The key kinetic parameters,such as the maximum specific growth rate(μmax),affinity(KsLac)and inhibition constants(KiLac)for lactose,as well as inhibition constants for lactate(KiLat)were within the values reported for this kind of process,which may depend on the initial culture conditions[2,16].The set of parameter values adjusted as described above were used to evaluate the predictive capacity of the model to describe different scenarios.Culture conditions using lactose concentrations(20 and 50 g·L-1),with different Lactobacillus strains,as well as different temperature and agitation rates were evaluated by modeling the dynamical behaviour[2,8].Fig.3 shows that the predicted values obtained by the model fit the experimental data at the final state for lactose,biomass,H2O2,lactate and pH,for the above-mentioned conditions.It is also important to remark that differences between experimental and predicted data can be attributed firstly to the nonlinear nature of biological systems,and secondly to the changes in the biochemical environment and regulatory mechanisms that are not considered in the model[11].

The iron oxidation reactor(IOR)was modeled considering a phenomenological structured kinetic model,which was constructed using a power law approach since these mathematical structures are widely used to describe the kinetics of biochemical systems and mineral processes[26].The parametric adjustment was performed with the experimental data reported by Ma&Lin[10],considering the following initial conditions:Fe2+i=0.558 g L-1,O2R2i=0.008 g·L-1,H2O2i=0.0102 g·L-1(300 μmol·L-1)and pH=2,obtaining a correlation coefficient r2=0.99 for the Fe2+state variable(Fig.4).It is important to note that little information is available regarding the modeling of the variables involved in bioreaction systems that consider both the chemical and biological oxidation properties[10],which may lead to uncertainties in the model predictions.Therefore,kinetic parameters such as the reaction rate constants(k1,k3,k3and k4)were ensured to be within the range observed in literature[22-24],to obtain suitable predictions of oxygen,ferrous iron,H2O2and pH,which present a consistent trend of the microbial and chemical oxidation of Fe2+[5,27].Once the predictive ability of the model was assessed,different initial concentrations of ferrous iron were evaluated using the single set of identified parameters.The initial conditions consist of 0.558 g·L-1and 0.0558 g·L-1ferrous iron,and:0.0034(100 μmol·L-1)and 00.034(1000 μmol·L-1)g·L-1of H2O2,respectively[10].A correlation coefficient of r2=0.98 was observed under these conditions.As shown in Fig.5 the model can simulate the oxidation of ferrous iron and can predict other variables of interest that are not considered frequently.These variables can offer a wider panorama of the process behaviour.It should be mentioned that although there is a lack of experimental data about these systems that cover the measurements of a greater number of variables,therefore,the stoichiometry was maintained,and the predictions were observed to be in the proper order of magnitude.

Fig.2.Parametric adjustment by simulation and experimental data reported by Fu&Mathews[16]using Lactobacillus plantarum to produce H2O2using an initial lactose concentration of 40 g·L-1 under aerobic conditions.

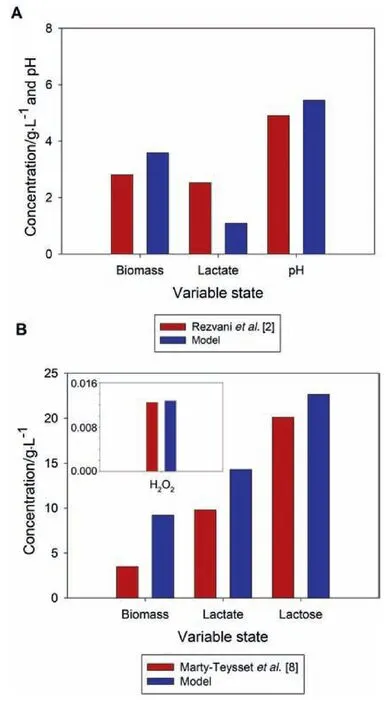
Fig.3.Evaluation of the predictive capacity of the proposed kinetic model by observing the final states of the variables of interest at 7 h and 52 h under aerobic conditions.A)Simulation and experimental data using Lactobacillus delbrueckii subs.Bulgaricus at initial lactose concentration of 20 g·L-1,B)simulation and experimental data using Lactobacillus fermentum and an initial lactose concentration of 50 g·L-1.

From Figs.4,5 a rapid consumption of H2O2is observed,as well as oxygen at the beginning of the kinetics.These effects are due to the high reaction rate constants for Fenton's reaction[Eq.(8)]and the utilization of dissolved oxygen by microorganisms as electron acceptor[Eq.(11)][1].From Figs.4,5 it can be observed a rapid increase of the oxygen concentration in a small-time interval that can be explained by the reactive oxygen species(ROS)produced from the Fe2+oxidation by H2O2and O2,such as,superoxide,hydroxyl or hydroperoxyl radicals,which may react with each other or with Fe3+to form O2[27,28].With the results displayed in Figs.4 and 5 it can be inferred that at low Fe2+/H2O2ratios a fast oxidation process is carried out.Moreover,using high Fe2+concentrations up to 0.558 g·L-1the oxidation is almost completed at 20 h at both molar ratios of 33(Fig.4)and 99[Fig.5-(A2)],which implies that when the H2O2is exhausted the microbial iron oxidation continues,by dissolved oxygen and the produced reactive oxygen species.Note that this process is accomplished under acidic conditions(pH=2)and simulations show that this value is maintained almost constant through the kinetics,a trend that is consistent with the range reported for oxidation of iron by microorganisms[6].Figs.4,5 also show that pH remains constant during the chemical-biological iron oxidation and may be related to the simultaneous microbial oxidation and the hydrogen protons released from the chemical interaction of ROS.Our results agree with the experimental observations of Okibe et al.[29],who reported that pH remains unchanged during the microbial iron oxidation under low and high Fe2+concentrations.Although the specific growth rate and the number of cells may be modified by the initial Fe2+concentration,our results showed only a diminishing of the reaction time since a small difference of initial concentrations were evaluated,and similar microbial growth can be obtained at concentrations in the range of 0 to 5 g Fe2+·L-1[30].In this study,the biomass growth was not considered in the modeling since the microorganisms were only considered as a catalyzer for the reaction and the biomass growth does not present important changes when the H2O2concentration increases[10].

3.2.Parametric sensitivity analysis

Having identified the parameters that present the best model fitting,a global sensitivity analysis was conducted,which allows determining the most influential parameters of the HPR model(Fig.6).In modeling tasks,robustness can be defined as a property that allows a mathematical structure to maintain its validity despite internal or external perturbations.One of the tools to describe the robustness of a mathematical model of a complex biological system is sensitivity analysis,which aims to determine which of the parameters have the most/least sensitivity when perturbed or are most subject to uncertainty,or to errors in experimental parameter estimation.As expected,the model was highly sensitive to the cell growth rates(μmax),volumetric mass transfer(kLa),the equilibrium concentration of oxygen in the aqueous phase(Ce)and the power coefficient(n),which at the same time may be related to changes in the environmental conditions of the culture,such as temperature,initial substrate concentration,or pH[31,32].The sensitivity analysis for the IOR model(Fig.7)showed that the most influential parameters of the mathematical structure are power parameters such as α,θ and ζ,as well as the reaction rate constants k1and k3.This global analysis suggests that there is still a need for adjusting analytical/experimental or numerical techniques for the precise calculations of the kinetic parameters,in order to develop future studies of the process.For instance,a precise determination of the concentrations of Fe2+,HO·and O2should be made as far as possible,since these variables are related to influential power parameters(Greek-symbols).

Fig.4.Parametric adjustment of the ferrous iron oxidation using experimental data reported by Ma&Lin[10]using Acidithiobacillus ferroxidans as microbial catalyzer and 300 μmol·L-1 of H2O2(0.0102 g·L-1)under aerobic conditions with 0.558 g·L-1.

Fig.5.Model validation with experimental data obtained from Ma&Lin[10]with different initial concentrations of ferrous iron:0.0558(A1)and 0.558 g·L-1(A2)and hydrogen peroxide:0.034 g·L-1 and 0.0034 g·L-1,respectively.

Fig.6.Parametric sensitivity analysis for the hydrogen peroxide reactor model.

3.3.Bifurcation analysis

Fig.7.Parametric sensitivity analysis for the iron oxidation reactor model.

Our study employs an integrative analysis of the bioprocess,which consists of the construction of a kinetic model with a high predictive capacity,based on the comparison of experimental data and simulations.Afterwards,the more influential kinetic parameters were determined by conducting a global sensitivity analysis.The information provided by this analysis was used to carry out a bifurcation analysis.In this way,our approach suggests the use of both complementary kinetic-parameter analysis as a useful methodology to provide a wider view of the behaviour of the kinetic model parameters.On the one hand,a sensitivity analysis may offer information about the most influential parameters,and on the other hand,the bifurcation diagrams of these parameters can display the ranges of the parameters where there is a greater influence,and the effect of the change of these parameters on the state variables.This information is useful to know the limitations of the predictive capacity of the proposed mathematical structure of a given process[33,34].Bifurcation analysis was used to construct the curve traced for the final states of the different variables of importance in the process for the HPR and IOR,employing the most influential parameters described above as bifurcation parameters.

The HPR analysis was carried out with the initial conditions reported by Fu and Mathews[16],consisting of(g·L-1):Xi=0.05,Laci=40,Lati=0.3,H2O2i=0 and O2R1i=0.008.For the HPR,the parameters μmax,kLa,n and Cewere used as bifurcation parameters(Fig.6)in the MATCONT software package.Fig.8 shows the bifurcation diagrams obtained for the HPR.Fig.8(A1)and(B1)shows that changes of the parameters μmaxand Cebetween 0.29-0.90 h-1and 0.005-0.0078 g·L-1,respectively,may modify drastically the model predictions of biomass and H2O2.An increase of the equilibrium concentration of oxygen in water as well as an increase of μmaxlead to a higher biomass and H2O2production at the end of the culture.This fact may be explained by considering that high biomass concentrations may reduce chemically higher amounts of oxygen to increase the H2O2production.In the same way,marked changes of the same state variables are observed by modifying the parameters kLa and n in the ranges of 16-24 h-1and 2.21-2.37(dimensionless),respectively[Fig.8(A2)and(B2)].The decrease of n as well as an increase of kLa lead to decrease both biomass and H2O2concentrations.The increase of kLa is commonly related to an increase of agitation.A more turbulent flow coupled to an increase of the dissolved oxygen in the bulk may diminish the microbial growth,since oxygen is considered toxic for Lactobacillus strains[8],which in turn may decrease the production of H2O2.

For the IOR,the parameters α,ζ and the reaction rate constants k1and k3were used as bifurcation parameters(Fig.7).The IOR bifurcation analysis was performed considering the initial concentrations(g·L-1):Fe2+=0.0558,O2R2=0.008,H2O2=0.034(1000 μmol·L-1)and pH=2[10].Fig.9 displays the bifurcation diagrams for the IOR.This figure display that by modifying the α and ζ parameters in the range of 1.24-4.57 and 1.71-5.14,respectively,significant changes are observed in the final Fe2+concentration.In this way,the same range of parameters does not present marked changes in the final pH.Moreover,regarding k1and k3,ranges of 10-845(L·g-1·h-1)and 0.0001-0.021 h-1respectively,may modify the predicted final Fe2+concentration within the limits of 8.09×10-9-0.051 g·L-1.For the case of oxygen,changes of k1between 10 and 545(L·g-1·h-1),and k3from 0.001 h-1to 0.03 h-1,may lead to a final oxygen concentration in the range of 0.007-0.008 g·L-1.All these results lead us to consider that incorrectly measured concentrations of Fe2+,as well as incorrect determinations of the reaction rate constants,may lead to incorrectly modeled and simulated data[11].

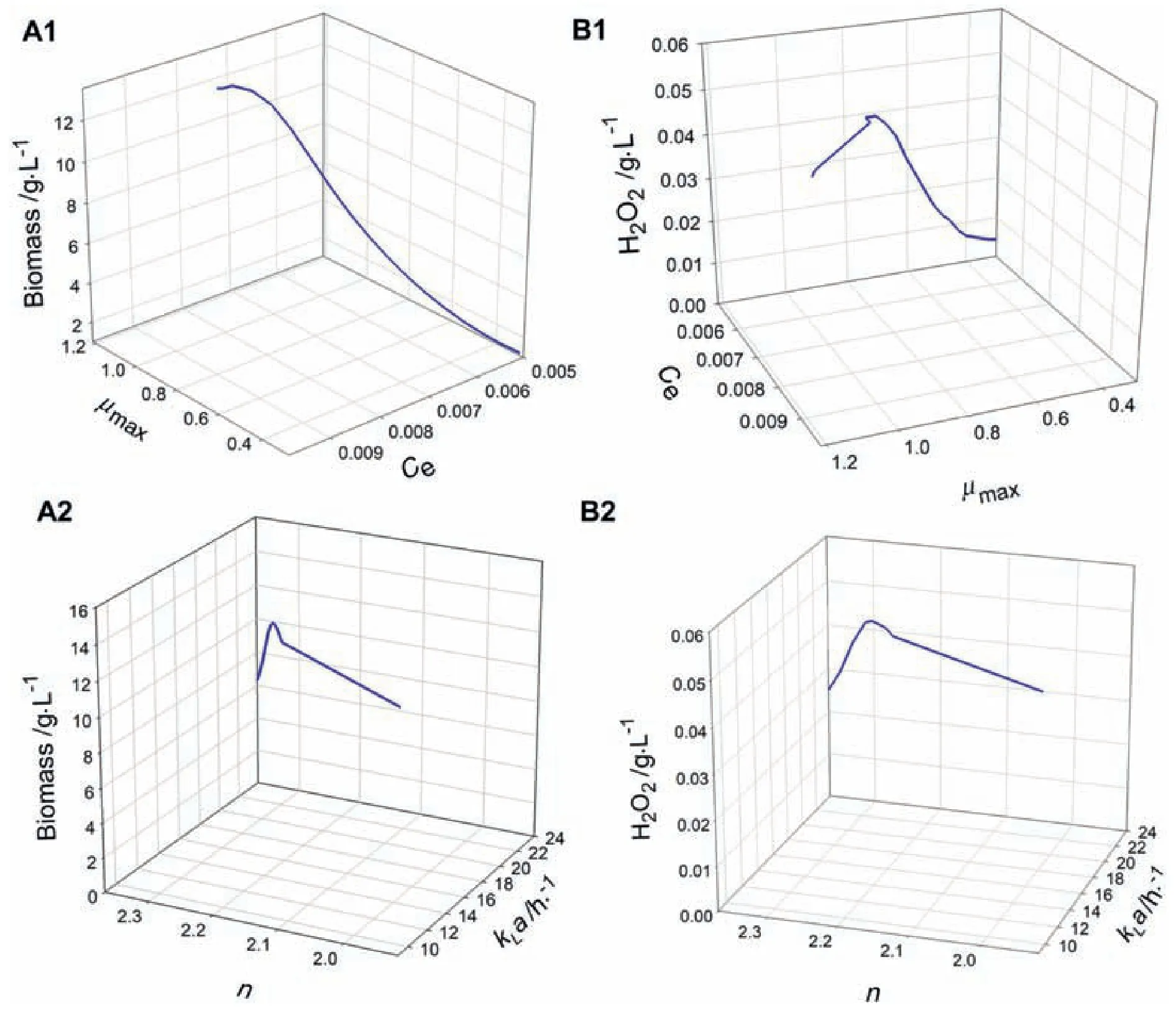
Fig.8.Bifurcation diagrams for the HPR,considering μmax,kLa,n and Ceas bifurcation parameters,for final concentrations of biomass and H2O2.

Fig.9.Bifurcation diagrams for the IOR,considering k1,k3,α and ζ as bifurcation parameters,for final concentrations of ferrous iron,pH and dissolved oxygen.

The development of predictive mathematical models commonly requires the estimation of parameter values from experimental data,which suffer from different levels of uncertainty[14,34].To obtain a higher degree of certainty of the model,tools such as sensitivity and identifiability may be complemented with a bifurcation analysis to obtain a more complete view of the influence of the kinetic parameters on model predictions of the process.

4.Conclusions

Our study proposes that an SBR-type system can be used as a useful technology for ferrous iron oxidation in aqueous phase.Moreover,we present a simple and practical procedure to carry out a parametric analysis that provides a more complete panorama of the kinetic influence of the model parameters.This approach includes the development of a mathematical kinetic model,which considers the use of iron oxidizing and hydrogen peroxide producing bacteria,the chemical oxidation via H2O2and the dissolved oxygen;a sensitivity analysis,and finally,a bifurcation analysis of the model parameters.The sensitivity analysis allowed demonstrating that the most influential kinetic parameters for both HPR and IOR models were the reaction rate constants,kLa,the saturation concentration of oxygen(Ce),the power n,as well as the parameters α,β and ζ.The bifurcation analysis presented the limits where those parameters have a greater effect on the simulated state variables of interest.

Nomenclature

Cesaturation concentration of oxygen,g·L-1

HPR hydrogen peroxide reactor

IOR iron oxidation reactor

KiLacinhibition constant for lactose,g·L-1

KiLatinhibition constant for lactate,g·L-1

KsLacaffinity constant for lactose,g·L-1

k reaction rate constant,h-1

kLa volumetric mass transfer coefficient,h-1

Lac lactose concentration,g·L-1

Lat lactate concentration,g·L-1

n power parameter

O2R1oxygen concentration in the aqueous phase in the HPR,g·L-1

O2R2oxygen concentration in the aqueous phase in the IOR,g·L-1

rmaxLatspecific maximum growth rate,h-1

YX/Lacbiomass-lactose yield coefficient,g biomass·(g lactose)-1

μmaxspecific maximum growth rate,h-1

Acknowledgements

We acknowledge the National Council of Science and Technology(CONACYT)for the financial support via a postgraduate scholarship to E.N.Tec-Caamal,and with CINVESTAV-IPN for supplying the research facilities to perform this work.