Change in internal energy of thermal diffusion stagnation point Maxwell nanofluid flow along with solar radiation and thermal conductivity

Mair Khan *,T.Salahuddin2,A.Tanveer2,M.Y.Malik,Arif Hussain

1 Department of Mathematics,Quaid-i-Azam University,Islamabad 44000,Pakistan

2 Department of Mathematics,Mirpur University of Science and Technology,Mirpur 10250,Pakistan

3 Department of Mathematics,College of Sciences,King Khalid University,Abha 61413,Saudi Arabia

Keywords:Maxwell nanofluid Viscous dissipation Solar radiation Variable viscosity Thermal conductivity Chemical reaction Stagnation point Shooting method

ABSTRACT This paper concerns the characteristics of heat and mass transfer in upper convected Maxwell fluid flow over a linear stretching sheet with solar radiation,viscous desperation and temperature based viscosity.After boundary layer approximation,the governing equations are achieved(namely Maxwell,upper convected material derivative,thermal and concentration diffusions).By using the self-similarity transformations the governing PDEs are converted into nonlinear ODEs and solved by RK-4 method in combination with Newton Raphson(shooting technique).The effects of developed parameters on velocity,temperature,concentration,fraction factor,heat and mass diffusions are exemplifeid through graphs and tabular form and are deliberated in detail.Numerical values of fraction factor,heat and mass transfer rates with several parameters are computed and examined.It is noticed that the temperature is more impactable for higher values of radiative heat transport,thermal conductivity and viscous dissipation.The comparison data for some limiting case are acquired and are originated to be in good agreement with previously published articles.

1.Introduction

The conjugate effects of heat and mass transfer are of particular importance in engineering and industry.Thermal diffusion and chemical species are major reasons for such development in industry and thus aids in many technological advancements for e.g.,underground energy transport,nuclear safety,production of polymers and ceramics,paper making,enhanced oil recovery,design equipment,food industry,fog formation to dispersion,temperature and moisture distribution in agricultural fields and so forth.Therefore the topic is of major interest among researchers in recent years.Bai et al.[1]discussed these effects on an upper convected material derivative over a stretching surface with convective boundary conditions.The viscoelastic fluid flow on a permeable sheet with heat and mass transfer aspects are analyzed by Zaho et al.[2].They executed the problem by implicit finite difference technique.The combined heat and mass transfer effects on a porous sheet with magnetic field is reported by Eid and Mahny[3].The Hall and Joule heating effects on peristaltic flow with heat and mass transfer are presented by Bhatti and Rashidi[4].Heat and mass transfer diffusions on nanofluid flow are analyzed by Jafarimoghaddam[5].Upadhay et al.[6]extended the work for Cattaneo-Christov heat and mass transfer for an unsteady Eyring Powell dusty nanofluid.Khan et al.[7]captured the effects for Williamson nonofluid yield by an inclined Lorentz force over a stretching surface whereas variable viscosity is considered to vary linearly with temperature.Gu et al.[8]numerically analyzed the heat and mass diffusions between air fluid and water surface.Khan et al.[9]examined thermal and concentration diffusions in Jeffery nanofluid approved by an inclined stretching sheet with Cattaeno-Christov model.Kandasamy et al.[10]investigated heat and mass transport on thermal and solutal stratifications induced of nanofluid flow over a vertical porous plate.The results clarify the temperature and concentration reduction with rise in thermal and solutal stratifications.

Chemical reaction involves rearrangement of the molecular or ionic structure of fluid or the conversion of one sort of chemically reacting species(reactants)to other species(product)is referred as chemical reaction.The effect occurs significantly in different branches of sciences and engineering.Chemical industry,energy transfer in cooling tower,cooling and power industry,drying of paper,flow in desert cooler,etc.are some examples.The chemical reaction characteristics up to first order are discussed by number of researchers in recent time.Rout et al.[11]presented the study on chemical reaction aspects on non-Newtonian fluid with transverse magnetic field corresponding to vertical plate.Narayana et al.[12]discussed the oscillatory flow with chemical reaction and heat transfer effects.Eid[13]combined the chemical reaction effect with two-phase nanofluid flow over a permeable surface.Kumar et al.[14]considered the rotating sheet and demonstrate the chemical reaction impact in a boundary layer flow with nanofluid.Khan et al.[15]explored the consequences of chemical reaction against MHD Carreau-Yasuda nanofluid over a stretching surface.Hayat et al.[16]addressed the heat and mass diffusions on second grade nanofluid flow over a rotating disk with chemical reaction and heat generation.Krishna et al.[17]illustrated the convective boundary layer flow on viscous fluid through permeable surface with influence of chemical reaction and heat source.

In recent years,the magnetic field with a flow stream of an electrically conducting fluid is found effective in thermal protection,nuclear reactors,purification processes,braking,propulsion and control,MHD generators,and pumps,flow meters and accelerators and in metallurgy.On the other hand the thermal radiation controls the excess heat generation and has many practical industrial applications.The amount of literature is available on study of magnetic field and thermal radiation now a days.Daniel et al.[18]illustrated the solar radiation heat transport in MHD nanofluid over a permeable stretching surface with combined chemical and viscous dissipation effects.Dogonchi and Ganji[19]examined the thermal radiation flow of heat transfer unsteady squeezing viscous fluid flow over a parallel plate surface along with Cattaneo-Christov heat diffusion model instead of classical Fourier's laws.Gupta et al.[20]explored the influence of thermal radiation in non-Newtonian fluid passed by inclined stretching surface.Wen et al.[21]discussed the MHD and radiation effects in Navier-Stoke equations and sort out the problem by collection specter method.Mishra et al.[22]examined the thermal energy phenomenon on stagnation point flow of nanofluid over a stretching surface.

Thus the aforementioned applications of various effects provide the main objective of this work.Particularly this paper models the heat and mass transfer aspects of non-Newtonian Maxwell nanofluid on a stretching surface.Stanation point and solar radiation effects are highlighted.The fluid viscosity and thermal conductivity are considered variable.The resulting system of mathematical expressions are simplified with an aid of suitable transformations.The appearing simplified system is then set to Shooting method for solution purpose.The numerical solutions are plotted in graphs and discussed in the last section physically.

2.Mathematical Formulation

Let us consider thermal radiation,thermal conductivity,viscous dissipation,chemical reaction on two dimensional laminar steady heat and mass transfer flow of an electrical conducting upper convected Maxwell nanofluid flow passed by a linear stretching surface placed in xdirection and y-axis is vertical to the sheet with stagnation point at the origin(as illustrated in Fig.1).It is suppose that the sheet is stretching with linear velocity u=Uw(x)=cx and the free stream velocity u=ue(x)=ax,here a and c are the positive constant.The temperature at the surface is conserved at Twand T∞for away from the plate,and same assumption for nanoparticle volume fraction Cwand C∞.An external magnetic field H0normal to the stretching sheet is applied.

Fig.1.Schematic of the problem.

Form the above basic assumptions,the required governing equations are as follows:

due to hydrostatic and magnetic pressure gradient the force will be in equilibrium as given by

Hence,Eq.(2)becomes

now energy and concentration equations are

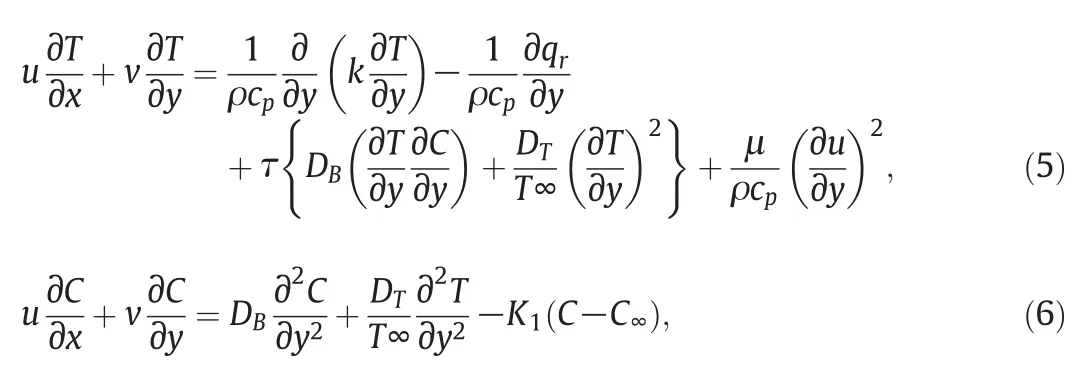
the boundary condition are given as

The temperature based viscosity(see Ref.[23])is

temperature based thermal conductivity is given as

where qris the radiative heat flux,utilizing the Rosseland approximation for radiation(see Ref.[19]),we get

expressing T4by utilizing Taylor's series term about T∞and neglecting higher order terms

using Eqs.(10)and(11)

here,μ0is the fluid viscosity,Fsis the inertial factor,K∗is the permeability,K1is the rate of chemical reaction,m is the variation viscosity,k∘is the absorption constant,α∘is the Setfan-Boltzman constant,(u,v)are the velocity components along the(x,y)directions,ρ is the density,μeis the magnetic permeability velocity,σ is the electrical conductivity,λ is the Maxwell fluid parameter,ν is the kinematic viscosity,k is represents thermal conductivity,DBis the Brownian motion,τ=is the ratio of nanoparticle heat capacity and base fluid thermal capacity,αf=represents the thermal diffusion,Tw(x,y)is known as the temperature at the wall,Cw(x,y)is known as the concentration at the wall,T and C are the temperature and concentration fluid respectively,Cpis the specific heat,T∞and C∞are the temperature and concentration free stream.Temperature of the sheet Tw=T∞+bx,for heated surface b＞0 so Tw＞T∞and for cooled surface b＜0 and Tw＜T,b is a constant and DTis known as the thermophoresis diffusivity.

The similarity variables gives the dimensionless quantities

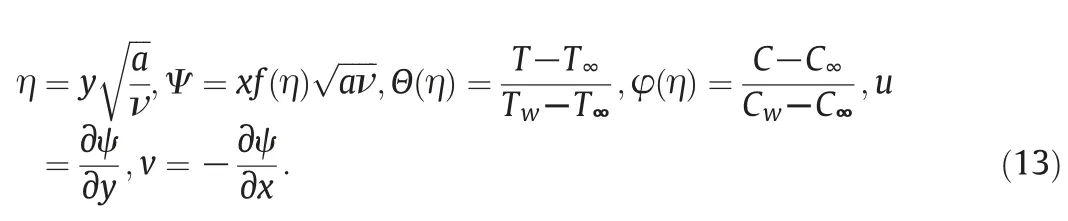
Incompressibility condition(1)is automatically satisfied and Eqs.(4)-(6)take the following nonlinear differential form

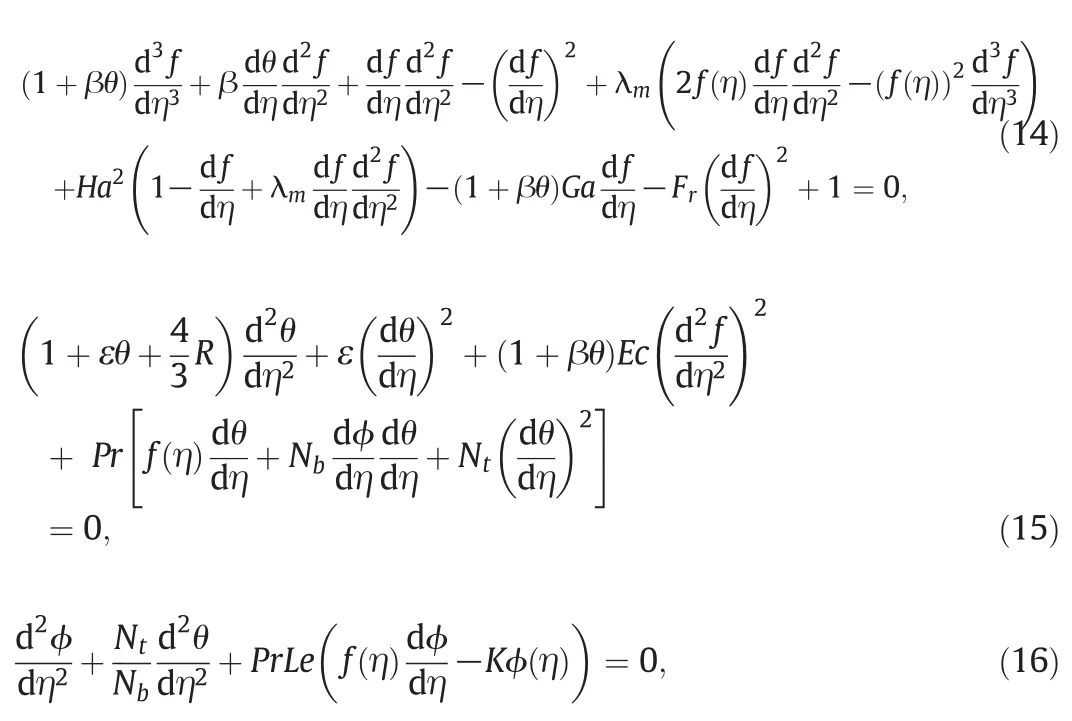
using Eq.(12),the associated boundary conditions become

Friction factor coefficient(Cf)is defined as:

here τwdenotes the wall shear stress is given as:

The Nusselt number is defined as:

The mass transfer rate is defined as:

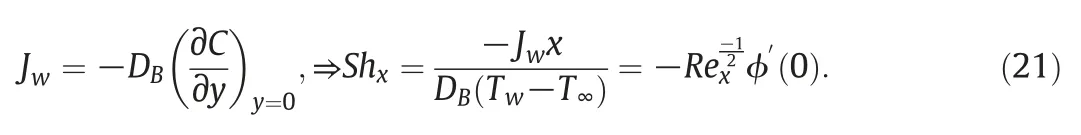
3.Numerical Procedure

Nonlinear differential Eqs.(14)-(16)with boundary condition(17)are preserved by a convenient Runge-Kutta based shooting technique.Among some other numerical method,shooting method(Cash and karp)is more flexible for the aim that the initial guesses control the convergent criteria.The main steps are as follows:

1.Reduce differential Eqs.(14)-(16)into a system of fist order differential form.

2.Insert the three unknown initial approximation.

3.Finally,solved the converted system of 1st order equations by Runge-Kutta based shooting scheme.

4.The unfamiliar unknown initial condition have been approximated with Newton's method in such a way that the residuals are less than error i.e.10-6.

5.The computational solution repeated until convergent criteria is satisfied.

4.Results and Discussion

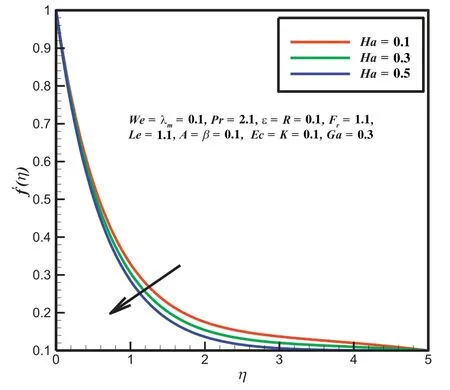
Fig.2.Outcome Ha on f′(η).

Fig.3.Outcome Ga on f′(η).

Fig.4.Outcome Fron f′(η).

In the current section,the governing physical parameters and numerical results are illustrated through Figs.2-17 and Tables 1-5.Figs.2-6 describe the physical behavior of non dimesnional-dimensional velocity subject to Hartmann number,porosity parameter,inertia factor,fluid relaxation parameter and temperature based fluid viscosity parameter.In Fig.2 represents the velocity profile for several values of Hartman number Ha.It is analyzed form this figure that enhancing values of Hartmann number Ha decelerates the velocity profile.This reduce behavior indicates that the transverse magnetic field in interaction by electric conducting fluid develops resistive force so called Lorentz force.Fig.3 illustrates the influence on velocity graph for various values of porosity parameter Ga.It seen that the rising values of porosity parameter Ga declines the velocity profile.Because the permeability enhances the resistance of the permeable sheet which tends to decrease the velocity profile.Fig.4 illustrates the variation in inertia factor Fron velocity profile.It is obvious that improve in values of Frsorts a resistive force which decelerates the velocity plot.Fig.5 describes the variation on velocity profile for corresponding values of fluid relaxation parameter λm.It is clear form this figure that the momentum boundary layer thickness reduces by increasing the fluid relaxation parameter λm,and consequently induces an intensifications in the absolute values of the velocity profile at the surface.Fig.6 examines the effect of temperature based fluid viscosity β on velocity profile.It can be analyzed that the velocity profile enhances by enhancing the temperature based fluid viscosity parameter β.

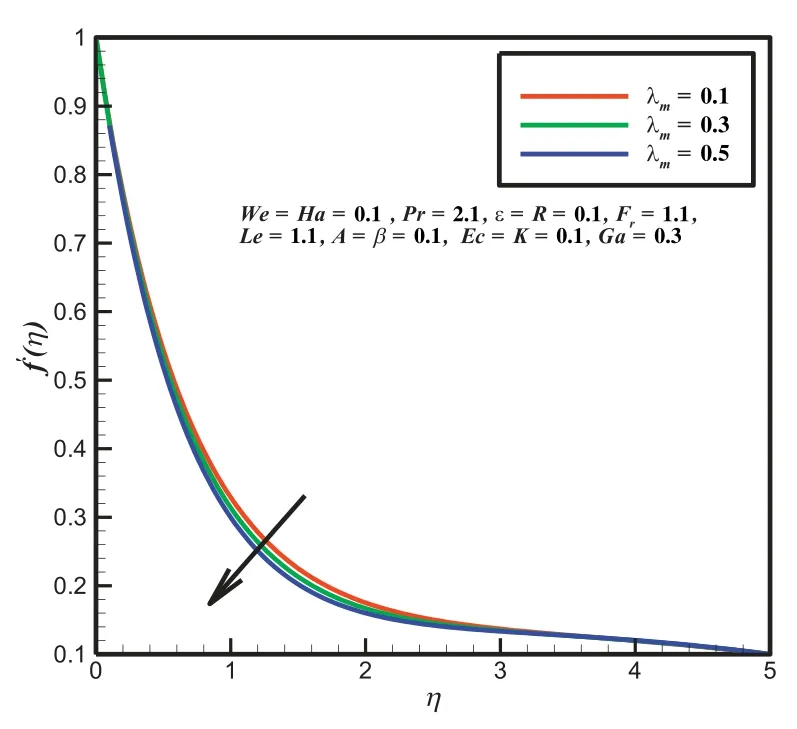
Fig.5.Outcome λmon f′(η).

Fig.6.Outcome β on f′(η).

Fig.7.Outcome Pr on θ(η).

Fig.10.Outcome Ec on θ(η).

Fig.11.Outcome R on θ(η).

Fig.12.Outcome R on θ(η).

Fig.13.Outcome Le on ϕ(η).

Fig.14.Outcome K on ϕ(η).

Fig.15.Outcome of β and Ha

The disparity in temperature distribution with reference to similarity variables such as Prandtl number,Brownian motion factor,thermophoresis constraint,thermal radiation parameter,Eckert number and small parameter are presented in Figs.(7-12).It is perceived that Fig.7 represents the temperature distribution for corresponding values of Pr.By enhancing the values of Pr reduces the temperature profile and also reduces thermal boundary layer thickness.It is fact that the rising values of Pr corresponding to the moderate's thermal diffusivity and decelerates the boundary layer thickness.Fig.8 illustrates the deviation on temperature for different values of Nb.It can be investigated as Nbenhances the mass diffusivity rises which leads to increase the temperature profile in the boundary layer segment.Fig.9 shows the variation of Nton temperature profile.It is found that for improved values of Nttemperature distribution also top ups.Because increase values of Nt,generates the rise in the thermophoresis force which have trend to move nanomaterials form hot surface to the clump surface.Fig.10 establishes the effects of Eckert number Ec on temperature profile.It is clear that the kinetic motion increases by increasing over the energy enthalpy which enhances the temperature profile.Fig.11 displays the influence of thermal radiation R on temperature distribution.It seen that the temperature profile rises due to fact that the conduction effects of the nanoliquid enhances in the occurrence of thermal radiation R.Therefore for large values of radiation parameter R means more heated surface,so enhances the heat transfer rate within boundary layer region.It is also clear that the thermal boundary layer rises by rising the values of radiation parameter R.Fig.12 examines the influence of small parameter ε on temperature distribution.It is also noticed that enhance in small parameter ε corresponding to improve the kinetic energy of the fluid materials which enhances variation of thermal characteristics.

To explore the behavior of nanoparticles concentration against Lewis number and chemical reaction are discussed in Figs.13-14.It is apparent that Fig.13 scrutinizes the influence of Lewis number Le on concentration profile.It can be examined that the concentration profile reduces significantly for developing values of Lewis number Le.Fig.14 reveals the influence of chemical reactive spices K on concentration profile.It seen that for extensive values of K,concentration profile reduces.

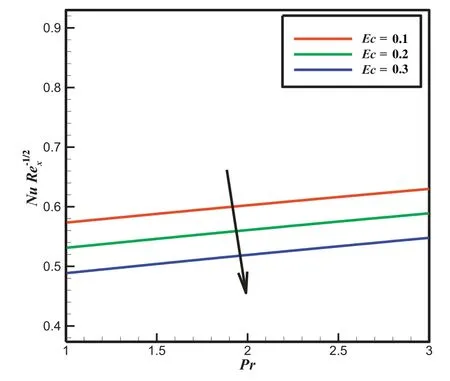
Fig.16.Outcome of Ec and Pr

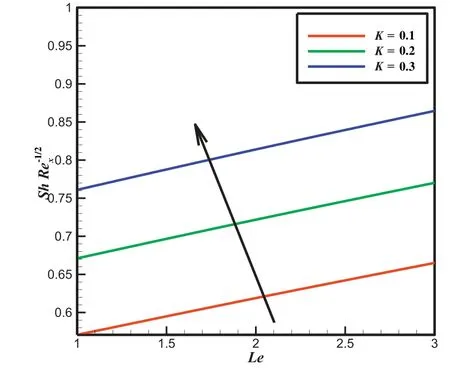
Fig.17.Outcome of K and Le

Figs.15 and 16 show the skin friction coefficient and heat transfer rate for different values of variable viscosity parameter β and Eckert number Ec with HaPr and Pr.It is clear that the reduction in friction factor and heat transfer rate is noticed for enhanced values of β and Ec.Fig.17 represents the nature of mass transfer rate for several values of chemical reaction K with along Le.It is found that the mass transfer rate increases for increasing values of chemical reaction K.

Tables 1 and 2 demonstrate the deviation for several physical parameters on friction factorand heat transfer rate NuIt is found that reduction is noticed for rising values of variable viscosity parameter β,inertia factor Fr,porosity parameter Ga,Eckert number Ec and thermophoresis parameter Nband increase is noticed for Ha and Pr.Table 3 designates the numerical results on the mass transfer rate Shfor several physical parameter.It can be analyzed that the mass transfer rate Shis enhancing function for increasing parameters Le,K and Nb.For the justification of current numerical scheme,the results are presented and examined with Afify and Elgazery[25]in a limiting case for Ec=R=ε=Ga=FR=0.1,NPrb=0.1,Nt=0.5,and Pr=Le=1.0.The numerical result shows good agreement as demonstrated in Table 4.Further the numerical outcomes are also compared with Khan and Pop[24]and Khan et al.[9]in Table 5.

5.Conclusions

The current article presents the stagnation point,viscous dissipation,solar radiation,variable thermal conductivity and chemical reaction on upper convected Maxwell nanofluid over stretching surface with Darcy Forchhemier effects.The Maxwell fluid,thermal and concentration equations are simplified by employing the self-similarity transformations.The governing differential equations are solved with help of RK-4 based shooting technique.The main concluding results are summarized as below:

·Due to the increase in variable viscosity β and fluid relaxation parameter λm,the velocity profile enhances.

·An intensification in the Hartmann number Ha,porosity parameter Ga and inertia factor Fris noticed.

·Increase in Prandtl number Pr reduces the temperature profile.

·Temperature profile increases by increasing the values of Eckert number Ec,radiation parameter R,Brownian motion Nb,thermal conductivity parameter ε and thermophoresis parameter Nt.

·Concentration profiles reduces for increasing values of chemical reactive species K and Lewis number Le.

·For lager values of variable viscosity parameter β and Eckert number Ec the friction factor and heat transfer rate reduces.But the opposite behavior is noticed in mass transfer rate.

Table 1 Numerical results of(1+βθ(0))f''(0)(1+λm)for different values of Ha,β,Frand Ga when λm=0.1,Nt=0.5,Nb=Ec=ε=K=0.1,Pr=2.1 and Le=1.5

Table 2 Computational results of-（1+ R）θ′（0）for unlike values of Pr,Ec,and Ntwhen λm=Nb=Ec=Ha=ε=Ga=K=Fr=0.1，β=0.9 and Le=1.1

Table 2 Computational results of-（1+ R）θ′（0）for unlike values of Pr,Ec,and Ntwhen λm=Nb=Ec=Ha=ε=Ga=K=Fr=0.1，β=0.9 and Le=1.1

Table 3 Numerical results of—φ′(0)for corresponding values of Le,K and Nb

Acknowledgement

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University,Abha 61413,Saudi Arabia for funding this work through research groups program under grant number R.G.P-59/40.

Table 4 Comparison of the friction factor Cffor various values λmand Ha when Nb=0.1 and other all parameter zero

Table 4 Comparison of the friction factor Cffor various values λmand Ha when Nb=0.1 and other all parameter zero

Table 5 Numerical comparison of heat transfer rate—θ′(0)and mass transfer rate—φ′(0)when Pr=10,Nb=0.1 and other all parameters zero