高中数学提升学生思维空间的思考和探究

张九州

浙江省杭州市临安区於潜中学 浙江 杭州 311300

1 问题发散性

思维的聚合与发散是两个不可分割的可逆的有机整体，大多数情况学生乐于聚合，寻找答案，聚合成唯一，这是一种习惯性思维，但发散性则相对薄弱，对这方面的思维进行训练，乐于给学生做充分思考，并对想法作一个综合性的汇总，有利于提升思维的立体空间

案例2、人教版选修2-3计数原理P5页例4

要从甲、乙、丙3幅不同的画中选出2幅，分别挂在左、右两边墙上的指定位置，共有多少种不同的挂法?

(先独立做)发现一个学生，立马请他回答

学生1：分三步，甲有2个位置，同样乙、丙，共2×2×2＝8。

学生2：题目要求是选出两幅挂出去就可以了，而他把三幅都挂出去了

学生3：分两步，先从3幅中选1幅挂在左，再从剩下的两幅中选出1幅挂在右就好了3×2＝6种

学生4拿着他的解法站起来，老师我的式子也是3×2，但想法不一样的，不知道对不对?

学生5：前两位同学的3×2其实可以归结为映射问题，即把左右两幅画的位置作为集合A，把甲乙丙三幅画看成集合B，即是从A到B的单映射有几个。

学生6：分成三类，第一类，选出甲乙，挂出有2种，第二类选出乙丙，第三类甲丙同理，共2+2+2＝6

反思1：虽然这些想法很多，发散思维很丰富，但却始终围绕了计数原理中的分类分步原则，树立了“形散而神不散”的风格。

反思2：从这个问题的背景来说再简单不过了，之前学生也很不以为然，但是针对这个问题的发散后，改变了大多数同学看书本的态度，体现了“小问题，大思维”，“源于教材而高于教材”，变“教课本为用课本教”的理念，效果非常好，比讲3个难题还要好，我想这归功于还空间给学生，还主动给学生，因为有一位名家说过“学生的创造力是惊人的”，如果你给他一片云，他可能会还你一片天空。希望我们的学生能在广袤的思维空间中自由翱翔。

2 问题质疑性

目前的教学现状是追求问题的准确性和最优化，但很少对教材，思路，解法进行批判式的精神，这是不利的。在学习时变“接纳式学习“为”批判式质疑“，无疑是可以提高学生认识事物的辩证思维空间

案例3、选修2-3，P59习题B1

甲、乙两选手比赛，假设每局比赛甲胜的概率为0.6，乙胜的概率为0.4，那么采用3局2胜制还是采用5局3胜制对甲更有利?你对局制长短的设置有何认识?

解：教参的标准答案是按照独立重复实验的方法，把甲赢的局数x看成对象，则P(x≥2)＝P(x＝2)+P(x＝3)＝0.620.4+0.63

但学生对于这个解法提出了质疑，

作业中的多数解法：令Ai表示第i次甲赢表示乙赢，

导向1：过右焦点F2和结论对换，即已知AB＝，求直线与x轴交

则P(A1A2)+PA2A3)+P(A1)＝0.62+2·0.4·0.66＝0.6286②

这符合生活常识，P(A1A2)即三局中先赢两盘的为胜者，不须打第三盘，

难道教参有问题吗?

答案也等于0.6286，两者是偶然的吗?他们是否有必然的联系?很多学生面对这个问题也是百思不得其解，(学生困惑的眼神)

照理①其中的P(x＝2)＝C230.620.4都是按打满三局来计算，是违背常理的。

课堂剖析；问题恰恰就出在两者的结构上，两相对比，就可看出其中端倪，②中的P(A1A2)是指即甲先赢两局，第三局可赢可输，包含了P(A1A2A3)和P(A1A2)两种情形，而P(A1A2A3)就等于①中的P(x＝3)，并且P(A1A2)与②另外的两者PA2A3)、PA2A3)合起来就是①中的P＝(x＝2)甲赢两局的情况，至此真相大白。(学生若有所思，有感悟)

①P(x＝2) P(x＝2)② P(A1A2A3)P(A1 A2A3)P(A1 A2A3) P(A1A2A3)

反思 两者解法存在答案的一致性并非是偶然的，标准答案就是按独立重复实验来书写的，但作为过程的解答来说前者更合理，更符合生活常识，两者之间有着必然的关联，但教参的解答显然不够自然，不符合生活实际，具有片面性，并不是最优解，可以摒弃。

3 问题导向性

案例4、人教版选修2-1圆锥曲线P60页例6

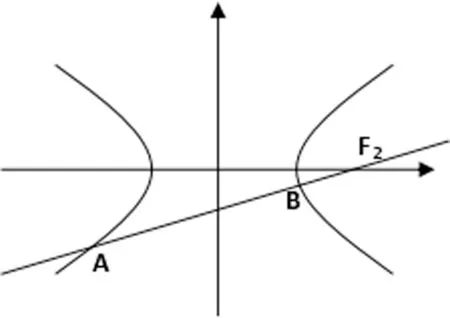
学生求解中，最后发现交点是(±3，0)两个答案

导向2：能否不通过计算，直接给出答案?

通过作图，学生很快发现斜率定，说明直线可以平行移动，恰好是过左、右两个焦点，如图(学生有点欣喜)

学生动手画图，发现直线可以绕右焦点旋转，要保证弦长不变，刚好是两条直线，并且对称，答案是两个正负根(学生很有成就感)

如图

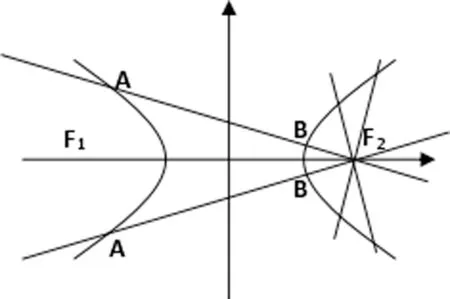
导向4：是不是真的两条，有没有漏的?和右支相交有没有考虑过?

(学生有点疑惑)继续思考

发现与右支相交是不可能的，原因在于在右支上的最短弦长仅为43＞

结束语

总结出的结论让学生充满兴趣和乐趣，课堂气氛更活跃了，学习的情趣更高了，学习的积极性更强了。