基于改进支持向量机模型的交通拥堵情况预测

辜丽琼 宋祖康 杨阳

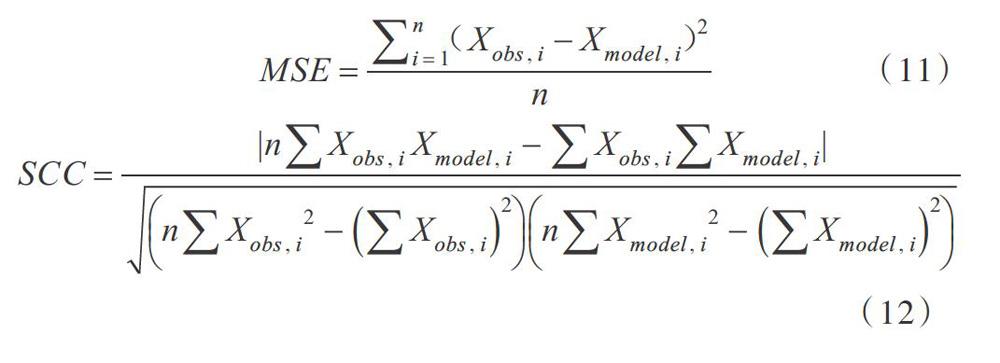
摘要：随着机动车数量的迅猛增加，城市交通拥堵状况日益严峻，城市道路拥堵严重影响着居民的日常工作和生活，因此研究道路拥堵程度，以及对道路拥堵变化进行预测则显得尤为重要。为此，构建一个基于拥堵指标的MM-SVR模型，在考虑下一时段可能到达路段的潜在车流量情况下，对道路拥堵情况进行深入探究。首先，融合速度、区域内交通流量构建道路拥堵程度指标，然后基于历史数据构建将马尔科夫链与支持向量机预测相结合的MM-SVR模型对道路拥堵进行预测，以向前"阶状态的交通流量和速度作为输入量，将道路拥堵程度指标作为输出量。在实例验证中，使用广州市某片区的实时交通流数据对模型效果进行评测，并且使用SVR以及Adaboosting模型进行对比实验。实验结果表明，该模型无论是在拟合優度还是预测误差上均优于对比模型，在实时反映交通流拥堵情况方面有着良好表现。

关键词：MM-SVR;时间序列;交通流;交通拥堵预测

DOI：10.11907/rjd k.191224

中图分类号：TP301 文献标识码：A 文章编号：1672-7800（2019）012-0061-04

0引言

如今，日益拥堵的交通已经严重影响到人们的工作与生活，因此如何改善交通问题，加快城市现代化建设已成为一个亟待解决的问题。作为大数据时代解决交通问题的重要手段，智能交通系统开始得到越来越多人的重视。在智能交通系统中，交通指标构建以及交通流的描述与预测是一个关键组成部分。如王妍颖等融合速度与车流量指标，构建北京拥堵指标体系，并对北京交通的真实情况进行指标分析;郑淑鉴等列举国内外交通拥堵评价指标计算方法，系统梳理了交通流指标现有研究成果，并对众多指标进行对比分析，搭建了一个比较完整的指标体系。在交通流预测方面的主要研究方向是短时间交通流预测，作为大密度、短间隔的时间序列，短时交通流具有非平稳与非线性特征。当前，对于交通流的预测方法主要有马尔科夫链、ARIMA、灰色系统与元胞自动机等传统模型，以及基于机器学习的SVM、Adaboosting等模型。其中，梁经韵等在经典单路段元胞自动机交通流模型基础上，将多个路段视为一个道路系统，发现拥堵路段与非拥堵路段之间存在明显界限的现象;唐毅等根据高速公路车流量数据，提出一种改进时间序列模型，克服了传统时间序列模型的不足;黄何列等针对常用聚类算法效果不理想的情况，提出一种新的交通流相似性度量准则——最大偏差相似性准则，并通过实验证明该算法明显优于常用聚类算法;傅贵等利用支持向量机回归理论对广州市交通流监测系统进行实验，实验结果的预测误差小于基于卡尔曼滤波的预测方法;王珂等提出一种基于灰色遗传支持向量机的短时交通流预测模型，首先运用灰色模型对交通流时间序列进行加工处理，以弱化噪声影响，之后通过支持向量机进行预测;康军等提出一种在线短时交通流预测方法，通过线性运算完成Lagrange乘子的更新，将在线LS-SVM模型的更新时间减少了约62.64%。以上研究证明了SVM模型在交通流预测方面的优良性能。

综上，大部分学者利用车流速度以及当前道路车流量研究道路拥堵情况，并取得了一定成果。但是交通流数据具有数量大、密度高且非平稳的特征，仅用传统时间序列理论进行计算，时间复杂度较高，而基于机器学习的拥堵情况预测研究，虽然改善了时间复杂度，但大都基于交通流这一基本面预测交通拥堵情况。在实际情况中，交通拥堵问题不仅取决于交通流大小，也与道路容纳力、车流速度以及每个时间段的潜在到达车流量有着密不可分的关系。因此，本文综合考虑区域内车流量与实时车流速度构建模型预测道路拥堵情况，结合该区域互联网道路评测情况，根据实时车流速度、车流量构建指标，充分考虑未来时间段有可能出现在道路中的潜在车流量，建立MM-SVR模型，并对所构建的拥堵指标进行模型训练，对下一时段的拥堵系数进行拟合预测，最后根据广州市某区域卡口与电警的真实数据验证模型的有效性。

1模型构建

1.1道路拥堵评价系数构建

鉴于道路拥堵程度不仅受通过该道路路段的实时交通流影响，而且还与该道路车流实际速度有关，比如不同道路等级的公路，在相同车流量的情况下，道路状况好的公路未出现拥堵，而道路状况较差的公路可能已处于拥堵状态。为了直观描述道路拥堵程度，本文融合速度与交通流量，对王妍颖等的研究进行改进。在王妍颖等的研究中，拥堵系数指标包含速度指标与车流量指标，其速度指标为：

首先构建H中的速度指标。本文数据包括深圳市局部地区道路的交通卡口监测数据、道路实时通行速度数据以及互联网导航平台数据。在道路路况表中，将该道路对应时段的行驶速度数据作为道路通行速度，对于某些时段数据的缺失，则用缺失时段前后5个滑口数据的平均数作为替代值。

依据上述数据构建道路路段速度指标，本文使用路段当日最大通行速度减去当时实际通行速度，再除以最大通行速度作为速度指标，具体如下：

其中，s表示该道路路段速度指标，Vmax表示在监测器上记录的通过该路段的最大通行速度，Vt表示监测器监测的该路段当前车流通行速度。

然后，构建路段的交通流量指标。利用统计的一天内某区域卡口的交通流量数据构建交通流量指标，以每2分钟为时间段对区域段交通流量进行统计。根据对区域交通流量的统计结果，以区域实际交通流量与区域最大交通流量之比作为流量指标，以反映潜在交通流量，具体指标如下：

1.2MM-SVR预测模型

由于道路拥堵状况变化过程为状态连续、参数离散的马尔科夫过程，因此本文基于历史数据构建马尔科夫链预测模型。然而，在连续状态的马尔科夫过程中一步转移概率难以获得，因此本文引入支持向量回归机方法对连续状态进行预测，并构建具有马氏链预测状态的MM-SVR模型。

1.2.1道路拥堵马氏描述

此时回归问题转化为线性二分类问题，因此本文将道路周一～周四的拥堵系数作为训练集，按照时间顺序，以n个状态作为一组输入变量，将下一状态的真实值作为预测标签，进行滚动训练。

在训练过程中，考虑到数据在样本空间内线性不可分，因此引入核函数与惩罚因子，并使用网格寻优法寻找最优参数，其基本原理如下：当构造的两类样本D⁺、D^-线性不可分时，通过对硬间隔的软化以及引入罚参数，同样可以考虑在高维空间构造超曲面，以达到回归目的。

在上述模型基础上，根据所给道路的当前交通流状态，对新增车辆进行通行拥堵预测，即测算当通行车辆数量增加时，各路段拥堵程度所受影响。

1.2.3模型检验

均方误差（Mean Squared Error，MSE）是衡量“平均误差”一种较方便的方法，可以评价数据变化程度，越趋向于0说明预测精度越好。平方相关系数（squared CorrelationCoefficient，SCC）是用于反映变量之间相关关系密切程度的统计指标。两种指标计算公式如下：

2实证分析

本文数据包含深圳市局部地区道路的交通卡口监测数据与互联网导航平台数据，具体如下：

（1）该区域内10个卡口所在位置信息（包括检测点名称、方向、所属道路），以及2018年3月25日～31日卡口的过车记录数据。数据包括通过该卡口的車辆车牌号码（车牌号已作脱敏处理）、车牌颜色、时间、车道ID。

（2）浮动车轨迹数据。采集2018年3月25日～31日（7天）途经研究片区内的所有深圳市出租车、公交、“两客一危”车辆、泥头车、重型半挂车、教练车的车辆GPS轨迹数据。该数据包含定位时间、车牌（已作脱敏处理，与卡口数据不关联）、经度、纬度、行驶记录速度、卫星速度。

（3）道路ID属性表。提供了道路ID、道路等级与道路形状坐标。

为验证该预测模型的有效性，对福龙路横龙山路段数据进行整理。以2分钟作为时间间隔，统计整理该路段2018年3月25日～31日内道路交通流的车流量和速度，并根据上文提出的道路指标计算方法对相关数据进行处理，选取工作日（3月27日）与周日（3月25日）进行道路拥堵系数预测如图1、图2所示。

从图中可以看出，3月27日从8：00开始拥堵指数上升，直到2l：00左右才开始下降，且在9：00～10：00，18：00～19：30达到日内峰值，而3月27日的拥堵指数则在白天全天都保持很高的值，这与工作日的早晚高峰以及周末的出游高峰相对应，表明本文构建指标能够很好地反映道路实际拥堵状况。

将获得的道路状态变量作为基于SVR的预测模型训练样本集，并使用训练所得模型预测当天接下来的道路状态及其趋势。训练集分别使用3月26日～3月29日共2716个状态指标，测试集时间段为3月30日。

从表1中可以发现，在以上两个检验指标中，选择四阶MM-SVR模型时，其MSE与R方系数均为最佳，因此选用四阶MM-SVR模型。

图3为3月30日全天的预测数据与真实数据图，通过图像对比发现，文中模型的预测结果与实际数据吻合良好，能够准确预测道路状态趋势。

预测的交通流绝对误差如图4所示，绝对误差量为真实数据与预测数据之差。从图4中可知预测的整体误差较小，93%的误差都在[-0.05，0.05]之间，只出现了某些相对较大的误差，使用Adaboosting、SVR模型对相同数据进行预测，预测精度比较如表2所示。

由表2可以看出，无论是在拟合系数还是预测误差上，本文模型均优于单独使用的其它机器学习模型。

3结语

本文使用马尔科夫链与支持向量机相结合的MM-SVR模型，构建一个针对道路拥堵情况评价的预测模型，即通过构建交通拥堵系数指标，根据已有历史数据，对某段时间的交通拥堵情况进行预测。实验证明该模型可以实时反映出当前道路的交通拥堵情况，并可根据预计新增车辆数量给出较为精准的拥堵情况预测，从而为交通部门实时监控交通状况，并实施及时的交通管制措施提供参考。

本文在实例验证中使用其它机器学习算法进行对比实验，实验结果证明，本文模型在无论在拟合程度还是预测误差上，均优于其它单独使用的机器学习算法。当然，本文也有许多不足，例如本文假设车牌类型相同的车辆车型也相同，而在实际生活中，不同车型也会对道路拥堵情况造成影响，这些有待今后进一步研究。