基于多幂次趋近律的驱鸟机器人路径跟踪控制研究

赵欣洋，刘志远，王化玲，晁战云，初洪波

（1.国网宁夏电力有限公司，银川 750000；2.山东鲁能智能技术有限公司，济南 250000；3.华通科技有限公司，河北 廊坊 065201）

随着国家对生态环境保护力度的加大，鸟类生存范围不断扩大，鸟群不断增多，由鸟类导致的变电站事故层出不穷。近年来，变电站事故很多是由鸟粪引起绝缘子及其周围电场的闪落，筑巢引起的线路接地故障等，电网的安全运行受到了严重威胁［1］。因此，对由鸟类导致的变电站故障进行针对性分析，并制定相应的防治措施，研发出科学有效、环保安全的驱鸟装置，对变电站以及输电线路的安全保障具有重要意义。

常见的驱鸟装置有驱鸟刺、超声波驱鸟器、声音驱鸟器、智能型驱鸟器等［2］。利用机器人来完成驱鸟工作不仅可以节约大量的人力物力资源，还可以增大巡检空间，得到实时反馈信号，在判别鸟的运动轨迹上较大程度地增加了智能性，可实现多方位跟踪驱鸟。然而，在变电站中，各种电力设备交错复杂，若要实现机器人驱鸟工作的精准运行，对其路径进行精准控制是关键。在围绕机器人路径控制问题上，国内外学者都进行了大量研究，现有的路径追踪控制方法主要包括：自适应控制法［3-6］、模糊控制法［7-9］、Backstepping法［10-12］、神经网络控制法［13-14］、线性反馈化法［15-16］、滑模控制法［17-21］等。

自适应控制和滑模控制的结合提高了闭环系统的连续性，降低了外部干扰对整个系统的影响，实现了驱鸟机器人对参考路径的全局跟踪［4］。唐小涛等［9］应用反演控制算法，结合李雅普诺夫自适应率，将系统分解成多个子系统，设计出一种满足移动机器人动态性能指标的控制器。赖欣等［12］针对受速度跳跃影响的移动机器人，基于神经网络系统的方法，提出一种能产生零初始速度连续平稳机器人控制信号的算法，此种方法还可处理跟踪误差非常大的情况。郑一力等［15］采用的PID控制法在一定程度上控制了机器人的方向和速度，但是在精度上达不到要求。张鑫等［19］将滑模控制和RBF神经网络结合，一定程度提高了不确定性扰动下的路径跟踪性能。

在上述控制方法中，由于移动机器人的运动方向、速度和路径都是非线性的，单独使用线性控制会造成较大误差，因此线性控制方法一般都是结合其他非线性控制方法使用。模糊控制中控制方程的数学模型，虽然语言简单，但缺乏系统性，难以定义控制目标；自适应控制方法在实际运用中难度较大，估计参数与控制精度存在较大误差，且成本较高；反推控制方法由于是将系统分为不超过阶数的子系统，然后给每个子系统设计对应的李雅普诺夫函数，这种方法设计过程较为复杂，难度较大；滑模变结构控制法具有算法简单、鲁棒性强、响应速度快和可靠性高等优点，被广泛应用于精度高的确定性运动控制系统中。

本文设计的驱鸟机器人为四轮驱动的路径追踪式机器人，是一种典型的非完整控制系统，针对其运动受环境因素影响较大，具有变量多、非线性和耦合性强的特点。从控制角度出发，首先建立高精度的数学模型，然后对传统滑模控制方法进行改进，提出一种多幂次趋近速率的滑模控制方法，以解决驱鸟机器人实时路径跟踪问题。该控制方法使得状态在趋近滑模面的过程中，拥有较快的速率，且能削弱滑模变结构控制固有的抖振，具有较高的研究价值。

1 四轮驱动驱鸟机器人运动学分析

1.1 驱鸟机器人运动模型

本文所设计的驱鸟机器人模型如图1所示，是一个典型的非完整轮式移动机器人模型，其几何模型如图2所示。驱鸟机器人的4个驱动轮安装在不同的轴承上，其移动和转动方向是由直流电机提供转动所需的扭矩来实现的。采用四轮驱动，相较于两轮，其优点在于提高了移动机器人的通过性、爬坡性、转弯性能、启动和加速性能以及直线行驶稳定性。

图1 驱鸟机器人模型

图2 驱鸟机器人几何模型

假定机器人的运动坐标位于质心，忽略轮子的摩擦力，由图2可知其运动方程为

其中J（θ）∈R3×2，v∈R2分别代表满秩的速度变换矩阵和速度向量；v（t）∈R表示机器人质心的线速度；ω（t）∈R表示机器人质心的角速度。

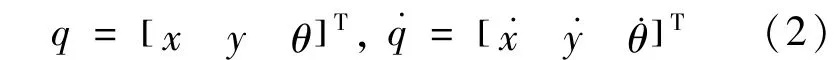
由于不考虑轮子的摩擦力，假设为纯滚动状态，则可以得到

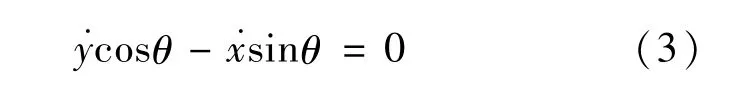
为了确定跟踪控制问题，本文给移动机器人设置了轨迹参考值为

其中：qr（t）＝［xr（t）yr（t）θr（t）］T∈R3表示期望的时变位置和方向轨迹；vr（t）＝［xr（t）ωr（t）］T∈R2表示参考的时变线速度和角速度。

在式（3）中，构造vr（t）是为了产生所需的笛卡儿路径qr（t）。在实际应用中，vr（t）＝［xr（t）ωr（t）］T和它的导数是有界且已知的。

当q→qr或t→∞时，需要找到合适的速度控制速率vc（t）＝［xcωc］T。一般来说，轨迹追踪问题是跟踪一个参考移动机器人已知的姿势［xr（t）yr（t）θr（t）］T。因此，本文定义误差为参考值和实际值之差，其表示为 ~q＝qr-q＝［（xr-x） （yr-y） （θr-θ）］T。

图3 姿态误差坐标

qe为姿态跟踪误差，即参考姿态qr相对于固定在实际驱鸟机器人的框架的转换。误差率表示为

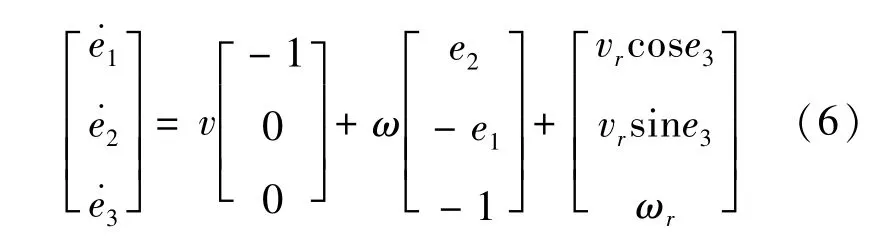
在确定姿态追踪误差后，需要为驱鸟机器人提供姿态误差控制率。式（7）是一种常用的速度控制命令，使用倒步法，主要用于移动移动机器人的追踪问题。

其中k1、k2、k3都是正常数，vr＞0。

1.2 直流电机的数学模型

本文驱鸟机器人的4个车轮都是靠直流电机来驱动，且通过改变左右两侧驱动轮的线速度和角速度来控制运动轨迹。其工作原理是：将直流电从两电刷之间通入电枢绕组，通电后的电枢绕组在磁场中旋转，产生感应电动势，进而产生电磁力，从而驱动车轮前进。

忽略电机的电磁干扰、电枢反应、磁饱和、磁滞损耗等因素，建立电机的数学模型。

电压平衡方程为

其中：R为电阻；L为定子电感；ε为反电动势；i为相电流；u为定子相电压。

电磁转矩方程为

其中：Te为电磁转矩；J为转动惯量；ω为角速度；KT为转矩系数。

直流电机绕组的动态方程为

其中Kε为反电动势系数。

联立式（8）～（10）得动力学方程为

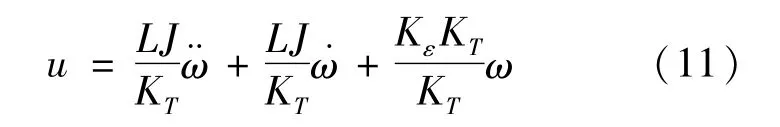
对式（11）进行拉普拉斯变换得直流电机传递函数为

2 滑模控制器的设计

滑模控制结构框图如图4所示。假设直流电机的期望角速度为ωd，实际角速度为ω，则状态变量忽略系统的不确定量和其他扰动变量，则系统的状态方程为

其中d（t）为扰动量总和。由于采用多幂次趋近律来控制，要设计3阶滑模控制器，即设x3为x1的积分，那么式（13）可以写为：

再将其写成矩阵形式，则

其中

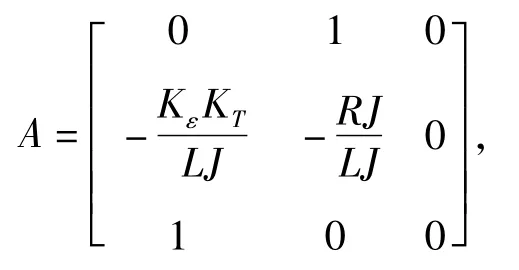
记f（x）＝Ax＋E，g（x）＝Bu。

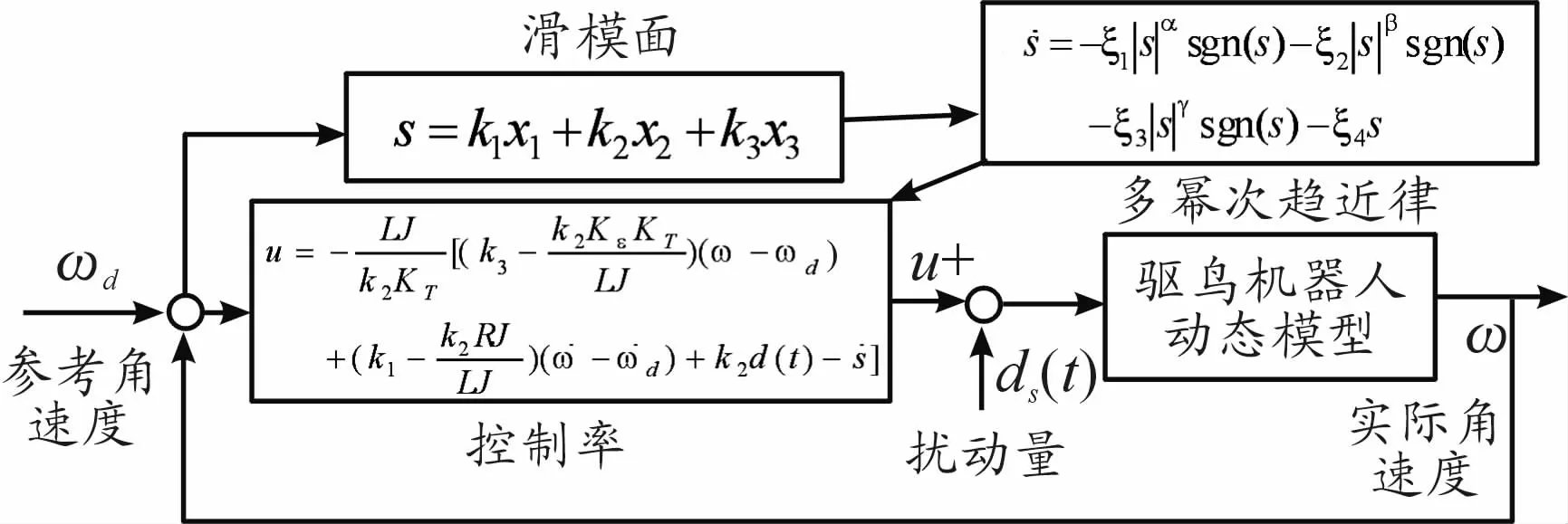
图4 驱鸟机器人滑模控制结构框图

2.1 滑模面的设计

设滑模切换函数为

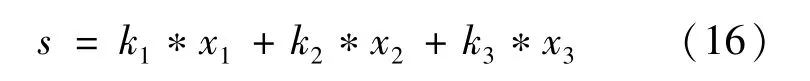
其中：k1，k2，k3＞0，k1，k2，k3参数的设计必须保证系统在有限时间内任意初始状态都能达到滑模态，且满足赫尔威茨（Hurwitz）条件。

对（16）求导得

联立式（14）得：

2.2 趋近率的设计

考虑基于传统滑模控制器无法有效去除抖振，且收敛速度慢等因素，本文采用的多幂次趋近律为

其中：ξ1＞0；ξ2＞0；ξ3＞0；ξ4＞0；α＞1；0＜β＜1。

γ的取值为

设李雅普诺夫函数为

对其求导有

联立式（19）得：

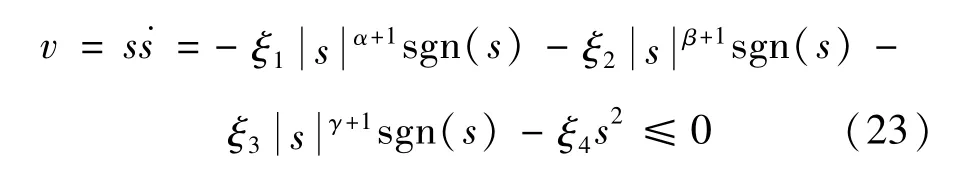
由李雅普诺夫稳定性判定定理可得，系统渐进稳定，即在有限时间内，系统可由初始状态到达滑模面。且当s＝0时，˙s＝0，即保证系统不会发生抖振现象。

联立式（18）和式（19）得

即多幂次滑模控制器的控制率为

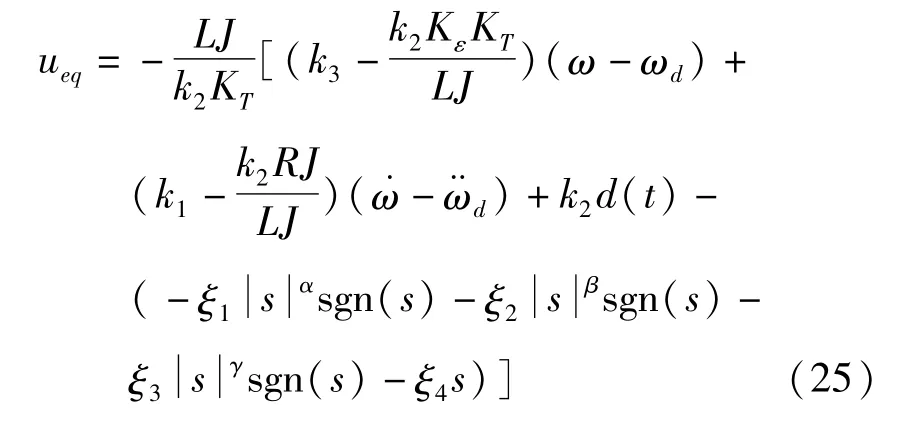
3 稳定性分析

滑模控制的稳定性考察的是所设计的系统能否在状态变量平面上运行至滑模切换面，最后沿着此轨道抵达相平面原点，达到系统稳态。本文将传统滑模控制系统与所设计多幂次趋近律滑模控制系统进行稳定性对比分析。

图5为两种不同控制策略下的驱鸟机器人直流电机系统状态变量相图。图中AB段为趋近阶段，BC段为滑动阶段。图5（a）显示：传统滑模控制的系统状态变量相图存在滑模切换抖振区域，系统无法快速沿切换轨迹回到0点（相平面原点），系统有较大的稳态误差。由图5（b）可知：本文研究的多幂次趋近律滑模控制变换器的瞬态响应的系统状态能够沿切换轨迹快速回到状态变量中心原点，其抖振影响较小，证明该方法的轨迹跟踪更精确。

4 仿真分析

为了验证本文所提出的多幂次滑模控制方法对驱鸟机器人轨迹精确跟踪的有效性，在Matlab环境中对其进行建模仿真。所用直流电机参数为：P0＝0.2 kW，n0＝3 000 r／min，U0＝12 V，R＝0.64Ω，I0＝1.5 A，L＝10 mH，Kε＝0.037 rad／s，J＝0.06 g·m2，KT＝0.035 N·m／A。滑模面系数分别为：k1＝1，k2＝3.5，k3＝0.05；趋近律系数分别为：ξ1＝1.2，ξ2＝0.7，ξ3＝1.4，ξ4＝0.8，α＝1.6，β＝0.8；白噪声干扰为：d（t）＝50*rand（1，1）。

图5 驱鸟机器人直流电机系统状态变量相图

仿真结果如图6、7所示。采用多幂次趋近律滑模控制方法，驱鸟机器人可以较好地沿着理想轨迹运动，其位置和速度跟踪的速度都较小，且收敛速度较快，鲁棒性好，有效解决了传统滑模控制器不能去除抖振的问题，满足驱鸟机器人所需的快速精确定位要求。

图8为所设计的多幂次趋近律滑模控制器在不同k值下的驱鸟机器人直流电机系统趋近律相轨迹图。由趋近过程图可以看出，随着取值k的不断增大，其趋近时间越短，系统完成滑模面切换后进入稳态最后趋近原点，不存在大幅度抖振，控制效果显著。

图6 位置跟踪曲线

图7 速度跟踪曲线

图8 不同k值下的系统趋近律相轨迹图

5 结束语

本文提出一种多幂次趋近律滑模路径跟踪控制方法。忽略驱动轮所受的滑动摩擦力，基于实际角速度和期望角速度误差搭建并分析了驱鸟机器人运动模型，根据直流电机数学模型设计了新型滑模控制器，并利用李雅普诺夫定理证明了该滑模控制系统渐进收敛。仿真实验结果表明：相对于传统的滑模控制策略，该方法鲁棒性更强，其位置精度和速度跟踪精度都较小，且可以削弱抖振现象，使得机器人的运动跟随理想轨迹，研究成果为变电站实现精准驱鸟提供了有效依据。