基于离散元法的双卧轴搅拌机工作性能的分析与研究

张 宏

（山西省晋中路桥建设集团有限公司，山西 晋中 614000）

水泥混凝土、沥青混凝土等搅拌设备的性能与研究进展，在很大程度上影响了道路、桥梁、房屋等建筑与基础设施的安全性与使用寿命，因此对相关搅拌设备开展研究，通过改变其运动参数与几何参数，从而提高搅拌的均匀性变得尤为重要［1］。但目前已有的研究方法存在较大的局限性，不能完全满足并符合实际搅拌的工作要求［2］。

离散元法是用来解决不连续介质问题的数值模拟方法，其基本思想是把散体群粒简化成一个具有质量和形状的颗粒的集合，被广泛应用于道路建设、农业工程等行业［3-5］。蔡改贫等［6］通过离散元法研究了岩石在受到冲击进行破碎的情况下的受力与裂纹出现、延伸的关系，解释了颗粒体破碎的微观过程。李建生［7］应用离散元软件EDEM得到了立轴式破碎机喂料环角度、转子与喂料盘高度对破碎处理量的关系。王家全等［8］采用EDEM软件分析了土工格栅在新旧路堤的受力分布，以及加筋区域土体细观参数的变化。离散率为搅拌均匀性能的最主要评价指标，客观反映了单位体积内颗粒的均匀程度，其值越小则搅拌性能越好，反之则越差。本文以“JS3000”型号双卧轴搅拌机为研究载体，对其搅拌过程进行研究分析，在此基础上，以离散率为搅拌均匀性能的评价指标，运用离散元软件EDEM作二次正交旋转组合试验，旨在利用一定的计算方法获得搅拌机的最优参数组合，为搅拌机的优化提供理论依据，促进建筑行业与筑路行业的发展。

1 模型的建立

1.1 离散元算法计算流程

在离散元法的研究中，若颗粒间表面没有黏附作用，设置颗粒与几何体、颗粒与颗粒之间的接触模型为Hertz-Mindlin（no slip）built-in［9］。其计算程序流程如图1。

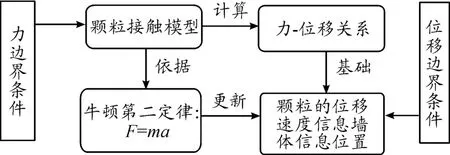
图1 离散元法计算流程

1.2 搅拌过程模型

将搅拌过程中不同颗粒含量的变化视为随机的马尔柯夫过程，使得搅拌过程可以采用柯尔莫高洛夫微分-差分方程表达［10］，即

式中：Nf为时间为t1，搅拌机内某成分结合数量的随机值；PNb（t）为随机取值Nf取整数值Nb的概率，即PNb＝p｛Nf（t）＝Nb｝；γNb为常数。

对于圆柱壳体搅拌机（图2）的搅拌过程，可以采用柯尔莫高洛夫方程模拟搅拌动态变化过程的扩散过程，即

式中：M为搅拌物中关键成分的含量（kg）；t为搅拌时间（s）；v为搅拌物的轴向速度（m／s）；c1、c2分别为搅拌物的轴向、径向扩散系数；l、r分别为搅拌机内腔的轴向与径向坐标，轴向、径向扩散系数的大小主要取决于颗粒尺寸、充盈率以及搅拌速度等。但除上述搅拌过程的分析之外，混凝土等属黏-塑混合物，且搅拌轴上的叶片运动破坏了颗粒行为的连续性，因此混凝土的离散率与其内部运动受多因素影响。本研究通过改变充盈率、搅拌轴转速、叶片安装角等参数，间接影响离散率。

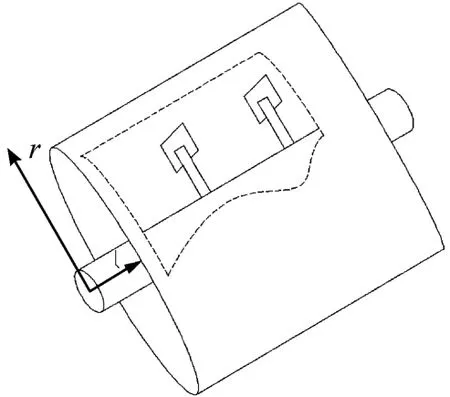
图2 搅拌机模型简图

2 基于EDEM 的辅助参数设计和优化

通过前述对搅拌工作过程的分析，为优化搅拌机的结构参数和运动参数，提高其性能，选取搅拌轴转速、充盈率、叶片安装角3个因素进行仿真试验。试验采用二次回归正交旋转组合设计。

2.1 颗粒模型及几何模型的建立

搅拌机中水泥、砂子、碎石的几何尺寸等为随机变量，同样是影响搅拌性能的主要因素。本研究以矿渣硅酸盐水泥、粗砂、石子为研究对象，采用落料试验（图3）测得不同颗粒塌落后的休止角，通过离散元公司所提供相关网站输入不同颗粒休止角获得其部分物理特性与力学特性［11］。对华中科技大学所购买某厂家所产的双卧轴搅拌机（图4）进行测量，并建立其三维模型，由于在离散元仿真模拟中只需将与颗粒接触的几何部件导入，所以将双卧轴搅拌机模型进行简化，应用三维软件UG对其建模，如图5所示。

图3 落料试验装置

图4 双卧轴搅拌机

图5 双卧轴搅拌机仿真模型

2.2 EDEM 软件仿真

根据文献、测试结果及材料库，水泥、砂子、碎石颗粒以及双卧轴搅拌机的物理特性和相互间的力学特性如表1（其中密度为测试结果，泊松比与剪切模量由已有文献得出）、表2所示［12-14］。

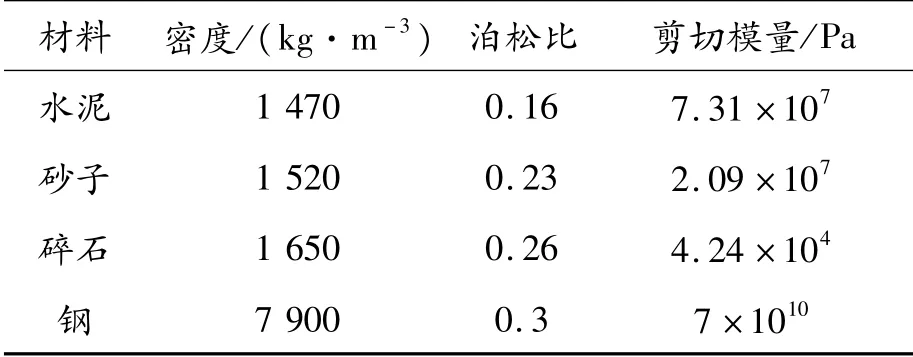
表1 仿真物理特性

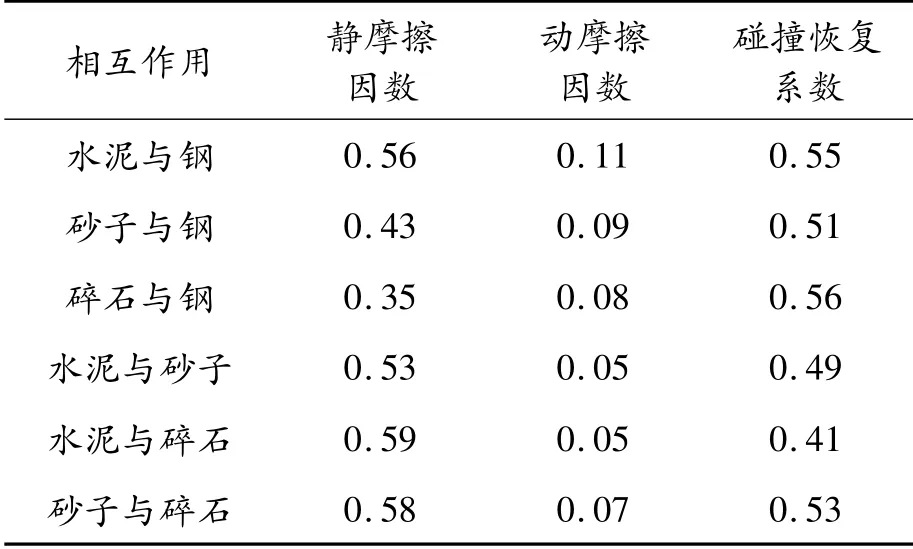
表2 仿真学特性

由于砂子、碎石颗粒表面无黏附作用，加之前文对离散元模型的研究得知选择Hertz-MindLin（no slip）built-in为仿真接触模型。但水泥具有黏结的特性，且EDEM中的JKR模型适用于具有黏结作用的仿真，因此通过API接口对该接触模型进行二次开发［15］。命令水泥的接触模型为编译后的JKR模型，其余接触模型为Hertz-MindLin（no slip）built-in。本研究以混凝土强度等级为C25的配比为依据，同时为了保证仿真时双卧轴搅拌机工作有足够的颗粒和仿真时间，设置生成水泥颗粒数、砂子颗粒、碎石颗粒目分别为90 000、32 000、17 000［16］，半径平均值为1、7、23 mm，采用正态分布的方式生成颗粒尺寸，标准差分别为0.086、0.102、0.093，同时对不同颗粒进行不同颜色的着色，设置固定时间步长为Rayleigth时间步长20%，仿真时间共31 s，前7 s为颗粒工厂生成各类颗粒的时间。同时为计算反映搅拌均匀性的离散率，对该双卧轴搅拌机进行网格划分，如图6所示。

图6 网格划分

2.3 仿真试验因素与指标

本研究卧轴搅拌机的工作性能评价指标为离散率（L），该值越大，搅拌效果越不均匀，反之则搅拌效果越均匀［17］。均匀度的离散率的求解过程为：令卧轴搅拌机内3种颗粒数目分别Nd、Ne、Nf，搅拌机内颗粒总数目为N＝Nd＋Ne＋Nf。同理，每个网格中颗粒总数目与3种颗粒数目分别为n、nd、ne、nf，实际与理想状态下颗粒的均匀程度偏离程度总偏离程度为

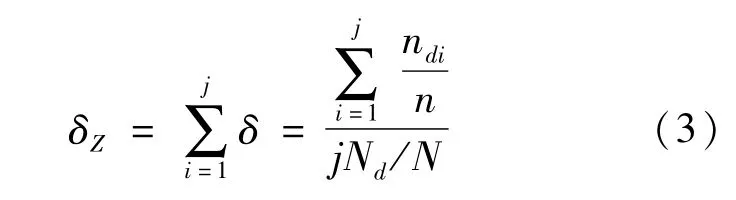
式中j为仿真中网格的总数目，则均匀度离散率L为

根据前述理论分析及卧轴搅拌机作业要求，合理地控制试验因素变化范围，每号试验重复9次，取其平均值作为试验结果，因素水平编码如表3所示，试验方案与结果如表4所示。

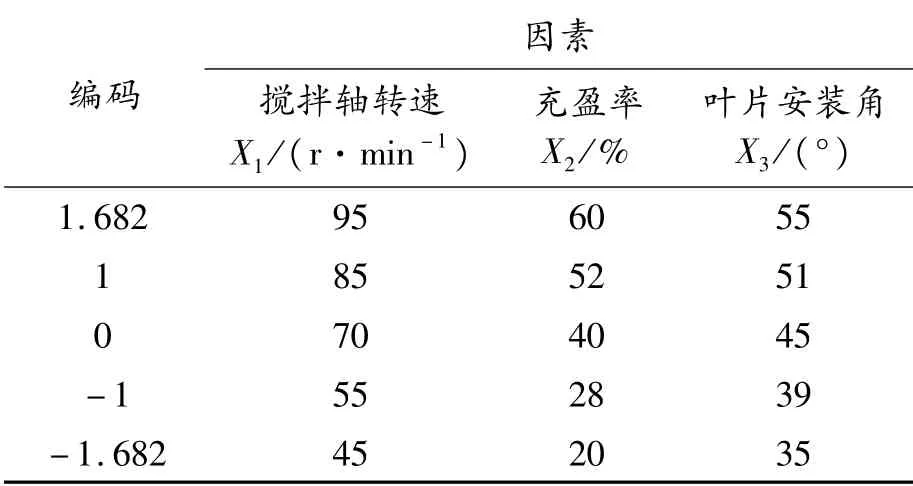
表3 因素水平编码

表4 试验方案与结果

2.4 试验结果及分析

2.4.1 离散率

运用spss数据分析软件对表4离散率试验结果进行回归分析，其回归方程检验数据如表5所示。

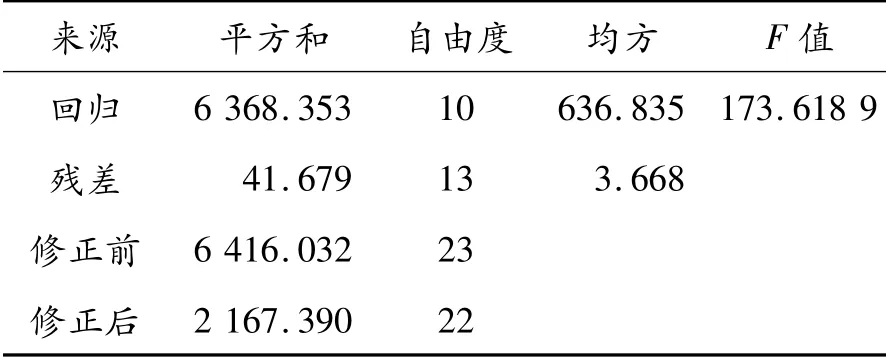
表5 离散率回归方程检验表

查F表得F0.01（10，13）＝4.10，F＝173.619＞F0.01（10，13），因此回归方程高度显著，其二次回归方程模型为

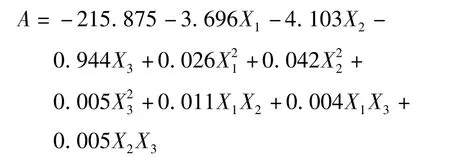
运用Matlab绘制三维等值线图，如图7所示。分析图7可以得知，将充盈率固定在零水平时，随着搅拌轴转速的增大，离散率呈现先下降后上升的趋势，这主要是由于当转速较低时，颗粒运动的循环次数较低，搅拌不均匀，因此其离散率较大。但当转速增大到一定数值时，搅拌机内颗粒具有较大离心力，从而同样破坏其均匀性，造成离散率增大。将搅拌轴转速固定在零水平时，出现了随着充盈率的增加，离散率先下降后上升的现象，这主要是因为当搅拌机内充盈率较低时，相互作用的颗粒很少，减小了颗粒之间的摩擦力，不能形成大范围内的运动，从而造成了离散率的增大。但随着充盈率增大，当其超过一定数值时，搅拌机内部留给颗粒运动的空间过小，减小了颗粒整体的沸腾作用，同样出现了搅拌不均匀，造成了离散率的增加。另外，将叶片安装角固定在零水平时，随着搅拌轴转速的增加，离散率出现了先下降后上升，而将搅拌轴转速固定在零水平时，叶片安装角的增加对离散率的影响不大。将叶片安装角固定在零水平时，随着充盈率的增加，离散率出现了先下降后上升，而将充盈率速固定在零水平时，叶片安装角增加对离散率的影响不大。除此之外，由回归方程和三维等值线图可知，在试验范围内三因素对双卧轴搅拌机离散率显著性影响大小顺序是充盈率、搅拌轴转速、叶片安装角。

图7 离散率等值线图

2.4.2 双卧轴搅拌机性能优化

根据优化数学模型和搅拌机各性能评价指标的回归方程，利用Matlab中非线性优化fmincon函数，以F（max）＝L即离散率最小为条件进行寻优处理。优化处理结果为：取搅拌轴转速为61.93 r／min，充盈率为38.02%，叶片安装角为46.34°。在此条件下进行仿真验证试验，试验表明双卧轴搅拌机离散率为6.22%。

3 试验验证

为验证离散元软件EDEM 研究结果的可行性，在华中科技大学土木工程与力学学院工程结构分析与安全评定湖北省重点实验室开展试验验证。在充盈率为40%，叶片安装角为35°、39°、45°、51°、55°的情况下，使用变频器令搅拌轴转速分别45、55、70、85、95 r／min，用混凝土多功能无损检测仪SCE-MATS（图8）对不同转速下的离散率进行测定。试验与仿真结果如图9所示。

图8 SCE-MATS型混凝土多功能无损检测仪

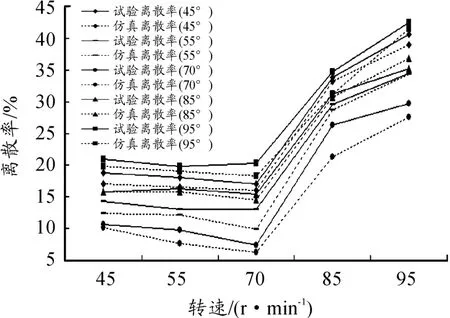
图9 不同转速下试验与仿真的颗粒离散率对比

从图9可以看出，在不同叶片安装角角度下，随着转速的增加，试验与仿真的离散率变化趋势基本一致，试验所得离散率略大于仿真所得离散率。造成该现象的主要原因有：试验中叶片倾角的加工存在误差，无法完全达到设定值。除此之外，由于传动过程中摩擦等原因，造成了试验搅拌轴转速与设定值的偏差。当转速低于70 r／minj时，离散率波动较小，试验所得离散率与仿真所得离散率差异较小；当转速高于70 r／min时，离散率波动较大，试验所得离散率与仿真所得离散率差异较大，其中最大差值为5.07%。仿真分析结果与试验结果吻合，证明了采用离散元法研究双卧轴搅拌机工作性能、搅拌均匀性的可行性。

4 结论

1）运用EDEM作正交搅拌虚拟试验，通过二次回归正交旋转组合试验建立了以离散率为考察指标的回归方程。运用Matlab绘制离散率的等值线图，得到在试验范围内三因素对离散率显著性影响大小的顺序是充盈率、搅拌轴转速、叶片安装角。

2）确定了该型双卧轴搅拌机的最佳参数组合，当搅拌轴转速为61.93 r／min，充盈率为38.02%，叶片安装角为46.34°时，搅拌最均匀，此时双卧轴搅拌机离散率为6.22%。

3）通过不同叶片安装角、不同转速下离散率的仿真与试验结果对比，得知两者结果变化趋势一致，结果基本相同。