带偏好的交叉航路角度优化模型

戴福青 ，庞笔照 ，赵元棣

（中国民航大学空中交通管理学院，天津 300300）

交叉航路空域是飞行拥堵、航班延误、安全事故易发区域，也是空中交通航路网中的运行瓶颈之一，其结构优劣直接影响空中交通流运行安全和效率.研究航路基本相交结构的要素特性，揭示交通流运行参量与航路结构要素间的相互演变关系，可为空域精细化管理理论、空中交通运行瓶颈拥挤识别与预测等[1]提供一定的科学依据，具有重要的研究价值和现实意义.

国内外相关学者针对交叉航路结构优化问题已进行大量研究. 研究视角由以航路网结构优化为目标[2-3]到以优化交叉点位置为核心[4-5]；由航路汇聚点、交叉点数量和布局优化[6-8]到以航路路段长度和交叉角度等要素研究交叉航路结构[9-10]. 优化指标涵盖了安全性[11]、容量[12]、空域复杂性[13]等；相关的模型和求解算法同样丰富，先后建立了基于多目标规划、元胞自动机等数学思想的优化模型，并采用粒子群优化算法、启发式遗传算法等对模型进行了求解.

上述研究成果虽较为丰富，但仍存在以下3大不足：（1） 优化目标大多聚集在安全性、容量等方面，对于节能减排、航班延误等研究尚有不足；（2） 大多未考虑交通量分布对交叉航路结构优化的影响，缺乏对航路资源需求的分析；（3） 大多将优化指标的权重视为相同，忽略了不同空域用户的偏好需求.

针对上述研究不足，本文以交叉航路空域为研究对象，系统研究交叉航路角度优化问题. 通过深入剖析航路基本相交结构要素特性与飞行时间和油耗的关系，在交叉航路交通量分布统计的基础上，综合考虑空管、航空公司等空域管理及使用方的需求，建立带偏好的航路交叉角度优化模型及算法，实现对交叉航路空域资源的优化配置，从而提高空域资源使用效率及空域精细化管理能力，缓解交叉航路日益严重的空域拥挤和飞行延误问题.

1 航路节点构型

基于雷达管制，现行空域可简化为二维结构，航路之间的关系可表示为平行或相交. 相交航路节点处的空域容量、运行安全等指标主要受相交航路数量、长度和角度等因素影响[9]. 相交航路数量越多，相交节点处空域结构越复杂；航路长度具有边际特性，超过阈值后，相交节点处空域各项评价指标不受长度影响；航路相交角度的大小根据航路方向和结构确定，角度太小时，因侧向安全间隔要求，部分航班需减速或盘旋等待以满足过点间隔限制，角度太大时，相交航路占用空域过多，造成空域资源浪费.此外，空中交通对交叉航路资源的需求呈现非线性分布特征[14]，根据交通量分布对交叉航路角度进行优化，可以有效实现空域精细化管理，提高空域资源使用效率.

1.1 航路基本节点构型

根据各航路交通流运行方向和相交位置，航路基本相交构型可分为汇聚结构、分散结构和转弯结构[2]，如图1所示，3种结构下交通流存在畅行态和滞留态两种状态.

汇聚结构如图1（a），航路相交角度较大时呈现畅行态，航班之间满足侧向安全间隔，运行顺畅；角度过小时表现为滞留态，为满足侧向安全间隔，管制员往往要求后机减速等待或在航路盘旋等待，直至与前机建立安全间隔，这就增加了飞行时间和燃油消耗. 分散结构如图1（b），畅行态和滞留态发生原因与汇聚结构类型一致. 转弯结构如图1（c），转弯角度较小时表现为畅行态；转弯角度过大时表现为滞留态，因航路中运行的航班速度大，转过较大角度时，受转弯率限制，其飞行距离也将大幅增加，飞行时间和油耗随之增加. 其中： α 、β、θ 分别为畅行态对应的汇聚交角、分散交角和转弯交角；α′、β′、θ′分别为滞留态的汇聚交角、分散交角和转弯交角；Dsep为航路侧向安全间隔.

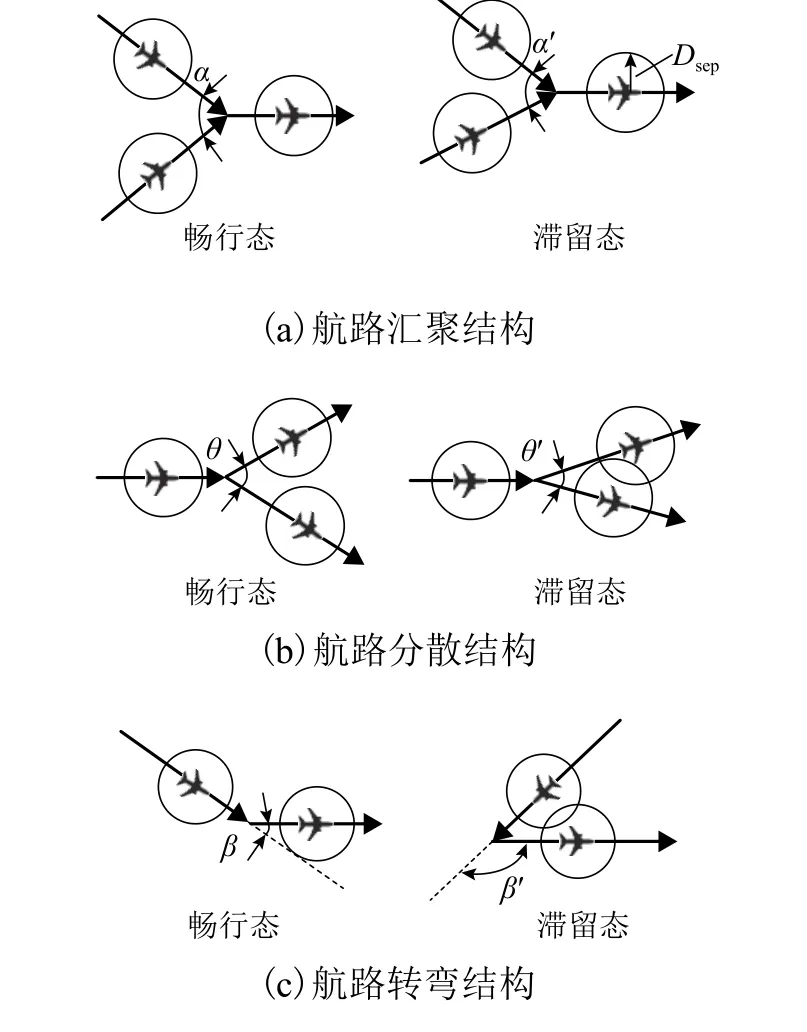
图1 航路基本相交构型示意Fig.1 Diagram of fundamental crossing air routes

交通流发生滞留时，空域内航班飞行时间和油耗增加，因此很有必要对航路相交角度与航班飞行时间和油耗的关系进行研究.

1.2 飞行时间和油耗与航路交角的关系

相交航路空域结构复杂，航班为满足安全间隔要求机动较多，其速度、高度、航向等飞行参数的变化呈非线性特点，直接建立数学模型难以准确描述航路交角与航班飞行时间和油耗的关系. 因此，本文采用计算机仿真方法，利用全空域建模仿真平台（terminal airspace and aerodrome modeling，TAAM）建立相应的航路构型，分析航班飞行时间和油耗随航路相交角度变化的关系.

仿真实验采用控制变量法，使用相同的航班计划数据和空域运行规则，设计不同的航路相交角度对应的空域结构进行实验. 为确保实验结果具有普适性，仿真实验采用了典型的航班计划数据，其中包含100架航班样本，重型机、中型机、轻型机的比例按 2016年国内飞机保有量数据取为0.13∶0.81∶0.06[15]；仿真交通流的最小侧向安全间隔为10 km；航班飞行高度层由仿真软件依据航班的机型和航程从最佳飞行高度依次分配，且无空中立交桥限制. 根据航路结构的组成规则，咨询空域规划方面专家，取α ∈ [0°,120°]、 θ ∈ [0°,120°] 、 β ∈ [0°,140°] ； 根 据 已有研究[9]，本文取航段长度阈值为70 km.

结合图1分别对3种航路相交结构每10° 调整一次构型进行仿真实验，统计对应的100架航班从进入到离开实验空域总用时和总油耗，求和取平均值得到单位航班在3种不同航路结构下飞行时间和油耗随航路交角变化的关系如下.

图2为单位航班飞行时间随航路交角的变化关系. 汇聚、分散和转弯结构下，飞行时间随角度增大均呈先减小后增大趋势，转弯结构下航班机动范围大，飞行距离长，相同角度对应的飞行时间较汇聚和分散结构更长.

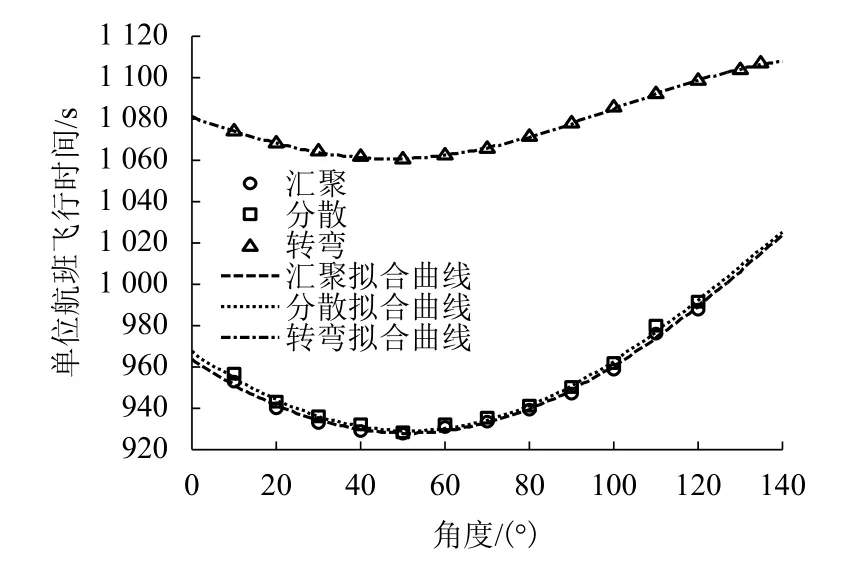
图2 单位航班飞行时间随角度变化关系及拟合结果Fig.2 Relationships and fitting results of unit flight time change with angles

图3 为单位航班油耗随航路交角的变化关系.汇聚和分散结构下，油耗随角度增大呈先减小后增大趋势；转弯结构下航班转过角度越小，单位航班油耗也越小. 此外，汇聚角度变化对单位航班油耗影响最大，且存在明显的最优角度区间；分散结构下单位航班油耗对角度变化不敏感，最优角度区间较大.

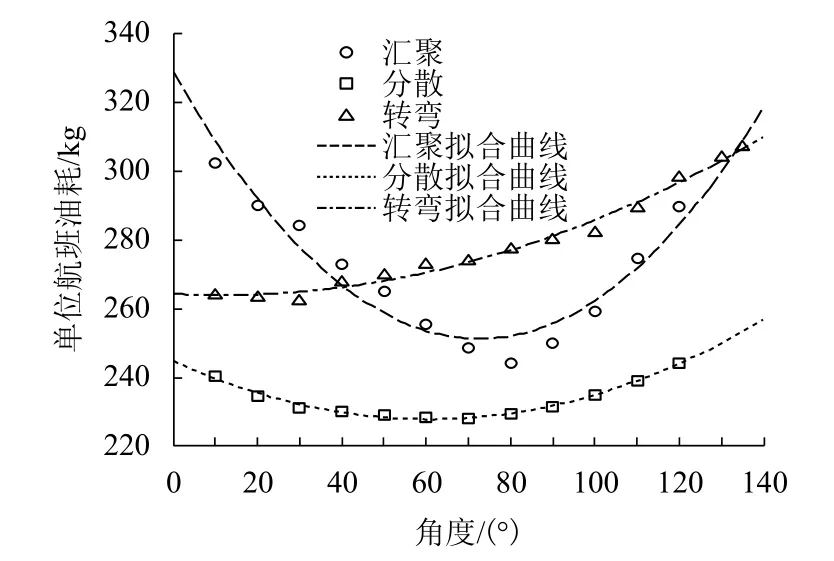
图3 单位航班飞行油耗随角度变化关系及拟合结果Fig.3 Relationships and fitting results of unit flight fuel consumption change with angles

通过上述分析，汇聚、分散和转弯结构下，单位航班飞行时间和油耗都与航路相交角度存在显著的非线性关系. 本文采用5种常用的拟合方法[16]，选取令人满意结果，得到单位航班飞行时间随角度变化的拟合结果如图2，单位航班油耗随角度变化的拟合结果如图3，拟合得到的非线性函数关系如下：

（1） 汇聚、分散和转弯结构下，单位航班飞行时间 t 与 α 、 θ 和 β 的函数关系为

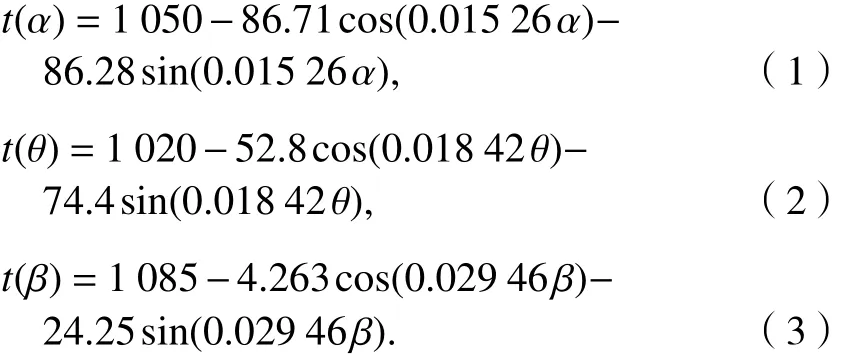
式（1）为汇聚结构下单位航班飞行时间与角度的拟合函数，拟合优度为 0.994 4；式（2）、（3）分别为分散结构和转弯结构拟合函数，拟合优度分别为0.995 0和0.9995.

（2） 汇聚、分散和转弯结构下，单位航班油耗g与 α 、 θ 和 β 的函数关系为

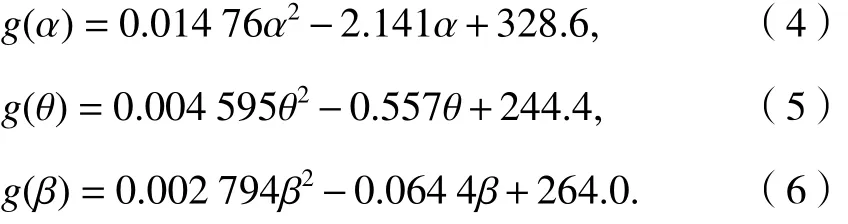
式（4）为汇聚结构下单位航班油耗与角度的拟合函数，拟合优度为 0.920 8；式（5）、（6）分别为分散结构和转弯结构拟合函数，拟合优度分别为0.987 6和0.987 2.

仿真实验采用典型的航班计划数据和相同的空域运行规则，得到航班飞行时间和油耗随航路相交角度变化关系，通过拟合进一步得出对应的函数关系式. 因此，对于其他航路节点构型此函数关系具有一定的普适性，下文将对其进行验证.

2 交叉航路角度优化模型

2.1 问题描述

交叉航路是一种更为复杂的航路相交结构（见图4），其包含汇聚、分散和转弯3种基本结构的共同特性，单位航班飞行时间和油耗随角度变化关系在交叉航路构型中同样适用. 考虑单位航班飞行时间或油耗时，汇聚、分散和转弯3种结构分别存在最优角度取值区间；交叉结构下，基于交通量分布提出3种角度综合取值最优模型，通过使交通分布量越大结构对应的角度取值越优，达到交叉航路角度结构最优化.

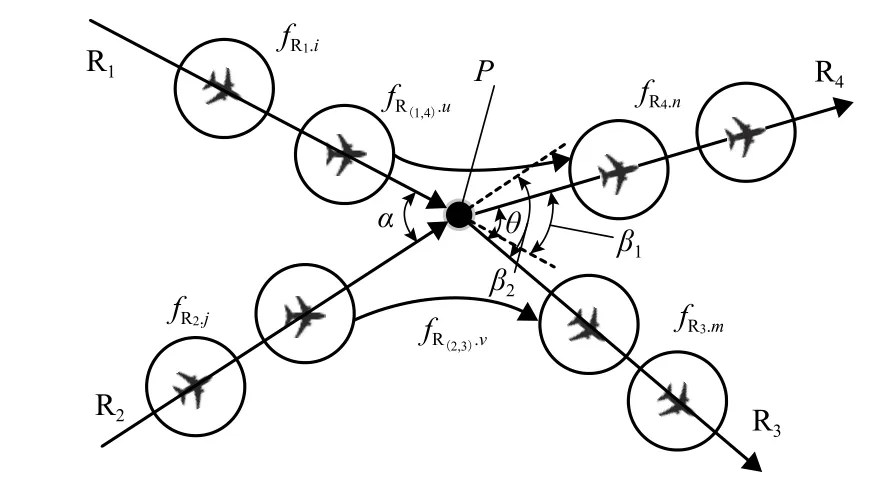
图4 交叉航路构型Fig.4 Diagram of crossing air routes

图4 中: fR1.i、 fR2.j、 fR3.m、 fR4.n、 fR(1,4).u、fR(2,3).v反映交通流大小，下标 i、j、m、n、u、v为不同的航班，R1、 R2、 R3和 R4为航路； fR1.i(fR2.j) 表示航班 i（j）由航路R1（R2）经交叉点P，进入交叉航路空域的交通流； fR3.m(fR4.n) 表示航班 m（n）从航路 R3（R4）离开的交通流；R(1,4)（R(2,3)）表示从 R1到 R4（R2到 R3）的飞越，R(1,2)、R(3,4)分别表示两条航路在P点的汇聚（R1、R2）和分散（R3、R4）； fR(1,4).u(fR(2,3).v) 表示航班u（v）不经过导航台，从航路 R1（R2）旁切飞行加入R4（R3）的交通流；R1和 R2相交于 P 点,构成汇聚结构，汇聚角为 α ；R3和R4构成分散结构，分散角为 θ ；R1和R4、R2和R3构成转弯结构，其对应转弯角度分别为 β1、β2.

2.2 目标函数

交叉航路结构复杂、资源有限，交通高峰时段需求增大，极易在交叉航路空域发生拥堵，致使航班飞行时间增长、油耗增多. 因此，本文从航班飞行时间和油耗这两个角度建立优化目标.

（1） 最小化航班飞行时间

航班飞行时间影响航班延误和空域资源占用，而提高航班准点率、提升空域资源使用效率是民航发展的重要目标. 因此，模型使所有经过交叉航路空域范围的航班飞行总时间T最小，即

式中： FR(1,2)为 汇聚结构对应交通量； FR(3,4)为分散结构对应的交通量； FR(1,4)、 FR(2,3)为转弯结构交通分布量；I、J、M、N、U、V 分别表示 R1、R2、R3、R4、R（1，4）、R（2，3）上的航班集合.

（2） 最小化航班燃油消耗

燃油消耗直接影响航班运行成本和污染物排放，“节油减碳”是我国发展绿色民航的重要目标之一，因此，模型使所有经过交叉航路空域范围的航班总燃油消耗O最小，即

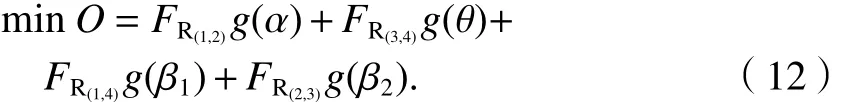
2.3 带偏好的目标函数改进

航班飞行时间和油耗两个目标函数采用多目标求解方法进行计算时权重相等，然而实际运行过程中，由于空管、航空公司等部门往往从自身利益出发，对航班飞行时间或油耗带有一定偏好，为均衡各方利益，满足不同需求，在2.2节基础上提出带偏好的角度优化模型.

由成本指数定义，航班飞行时间和油耗成负相关关系，定量描述为

式中： Ct为时间成本（元/min），由飞行机组小时费、飞机折旧等与时间有关的费用组成； Cf为油耗成本（元/kg），主要受原油市场价格影响； CI为成本指数（kg/min），反映时间成本相对于燃油成本的重要程度，根据已有研究[17]，本文取 CI=11.9 ， Cf=6 .

通过引入时间权重和油耗权重实现对偏好的量化表示，将飞行时间和油耗两个优化目标转变为以航班时间和油耗总成本为目标的带偏好的角度优化模型，表示为

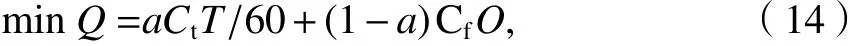
式中：Q为所有经过交叉航路的航班时间和油耗总成本（元）； a 为时间权重， a ∈[0,1.0] ， 1 -a 为油耗权重. a 的取值将影响目标函数解的形式，分别对以下3种情况加以讨论：

（1） 当 a =1.0 时，式（14）转变为仅考虑飞行时间的角度优化模型，此时，目标函数存在最优解；同理， a =0 时，式（14）仅考虑油耗，且目标函数存在最优解；

（2） 当 a =0.5 时，式（14）退化为航班飞行时间和油耗两个多目标优化求解问题，此时，目标函数存在一组非劣解集，即Pareto解集；

（3） 当 a ∉{0,0.5,1.0} 时，时间权重和油耗权重不同，式（14）表示以航班总运行成本最小为目标，考虑飞行时间和油耗偏好的角度优化函数.

2.4 约束条件

（1） 角度范围约束. 对于汇聚、分散、转弯3种航路相交结构，其交角范围约束和相互关系约束表示为

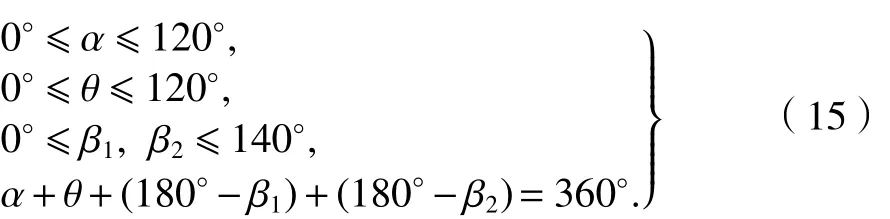
（2） 空域容量约束. 任一时段交叉空域内航班数量不超过该时段空域容量限制.

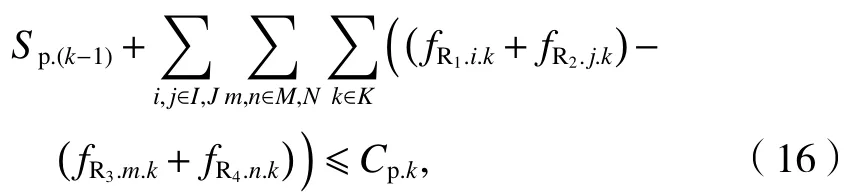
式中： Sp.(k-1)表示k - 1时段滞留在P所在空域内的航班总数量； fR1.i.k( fR2.j.k) 表 示 k 时 段经 R1( R2) 进入交叉空域的交通流； fR3.m.k( fR4.n.k) 表 示 k 时段经R3(R4) 离 开交叉空域的交通流； Cp.k表示 k 时段内交叉点 P 所在空域的容量限制；K表示时段的集合.

（3） 流量守恒约束. 一个航班起终日内，不考虑航班改航情况，由航路 R1、 R2进入交叉空域的总航班数量严格等于从航路 R3、 R4离开该空域的总航班数量，表示为

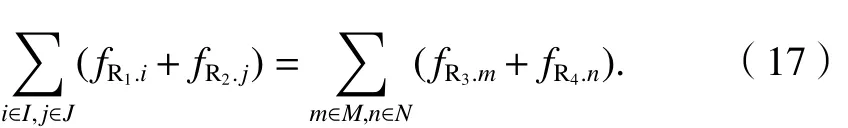
3 实验例证

选取国内某典型交叉航路空域2016年10月和2017年2月两个航班季度内各一个航班计划周期 （7 d） 的数据进行交通量分布统计，近似得到全年数据分布特征；在此基础上利用所提模型优化航路交叉角度，采用带精英策略的非支配排序遗传算法（NSGA-II）进行模型求解[18]，并分析优化结果.

3.1 交通量分布统计

统计两组样本数据中汇聚、分散和转弯结构对应的航班量，计算两组数据的均值和标准差得到结果如表1.

表1 各结构交通量均值和标准差Tab.1 Mean and standard deviation of flight numbers

交通量分布标准差在可接受范围内（＜10），假设其按比例增长，取均值为各结构对应交通分布量，进行模型求解.

3.2 仅考虑时间或油耗优化结果

得到各结构对应交通量，结合式（14），当a=1.0和 a =0 时，分别对应仅考虑飞行时间和仅考虑油耗的情况，求解得到目标函数最优解，即各相交结构对应的最优角度值.

根据所得角度值，设计空域构型，采用与原始结构相同的飞行计划和空域运行规则，进行仿真实验.统计实验结果，得到不同偏好对应的航班总飞行时间、总油耗和总成本如表2.

仅考虑时间时，优化后航班总飞行时间减少13.60%，总油耗增加7.81%，总成本增加0.54%；仅考虑油耗时，优化后航班总油耗减少9.24%，总飞行时间增加9.45%，总成本减小2.89%. 可见，航班飞行时间与油耗成负相关关系，仅考虑一个优化目标，效果较差且很难满足不同空域用户的需求.

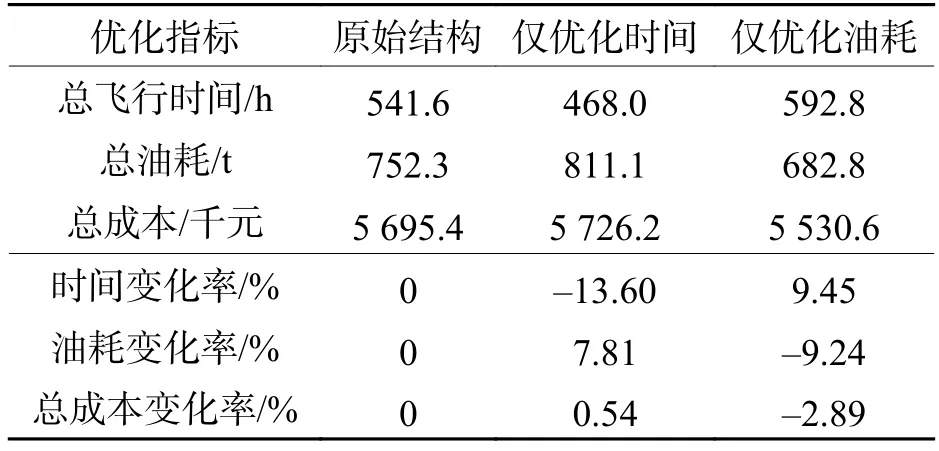
表2 不同偏好对应的优化结果Tab.2 Optimization results for different preferences

3.3 综合考虑时间和油耗优化结果

对飞行时间和油耗无偏好优化，即 a =0.5 时，式（14）退化为两个目标函数飞行时间最小化（式（7））和油耗最小化（式（12））的多目标优化问题，采用NSGA-II算法进行求解. 设置遗传算法初始控制参数：种群规模为100，交叉概率为0.6，变异概率为0.01，终止进化代数为500.

计算完成后，取解集中各结构交角的均值，得到综合优化后各结构对应角度结果如表3.

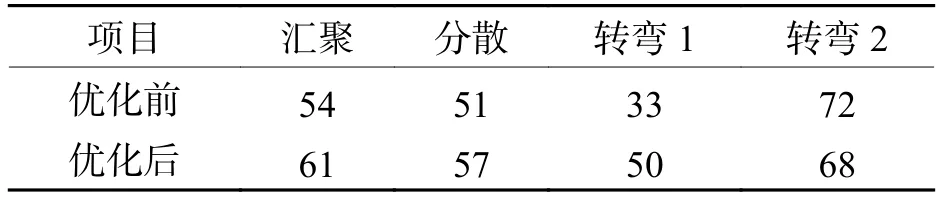
表3 综合优化各结构对应角度Tab.3 Angles of each structure for comprehensive optimization （°）

根据4个角度值，设计仿真实验，得到优化前后航班飞行时间和油耗综合优化结果如表4.

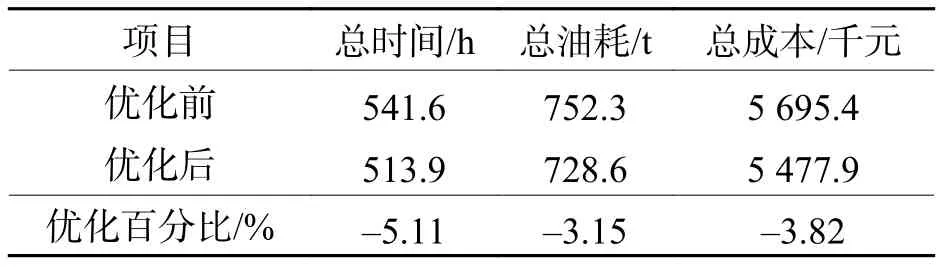
表4 综合优化结果Tab.4 Results of comprehensive optimization

不考虑飞行时间和油耗偏好时，综合优化结果较仅优化飞行时间或仅优化油耗更好；为满足不同空域用户需求，进一步分析带偏好的交叉航路角度优化问题.

3.4 带偏好的角度优化结果

3.4.1 不同偏好优化结果分析

本文将用户偏好量化为权重表示，以0.1为间隔取 a 由0～1.0变化，求解式（14）得到不同权值对应角度最优解集，分别设计空域构型进行仿真实验.分析实验数据可得，总飞行时间和总油耗优化百分比、航班总运行成本如图5.

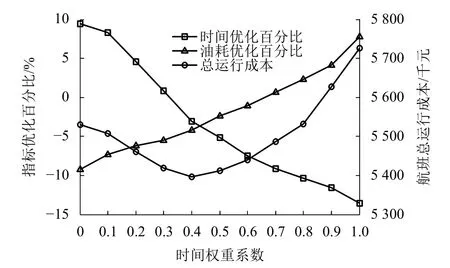
图5 总飞行时间、总油耗、总成本随时间权重变化关系Fig.5 Relationship of total flight time，fuel and cost changes with time weight

随 a 值的增大，总飞行时间逐渐减少，总油耗逐渐增加，总运行成本先减小后增大； a =0.4 时，目标函数取得极小值5 395.8千元.

假设此时空域用户偏好对应的a = 0.4，油耗权重为0.6，根据此权重对应的最优角度值，改进交叉航路结构进行仿真实验. 得到此种偏好下飞行时间结果、油耗结果和其他相关结果，与原始结构航班运行数据对比分析如下.

3.4.2 飞行时间结果分析

图6为优化前后每架航班平均飞行时间对比，可以看出，优化后所有机型平均飞行时间较优化前都有所降低；其中窄体机型（A320、B737）平均飞行时间降低9.89%；宽体机型（除窄体机外）平均飞行时间降低4.57%. 总体来看，优化后仅经过选定交叉航路空域的国内航班，一天节省飞行时间3 038 min，较大程度减少了潜在的飞行延误.

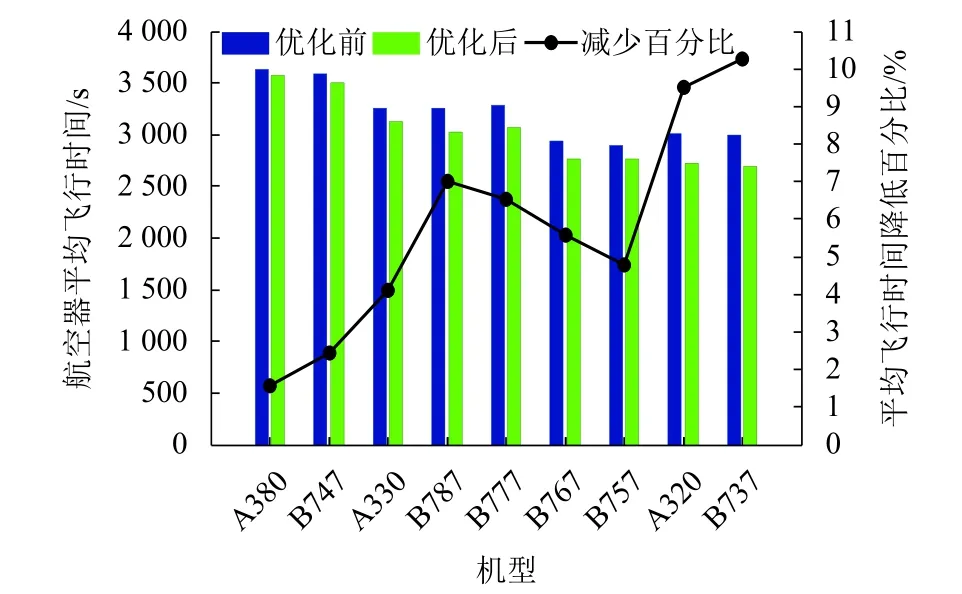
图6 优化前后每架航班平均飞行时间比较Fig.6 Comparison of mean flight time before and after optimization

3.4.3 油耗结果分析

图7为交叉航路空域结构优化前后每架航班平均油耗比较，优化后，窄体机型平均油耗降低8.80%，节省燃油33 613 kg；宽体机型平均油耗降低3.62%，节省燃油2 875 kg.综合来看，交叉航路空域角度结构优化后，仅国内航班一天节省燃油36 488 kg.

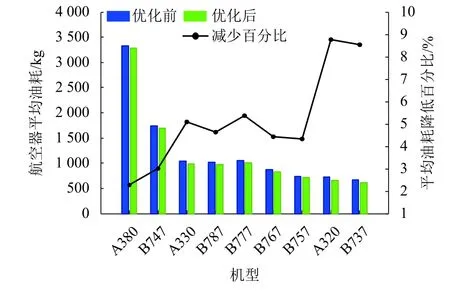
图7 优化前后每架航班平均油耗比较Fig.7 Comparison of mean flight fuel consumption before and after optimization

3.4.4 油耗密度分布结果分析

通过统计分析仿真得到的高维航迹数据（包括经纬度、时间、油耗），从油耗密度（fuel consumption density，FCD）微观角度进一步分析优化前后交叉航路空域内航班的油耗分布特性.

图8为交叉航路原始结构和优化结构对应的燃油密度分布图，其中，每个点代表一个密度单元（0.008 km2）内经过的所有航班油耗总和.

分析优化前后油耗数据得：（1） 优化后平均油耗密度降低20.41%，分析可知优化后汇聚和分散角度更优，交通流在交叉航路运行更趋于畅行态，减少了由于拥堵等原因造成的不必要的燃油消耗；（2） 优化后油耗密度峰值减少74，降幅为26.90%，其原因为航班量相同的情况下，交叉航路结构的优化使得同一密度单元内航班机动飞行（上升、加速、转弯等）减少，从而减少了因机动飞行造成的油耗.

3.4.5 冲突次数和工作负荷分析

前文分析了交叉航路结构优化前后飞行时间和油耗结果，而空域结构改变会影响航班运行安全性和管制工作负荷，因此有必要进一步分析优化前后飞行冲突次数和管制员工作负荷的变化.

图9为优化前后潜在飞行冲突次数随时段分布. 经统计分析，优化后冲突次数峰值降低53.33%，平均冲突次数减少56.12%，空域运行安全性较优化前显著提升.

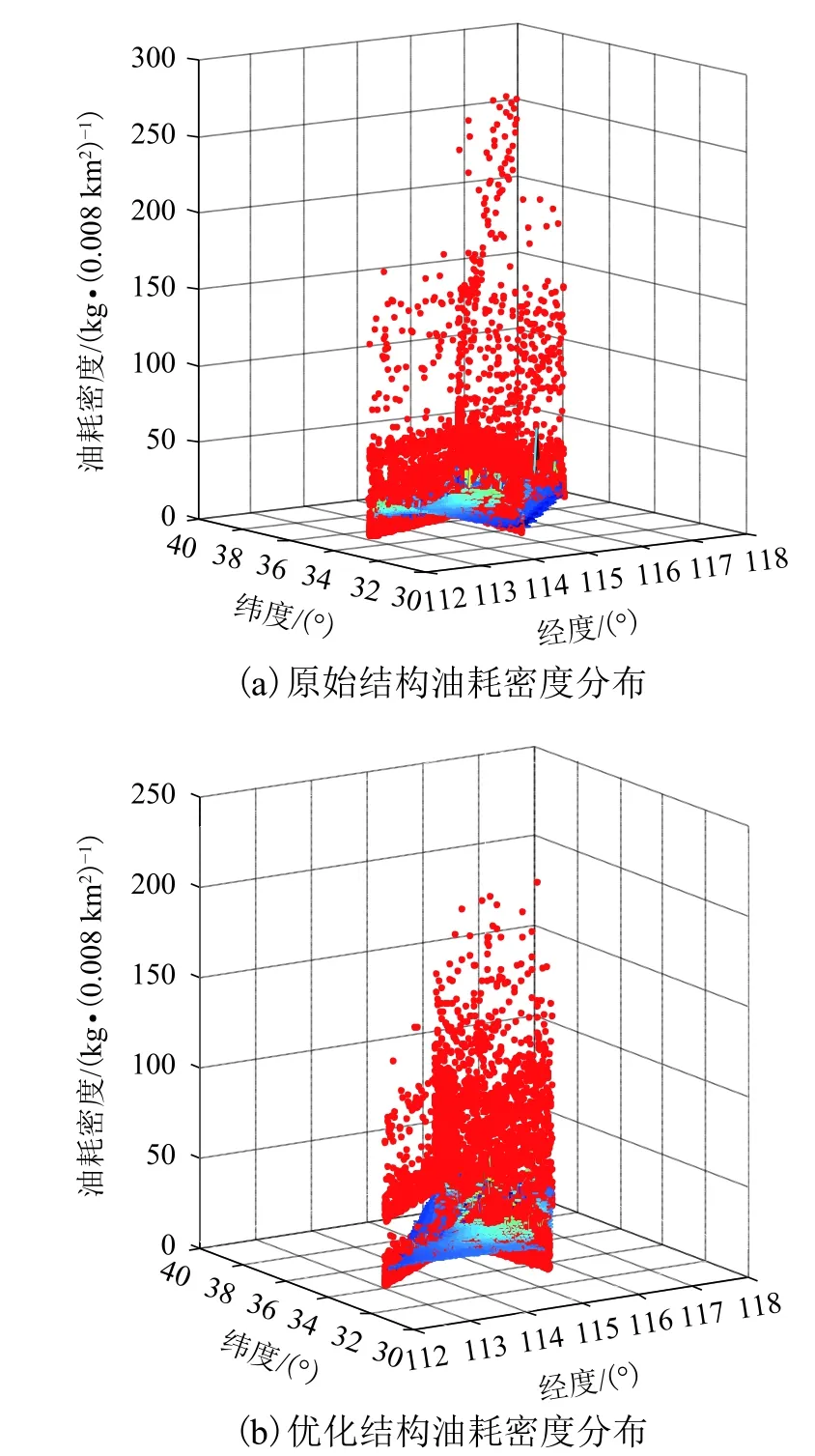
图8 优化前后油耗密度分布对比Fig.8 Comparison of fuel consumption density before and after optimization

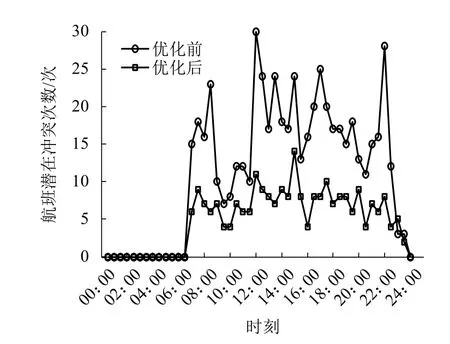
图9 潜在飞行冲突次数Fig.9 Potential flight conflicts

图10 为优化前后管制员工作负荷随时段分布.其中，交叉航路所在扇区内的最大工作负荷阈值和平均工作负荷阈值分别为90和70. 优化前选定扇区内的工作负荷呈现峰值高、均值大的特点，12：00-17：00点时段工作负荷超过扇区最大工作负荷阈值，尤其在11：00-12：00点时段，工作负荷超过阈值19.27%；此外，扇区内平均工作负荷达到阈值的77.54%，趋于饱和. 优化后工作负荷峰值降低45.60%；平均工作负荷降低46.24%. 可见，结构优化对降低交叉航路所属扇区内管制工作负荷效果良好.

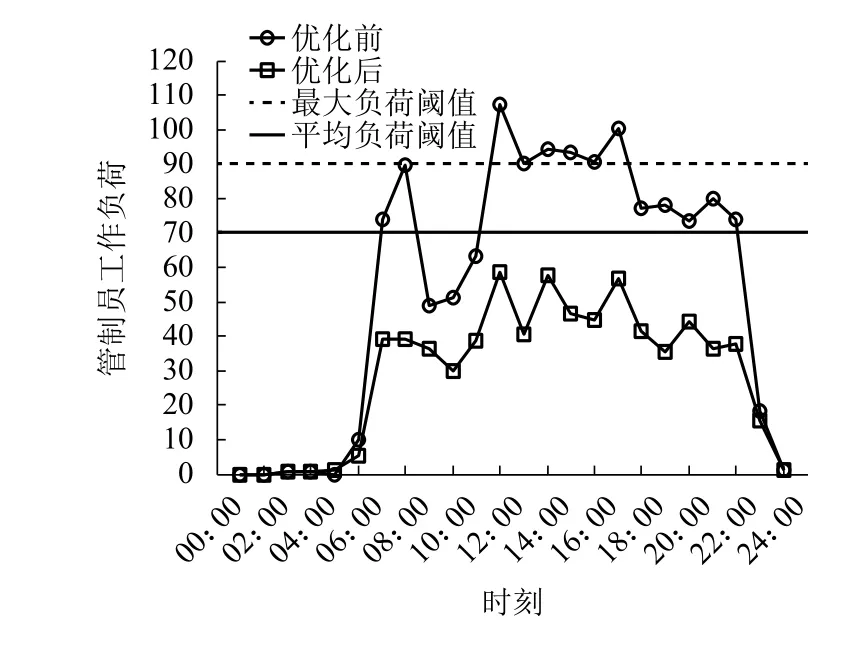
图10 管制员工作负荷Fig.10 Controller workload

3.5 普适性验证

利用本文模型对国内另一交叉航路结构进行优化. 根据模型计算得到的各结构最优角度，建立仿真实验，其中计划数据总包含551个航班，得到综合优化后航班总飞行时间、总油耗和总成本结果如表5所示.

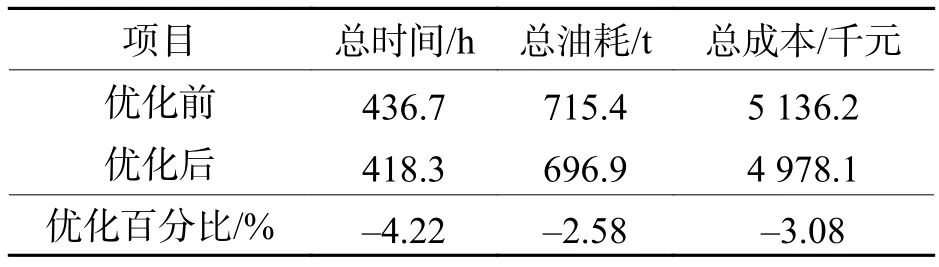
表5 优化前后各评价指标结果Tab.5 Optimization results before and after optimization

优化后航班总飞行时间减少4.22%，总油耗减少2.58%，总运行成本减少3.08%. 可见，本文模型对其他交叉航路结构优化具有良好的普适性. 此外，优化结构对原始空域结构的平均角度扰动仅为11.88%，进一步验证了模型的应用可行性.

4 结 论

（1） 航班飞行时间和航班油耗与航路基本相交结构的角度存在显著的非线性函数关系，基于不同结构对应的交通量分布优化其角度，可从空域资源供给侧提升空中交通运行的质量；

（2） 模型允许决策者在优化交叉航路结构时，通过动态设置权重系数，协调不同空域用户对航班飞行时间和油耗的需求，可为空域规划设计人员优化空域结构提供理论支撑；

（3） 模型在其他交叉航路空域的优化效果同样显著，且优化结构对原始空域结构扰动较小.

本文研究了单向交通流模式下航路交叉角度最优问题，下一步将研究双向交通流模式下多个交叉航路结构之间的全局最优问题.