基于通信网络的直流微网分布式协同控制
杨燕华, 曼苏乐
(上海交通大学 电气工程系,上海 200240)
0 引 言
与交流微网相比,直流微网能够通过减少DC/AC变换过程来降低功率损耗,提高效率,而且不需要考虑同步频率和无功控制[1]。在直流微网中,一些控制策略常用于实现系统性能,如下垂控制[2-3]、协同控制[4-5]。传统的下垂控制很难同时实现精确的功率平衡和较低的电压偏差。而协同控制则通过系统中各个节点间的信息交换来优化控制参数提高系统性能。协同控制通常可以分为集中式控制和分布式控制[6-7]。集中式控制能够提供对整个系统的精确操作和调控,但是通信网络复杂,可靠性低,单个节点的故障会影响到整个系统的稳定性。分布式控制方案的通信网络更简单,系统具有更高的可靠性和可拓展性。
为了提高对直流微网系统的控制性能,考虑通信延时对协同控制性能的影响,本文提出了一种基于通信网络的分布式协同控制方案。
1 系统描述
1.1 微网结构
光伏(PV)发电以直流电压源的形式提供能量,直流负载作为系统中的主要负载,其结构如图1所示。
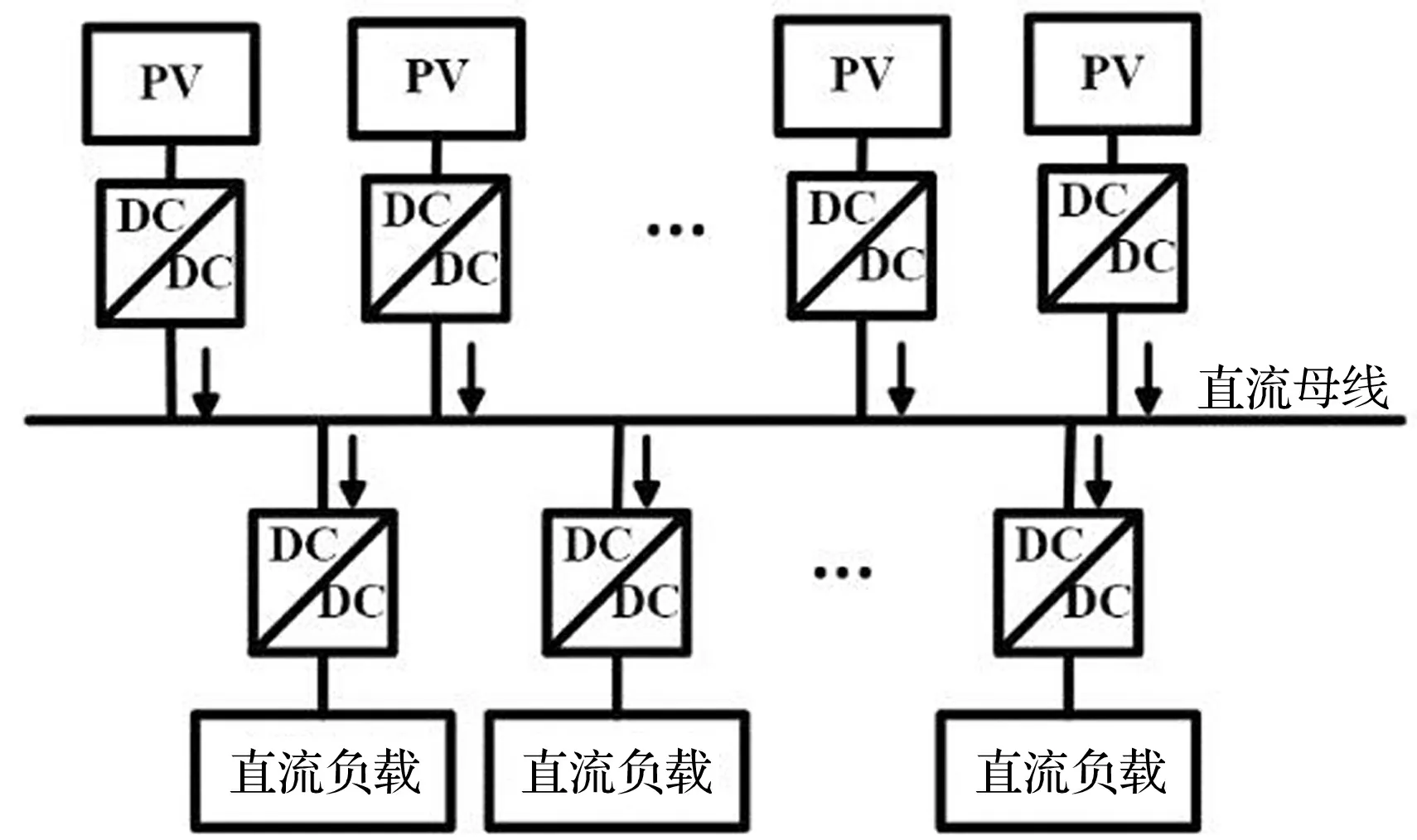
图1 直流微网的结构
DC/DC Buck变换器连接PV发电器与直流母线,并控制直流母线电压。各个节点之间通过通信网络进行信息交换,用于协同控制。
1.2 通信网络
在通信网络中,通信延时的存在必然会影响到系统的稳定性和控制的性能。假设控制器的比特率和传输的数据长度分别为I和L,则每一个节点的最大传输频率fs=I/L。如果通信频率为fc,则对应的通信延时T=1/fc,传递函数Gd如式(1)所示。
(1)
每个节点的平均电压估计值和输出电流值通过通信网络在信道中传输,因此一个数据帧需要8个字节,包括帧头、状态和数据内容。如果控制器的比特率为2 Mbits/s,则数据传输的频率能够达到fs=2×106/(8×8)=31.25 kHz。

图2 通信网络结构
在实际的通信过程中,有很多因素会影响到网络的连通性,比如通信环境和设备故障。考虑通信网络连通的两种极端情况:①网络中所有的链路都连通,即完全连通;②在保证整个网络连通情况下的最坏通信条件,如环形通信结构。在分布式系统中,以4节点为例,完全连通的通信结构和环形通信结构如图2所示。
2 控制方案
2.1 控制方案设计

图3 控制框图
整个控制方案分为两个部分:本地控制器和协同控制器,如图3所示。在本地控制器中采用电流内环-电压外环的双环控制方案。将节点中DC/DC变换器的输出电压与参考电压相比较,得到的电压差值通过P控制器作为电流内环的参考值。再将其电感电流与参考电流相比较,得到的差值通过P控制器进入PWM发生器产生PWM信号用以控制DC/DC变换器。在协同控制器中,各个节点的平均电压估算值以及输出电流值通过通信网络在相邻节点间传输。协同控制器根据接收到的邻节点的平均电压估算值重新计算本节点的估算值,然后与参考电压进行比较得到电压差值。同时根据接收到的电流值得到电流差值,经耦合增益后与上述电压差值相加,通过PI控制器产生一个电压修正量,对本地控制器的参考电压进行优化。与一些常见的控制方案相比,该控制方案仅需要邻节点间的信息传输,能够减小通信延时对系统的影响,同时使系统的结构拥有更好的灵活性和可扩展性。当加入新节点时,只需更新相邻节点的控制器且通信延时保持不变。
2.1.1本地控制器
在本地控制器中,电流内环的参考值Iref为:
Iref=(vref-vout)×kp
(2)
式中:vref和vout分别为参考电压值和变换器的输出电压值;kp为电压外环中P控制器的参数。DC/DC变换器的占空比D为:
(3)
式中:IL为DC变换器的电流值;vdc为DC母线电压值;K为电流内环中的P控制器的参数。
2.1.2协同控制器
协同控制器中,用δvi表示节点i处产生的电压修正量,则节点i优化后的参考电压值及其对应的电压修正量分别为:
(4)
(5)

(6)
δi.pu=∑aij(ij/kj-ii/ki)
(7)
系统的邻接矩阵AG=[aij]∈RN*N,N表示整个系统的节点数。
2.2 小信号模型

图4 Buck电路
在直流微网中,DC/DC变换器是非线性的元件。小信号模型[8]利用数学方法描述DC/DC变换器的工作状态,把各个变量表达为直流分量和交流小信号分量之和,提取交流分量,忽略高次谐波,进行线性化处理。在本文中,采用小信号模型对系统的稳定性和控制器的频率响应进行分析。DC/DC Buck变换器的拓扑结构及其小信号模型结构如图4所示。
2.3 性能分析
系统参数如表1所示。考虑完全连通和环形通信两种结构,以4节点为例,通过小信号模型得到控制系统的带宽,并分析其控制性能。完全连通和环形通信结构的邻接矩阵分别如式(8)和式(9)。
(8)
(9)

当两个相邻节点间的通信频率分别为10 kHz,20 kHz和30 kHz时,其通信延时分别为0.1 ms,0.05 ms和0.033 ms,则对应的vout/vref的带宽如表2所示。在两种通信结构中,控制系统的带宽都在0.7 kHz左右。这表明,该方案在由4节点组成的系统中能够达到预期的控制性能。此外,随着通信频率的增大,通信延时降低,系统的带宽增大。当通信频率相同,在完全连通的通信结构下的系统拥有比环形通信结构下的系统更大的带宽。

表2 不同通信频率下的系统带宽
3 仿真结果
用MATLAB/Simulink仿真一个4节点的直流微网。系统的参数如表1所示。仿真试验共分为3组:①不考虑通信网络,只通过本地控制器对直流微网进行控制;②在完全连通的通信结构下,通过协同控制器一同对直流微网进行控制;③在环形通信结构下,通过协同控制器一同对直流微网进行控制。相邻节点间的通信延时设为0.05 ms,即通信频率为20 kHz。在仿真试验中,相邻节点间传输线的线路阻抗也考虑在内,设为0.05 Ω。输出电流扰动设为100 rad/s,10 A。
在不考虑通信网络,只通过本地控制器实现控制目标的情况下,仿真结果如图5所示。输出电压调节在1.5%(6 V)以内,同时根据输出电流的波形可以得到各个节点之间的功率平衡。采用基于通信网络的分布式协同控制方案对系统进行控制,在完全连通和环形通信结构下的仿真结果分别如图6和图7所示。两种情况下,输出电压的电压调节均在±0.75%(±3 V)以内,响应时间小于0.01 s。通过观察输出电流的波形也可以得到各个节点之间的功率平衡。因此,试验表明,该控制方案能够有效地达到预期的控制目标。

图5 不考虑通信网络的本地控制仿真结果

图6 完全连通的通信网络下的协同控制仿真结果

图7 环形通信网络下的协同控制仿真结果
4 结束语
本文提出一种直流微网的基于通信网络的分布式协同控制方案。整个方案由本地控制器和协同控制器两部分组成。本地控制器采用双环控制方案,电压外环用一个P控制器代替常见方案中的PI控制器和电流反馈的下垂控制环。协同控制器通过相邻节点间的通信产生一个电压修正量优化控制性能。该控制方案降低了控制器的阶数,简化了控制器的结构,电压修正量的算法也减小了通信结构和通信延时对系统性能的影响。最后,仿真试验的结果验证了该控制方案对于系统控制的稳定性以及在电压调节和功率平衡方面的性能。

