基于Simulink的互联电网负荷频率控制仿真研究

陈功贵, 李志军, 郭艳艳, 刘 耀

(1. 重庆邮电大学 重庆市复杂系统与仿生控制重点实验室, 重庆 400065；2. 武汉铁路职业技术学院 机械与电子学院, 湖北 武汉 430205；3. 四川外国语大学 教育学院, 重庆 400031)

频率是衡量电能质量的重要指标之一。在互联电网中,负荷的变化会导致系统频率和联络线功率偏移额定值,从而影响电能的质量和系统的安全。采用负荷频率控制技术(LFC)使各区域频率和联络线功率保持在额定值附近,并且在受到负荷扰动后尽快恢复到稳态[1]。在互联电网负荷频率控制仿真实验研究中,当选取控制器参数后,需要对两区域电力系统施加不同的负荷扰动,以进行电网动态性能仿真验证,并通过改变系统参数进行系统的鲁棒性验证[2]。

Matlab是目前计算机仿真中非常实用的工具,具有功能强大、图形直观等优点。Matlab中的Simulink包含了电力系统仿真工具箱,用户可以直接调用工具箱中的模块搭建互联电网模型,进行负荷频率控制仿真研究。在仿真模型中,可以十分方便地改变系统参数和建立不同的负荷扰动工况进行仿真实验,根据仿真结果分析系统的动态性能和鲁棒性[3-7]。

1 两区域互联电网系统模型

在两区域互联电网中,用合理的假设和近似对系统各元件的数学方程进行线性化,得到原动机、发电机、负荷和调速器等元件的传递函数,再根据各元件的传递函数构建了两区域互联电网的数学模型,如图1所示。

图1 两区域互联电网数学模型框图

在两区域系统中,用区域控制误差(area control error,ACE)来进行调频。其特点是区域内的负荷变动主要由本区内的调频厂来负担,其他区域的调频厂不参与调频,联络线功率维持在计划值[4,8-9]。ACE由频率偏差组成,目标是将区域控制偏差调整为零,表达式如下：

(1)

式中,ACE1、ACE2为区域控制误差。ΔP12、ΔP21为联络线功率偏差,ΔP12=-ΔP21。B1、B2分别为区域1和区域2的频率偏差因子。

实验采用的基本数据如表1所示。

表1 两区系统的基本实验参数

在控制器部分,经典PID控制器的结构和算法简单易懂、容易实现,从而在实际中被广泛应用。本文采用并联PID控制规律,PID控制器由比例、积分、微分3部分组成(见图2)。

图2 PID控制系统原理框图

由PID控制系统原理框图可以得到PID控制器的传递函数,表达式如下：

(2)

式中,Kp、Ki、Kd分别为比例系数、积分系数和微分系数。

如果能够找到合适的PID参数,系统将达到更好的控制效果。本文采用ZN法对PID参数进行整定[10],并对其结果进行适当调整,最终其整定值如下：

Kp=0.755 2,Ki=1.037 6,Kd=1.099 2

(3)

2 两区域互联电网Simulink仿真模块

根据图1的数学模型,在Simulink环境中找到各系统元件的对应模块,各模块的参数设置如表1所示。两区域互联电网仿真模型如图3所示。其中控制系统包括PID控制器和调速器。变量DPL1和DPL2分别表示区域1和区域2的负荷扰动。当电力系统负荷增加(增大DPL1或DPL2),系统频率下降,此时调速器增大汽轮机的阀门开度,增大发电机的输入功率,从而抑制了频率的降低,但调速器只能实现有差调节。当负荷扰动较大时,需要通过负荷频率控制技术实现无差调节,以保证频率偏移和联络线功率维持在规程允许范围内[9-12]。系统仿真模型主要考察区域1的频率偏移Δf1、区域2的频率偏移Δf2和联络线的功率偏移ΔPtie,从而评估系统的动态性能和鲁棒性。

图3 两区域互联电网仿真模型

为了研究的方便,系统中两个区域的参数相同,也将两个区域的PID控制器参数设为相同。PID控制器1的仿真模块如图4所示,参数设置见公式(3)。

图4 PID Control1的仿真模块

3 负荷扰动仿真实验及结果分析

3.1 不同负荷扰动仿真实验

在两区域互联电网仿真模型中,两个区域均有负荷扰动,分别是负荷扰动1、负荷扰动2。在不同的负荷扰动下,对模型进行仿真。Case A表示区域1负荷扰动发生变化的情况。Case B表示区域2负荷扰动发生变化的情况。Case C表示两区域同时发生负荷扰动的情况。不同负荷扰动仿真实验结果见表2。

表2 不同负荷扰动仿真结果

3.1.1 区域1负荷扰动变化(Case A)

区域1的负荷扰动从5%变化到20%,分别进行仿真,其结果如图5所示。随着区域1负荷扰动增加,Δf1、Δf2和ΔPtie的变化趋势大致相同,系统的超调量和调节时间在不断增加。当系统受到较大的负荷扰动时(Case A4),Δf1的调节时间ts=6.038 s,超调量mp=-0.121,稳态误差趋于零。Δf1和Δf2的超调量均为负值,这是由于负荷增加,系统频率会下降。由于区域1的负荷增加,区域2的负荷保持不变,联络线功率从区域2流向区域1,故ΔPtie为负值(规定区域1流向区域2为正方向)。

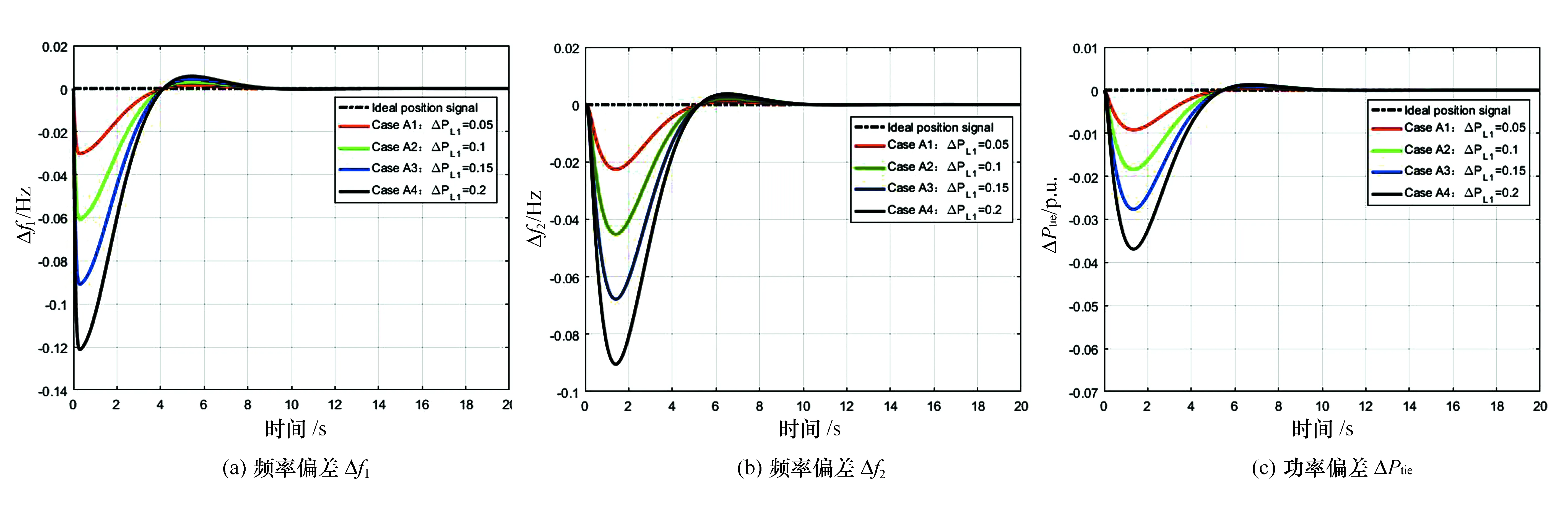
图5 区域1负荷扰动变化的仿真结果

3.1.2 区域2负荷扰动变化(Case B)

系统中只有区域2存在负荷扰动,变量DPL2从5%增加到20%,仿真结果如图6所示。在Case B和Case A情况下,Δf1、Δf2的变化情况相差不大。ΔPtie的超调量为正,因为负荷扰动发生在区域2,联络线功率由区域1流向区域2。

3.1.3 两区域同时发生负荷扰动(Case C)

实际情况中,互联电网的负荷是随时发生变化的。在仿真模型中,区域1和区域2同时施加负荷扰动进行仿真,结果如图7所示。在Case C情况下,Δf1、Δf2和ΔPtie的调节时间大多数要比一个区域发生负荷扰动的调节时间长,最长的调节时间ts=6.931 s。Case C1表示两区域的负荷扰动都为10%,此时Δf1和Δf2的变化情况一样,联络线功率为零。Case C2为区域1的负荷扰动为10%,区域2的负荷扰动为20%。Case C2与Case C1的负荷扰动情况相反。由Case C2与Case C1的对比可知,负荷扰动较大的区域其频率偏差也较大。在Case C2中Δf2和Case C3中Δf1的超调量达到了-0.149,但最终都恢复到零值。仿真结果说明系统能够承受较大的负荷扰动,具有较好的动态性能。

3.2 不同系统参数仿真实验

当区域1存在10%负荷扰动时,系统参数发生变化,对系统进行仿真,研究该系统的鲁棒性。改变汽轮机的时间常数Tt和同步系数T12,其额定值如表1所示,Tt=0.3 s,T12=0.545 pu。在Tt和T12的数值分别变动±50%的情况下进行仿真,Case D表示汽轮机的时间常数Tt变化的情况,Case E表示同步系数T12变化的情况。表3为不同系统参数仿真的实验结果。

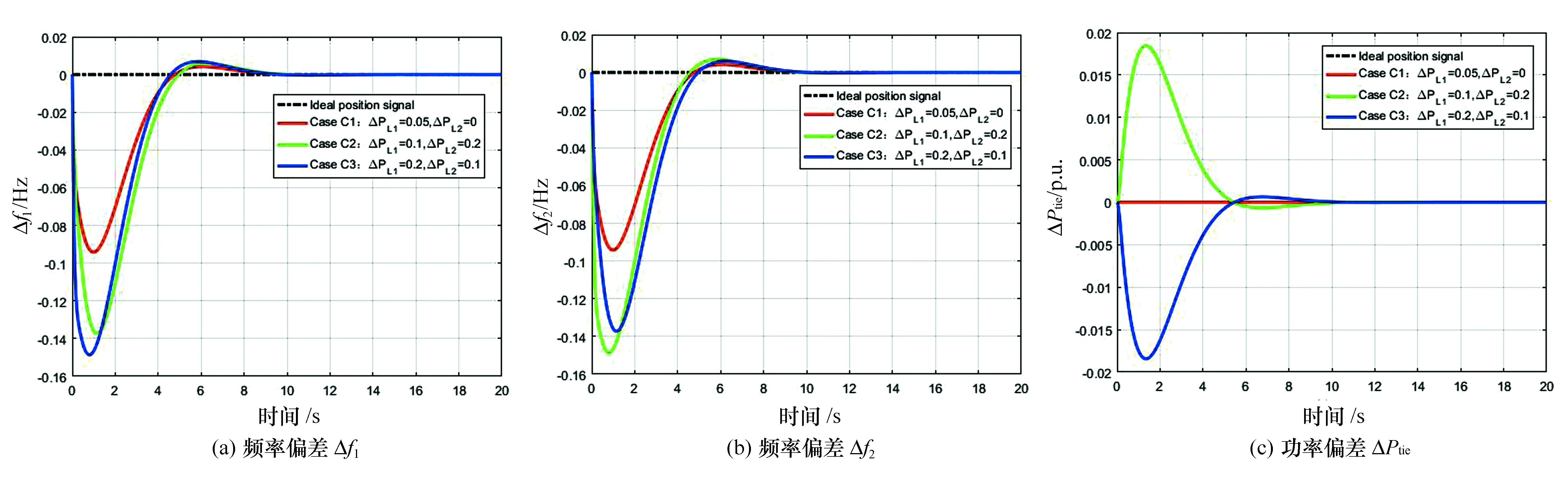
图7 两区域同时发生负荷扰动的仿真结果

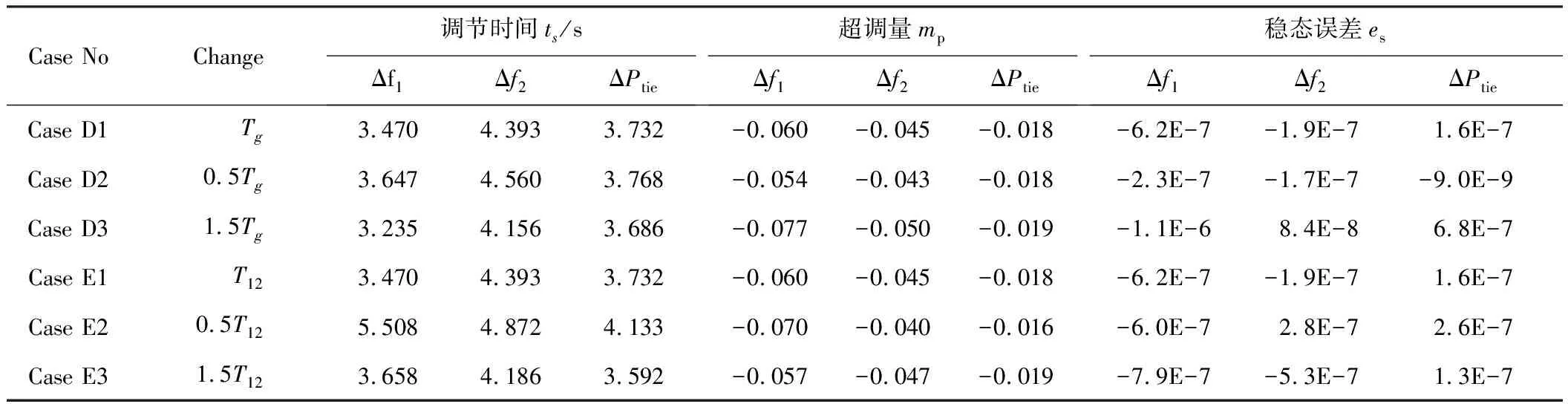
Case NoChange调节时间ts/sΔf1Δf2ΔPtie超调量mpΔf1Δf2ΔPtie稳态误差esΔf1Δf2ΔPtieCase D1Tg3.4704.3933.732-0.060-0.045-0.018-6.2E-7-1.9E-71.6E-7Case D20.5Tg3.6474.5603.768-0.054-0.043-0.018-2.3E-7-1.7E-7-9.0E-9Case D31.5Tg3.2354.1563.686-0.077-0.050-0.019-1.1E-68.4E-86.8E-7Case E1T123.4704.3933.732-0.060-0.045-0.018-6.2E-7-1.9E-71.6E-7Case E20.5T125.5084.8724.133-0.070-0.040-0.016-6.0E-72.8E-72.6E-7Case E31.5T123.6584.1863.592-0.057-0.047-0.019-7.9E-7-5.3E-71.3E-7

3.2.1 汽轮机的时间常数Tt变化(Case D)

如图8所示,当Tt减少50%时(Case D2),系统的超调量略微减小,调节时间小幅度增加。当Tt增加50%时(Case D3),调节时间减少,但超调量略有增加。Tt在一定范围内变化对系统的稳定性影响较小。

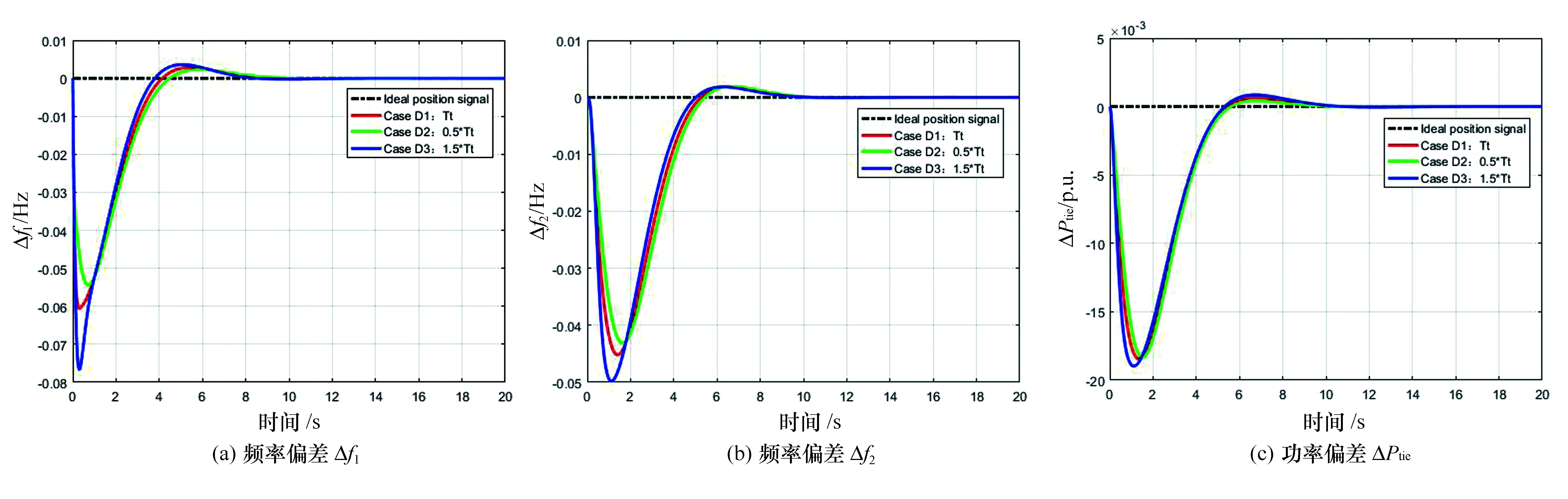
图8 改变Tt数值的仿真结果

3.2.2 同步系数T12变化(Case E)

如图9所示,当T12取值较小时(Case E2),调节时间增加,Δf1的调节时间增加到了5.508 s,Δf1的超调量增加,Δf2和ΔPtie的超调量减小。而当T12取值较大时(Case E3),系统的超调量和调节时间变化很小。仿真结果说明系统参数在一定范围内发生改变,两区互联电网系统仍能保持较好的稳定性,具有良好的鲁棒性。

4 结语

在区域1的10%负荷扰动下,分别改变汽轮机的时间常数和同步系数进行仿真实验,结果表明：不同负荷扰动下系统仍有较好的动态性能,系统参数发生改变时系统仍拥有良好的鲁棒性。将Simulink仿真实验引入课程教学,学生能够将理论知识运用到实践仿真中,激发学生学习兴趣。Simulink实验结果中丰富的仿真图形和数据,使学生对负荷频率控制的动态过程有了充分理解,有助于提高实验教学质量。

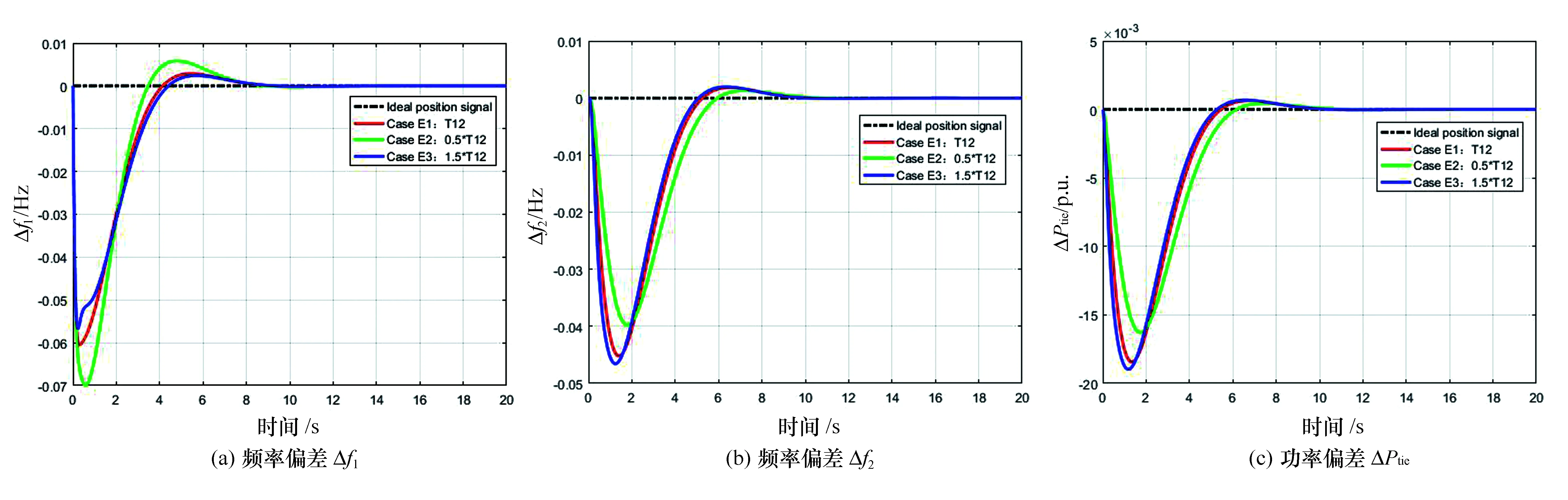
图9 改变T12数值的仿真结果