基于hp-自适应伪谱法的高超声速飞行器上升段闭环制导研究
, ,, ,
(中国兵器工业第203研究所,西安 710065)
0 引言
高超声速飞行器,其速度大于5马赫数,并且通常在20千米到150千米的空间飞行,它是未来军事领域的重要组成部分,它将成为具备战略、战术威慑力的空间作战平台及武器。能够快速有效地击中远程目标,并达到精确打击的目的[1-2]。
文献[3]中Brown等人对于大气段闭环制导的可行性进行了研究,提出了使用真空制导算法得到初始猜想,然后通过增加大气密度的方式求得最优轨迹,并将其作为初始猜想,试验证明这种方法虽然能够较好地提高收敛性能,但依然不能完全保证无法保证一定的收敛特性。如果无法收敛,飞行器的飞行状态始终与最优轨迹误差较大,影响最终精度。
文献[4]使用粒子群算法进行闭环制导研究,通过粒子群算法设计飞行器的飞行轨迹,并在闭环仿真中实时进行迭代。但是这个方法的收敛时间较长,可能无法保证闭环制导的实时性要求。
本文提出一种基于hp-自适应伪谱法的高超声速飞行器上升段闭环制导方法,在飞行器运动动力学模型和约束条件模型的基础上,通过数字仿真验证了其可靠性,文章的研究结果为高超声速飞行器的闭环制导提供了有价值的参考。
1 飞行器上升段建模
1.1 质心运动及动力学方程
飞行器在上升段平面内的运动方程表示为:
(1)
式中,T为推力大小,D为阻力大小,L为升力大小,H为飞行高度,V为飞行器的飞行速度,m为飞行器质量,Isp为燃料比冲,g0为海平面重力加速度,α和θ分别为飞行器的攻角和弹道倾角,q为俯仰角速度[5]。
1.2 气动力模型
选取迎角和马赫数作为影响气动力的最主要因素,拟合公式可以提高算法的快速性,气动力模型如下[6]:
(2)
应用最小二乘法进行气动参数辨识。结果为:
(3)
气动力系数拟合曲线如图1所示。
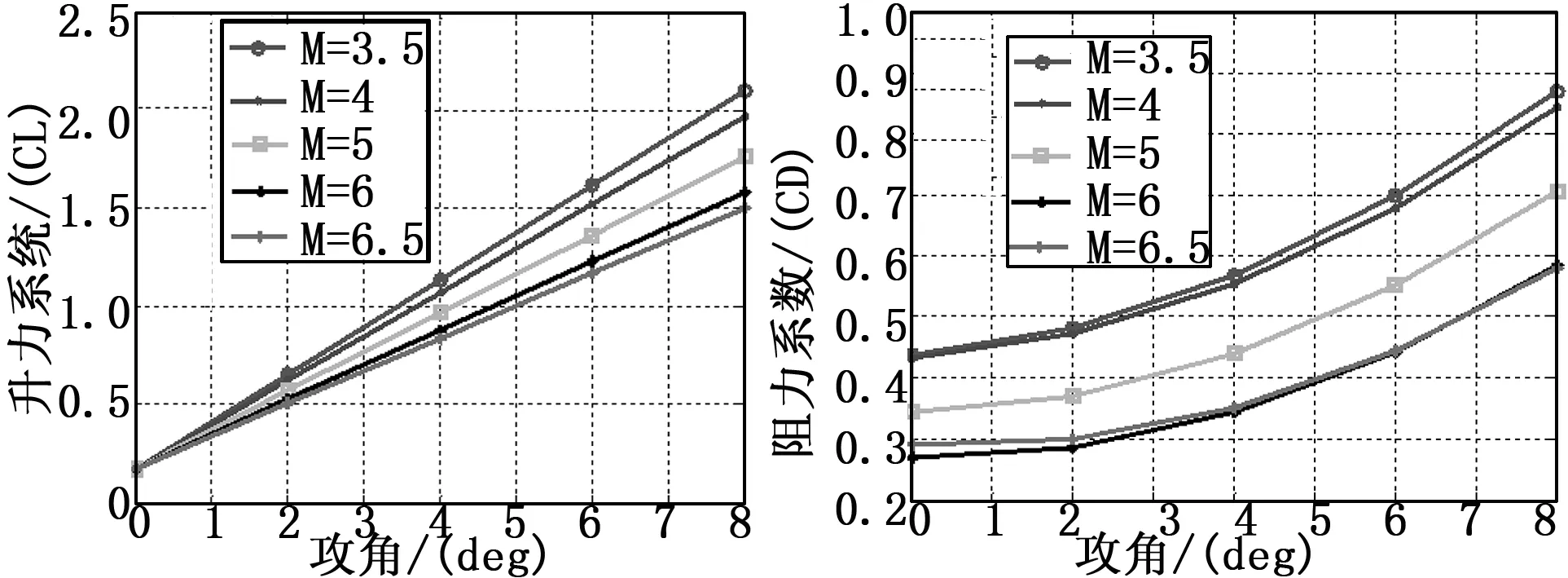
图1 升力系数和阻力系数变化曲线
1.3 发动机推力模型
本文采用涡轮发动机与超燃冲压发动机相结合的推力模型作为研究对象[7]。发动机推力系数CT随着飞行器飞行高度H,马赫数M和攻角α的变化而变化,根据实验所得数据进行曲线拟合,得到推力系数的计算公式:
CT(M,α)=
(4)
2 约束条件
2.1 微分方程约束
高超声速飞行器上升段状态方程的微分约束:

(5)
式中,X(t)是由飞行器上升阶段五个状态量组成的向量,U(t)是攻角控制量α。
X(t)=[H(t),x(t),V(t),θ(t),m(t)]
(6)
U(t)=α(t)
(7)
2.2 状态量和控制量约束
由于飞行器真实舵机等执行机构的限制,在上升过程中,控制能力约束主要反映到可使用攻角的约束,相应的控制量U(t)需要限制在一定范围内[8];据此建立如下约束条件:
(8)
2.3 边值约束
初始边界条件:
H(t0)=H0,V(t0)=V0,θ(t0)=θ0
(9)
终止边界条件:
H(tf)=Hf,V(tf)=Vf,θ(tf)=θf
(10)
其中,t0和tf分别为爬升段的初始时刻和终止时刻。
2.4 路径约束
1)热流约束。
热流密度表达式为:
(11)
式中,
C=7.9686×10-5,N=0.5,K=3.15
(12)
2)动压约束。
飞行器的气动铰链力矩和飞行器表面的耐热材料限制了动压的上限,动压约束的下限值主要与超燃冲压发动机启动的要求相关。
(13)
3)过载约束。
由于本文研究的是高超声速飞行器的上升阶段,所以只分析了其纵向平面,此处过载约束为飞行器的最大法向过载约束,即:
(14)
2.5 目标函数
本文分别选取两种目标函数对基于hp-自适应伪谱法的闭环制导方法进行研究:
(1)为了使高超声速飞行器在巡航阶段能够有充足的燃料进行突防和规避任务,设计飞行器在满足各种约束条件下以最省燃料的方式进行爬升,目标函数则选取为上升段结束后飞行器的质量最大,对应的目标函数为:
minJ=-mf
(15)
(2)为了能够使高超声速飞行器快速有效地完成上升段飞行任务,设计飞行器在满足各种约束条件下以最短时间完成爬升飞行任务,目标函数选取为上升段结束后的时间最小。
minJ=tf
(16)
2.6 上升段飞行走廊
为了更好地描述飞行器飞行包线,基于上节提出的高超声速飞行器在爬升阶段需满足的约束条件,需要保证在飞行过程中的状态变量在动压、过载以及热防护结构所允许的范围之内。通过这些边界条件协同确定了上升阶段的可飞行区域,形成了其飞行走廊,以便于对其飞行区域进行划分。

图2 上升段飞行走廊
3 hp-自适应伪谱法算法设计
3.1 飞行轨迹规划策略
高超声速飞行器上升段的闭环制导研究是非线性问题,一般的非线性最优控制问题的标准形式为Bolza型问题[10],其最优控制模型可以表示为:
(17)
(18)
e(x(t0),t0,x(tf),tf)=0
(19)
c(x(t),u(t),t)≤0
(20)
在上面的公式中,x∈Rn为状态变量,u∈Rm为控制变量,t为任意时刻,t0为初始时刻,tf为终止时刻。Φ表示Mayer型代价函数,g表示Lagrance型代价函数。
结合本文所研究的高超声速飞行器闭环制导研究问题,将基于飞行器最省燃料和最短飞行时间两种目标函数的轨迹优化问题转化为最优控制问题,如下式所示。
(1)最省燃料最优控制问题:
minJ=-mf
(2)最短飞行时间最优控制问题:
minJ=tf
3.2 最优控制问题的离散化
如果要对上述连续的Bolza最优控制问题采用直接法进行求解,首先需要对连续最优控制问题进行离散化[11],将其转化为有限维度的代数问题,本文将采用基于插值多项式近似逼近状态量和控制量的方法。
高超声速飞行器的轨迹优化问题即为能够达到最优性能指标的最优飞行轨迹。在进行轨迹优化时需要将优化问题转化为一般形式的最优控制问题,接着按照上一节的计算方法对标准形式的轨迹优化问题进行离散化;最终得到关于本文所研究内容的离散形式如下。
以高超声速飞行器上升段最省燃料问题为例:
(1)最优性能指标函数离散后的表达式:
(21)
(2)动力学微分方程离散化表达式:

(22)
(3)边值约束离散化:
E(X0,t0,Xf,tf)=0
(23)
(4)路径约束、状态量和控制量约束。
离散化表达式:
(24)
其中,状态变量Xi=[hi,Vi,θi,mi],控制量Ui=[αi]。
为了将离散后的结果更加具体化,结合本文的研究内容,将运动方程离散化形式表示入下:
⟹
(25)
3.3 hp-自适应伪谱法算法流程
hp自适应策略即是求解连续最优控制问题时,对相应问题进行单元划分,每个单元再运用伪谱法进行离散近似和参数化,同时所分单元的数目和每个单元近似用的多项式的阶数即配点数,采用一种自适应的策略来获得。hp-自适应伪谱法其实就是综合了h方法和p方法,首先将时间分段,然后对每一段继续采用Guass伪谱法进行离散化。
基于以上分析计算,可以进一步得到hp-自适应伪谱法的迭代流程图和制导系统流程图。

图3 hp-自适应伪谱法流程框图

图4 制导系统流程图
4 闭环制导策略
如图5所示,为飞行器整个飞行阶段的闭环制导轨迹示意图。整个阶段根据设计策略分为n个优化时间段,在每一个时间段内实时运行伪谱算法,根据惯性导航装置测量的飞行器当前姿态和位置信息生成最优轨迹,将计算得出的控制量转化为舵机装置的输出电压,舵机偏转控制导弹按照设计出的最优轨迹飞行。在这个阶段中,飞行器会由于外界干扰因素而偏离最优轨迹,在一个解算周期内到达如图所示的A点。
当飞行器在一个解算周期后到达图中A点,飞行控制器根据测量元件输出的飞行器当前的飞行状态,继续生成控制指令,导引飞行器按照方案弹道飞行。整个飞行阶段划分为多个解算周期,直至到达目标位置,满足约束条件。

图5 闭环制导原理示意图
5 仿真验证
5.1 仿真条件设置
飞行器初始高度和初始速度:
(26)
终端高度和终端速度:
(27)
路径约束参数如表1所示。

表1 路径约束条件
5.2 最优轨迹优化
基于飞行器模型参数和约束条件,本节对高超声速飞行器上升段最省燃料和最短飞行时间轨迹进行优化验证,精度要求设置为10-4。
(1)最省燃料最优轨迹,如图6所示。

图6 高度、速度、过载、质量变化对比曲线
(2)最短飞行时间最优轨迹,如图7所示。

图7 高度、速度、过载、质量变化对比曲线
从仿真结果可以分析出:
1)最省燃料最优轨迹中,飞行器高度在大约100米时下降了一段距离,这是由于此时速度达到了4马赫,超燃冲压发动机准备开始工作,由于高度继续下降不会导致速度的减小,所以为了使终端燃料最多,优化策略在保证完成终端目标的情况下使飞行器高度有所下降。其他参数均满足约束条件。
飞行器的总飞行时长为234.65 s。
2)最短飞行时间轨迹优化中,飞行器完终端目标总时间为205.41 s,满足了快速性要求,其他参数均满足约束条件。
5.3 闭环制导仿真验证
为了更好地验证闭环制导策略的优点,采用开环制导方式制导进行比较,以优化飞行器最短飞行时间作为仿真条件。
(1)开环制导。
所谓开环制导,即整个飞行阶段不考虑外界干扰因素的影响,在飞行器上升段初始时刻就优化出一条最优轨迹,飞行过程中以该弹道作为方案弹道的制导方式。
(2)闭环制导。
在整个飞行过程中,共分为多个解算周期,每一个解算周期的初始时刻会获取测量元件输出的飞行器状态信息,根据该信息和终端目标信息实时在一个周期内生成一条最优轨迹。
仿真曲线说明如下:点划线为闭环制导最优曲线;虚线为闭环制导飞行器飞行实际曲线;点线为开环制导飞行器飞行曲线;实线为上升段初始时刻优化出的最优曲线。
以升力系数拉偏为例,对本文提出的闭环制导策略进行验证,右侧的示意图中的两条曲线表示的是开环制导和闭环制导与理想闭环最优轨迹参数的误差。
对升力系数拉偏+10%情况进行分析。仿真结果如下图所示。

图8 高度变化对比曲线
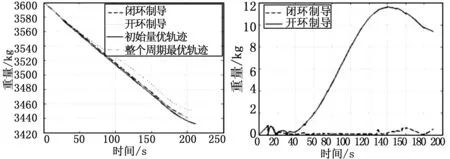
图10 质量变化对比曲线

图11 动压变化对比曲线
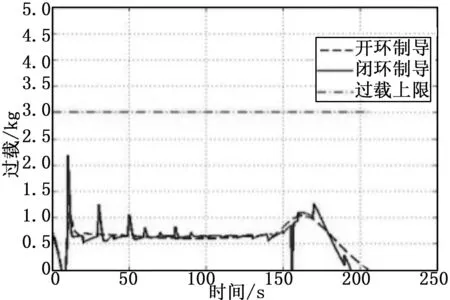
图13 过载变化对比曲线
仿真结论:
(1)开环制导方式下,飞行器终端高度与理想终端高度偏差约260 m,且飞行过程变化剧烈;闭环制导方式下飞行器高度误差约为10 m;
(2)从速度变化曲线可以看出,开环制导方式下的速度与终端任务速度偏差较大,约100 m/s,而闭环制导方式下的偏差为20 m/s。
(3)从质量变化曲线可以看出,开环制导和闭环制导方式下变化趋势大致相同;
(4)由图9至图11可以看出,对于飞行过程的路径约束,闭环制导方式下飞行动压、热流密度和飞行过载均满足约束条件;开环制导方式下动压在某一阶段超过了上限值,存在风险;由于飞行器每一个周期内都会重新优化一次飞行轨迹,所以过载变化较剧烈,但仍然满足约束条件。
(5)从整个阶段的飞行时间来看,闭环制导方式下的飞行时间优于开环制导;
(6)本文的仿真验证是在普通PC机上进行,每个周期的闭环仿真计算时间大约为1.2 s,优于绝大部分智能算法。
6 结论
文章通过分析高超声速飞行器上升段的飞行状态,提出一种基于hp-自适应伪谱法的闭环制导策略,并建立了飞行器上升段的运动模型及约束条件模型,将最优控制问题中的变量离散化,将存在约束的最优控制问题转换为非线性规划问题;同时完成开环制导和闭环制导数字仿真对比验证。
仿真结果表明,文章研究的基于hp-自适应伪谱算法闭环制导策略可以根据飞行器当前状态量在一定的解算周期内实时在线设计最优飞行轨迹,消除某些外界因素对飞行器轨迹造成的偏差,最终以我们期望的最优条件和最优速度到达期望的终端目标位置。同时,该算法收敛时间快,具备闭环制导在线快速优化的潜力。

