牵引供电系统低频振荡抑制分析

杨 杰，胡海涛，周 毅，陶海东，赵朝蓬，何正友



牵引供电系统低频振荡抑制分析

杨 杰，胡海涛，周 毅，陶海东，赵朝蓬，何正友

针对徐州铁路枢纽牵引供电系统中网压低频振荡问题，总结了低频振荡网压网流波形规律，建立了相应的HXD2B型机车的频域阻抗模型及车网闭环系统传递函数模型，利用零极点判据揭示了低频振荡的机理和系统参数对低频振荡的影响规律；讨论了4种网压低频振荡抑制方案的可行性，最终确定采用扩容牵引变电所主变压器的技术方案，并给出了详细的容量选取方法。经测试该方案能有效解决低频振荡问题，具有推广应用价值。

低频振荡；频域阻抗模型；牵引变压器；抑制方案

0 引言

随着我国高速铁路与重载铁路运输的快速发展，一系列大功率交直交型动车组和电力机车（以下简称机车）投入运行，极大地提高了我国铁路高速、重载运输能力。与此同时，交直交机车的密集开行导致牵引供电系统接触网网压低频振荡（以下简称低频振荡）问题频发，引发网压大幅波动，严重时触发机车保护造成牵引闭锁。2008年1月2日，大秦线湖东站多台HXD1型电力机车整备导致低频振荡，机车牵引封锁无法正常出入库[1]；2010年，CRH5型动车组在北京、沈阳和青岛等地多次引发低频振荡导致动车组晚点[2]；2011年11月，哈机库内HXD3B、HXD3C型电力机车库内整备导致低频振荡，影响机车工作[3]；2016年一年中，徐州枢纽发生了158起低频振荡事故，严重影响了徐州枢纽的正常运输秩序[4]。由此看出，低频振荡是铁路运输中普遍性问题，且影响严重。在国内所有电气化铁路低频振荡问题中，徐州枢纽低频振荡问题最为典型。徐州枢纽位于京沪、陇海（郑徐）2大铁路干线的交汇处，是我国最繁忙的铁路枢纽之一。徐州枢纽低频振荡问题十分严重且持续多年，一直未能彻底解决，2011—2016年间，低频振荡月平均次数最高达50次之多，平均最低波动电压达7412.8V，严重影响了列车的正常运行[5]。因此，解决徐州枢纽低频振荡问题对破解我国电气化铁路牵引供电系统低频振荡问题具有重要意义。

低频振荡多发生于多台机车同时升弓整备的工况，随着整备机车数量增多，网压波动更为剧烈。低频振荡发生时，牵引变电所主变压器声响异常，机车不能正常取流。文献[6]对基于控制下的机车建立了对应车网系统小信号模型，提出了车网系统低频振荡欠阻尼机理，详细分析了车网系统建模过程，并得出影响车网系统低频振荡的因素；文献[7]利用VSC频域阻抗建模方法，建立了轴下车网阻抗模型，分析机车数量和机车控制参数对车网系统低频振荡现象的影响规律，总结了低频振荡发生时在低频段机车阻抗的变化规律，给出了调节控制参数抑制低频振荡的最优顺序；文献[8]针对轴下多输入多输出系统，提出基于静止域的车网稳定性分析判据，较单值稳定性判据适用范围更广，效果更明显。上述研究详细分析了基于轴控制的机车引起的系统低频振荡，但是未分析基于瞬态电流控制策略的机车引发的低频振荡。文献[9]对HXD2B型机车采用阻抗分析法研究了系统低频振荡的产生机理与影响因素，搭建了详细的车网系统仿真模型，并利用该模型对低频振荡影响因素进行仿真分析，但其机车阻抗模型未分析电压环控制对车网系统的影响，存在一定局限性。

本文针对徐州铁路枢纽牵引供电系统低频振荡问题，基于阻抗分析法，建立HXD2B型机车双闭环控制下的频域阻抗模型，分析车网系统闭环传递函数，揭示低频振荡产生的原因以及参数影响规律。为了彻底解决低频振荡问题，本文提出扩容牵引变电所主变压器的技术方案，并通过现场测试对该方案的效果进行验证。

1 徐州铁路枢纽低频振荡现状

2016年1月，课题组对徐州枢纽低频振荡问题进行了测试实验。在升弓整备8台机车的测试中检测到网压异常波动，徐州北变电所电压峰值最高达49672.2V，最低达18476V，严重偏离正常数值范围。典型波形如图1和图2所示。

图1 系统低频振荡时变电所馈线网压网流波形

图2 系统低频振荡时机车输入侧网压网流波形

结合现场测试数据和文献[5]可得出低频振荡的特征：（1）网压网流的波动具有同步性，网压稳定时，网侧电流也稳定；（2）网压异常波动时，机车、开闭所、牵引变电所处均能检测到波动的电压和电流；（3）接触网上存在10Hz以内的网压网流波动，且低频振荡频率不固定；（4）网压网流波形放大后未出现明显畸变，因此网压低频振荡与车网系统低频不稳定有关；（5）机务段内可以稳定升弓整备的机车数量在7台以内。

2 车网系统建模与低频振荡机理

2.1 牵引供电系统建模

牵引供电系统主要由牵引变电所和接触网组成。牵引变电所内主变压器将电力系统110kV电压降为27.5kV，电流通过接触网传送至机车，再经过钢轨回流至牵引变电所，构成回路。根据戴维南等效电路可知，牵引供电系统可等效为电压源与牵引供电系统等效阻抗串联，如图3所示。

图3 牵引供电系统等效电路

徐州枢纽的供电方式为带回流线的直接供电方式。徐州北变电所主变压器（以下简称主变压器）为非阻抗匹配平衡变压器，其容量为31.5MV·A，额定电压为110/27.5kV，额定电流为165.3/572.7A。档位为I档，即11550/27.5kV（高压侧额定电压最高档）时，高压侧额定电流为157.5/572.7A，短路电压百分值10.54%，额定铜耗为160kW。

设主变压器额定铜耗为k(kW)，额定容量为T(MV·A)，变压器短路电压百分值为d%，主变压器原边Y接相阻抗归算到27.5kV侧等效D接相阻抗表达式[10]为

将主变压器参数代入式（1）可得变压器的等效电阻、电抗分别为

0.37W（2）

设牵引变电所出线接触网长度为，单位长度接触网等效阻抗为Ð。由现场资料知，徐州北牵引变电所到机务段的接触网长度= 7 km，接触网每公里等效阻抗Ð约为0.43Ð68.20°W，考虑复线情况下接触网等效电阻与电抗分别为

由于外部电力系统电压等级高，电压稳定，其对于主变压器的输入阻抗可忽略不计，因此牵引供电系统等效阻抗为

2.2 HXD2B机车建模

机务段测试的车型主要为HXD2B型电力机车，该车整流器采用瞬态直接电流控制策略，其控制框图如图4所示[11]。

图4 瞬态直接电流控制框图

设N为整流器控制系统输入信号，N为系统输出信号，对系统信号进行拉普拉斯变换，并将PWM模块利用延时环节等效，可得整流器系统线性化后复频域传递函数模型，即整流器输入导纳r()。设机车整备工况下工作的整流器数量为r，机车牵引变压器变比为，则在机车牵引变压器一次侧机车的输入导纳为

由于机车在整备工况下只有辅助电路工作，功率较小，负载电流可忽略。

根据整流器控制框图可得整流器输入导纳的传递函数为（G()由G表示）

则1台机车的输入导纳为

由文献[14]可知，机车升弓整备时主电路6套整流器中有4套由于辅助电路运行而处于工作状态，因此r= 4。

图5 整流器控制框图

对于多车-网闭合系统，根据其电路拓扑可得车网系统传递函数框图如图6所示。N为牵引供电系统电源电压，pcc为机车输入电压，S()为牵引供电系统等效阻抗，Z为牵引供电系统等效阻抗上的电压降。

图6 车网系统传递函数框图

由图6可知，车网系统传递函数为

2.3 车网系统低频振荡机理

在车网系统中，变电所等效电压源是稳定的，因此系统的稳定性取决于系统传递函数零极点的分布，如果系统的极点出现在复平面的右侧则系统不稳定。通过分析车网系统传递函数模型可知，车网系统低频振荡是由于系统中机车和牵引网参数不匹配导致车网系统传递函数出现位于复平面右侧的低频极点，造成车网系统出现低频振荡。

3 车网系统参数对稳定性影响规律

分析系统参数对系统稳定性影响时，使用基准参数如表1所示。

表1 车网系统基准参数

3.1 机车数量

在车网系统基准参数下，改变整备机车数量，闭环系统的主导极点如图7所示。随着接入机车数量的增加，车网闭环系统传递函数主导极点向复平面右侧移动，系统趋于不稳定，系统振荡频率降低。根据图7可知，系统振荡频率为5.8Hz，在实际低频振荡范围内；在基准参数下，系统能稳定整备的机车数量为8台左右，与徐州北变电所实际能稳定接入7台整备机车有1台误差，因此模型可用于分析徐州枢纽低频振荡问题。

图7 机车数量对系统稳定性影响

3.2 电压环参数

在基准参数下，将模型中电压环积分参数VI由0.97增加到8.73。在极点图中，VI在0.97-1.7时对应的主导极点位于左半平面实轴上，系统稳定。在图8中，VI由1.7增加到8.73时，车网闭环系统的主导极点向复平面右侧移动，系统趋于不稳定，VI的临界参数为4.12，系统可能的振荡频率为6 Hz左右。当VP从0.1增大到0.9时，系统主导极点分布显示，系统先趋于稳定后趋于不稳定，VP的稳定区间在0.45～0.77，系统可能的振荡频率在3.5～7.8Hz，且随着VP的增大而增大。因此在基准参数下，系统发生低频振荡时，减小VI参数；当振荡频率大于6Hz，减小VP参数；当振荡频率小于6Hz，增大VP参数可抑制系统低频振荡。

图8 电压环参数对系统稳定性影响

3.3 电流环参数

机车电流环用于使机车电流快速跟踪给定电流，可控参数为电流环比例参数IP。将IP从0.028逐渐增大到0.25，由图9可知，系统主导极点向复平面左半平面偏移，系统趋于稳定，系统振荡频率增大，在基准参数下，IP的临界值为0.13。因此，增大IP可抑制系统低频振荡。

3.4 牵引供电系统参数

牵引供电系统等效阻抗由接触网等效阻抗和变电所主变压器等效阻抗组成。在基准参数下，当s从0.18W增大到1.66W时，由图10可知，主导极点随s增大向右半平面移动，振荡频率降低，系统趋于不稳定。由于主导极点集中在复平面左侧，系统稳定性未发生明显变化，因此系统稳定性对s变化不敏感。当s从5.6mH增大到50mH时，系统主导极点由复平面左侧向右侧移动，系统趋于不稳定。s的临界值在32mH，振荡频率在5.8Hz左右。系统稳定性对s的变化更敏感，减小网侧等效电感可有效抑制系统低频振荡。

图9 电流环参数对系统稳定性影响

图10 牵引供电系统参数对系统稳定性影响

4 车网系统低频振荡抑制方案

对车网系统低频振荡的抑制方案目前有4类：（1）修改机车参数方案，根据上文分析机车参数会影响车网系统的稳定性，适当调节控制系统参数可抑制系统中低频振荡；（2）修改机车控制方案，避免机车整备时整流器受控制系统影响，从源头上解决低频振荡问题；（3）增加设备方案，增设补偿设备可以增强系统抑制振荡的能力；（4）供电侧治理方案，适当减小牵引供电系统阻抗可抑制系统低频振荡。

4.1 修改机车参数方案

机车控制参数的改变会影响车网系统零极点的分布，因此修改机车参数可抑制车网系统低频振荡。在基准参数下，增大IP、减小VI、根据振荡频率改变VP均可抑制系统低频振荡。搭建车网系统仿真模型，以修改电流环参数为例，仿真波形如图11所示，1s前为低频振荡下网压网流波形，1s后为增大电流环控制参数下网压网流波形，通过对比可看出系统低频振荡得到抑制。

图11 增大电流环参数后仿真波形

在实践中发现，由于机车控制系统复杂，单纯修改机车参数并不能彻底解决车网系统低频振荡问题。机车控制参数在机车出厂前经过大量严格的试验验证，满足系统快速性、稳定性等多方面指标，可供修改的参数范围较窄。参数调节需要建立相关车型的数学模型，并修改其参数，工作量较大。在2014年徐州枢纽发生低频振荡问题最为严重的时期，曾通过修改机车参数的方法缓解了低频振荡问题，但仍未能彻底解决[4]。因此，修改机车参数的方案具有较大局限性。

4.2 修改机车控制方案

当系统发生低频振荡时，控制机车使整流器IGBT封锁，利用反并联二极管组成的不控整流电路向辅助电路供电，此时机车呈现无源特性，不受控制系统影响，不会引发系统低频振荡。仿真波形如图12所示，1s前为低频振荡下网压网流波形，1s后为切换机车控制方案后网压网流波形，通过对比可看出1 s后系统低频振荡消失。该方案可以消除系统低频振荡，但需改变机车现有控制程序，需在进行机车设计时做出调整，既有系统中不易实现。

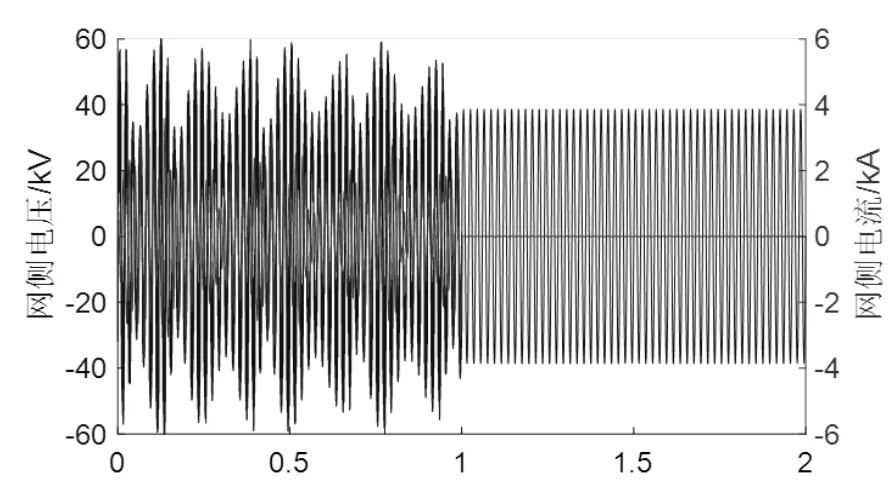
时间/s

4.3 增加设备方案

文献[15]中提到可以根据电力系统稳定器PSS（Power System Stabilizer）的原理在机车上加装功率振荡抑制器POD（Power Oscillation Damper）来抑制系统低频振荡。抑制器需要实时计算系统的有功、无功功率，其精度要求较高。若无法满足相应精度要求，易导致系统不稳定。根据对现场的了解，徐州枢纽曾加装静止无功补偿SVC(G)、DVR等装置，但抑制振荡效果并不理想。因此加装设备方案不能稳定有效地抑制系统低频振荡。

4.4 供电侧治理方案

4.4.1 网侧阻抗占比分析

根据以上分析可知，徐州枢纽牵引供电系统中主变压器阻抗和接触网阻抗占比如表2所示。

表2 牵引供电系统阻抗占比统计

由表2可知，牵引供电系统总阻抗中电抗分量占比较大，且总电抗中主变压器电抗占比最大。因此为了有效削减牵引供电系统阻抗，根据式（1）可知需要提高变压器容量。

4.4.2 主变压器容量对系统稳定性影响规律

根据变压器等效阻抗计算式可知，变压器等效阻抗与变压器容量关系密切，增加变压器容量可以同时减小变压器等效电阻和电抗。假设主变压器额定铜耗和短路电压百分值不变，将变压器容量从6.3MV·A提高到56.7MV·A，根据系统传递函数可得闭环系统的主导极点分布情况如图13所示，可以看出，随着主变压器容量增加，主导极点向复平面的左半平面移动，系统趋于稳定，振荡频率增加。

图13 主变压器容量对系统稳定性影响

由于主导极点实部的正负决定了系统此时的稳定性，因此以主变压器容量标幺值为横坐标，主导极点实部为纵坐标，可得极点实部变化情况如图14所示。可以看出，主导极点实部随主变压器容量增加变化越来越小，即主变压器容量较大时系统稳定性对变压器容量敏感度降低。因此并非主变压器容量越大越好，考虑经济性，需要根据实际需求确定容量。

图14 变压器容量对主导极点影响

4.4.3 主变压器参数选择

由上述分析可知，增大主变压器容量可以提高车网系统稳定性。铁标规定变电所主变压器的额定容量宜从31.5、40、50、63、75MV·A及更高值中选择，110kV级变压器的短路电压百分值一般为8.4%或10.5%[16]。由于主变压器等效电抗的大小对系统稳定性影响更大，根据式（1）可知，扩容后主变压器短路电压百分值应选择8.4%。假定主变压器额定铜耗仍为160kW，短路电压百分值为8.4%，主变压器容量分别为40、50、63、75MV·A时，10～21台机车整备时车网系统主导极点分布如图15所示。由主导极点分布结果可知，增加主变压器容量可提高供电系统机车最大容纳数量（下文简称“机车容纳量”），系统机车容纳量均在10台以上，较好地抑制了系统低频振荡。

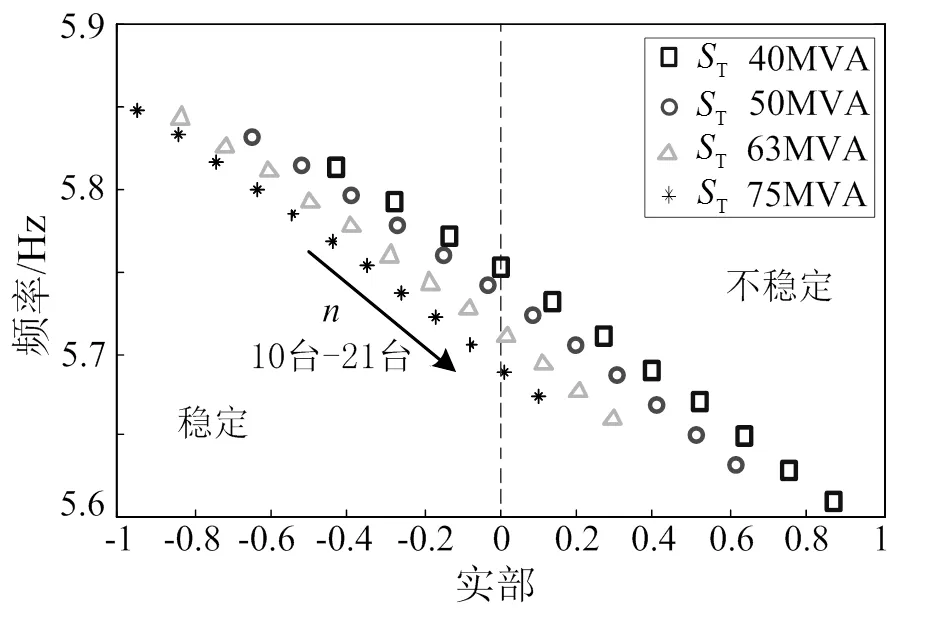
图15 主变压器容量对机车容纳量的影响

设D为相应主变压器容量下，牵引供电系统相对于31.5MV·A系统可容纳8台机车的基础上所增加的机车容纳量，它可以反映系统抑制低频振荡能力大小。DT为现有主变压器容量相对于31.5MV·A增大的容量。D/DT即为增大单位变压器容量使系统增加的机车容纳量，可反映增大主变压器容量时系统抑制低频振荡的效率。统计不同容量下系统抑制效率如表3所示。

表3 增大主变压器容量时系统抑制低频振荡效率统计

由表3可知，系统低频振荡抑制效率随主变压器容量的增大而降低，主变压器容量大于50MV·A后，增大容量，机车容纳量变化较小，考虑系统抑制效率优先选取变压器容量为40或50MV·A。理论上，在主变压器容量40MV·A，短路电压百分值8.4%条件下，系统可稳定运行的机车为12台左右；主变压器容量50MV·A，短路电压百分值8.4%下，系统可稳定运行的机车为15台左右，均可满足现场整备需要，更大容量的主变压器会造成成本过大，容量浪费，降低经济性。

4.5 方案优选

对比以上4种低频振荡抑制方案，供电侧治理方案可以从系统整体解决地区低频振荡问题，效果显著，且工作量集中，能有效提高车网系统机车容纳量，满足现场需要，优先选用。其他3种方案均有一定的局限性。

5 扩容方案抑制效果测试

将徐州枢纽变压器扩容方案提交中国铁路上海局综合审查后，最终确定采用主变压器容量为50MV·A，短路电压百分值为8.4%的扩容方案。2017年4月施工更换了新的主变压器，在扩容后3个月内徐州枢纽再未发生低频振荡问题。

为进一步测试改进后牵引供电系统对低频振荡的抑制能力，2017年7月20日中国铁路上海局在徐州枢纽组织了新一轮的低频振荡测试工作。测试共包含24种工况，具体测试内容见表4。测试方法为在机务段内同时升弓整备多台机车，利用设备观察多个地点电压电流波形，判断牵引供电系统是否发生低频振荡。机车上空调属于恒功率负载，根据文献[17]可知，在AC-DC整流系统中恒功率负载会削弱系统阻尼，降低系统稳定裕度，造成系统不稳定，当多台机车同时升弓整备瞬间会对牵引供电系统造成较大的电流冲击，如果系统稳定裕度不足，极易引发低频振荡。课题组重点测试了在较为极端的条件下，扩容变电所主变压器后牵引供电系统在多车同时整备的工况下对低频振荡的抑制能力。本文根据测试结果，选取其中5个典型工况按时间顺序逐一分析，典型波形均采用变电所输出馈线上电压电流波形。

表4 现场测试完整内容

5.1 测试工况1

机务段升弓整备8台HXD2B、1台HXD3C、4台HXD1D型机车，其中8台机车打开空调。如图16所示，升弓瞬间电流发生突变，但很快收敛稳定，电压保持稳定，系统未发生低频振荡。

图16 测试工况1变电所馈线上电压电流波形

5.2 测试工况2

机务段升弓整备8台HXD2B、1台HXD3C、4台HXD1D型机车，13台机车均打开空调。如图17所示，升弓后网侧电流小幅波动后趋于稳定，网侧电压未出现明显变化，系统在13台车同时整备的工况下仍未发生网压低频振荡。

图17 测试工况2变电所馈线上电压电流波形

5.3 测试工况3

机务段升弓整备11台机车，10台机车打开空调，1台HXD2B型机车带空调先降弓后升弓。如图18所示，升弓瞬间，网侧电流突增后很快趋于稳定，网侧电压较稳定，系统未出现低频振荡。

5.4 测试工况4

机务段升弓整备11台机车，9台机车打开空调，1台HXD2B和1台HXD3C带空调先降弓后升弓。如图19所示，机车全部升弓瞬间出现较大电流冲击，经过几秒后电流逐渐收敛于稳态值，网侧电压在升弓瞬间下降后逐渐恢复稳定。在大电流冲击下，系统仍未发生低频振荡。

图18 测试工况3变电所馈线上电压电流波形

图19 测试工况4变电所馈线上电压电流波形

5.5 测试工况5

机务段升弓整备11台机车，7台车打开空调，4台HXD1D型机车带空调先降弓后升弓。如图20所示，升弓瞬间网侧电流突变，随后趋于稳定。网侧电压在升弓瞬间下降后逐渐恢复到正常大小，系统未发生低频振荡。

图20 测试工况5变电所馈线上电压电流波形

5.6 测试结果

现场测试的24种工况中，系统均未出现低频振荡，与2016年1月测试结果相比，变压器扩容后整备区间机车容纳量上升到13台以上，与理论预测基本一致。不同型号、不同数量的机车带辅助系统同时升弓整备时，虽然会引起接触网上电流冲击，但由于车网系统稳定，网侧电流快速趋于稳定，不会引起低频振荡。

6 结语

本文针对徐州枢纽牵引供电系统的低频振荡问题，以HXD2B型机车为研究对象，通过建立车网系统传递函数模型，利用零极点判据分析了车网系统网压低频振荡的原因及各参数对低频振荡的影响规律，对比讨论了低频振荡的抑制措施。重点分析了徐州北变电所主变压器扩容技术方案，对比徐州枢纽在方案实施前后低频振荡测试的结果，表明该方案彻底解决了徐州枢纽低频振荡问题。该方案工作量集中，效果明显，弥补了仅调节机车参数的局限性，具有很好的适用性，值得推广应用。

[1] 中国铁道科学研究院. 大秦线HXD1型机车车网匹配关系测试报告[R]. 北京：中国铁道科学研究院，2008.

[2] 北京交通大学. CRH5动车组网压振荡牵引丢失测试分析报告[R]. 北京：北京交通大学，2010.

[3] 北京交通大学. HXD3B电力机车网压振荡牵引封锁测试分析报告[R]. 北京：北京交通大学，2011.

[4] 徐州北机务段. 接触网电压波动测试报告[R]. 北京：中国铁道科学研究院，2011.

[5] 西南交通大学. 徐州北枢纽供电电压异常波动测试报告[R]. 成都：西南交通大学，2016.

[6] WANG Hui, WU Mingli, SUN Juanjuan. Analysis of Low-Frequency Oscillation in Electric Railways Based on Small-Signal Modeling of Vehicle-Grid System in dq Frame[J]. IEEE Transactions on Power Electronics, 2015, 30（9）: 5318-5330.

[7] 周毅，胡海涛，杨孝伟，等. 电气化铁路车网耦合系统低频振荡分析[J]. 中国电机工程学报，2017，37（S1）：72-80.

[8] LIAO Yicheng, LIU Zhigang, ZHANG Guinan, et al. Vehicle-Grid System Modeling and Stability Analysis With Forbidden Region-Based Criterion[J]. IEEE Transactions on Power Electronics, 2017,32（5）: 3499-3512.

[9] 陶海东，胡海涛，姜晓锋，等. 牵引供电低频网压振荡影响规律研究[J]. 电网技术，2016，40（6）：1830-1838.

[10] 李群湛，贺建闽. 牵引供电系统分析[M]. 成都：西南交通大学出版社，2014：115-116.

[11] 宋文胜，冯晓云. 电力牵引交流传动控制与调制技术[M]. 北京：科学出版社，2014：30.

[12] CESPEDES M, SUN Jian. Impedance Modeling and Analysis of Grid-connected Voltage-source Converters[J]. IEEE Transactions on Power Electronics, 2014, 29（3）: 1254-1261.

[13] BAE B H, SUL S K. A Compensation Method for Time Delay of Full-digital Synchronous Frame Current Regulator of PWM AC Drives[J]. IEEE Transactions on Industry Applications, 2003,39（3）: 802-810.

[14] 董明，姜悦礼. HXD2型和HXD2B型电力机车电传动系统技术比较[J]. 机车电传动．2013（5）：45-48.

[15] 王晖. 电气化铁路车网电气低频振荡研究[D]. 北京交通大学，2015.

[16] 中华人民共和国铁道部. TB/T 3159-2007 电气化铁路牵引变压器技术条件[S]. 北京：中国铁道出版社，2007.

[17] YUNUS P N A M, JUSOH A, HAMZAH M K. AC-DC Single Phase Matrix Converter with a Constant Power Load (CPL)[C] // 2012 IEEE Symposium on Industrial Electronics and Applications(ISIEA), Indonesia：IEEE, 2012：275-280.

With regard to the low frequency oscillation in traction power supply system voltage of Xuzhou railway junction, the paper summarizes the regularities of current waveform of the low frequency oscillation network, establishes HXD2B locomotive related frequency domain impedance model and transmission function model of locomotive-network loop system, reveals the mechanism of low frequency oscillation and regularities influencing the low frequency oscillation by the system parameters; discusses the feasibility of schemes for suppression of 4 types of low frequency oscillation, finalizes the technical scheme for expansion of main transformers in traction substation, and puts forward in details the selection methods for capacities. The scheme is able to solve the problems of the low frequency oscillation effectively after testing, and it is worth for promotion and application.

Low frequency oscillation; frequency domain impedance model; traction transformer; scheme for suppression

10.19587/j.cnki.1007-936x.2018.06.004

U223.5+2

A

1007-936X(2018)06-0015-09

2018-04-03

杨 杰.西南交通大学电气工程学院，硕士研究生；

胡海涛.西南交通大学电气工程学院，副教授；

周 毅，陶海东.西南交通大学电气工程学院，博士研究生；

赵朝蓬.中国铁路上海局集团有限公司供电处，高级工程师；

何正友.西南交通大学电气工程学院，教授。

科技部国家重点研发计划项目（2017YFB1200802）；国家自然科学基金资助项目（51477145）。