谈“等效重力法”在2018年全国高考题中的应用及拓展
李春亚
(河北辛集中学,河北 辛集 052360)

图1
原题.(2018年全国理综Ⅰ卷第18题)如图1,abc是竖直面内的光滑固定轨道,ab水平,长度为2R,bc是半径为R的1/4的圆弧,与ab相切于b点.一质量为m的小球.始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动,重力加速度大小为g.小球从a点开始运动到其轨迹最高点,机械能的增量为
(A) 2mgR. (B) 4mgR.
(C) 5mgR. (D) 6mgR.
正确答案为(C).学生在分析这道题时,由于不清楚小球在圆弧上的速度变化情况,到底在圆弧上能否通过C点以及通过C点后的运动性质而导致出错.笔者在教学中使用“等效重力法”处理本题,起到了“拨云见日”的效果.
“等效重力法”,是在学习电场知识时引入的.该种方法通常是对处于匀强电场中的宏观物体,将重力与电场力合成为等效重力.以类自由落体运动、类竖直上抛运动、类斜抛和圆周运动为主要应用类型.它既是一种方法,也是高中阶段一种很重要的思想:等效思想.可以使学生在已有知识基础上,靠近其“最近发展区”,轻松突破新情境、新问题.而在实际教学中,学生却造成了这样的理解:只有在匀强电场中,才可以采用“等效重力法”.这样的理解就很片面.不仅在匀强电场中,物体受到除重力以外的其他性质的恒力时,采用该种等效方法,也可以起到“柳暗花明”的效果.
1 相关概念及运动特点
1.1 相关概念
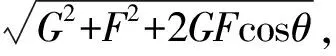

图2 确定等效重力
(3) 等效最低点.是指在等效竖直方向上,顺着F′方向的运动的最远点.如果在圆周运动中,也是指物体自由时能处于稳定平衡状态的位置.如图3中A点.注意等效最低点不一定是几何最低点.
(4) 等效最高点.是指在等效竖直方向上,逆着F′方向的运动的最远点.如果在圆周运动中,也是指物体与等效“最低点”关于圆心对称的位置.如图3中B点.同样注意等效最高点不一定是几何最高点.
(5) 类自由落体运动:初速度为0,加速度为等效重力加速度的匀加速直线运动.
(6) 类竖直上抛运动:初速度不为0,加速度为等效重力加速度,且初速度与等效重力加速度方向相反.
(7) 类斜抛运动:初速度不为0,加速度为等效重力加速度,且初速度与等效重力加速度方向不共线.
1.2 运动特点
(1) 圆周运动.
对称性:关于等效重力方向对称的点,如C、C′的速度、加速度大小相等.关于等效重力方向对称的两个运动过程的时间相等.
速度大小:在等效最低点,速度为最大值;在等效最高点,速度为最小值.
(2) 类自由落体运动:满足所有匀变速直线运动公式及推论.
(3) 类竖直上抛运动:上升下降过程中也具有速度以及时间的对称性.
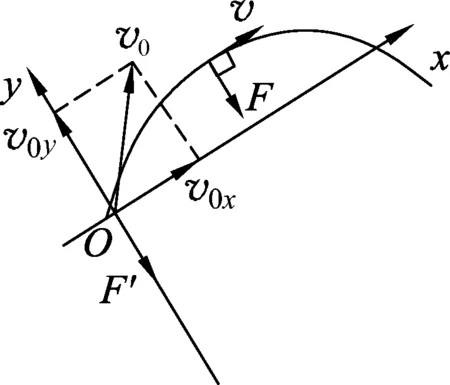
图4
(4) 类斜抛运动.
(如图4)沿垂直于等效重力方向建立x轴,等效重力方向建立y轴,将运动进行正交分解.

2 试题分析及拓展
2.1 试题分析

图5

2.2 试题拓展
拓展1(圆周运动).小球从a点开始到c点的过程中,何处小球的动能达到最大?动能最大为多少?
解析:(如图5)小球从a到b做匀加速直线运动,b到等效最低点d也加速,之后又减速到c点,所以d点位置处,小球的动能达到最大.(可以将图5顺时针转过45°便于观察等效重力做功)
b→d过程,利用动能定理
解得
拓展2(类斜抛).小球从c点飞出后,经历多长时间,速度为何方向时,到达类斜抛的速度最小点?并求出该速度最小值.

图6

3 总结
(1) 应用“等效重力法”的步骤.
观察物体受力特点,若除重力外,还受到其他恒力的作用,则可以考虑该方法→分析运动过程,类比相应运动(类自由落体运动、类竖直上抛运动、类斜抛运动、圆周运动等)→重力场中规律的迁移使用.
(2) 教学反思:“等效重力法”在处理除重力外,还受到其它恒力(不限于电场力)的作用的复杂问题时,可以类比重力场中运动,简化了过程,突出了主要因素,更有利于学生迅速抽象出物理情景,大大提高了解题效率,让学生科学的推理,在旧知识的基础上创新,将方法应用到新情境中,形成科学的思维能力.所以,在教学中应注意适时的使用.

