考虑微观渗流机理的致密气藏产量预测方法

陈中华 刘先山 寗 波 姜柏材 向祖平 秦正山 唐 欢 常小龙

1. 重庆科技学院石油与天然气工程学院, 重庆 401331;2. 中国石油集团科学技术研究院, 北京 100083

0 前言

致密气是我国非常规天然气勘探开发的重点资源之一[1],潜力巨大,累计探明地质储量3.3×1012m3,勘探开发前景好[2]。在开发过程中,产量预测是认识致密气藏开发规律、制定气藏开发规划决策十分重要而常用的方法之一。目前已有国内外学者对此进行了大量研究并提出了许多产量预测方法,经典的Arps J J、Fetkovich M J、Blasingame T A等人[3-5]的产量分析与预测方法由于未考虑启动压力和应力敏感等特殊渗流机理而不能用于致密气藏产量预测分析;在对启动压力、应力敏感有一定理论研究的基础上,Wu D、窦宏恩、刘志远、谷建伟、黄亮等人[6-10]通过实验进一步证实了致密气藏中启动压力梯度和应力敏感等微观机理对气井产量有较大影响,产量预测分析时不能被完全忽视;在此基础上,樊怀才、孙贺东、陈民锋、熊佩、严予晗、张强、伊向艺、方思冬等人[11-18]建立了仅考虑启动压力梯度或者仅考虑应力敏感的产量预测方法,可在某一影响因素起主导作用的情况下进行产量预测,但由于未同时考虑启动压力和应力敏感等特殊渗流机理,仍不能完全适用于致密气藏的产量预测。因此,本文在不稳定渗流理论的基础上,建立综合考虑启动压力和应力敏感的致密气藏直井产量预测模型,并提出一套图版拟合气藏关键参数的方法来确保产量预测模型中地质参数更符合实际情况,从而更加准确地预测致密气藏气井产量,为该类气藏的科学合理开发提供指导。

1 模型的建立

1.1 物理模型

顶底封闭的均质无限大致密气藏直井渗流物理模型见图1。

假设储层厚度为h,原始储层压力为pi,气井完全射开,以定标况下产量qsc生产,气水两相流体等温渗流,其中水相以束缚水形式存在,对气相渗流的影响考虑在启动压力梯度中,忽略重力与毛管力,考虑启动压力梯度与应力敏感效应的影响。

图1 致密气藏直井渗流物理模型

1.2 数学模型

由于致密气藏开采,使得储层孔隙压力降低,有效应力增加,导致其渗透率降低。参照Pedrosa定义的渗透率模量,针对气藏,用拟压力定义渗透率模量[19]:

(1)

式中:γ为渗透率模量(按拟压力定义),MPa-1;k为渗透率,10-3μm2;ψ为拟压力,MPa2/(mPa·s)。

积分得

k=kie-γ(ψi-ψ)

(2)

式中:ki为原始地层压力下的储层渗透率,10-3μm2;ψi为原始地层压力下的拟压力,MPa2/(mPa·s);e为自然常数。

其中气体拟压力函数定义为

(3)

式中:p为压力,MPa;p0为参考压力,MPa;μ为黏度,mPa·s;Z为偏差因子,小数。

状态方程为岩石状态方程和气体状态方程。

1.2.1 岩石状态方程

φ=φ0+Cf(p-p0)

(4)

式中:φ为储层压力p下岩石孔隙度;φ0为大气压力下岩石孔隙度;Cf为岩石压缩系数,MPa-1。

1.2.2 气体状态方程

pV=nZRT

(5)

式中:V为理想气体的体积,m3;n为气体物质的量,mol;R为理想气体常数;T为理想气体绝对温度,K。

当气藏存在束缚水时,气体分子在致密气藏中渗流时与其发生作用而被吸附,从而导致压力梯度高于一个值时,流体才流动,这一压力梯度阀值即为启动压力梯度[20]。考虑启动压力梯度的运动方程为

(6)

式中:v为气体流速,m/h;p为压力梯度,MPa/m;λ为启动压力梯度,MPa/m。

连续性方程为

(7)

式中:r为半径,m;ρ为天然气密度,kg/m3;t为时间,h。

无因次变量定义如下

(8)

式中:ψD为定产生产无因次拟压力。

(9)

式中:tD为无因次时间;Ct为综合压缩系数,MPa-1。

(10)

式中:rD为无因次半径;rw为井筒半径,m。

(11)

式中:γD为无因次渗透率模量;qsc为标况下的产量,m3/d。

(12)

式中:CD为无因次井筒储集系数;C为井筒储集系数,m3/MPa。

(13)

式中:λψ为拟启动压力梯度,MPa2/(mPa·s·m)。

(14)

式中:λψD为无因次拟启动压力梯度。

(15)

式中:ξD为无因次拟压力摄动解。

1.3 产量预测模型求解

将运动方程、状态方程带入连续性方程,并考虑启动压力梯度和应力敏感,根据无因次定义,结合初始条件、边界条件,建立考虑启动压力梯度及应力敏感的致密气藏无因次渗流数学模型如下:

(16)

式中:S为表皮系数。

利用摄动理论,取零阶摄动解进行化简并通过拉普拉斯变换于球坐标系,由内边界条件结合Lord Kelvin点源解所得的考虑启动压力梯度影响的致密气藏瞬时点源基本解,通过镜像反映法,对瞬时点源进行叠加,得顶底封闭边界瞬时点源的基本解,将该基本解沿直井井筒方向进行积分,得顶底封闭致密气藏直井井底压力响应函数拉氏解

(17)

式中:ξ0D为零阶无因次拟压力拉氏空间摄动解;K0( )为第二类零阶贝塞尔函数;α为积分变量。

其中RD、lD、zeD表达式为:

(18)

(19)

式中:L为任意参考长度,m;l为x,y,z三个参考方向。

(20)

式中:ze为z方向储层边界所在位置,m。

根据Duhamel叠加原理,可得考虑表皮效应和井筒储集效应的井底压力响应函数拉氏解:

(21)

式中:ξwD为考虑表皮效应和井筒储集效应的零阶无因次拟压力拉氏空间摄动解;u为拉氏变量。

通过Stehfest数值反演结果结合拟压力变换式,得到同时考虑启动压力梯度及应力敏感的致密气藏直井无因次拟压力解ψD,根据拉氏空间下定产压力解与定压产量解的关系[21]:

(22)

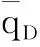
结合Stehfest数值反演及无因次产量定义,可得实空间致密气藏直井产量解。

2 产量拟合图版绘制与模型验证

针对致密气藏直井无因次产量预测模型,结合苏里格气藏某区块地层参数,使用MATLAB软件绘制考虑应力敏感及启动压力梯的无因次产量预测理论图版,见图2～3。把该区块两口井产量数据绘制到理论图版中,拟合出关键参数,来修正产量预测模型,并将其带入产量预测模型计算产量数据,然后将该区块两口气井生产资料分为两段,使用前半段与模型预测产量进行历史拟合,后半段与模型预测结果进行对比分析,以此验证模型的准确性。

图2 苏A井生产数据与理论图版拟合

图3 苏B井生产数据与理论图版拟合

苏里格气藏某区块基本储层参数:天然气相对密度为0.595 6,地面标准状态下压力为0.101 MPa,地面标准状态下温度为273.15 K,地层温度为317.15 K,地层厚度为22 m,原始地层压力为30.05 MPa,通用气体常数为0.008 314(MPa·m3)/(kmol·K),原始地层压力条件下渗透率为0.136×10-3μm2,井筒半径为0.062 m,孔隙度为0.080 5。将该区块某气井A与B的生产资料绘制到产量预测理论图版中。

图4 苏A、苏B井产量历史拟合及其预测曲线

3 敏感性因素分析

3.1 应力敏感对产量的影响

不考虑拟启动压力梯度,取不同无因次渗透率模量,绘制的无因次产量预测理论图版见图5。

图5 应力敏感影响下的无因次产量预测理论图版

由图5可知,应力敏感在前期已经对产量产生较大影响,说明应力敏感的存在,在前期使得储层渗透率受到伤害,无因次渗透率模量越大,应力敏感效应越强,储层受到的伤害越大,气体流动越困难,最终导致气井产量下降越快。

图6是图5图版中不同应力敏感下的无因次产量递减到5、4、3所需无因次时间的变化曲线。从图6可以看出,γD<0.000 1时,qD递减到5、4所需的无因次时间明显减少,表明应力敏感在前期已经使得产量递减加剧;γD>0.000 1时,气藏递减极快,由此可见,当图版拟合出的γD>0.000 1时,若不考虑应力敏感将导致产量预测误差较大。

图6 不同应力敏感下无因次产量递减到5、4、3所需的无因次时间

3.2 启动压力梯度对产量的影响

不考虑应力敏感,取不同无因次拟启动压力梯度,绘制的无因次产量预测理论图版见图7。

图7 拟启动压力梯度影响下的无因次产量预测理论图版

由图7可知,拟启动压力梯度对产量的影响主要在后期,拟启动压力梯度越大,气藏生命周期越短,后期递减幅度越大,其存在使得致密气藏物性更差,相同压差下气体突破启动压力梯度流动更加困难。

图8是图7图版中不同拟启动压力梯度下的无因次产量递减到5、4、3所需无因次时间的变化曲线。从图8可以看出,qD递减到5及λψD<0.001时qD递减到4所需的无因次时间几乎不受拟启动压力梯度的影响;qD递减到3及λψD>0.001时qD递减到4所需的无因次时间急剧减小。这表明开发初期,拟启动压力梯度对气藏产量递减几乎没有影响,开采进行到后期,特别是在λψD>0.001时,气藏产量递减将急剧增加。由此可见,当通过图版拟合出的λψD>0.001时,若不考虑启动压力将导致产量预测误差较大。

图8 不同拟启动压力梯度下无因次产量递减到 5、4、3所需的无因次时间

3.3 双因素共同作用对产量的影响

取不同无因次拟启动压力梯度、无因次渗透率模量,绘制的无因次产量预测理论图版见图9。由图9对比图5、图7可知拟启动压力梯度与应力敏感对产量的影响会产生叠加,使得产量递减曲线下掉幅度比两种因素单独作用时更大。

图9 拟启动压力梯度及应力敏感共同影响下的 无因次产量预测理论图版

4 结论

1)本文建立了考虑启动压力梯度和应力敏感的致密气藏直井产量预测模型,绘制了产量预测理论图版,提出了基于产量历史数据获取模型关键参数来修正产量预测模型、提高产量预测精度的图版拟合方法,并使用现场数据对比分析,其相对误差小,产量预测精度较高。

2)前期气井产量主要受应力敏感影响,应力敏感性越强则产量递减越快;当图版拟合出的无因次渗透率模量大于0.000 1时,气井产量快速递减,若不考虑应力敏感将导致产量预测误差较大。

3)后期气井产量主要受启动压力梯度影响,启动压力梯度越大则气井生命周期越短;当图版拟合出的无因次拟启动压力梯度大于0.001时,气井产量快速递减,若不考虑启动压力将导致产量预测误差较大。