金属筒形谐振陀螺的频率修调技术研究

于得川，齐国华，魏艳勇

(天津航海仪器研究所，天津 300131)

0 引言

金属筒形谐振陀螺属于固体波动陀螺的一种，该类陀螺用振动元件代替了传统机械转子陀螺的机械转子，用微幅振动取代了高速旋转，因而具有精度高、使用寿命长、稳定性好、能耗小、准备时间短、工作温度范围大、抗电离辐射能力强、对线性过载不敏感、机械部件结构简单等突出特点[1-3]。

金属筒形谐振陀螺的核心敏感部件为谐振子(图1(a))，其底部贴有压电陶瓷用于驱动和检测。该陀螺的工作原理为，压电电极的逆压电效应激励出谐振子的驱动模态(图1 (b))，陀螺敏感轴角速度的哥氏力效应激励出与驱动模态振形相差45°的检测模态(图1 (c))，压电电极的压电效应检测出谐振子的检测模态的振幅，最后压电电极的输出信号经外围电路解调，即可解算出敏感轴角速度[4]。

(a) 谐振子 (b) 驱动模态 (c) 检测模态 图1 金属筒形谐振陀螺核心部件及其工作模态Fig.1 The key components and work modes of metal cylindrical resonator gyroscope

理想情况下，由筒形谐振子的对称性可知，驱动模态与检测的固有频率是一致的，进而驱动模态与检测模态能够同时达到谐振，使陀螺具有最优性能。然而，由于加工误差、材料密度、应力分布不均、压电粘接不对称等非理想因素，导致谐振子在自由振动状态下出现2个相互间展成45°的固有轴系，谐振子沿着2个轴振动的固有频率分别达到极大值和极小值。这2个轴称为谐振子的刚性轴，极大值极小值的频率差称为谐振子的频率裂解。频率裂解将严重影响陀螺的零偏漂移、灵敏度等性能，过大的频率裂解甚至导致谐振子难以产生陀螺效应。因此，应进行必要的频率修调以减小或消除频率裂解[5-6]。

国外的洛杉矶加州大学[7-8]、斯坦福大学[9]、诺丁汉大学[10,14]以及国内的国防科技大学[1,11]、哈尔滨工业大学[12]、中国科学院电子学研究所[13]等机构，均已对相同原理的旋转对称结构的谐振子的频率修调理论及修调方式有了一定的研究。然而，目前对于该种陀螺的频率修调技术的研究尚缺乏系统化的修调理论的指导，使得修调过程难以量化。本文针对该金属筒形谐振陀螺的频率修调技术，阐述了一套更加系统、直观的修调理论，并进行了仿真和实验验证。由于固有频率与质量相关，通常谐振子的频率修调采用添加或者去除质量的方式。因此，本文就质量修调的方式进行理论、仿真和实验的研究。

1 频率裂解及修调理论模型

金属筒形谐振子的最主要振动部分为上端的谐振环，其频率裂解机理与环形谐振子一致，因此，筒形结构可套用环形谐振子的频率裂解模型。为了便于论文的表述和理解，这里引入2个概念：扰动模型和修调模型。扰动模型研究的是完美谐振子添加定量扰动能引起多少频率裂解的情况；修调模型研究的是带误差谐振子在何处添加多少扰动能修掉频率裂解。

1.1 质量扰动模型

现假设一理想无误差谐振环的质量为M0，谐振频率为ω0。如图2所示，在谐振环上添加N个质量点，每个质量点的质量为mi，周向位置为φi，i=1,…,N， 那么质量分布不均匀将导致相差45°的2个振型，低频和高频刚性轴周向位置为(ψ1,ψ2)，且

(1)

图2 添加质量扰动的谐振环Fig.2 Resonance ring with mass perturbation

这里不妨定义刚性轴位置为0～90°的波腹位置，根据诺丁汉大学的模型可知，低频刚性轴位置满足：

(2)

其中，α2为径向振幅与切向振幅的比值。并且频率极大值ω1与频率极小值ω2分别为：

(3)

其中，M为添加N个质量点之后的总质量。现定义频率裂解为极大值频率与极小值频率的差值，即频率裂解大于等于零。根据式(3)可得：

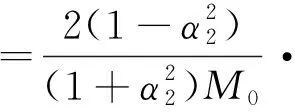
(4)

式(4)左边又可化为：

(5)

假设添加质量误差很小，则质量误差引起的频率裂解之后的谐振频率与原有谐振频率相差很小(对于一般机加工制造的谐振子，修形前的固有频率与修形后的固有频率相差小于0.5%)。因此，式(5)可进一步化为：

(6)

那么,将式(6)代入式(4)可得：

(7)

观察式(7)右边，暂且令：

(8)

将式(8)代入式(7)可得：

ω1-ω2=acos4ψ1+bsin4ψ1

(9)

由式(2)及式(8)可得：

(10)

综合式(8)、式(9)与式(10)可得：

(11)

为了进一步描述频率裂解及刚性轴角度位置，现引入2个参数σc、σs，称二者为裂解因子，表示带误差谐振子频率裂解的严重程度，二者的定义式如下：

σc=(ω1-ω2)cos4ψ1

σs=(ω1-ω2)sin4ψ1

(12)

即裂解因子可以通过测量频率裂解和刚性轴角度位置估算得到。根据式(11)和式(12)不难发现，频率裂解及刚性轴位置可用向量表示，(σc,σs)为用坐标表示的频率裂解向量，即：

(13)

(14)

(15)

式(15)即为频率裂解的质量扰动模型，显然质量点向量的和与其引起的频率裂解向量呈线性关系，即二者方向相反，模的大小为λ倍关系。

1.2 质量修调模型

现考虑一带误差谐振子，其初始频率裂解向量为Δ0ej4ψ01，对应的裂解因子为(σ0c,σ0s)。根据式(15)在谐振环上添加N个质量点进行频率修调，修调后的频率裂解可表达为：

(16)

修调后裂解因子所表示的向量为：

(17)

修调后的刚性轴位置满足的关系式简化为：

(18)

式(16)、式(17)、 式(18)即为带误差的谐振子的质量修调模型。质量修调的目的是寻找合适的质量点及其位置，使得修调后的频率裂解为零，或者裂解因子全为零，即：

(19)

将这一修调目的式代入式(16)或者式(17)，即可得到修调方程：

(20)

或者：

(21)

通过求解修调方程式(20)或者式(21)，即可求得质量修调的位置，以及需要添加或者去除质量的大小。然而，在上述修调方程中，质量敏感系数λ是一个未知量，需要在修调实验中进行标定。

对于以上修调模型，考虑一些特殊情况，可推导出一些简单的结论：

当N=1，即只添加一个大小为m1的质量点进行修调，设其位置为φ1，代入方程式(20)得：

Δ0ej4ψ01-λm1ej4φ1=0

(22)

求解以上方程可得2组解：

(23)

此组解代表添加质量点修调的情况：

(24)

此组解代表去除质量点修调的情况，其中，k=0,1,2,3。显然这里(4ψ01+2kπ)/4代表的是修调前的修谐振子的4个高频刚性轴的位置，(4ψ01+(2k+1)π)/4代表的是4个低频刚性轴的位置。

以上2组解表明，质量修调既可以在高频振型的4个波腹位置添加质量，也可在低频振型的4个波腹位置去除质量，如图3所示。两种修调方式对频率裂解的影响是一致的，但对2个极值频率的影响却有所不同：添加质量修调，会使高频振型的频率减小，使之朝着接近低频振型的频率变化，进而达到修调目的；去除质量修调的机理正好与之相反。

2 频率修调仿真

这里利用ANSYS有限元分析软件，通过模态分析功能，分别仿真了筒形谐振子的质量扰动模型和质量修调模型。

2.1 质量扰动模型仿真

如前所述，扰动模型研究的是完美谐振子添加定量扰动能够引起多少频率裂解的情况。首先在ANSYS中建立了完美无误差筒形谐振子的有限元模型，如图4所示。谐振子材料为XX合金，其材料属性如表1所示。

图4 筒形谐振子的理想有限元模型Fig.4 Ideal finite element model of cylindrical resonator

表1 金属谐振子的材料属性Tab.1 Material properties of metal resonator

通过模态分析可得谐振子的2个工作模态如图5所示，对应频率分别为x542.07Hz，x542.09Hz，频率裂解只有0.02Hz，可忽略不计，认为是理想谐振子。

图5 筒形谐振子的两工作模态Fig.5 Two working modes of cylindrical resonator

通过在谐振子唇沿上添加mass21单元模拟质量扰动，单元实常数的正负代表添加或者去除质量。分别在谐振子唇沿的任意角度位置，添加不同的质量点，进行模态分析，得到不同质量点对应的频率裂解如表2所示。

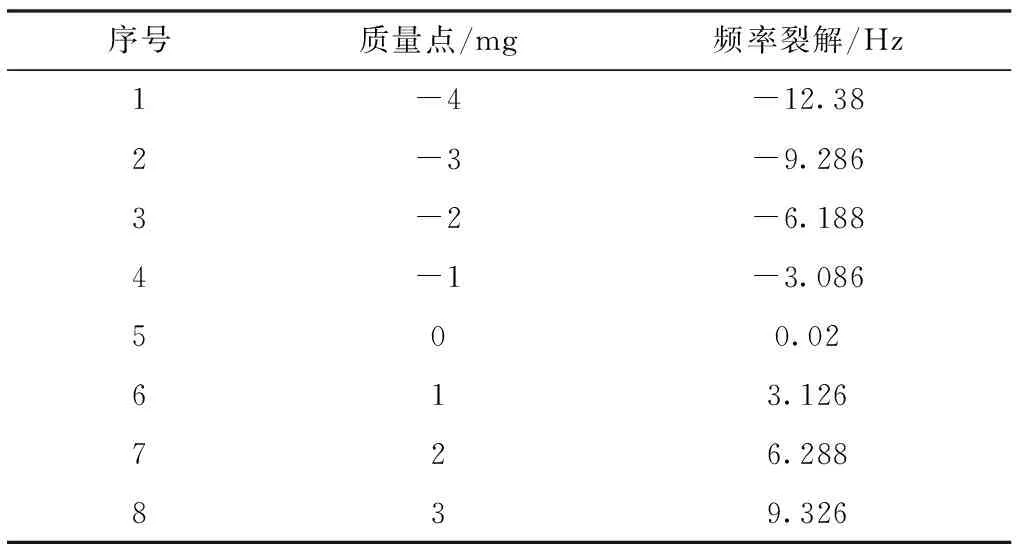
表2 不同质量点对应的频率裂解Tab.2 Frequency split corresponding to different mass points

同时，图6所示为频率裂解与质量点的关系曲线，不难发现，在固定位置添加质量点引起的频率裂解与质量成正比，符合扰动模型。比例系数即为式(15)扰动模型中的质量敏感系数λ，在图6中对应为直线的斜率。根据图6中直线的斜率，可以算得该结构的谐振子的质量敏感系数为 3.105mg/Hz。

图6 频率裂解与质量关系曲线Fig.6 Relationship curve of frequency split and mass

2.2 质量修调模型仿真

同样，修调模型考虑在带误差谐振子上添加质量点进行频率裂解消除的情况。在以上建立的无误差模型的基础上，通过该变谐振子局部单元的密度、杨氏模量使谐振子产生频率裂解。图7所示为一个带误差谐振子的频率裂解模型，其频率裂解大小为10.17Hz，高频刚性轴位置为76.83°，低频刚性轴位置为31.83°。

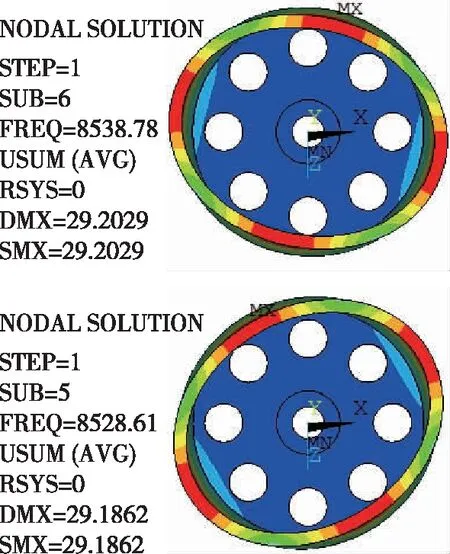
图7 带误差谐振子模态分析结果Fig.7 Modal analysis results with error harmonic oscillator

根据式(23)、式(24)可知，在谐振子唇沿76.83°、166.83°、256.83°、346.83°位置添加质量点，或者在31.83°、121.83°、211.83°、301.83°位置去除质量点(单元实常数为负)均可消除频率裂解。为保证谐振子的对称性，同时在4个对称的位置添加或者去除相同的质量。这里分别仿真了添加和去除不同质量频率裂解的变化情况，结果如图8所示。显然由式(22)可知，在刚性轴的正对位置添加或者去除质量，频率裂解与质量点大小呈线性关系，图8的仿真结果验证了这一结论。

(a) 高频轴加点修调

(b) 低频轴去点修调图8 添加正/负质量点频率裂解变化曲线Fig.8 Frequency splitting curve after adding positive/negative mass point

根据式(23)以及图8的仿真结果，最终在谐振子76.83°、166.83°、256.83°、346.83°位置添加3.274mg正质量点，频率裂解被修调至0.010Hz，在31.83°、121.83°、211.83°、301.83°位置，添加3.275mg负质量点，频率裂解被修调至0.011Hz。

3 频率修调实验

3.1 修调系统

根据恒弹性合金谐振子的特点，搭建了一套电磁激励、声场检测系统来测试谐振子的频率裂解及刚性轴位置。如图9所示，整套系统由谐振子及其支承座、微型转台、电磁铁、微麦克风、XY轴位移平台、频率响应分析仪、微型台钻组成。

采用NF FRA5097频率响应分析仪进行频率裂解的测试，测试原理如图9右边所示[15]。频率响应分析仪的OSC通道产生交流信号输出给INPUT1通道，同时给电磁铁进行扫频，电磁铁产生的交变磁力激励谐振子产生振动。对于在空气中振动的谐振子，其声压场的分布如图10所示，显然振形波腹处对应最高声压压强，在波节点处对应最低声压压强，并且声压变化的梯度方向指示了模态振型的方向，因此，采用微麦克风检测谐振子的振动信号。微麦克风将谐振子的振动转化为电压信号，输入到频率响应分析仪的INPUT2通道。通过一定频率范围的扫频，频率响应分析仪根据2个INPUT通道的幅值比实时地进行频率响应分析，从而能够得到频率响应曲线。幅频特性曲线的最大值点对应的频率即为谐振频率。

图9 频率修调系统以及模态测试系统原理图Fig.9 Principle diagram of frequency tunning system and modal test system

图10 谐振子振动时声压分布Fig.10 Sound pressure distribution in the vibration of a resonator

通过转动转台测试不同角度位置的频率响应曲线，即可判断出刚性轴位置及频率裂解大小。对于金属筒形谐振子，去除质量修调是最简单方便的修调方式，本实验采用微型台钻在低频轴对应角度位置轻微地钻出微槽实现质量的去除。

3.2 修调过程及结果

首先进行谐振子模态测试，当电磁铁对应谐振子上的激励位置没有对准某一刚性轴，而是处于两轴之间时，两模态位置均会受到电磁分力，扫频过程中两模态会被依次激励，扫频结果如图11(a)所示。通过转动转台调整激励位置，当频率响应曲线只有一个峰的时候，对应激励位置即对准了刚性轴的位置，图11(b)、(c)所示分别为对准低频轴和高频轴的情况，谐振子的频率裂解为8.72Hz，低频轴对应转台 11°、101°、191°、281°位置。

(a)

(b)

(c)图11 修调前谐振子扫频曲线Fig.11 Sweep frequency curve of resonator before tunning

根据仿真结果，该结构的谐振子对应的质量敏感系数为3.105mg/Hz，修掉该谐振子8.72Hz的频率裂解总共需去除2.8mg质量，平均分配到4个对称位置上，每个位置需要去除0.7mg质量。本实验所用微型钻台的钻头直径有0.6mm和0.4mm两种，0.6mm的钻一次去除量约为0.3mg，对应频率裂解约1Hz;0.4mm的钻用于精调，利用钻尖轻微钻一下可实现0.01～0.1mg的微量去除，对应频率裂解约0.03～0.3Hz。

图12所示为修调后的谐振子，谐振子唇沿上孔的编号对应打孔的顺序，每次修调后的频率变化情况如表3所示。

图12 谐振子打孔修调顺序Fig.12 Tuning sequence of resonator punch

表3 修调过程频率变化Tab.3 Frequency change of tunning process

表3的结果可按照上文已推导的算法进行修调，频率裂解得到有效减小，而且减小量近似于去除量，呈线性变化，再次验证了上述理论的正确性。根据打孔的体积与材料密度以及频率裂解的变化，估算该谐振子的实际质量敏感系数约为2.5mg/Hz,小于仿真结果(3.105mg/Hz),这是由于较深的孔降低了谐振对应位置的刚度。

4 结论

1)根据环形结构质量扰动模型，推导了修调质量点与频率裂解更加直观的向量形式，即频率裂解可表示为一向量，消除裂解向量的最佳方式即在其反向添加质量或者正向去除质量，构造负向量与其抵消。

2)针对金属筒形谐振结构，通过仿真与实验验证了这一理论，在高频刚性轴添加质量或者在低频刚性轴去除质量均可达到频率修调的目的，进而达到改善陀螺性能的目的。