相位检测误差对核磁共振陀螺输出频率的影响

江奇渊，罗 晖，杨开勇，赵洪常，汪之国，夏 涛，张 燚

(国防科技大学前沿交叉学科学院，长沙 410073)

0 引言

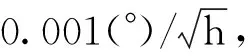
核磁共振陀螺通过测量原子系综核自旋的Larmor进动频率在惯性参考系下随载体转动的变化量来实现转动测量，而原子系综核自旋进动的测量通常是通过内嵌的磁力仪测量其磁化强度矢量来实现的。原子气室作为贮存其工作物质的容器，通常包含碱金属原子(Rb，Cs)、惰性气体原子(Xe，He)及缓冲气体[7-8]。碱金属原子不仅作为其内嵌的磁力仪的工作物质，同时通过光泵浦和自旋交换作用实现惰性气体原子核自旋的超极化[9]。由于核自旋产生的磁场很弱，单核自旋通常无法通过碱金属磁力仪实现探测，因此，需要对其原子系综进行探测。原子系综内各原子核自旋由于相位是随机的，因此，其横向宏观磁化强度矢量为零，无法探测到其Larmor进动频率，需要在横向施加一个与惰性气体原子Larmor进动频率相等的激励射频场来统一各原子核自旋的相位，实现其原子系综宏观的进动效应。最终通过记录这个实时跟踪惰性气体原子Larmor进动频率的激励射频场，实现转动测量。

因此，如何精确、实时地跟踪探测到的核自旋进动磁场，并施加反馈激励磁场，就成了核磁共振陀螺的关键技术之一。通常用于其信号跟踪的方法有反正切法、快速傅里叶变换法(Fast Fourier Transform，FFT)[10]、自激振荡以及锁相环方案[11]等，这些频率跟踪方案大多数都是通过探测信号的相位量进而得到频率值的。理想工作的频率跟踪方案能够实时跟踪探测信号的相位及幅度，并对时变的相位作微分处理得到信号的频率，但是由于相位延迟等因素导致的额外相位所引入的频率，无法与Larmor进动频率区分开，而这样的频率差值就可能会引入额外的测量误差。

核磁共振陀螺原子系综的输出频率测量精度决定了其作为陀螺仪的性能，因此，建立起它的频率误差方程，找出引起频率误差的因素，具有十分重要的意义。T.G.Walker等从理论上给出了核磁共振陀螺中惰性气体原子系综的输出频率的误差方程[12]，并从各个方面分析了各影响因素带来的频率误差量级。然而，此方程没有考虑频率跟踪方案可能引入的误差，目前也未见有将其考虑在内的频率误差方程。本文在假设频率跟踪方案理想工作的前提下，着重分析了通过测量相位跟踪核磁共振陀螺Larmor进动频率所引入的额外频率误差，并建立相应的误差方程。通过使用建立的误差方程进行仿真分析，得到各因素对额外频率误差的影响，最终找到抑制此频率误差的方案。

1 理论

考虑系统设置如图1所示，X轴施加激励射频场Bx=2B1cos(ω1t+β1)，其中B1为激励射频场有效幅值，ω1和β1为对应的圆频率和初始相位；Z轴磁场条件为Bz=B0+Bccos(ωct)，B0为Z轴静磁场强度，Bc为Z轴高频载波场强度，ωc为对应的圆频率。泵浦光极化方向沿Z轴正向，探测光沿X轴。PBS为偏振分光棱镜，PD为光电二极管，BPD为由2个PD组成的平衡探测器结构。原子气室内含有碱金属原子87Rb，惰性气体原子129Xe和131Xe以及缓冲气体。

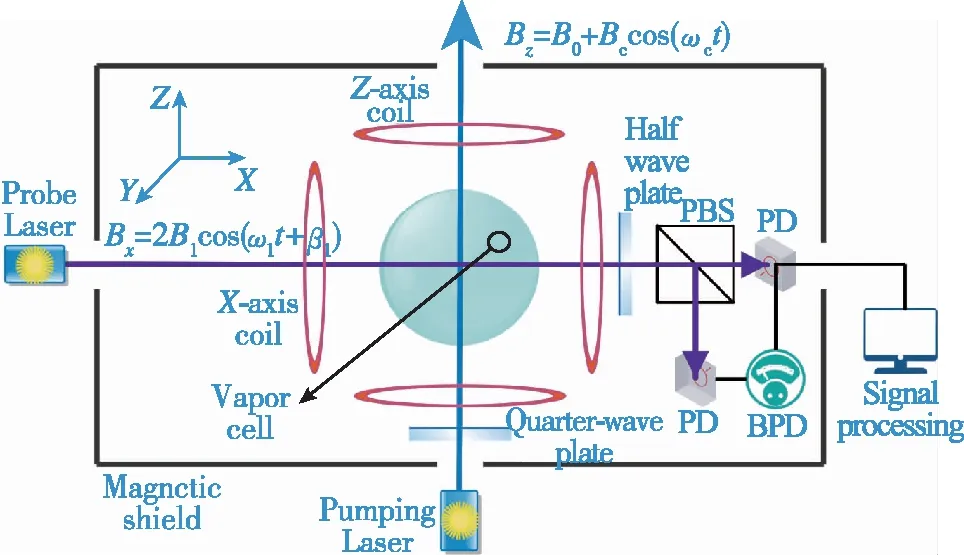
图1 核磁共振陀螺系统设置框图Fig.1 Systematic diagram of the nuclear magnetic resonance gyroscope

在这样的条件下，对原子系综进行基于Bloch方程的理论分析如下，系统的矢量Bloch方程为[13]：

(1)

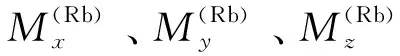
(2)

可得Rb的横向磁化强度如下[14]：

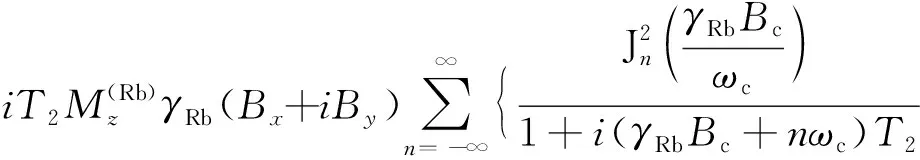
(3)

其中，Jn(·)表示n阶第一类Bessel函数，n为整数，p为正整数。根据共振条件γRbB0+nωc=0，设置载波场的频率,使其满足ωc≈γRbB0，可得观测的是n=-1条件下的磁化强度分量，则

(4)

(5)

使用锁相放大器对其进行基于一次谐波的解调低通，有

(6)

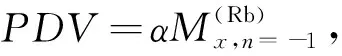
(7)

若进行更为细致的考虑，实际应用中通常只能设置ωc≈γRbB0，即γRbB0-ωc=0并不精确成立，而存在一个失谐量Δωz=γRbB0-ωc，则式(4)可变为

(8)

这里m表示修改的。同样式(5)也对应地修改为

(9)

得到基于一次谐波的解调低通信号

(10)

此时锁放解调低通后的X及Y输出通道的信号可表示为

FastXm=

(11)

FastYm=

(12)

考虑频率跟踪方案对探测到的信号(以X通道为例)进行估计跟踪，可假设其拟合输出的信号为：

FastXm=Acos(ωt+φ)+D

(13)

其中，A、ω、φ分别表示频率跟踪方案估计的幅度，圆频率和初始相位，D为估计的直流分量。为了方便表达，令

b1=ΔωzT2

c1=[J-2(γRbBc/ωc)-J0(γRbBc/ωc)]sinφ

d1=[J-2(γRbBc/ωc)+J0(γRbBc/ωc)]cosφ

则式(11)又可表示为

FastXm=a1[(c1+b1d1)Bx+(b1c1-d1)By]

(14)

根据所加的横向激励场和Xe本身在横向产生的磁场，可假设

Bx=2B1cos(ω1t+β1)+BXecos(ωXet+βXe)+Bx0

(15)

By=BXesin(ωXet+βXe)+By0

(16)

其中，BXe、ωXe和βXe分别表示Xe磁场的强度、圆频率和初始相位，Bx0和By0分别表示系统感受到的磁场在X、Y两轴上的分量直流部分。若假设频率跟踪方案能理想工作，则ω1=ω，β1=φ。根据式(13)～式(16)，有

Acos(ωt+φ)+D=a1{(c1+b1d1)[2B1cos(ω1t+

β1)+BXecos(ωXet+βXe)+Bx0]+

(b1c1-d1)[BXesin(ωXet+βXe)+By0]}

(17)

根据式(17)可得

D=a1[(c1+b1d1)Bx0+(b1c1-d1)By0]

(18)

[A-2a1(c1+b1d1)B1]cos(ωt+φ)=

a1BXe[(b1c1-d1)sin(ωXet+βXe)+

(c1+b1d1)cos(ωXet+βXe)]

(19)

sin(ωXet+βXe+βad)

(20)

其中，βad=arctan[(c1+b1d1)/(b1c1-d1)]，由式(20)可得

(21)

由于输出的圆频率值为所得相位在单位时间内的变化率，即ωoutput=d(ωt+φ)/dt，则有

(22)

可以看到，式(22)中等号右边第一项为Xe自旋的本征圆频率ωXe；第二项为Xe自旋初始相位的变化率ωβXe=dβXe/dt=0；第三项为锁相环跟踪频率所额外引入的相位差的变化率ωβad=dβad/dt。前两项的变化导致的频率测量误差在文献[12]中已有讨论，本文在不考虑前两项变化的基础上，着重考虑第三项，即锁相环探测陀螺频率所引入的误差。

由于通常使用信号发生器或是锁相放大器给线圈施加高频载波场并进行解调，而仪器所发生的信号的稳定性远高于系统内的其他参数。因此，可以假设Bc、ωc、φ为基本不随时间变化的常数，仅有Z轴的静磁场强度认为是时变量(横向驰豫时间T2此处也看作常数)。则c1、d1为常数，根据βad的定义容易求得

(23)

又

(24)

则式(23)可变为

(25)

考虑ωβad的变化引起的频率误差，对式(25)求微分，又由f=ω/(2π)，得到微扰带来的频率误差的表达式

(26)

通过式(26)即可预测B0不同的变化率及其二阶导数，以及失谐量的函数b1，对于锁相环引入频率误差的影响。

对于核磁共振陀螺来说，探测得到的Xe的Larmor进动圆频率ωXe=γXeB+ωr,与其所感受到的静磁场强度正相关，其中ωr为系统所感受到的转动圆频率。因此，在系统相对于惯性系静止的情况下，若需要使探测到的频率稳定，就需要使Xe感受到的静磁场稳定。然而在实际应用中，虽然地磁场等环境磁场的波动可以通过设置高屏蔽效率的磁屏蔽来进行被动抑制约6～7个数量级[15]，同时也可通过主动的磁补偿来进一步主动抑制约3～4个数量级[2]，磁场的影响仍然无法被忽略。为了抵消磁场带来的影响，通常使用Xe的2个同位素129Xe和131Xe来同时探测他们的Larmor进动圆频率[12,16]，如下所示：

ωXe129=γXe129B+ωr

(27)

ωXe131=γXe131B+ωr

(28)

其中，γXe129和γXe131分别为129Xe和131Xe的旋磁比。由式(27)～式(28)可以得到不受磁场影响的转动圆频率的表达式，即

(29)

通过双同位素方案可以从理论上消除磁场对转动频率的影响，但是式(29)并没有将相位引入的误差考虑在内，若将其考虑在内，则2个同位素的输出频率分别为

ωout129=γXe129B+ωr+ωβad

(30)

ωout131=γXe131B+ωr+ωβad

(31)

可以看到，此时2个同位素有一个相同的额外频率ωβad，若通过与式(29)相同的方式将磁场抵消，可得此时的转动圆频率的表达式

(32)

此时的转动频率就不可避免地受到式(26)的频率误差带来的影响，因此，在使用频率跟踪方案探测陀螺频率时，如何抑制这个误差就显得尤为重要。

2 仿真设置

考虑与实验情况接近的参数设置，对频率跟踪方案探测陀螺频率所引入的误差进行具体的数值仿真分析,其中Rb的横向驰豫时间采用文献中的经典值[14]，实际实验中可能会有不同的数值，但并不影响本文的分析。具体的基本参数设置如表1所示，其余的参数设置根据具体的仿真分析而定。

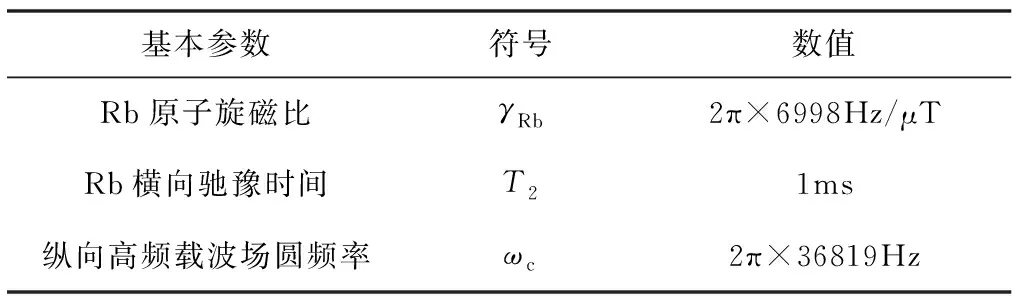
表1 参数设置Tab.1 Parameter settings

3 仿真分析

根据式(26)考虑不同的b1、dB0/dt、δB0和δ(dB0/dt)对δfβad的绝对值的影响，仿真结果如图2～图6所示，注意仿真结果图的坐标轴均采用双对数轴表示。这里磁场变化率及变化量的取值考虑目前电路水平一般能够达到的范围，并适当加大来考虑各因素的影响。

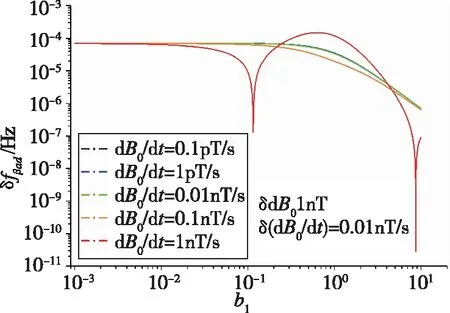
图2 频率误差在不同dB0/dt条件下随b1的变化曲线Fig.2 Curve of frequency error vs.b1 with different dB0/dt

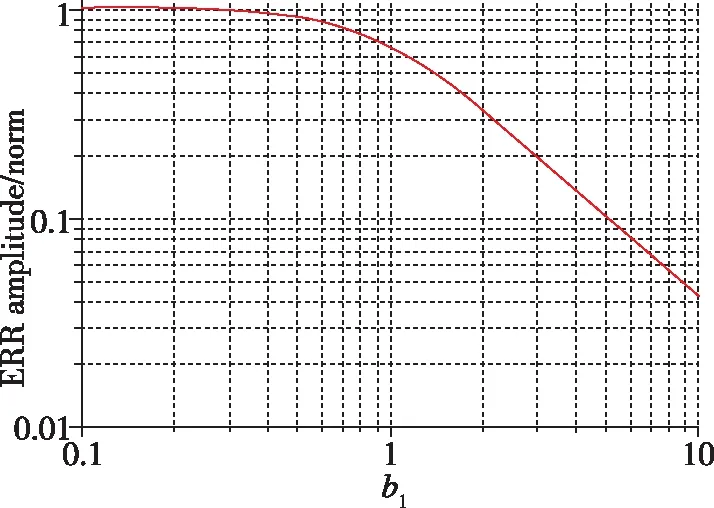
图3 EPR归一化强度随b1的变化曲线Fig.3 Curve of normalized EPR amplitude vs.b1

图2和图3在给定微扰值δB0=1nT和δ(dB0/dt)=0.01nT/s的情况下，考虑不同的b1和dB0/dt条件下|δfβad|的变化规律。其中图2为|δfβad|随b1的变化曲线，图中各不同颜色的曲线分别表示磁场变化率dB0/dt=10-4,10-3,10-2,10-1,1(nT/s)。可以看到，在磁场变化率较小时(dB0/dt≤10-1nT/s)，|δfβad|随b1的增加而呈现下降趋势；而当磁场变化率较大时(dB0/dt>10-1nT/s)，|δfβad|随b1的增加则总体呈现先增大后减小的趋势。值得注意的是，当dB0/dt>10-1nT/s时，曲线在b1的不同取值处出现了局部的极小值，最小值甚至达到了10-10Hz量级。虽然这样的结果确实给出了大幅抑制甚至消除额外频率误差δfβad的可能性，但是从式(26)中不难发现，这样的极小值的出现是由于二阶微扰项δ(dB0/dt)的存在，而实际上要精确控制磁场的二阶微扰项是极其困难的。因此，通过这样的极值点来抑制或消除δfβad并不可靠。另一方面，注意到当b1≥1时，所有曲线均呈下降趋势，因此，通过选取一个相对较大的b1值，可以至少把δfβad抑制1个数量级。但是b1值并不是越大越好，因为它越大，就表示与n=-1的共振点越偏离，从式(11)可知，过大的b1值会造成信号衰减过大。因此，需要根据信号强度和频率误差选择一个合适的值。由式(11)对电子顺磁共振(Electron Paramagnetic Resonance,EPR)强度随b1值的变化进行了仿真，仿真结果如图3所示，其中对强度进行了归一化处理。

从图3中可以看出，随着b1的增大，EPR归一化强度开始基本不变，直到b1≈1时，则开始迅速下降。若将EPR归一化强度下降1个量级作为信号探测的边界条件，即超过1个量级即无法探测，则要求b1≤5。另一方面，从图2中可以看出，当b1≈5时，|δfβad|相对于b1≈0时约有1个数量级的降低；b1≈10时更是有约2个数量级的降低；考虑到信号强度衰减b1取值在1～5之间较为合适，b1=5则能在实现信号探测的前提下最大程度地降低频率误差，其通过设置合适的ωc或B0则很容易实现，同时相对于b1≈0时的抗干扰能力也强很多。在此基础上，通过降低磁场的扰动可以进一步降低频率误差δfβad。

图4所示为|δfβad|随dB0/dt的变化曲线，各不同颜色的曲线分别表示为b1=10-3,10-2,10-1,1,10。除去与图2类似的局部极小值之外，不同于图2的是，|δfβad|随dB0/dt的增长基本呈现平稳的趋势，仅在磁场变化率较大时(dB0/dt≥0.01nT/s)才开始变化，其下降的趋势是由于局部最小值的存在，不考虑局部最小值则其基本保持不变或呈现上升趋势(b1=1)。因此，只要将磁场变化率控制在较小的量级，其对额外频率误差的影响基本是不变的。对比图4中不同的曲线可以清楚地看到，b1=10比b1=10-3时|δfβad|降低了约2个数量级，这与图2的结果也完全符合。

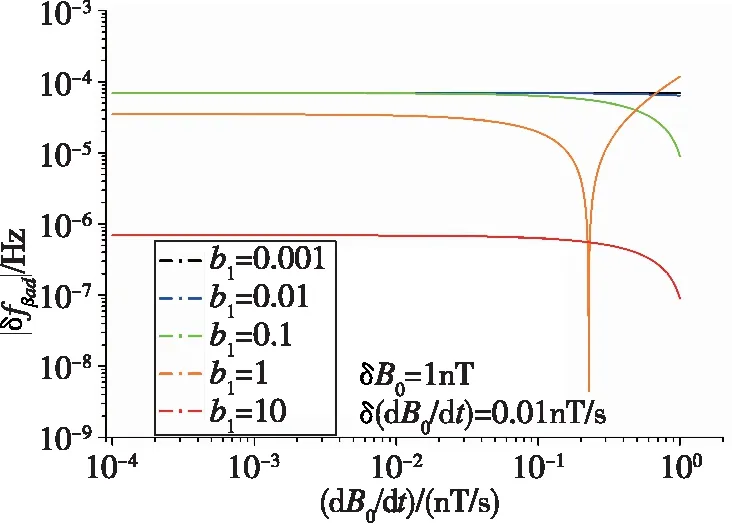
图4 频率误差在不同b1条件下随dB0/dt的变化曲线Fig.4 Curve of frequency error vs.dB0/dt with different b1

图5和图6则在给定条件b1=5和dB0/dt=0.01nT/s的情况下，考虑不同的微扰值δB0和δ(dB0/dt)对 |δfβad|的影响。其中图5为|δfβad|随δB0的变化曲线，图中各不同颜色的曲线分别表示静磁场二阶微扰量δ(dB0/dt)=10-6,10-5,10-4,10-3,10-2(nT/s)。与图4类似，除去局部极小值外，在二阶微扰量较小时(δ(dB0/dt)≤0.01pT/s)，|δfβad|随δB0的增加而基本不变；在二阶微扰量较大时(δ(dB0/dt)>0.01pT/s)，则呈现先平稳后单调递增的趋势。目前的电路水平一般至少能够将电流导致的磁场变化抑制在0.01nT/s左右，而变化率的微扰量则更低，至少可以达到1pT/s的水平。注意到随着磁场的二阶微扰量δ(dB0/dt)降低1个数量级，|δfβad|也对应降低1个数量级，这从式(26)中也容易得到。因此，通过降低磁场的二阶扰动，可以进一步地有效降低额外频率误差δfβad。

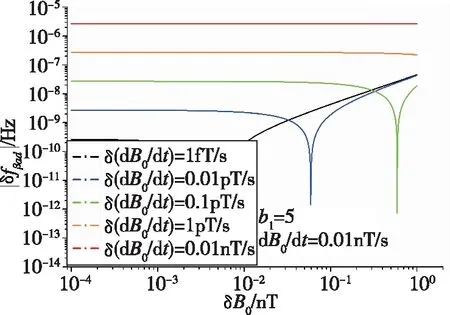
图5 频率误差在不同δ(dB0/dt)条件下随δB0的变化曲线Fig.5 Curve of frequency error vs.δB0 with different δ(dB0/dt)

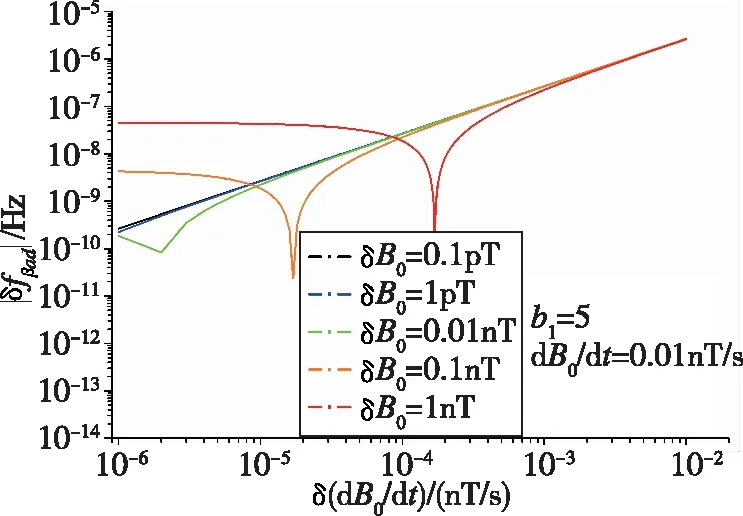
图6 频率误差在不同δB0条件下随δ(dB0/dt)的变化曲线Fig.6 Curve of frequency error vs.δ(dB0/dt) with different δB0

图6所示为|δfβad|随δ(dB0/dt)的变化曲线，各不同颜色的曲线分别表示静磁场微扰量δB0=10-4,10-3,10-2,10-1,1(nT)。同样不考虑局部极小值的情况下，|δfβad|随δB0的增加而呈现先平稳后单调递增的趋势，这是由于式(26)中δfβad与磁场的一阶微扰量δB0和二阶微扰量δ(dB0/dt)均呈线性关系。因此，可以看到，在较小的静磁场二阶微扰量的条件下，通过抑制磁场的一阶扰动，同样能起到降低额外频率误差δfβad的作用。

通过图2～图6的分析，可以做一个简单的计算，首先在b1=5和dB0/dt=0.01nT/s的条件下，假设一个通过简单控制就易于达到的磁场扰动值δB0=1nT及静磁场二阶微扰量δ(dB0/dt)=1pT/s，可得|δfβad|=0.224μHz，对于高精度陀螺(导航级)，这样的误差是无法忽略的；而在同样的条件下，如果通过抑制磁场扰动值使其达到δB0=1pT以及相同的静磁场二阶微扰量δ(dB0/dt)=1fT/s，可以得到|δfβad|=0.224nHz，这样的频率误差换算成转速为2.9×10-4(°)/h，已经远小于导航级的转速误差量级，可以认为对于导航级的陀螺其误差可以忽略。

4 结论

1)本文基于Bloch方程推导了核磁共振陀螺输出频率的表达式，考虑了频率跟踪方案的探测相位引入的额外频率误差，并通过频率误差方程着重对引入的额外频率误差进行了仿真分析。

2)仿真结果表明，频率跟踪方案的探测相位引入的额外频率误差主要受到Z轴静磁场强度及其一阶变化率的影响。一方面通过选择合适的Z轴静磁场强度或载波场频率使得其产生一定的失谐量，可以至少将引入的额外频率误差抑制1个数量级；另一方面，通过减小Z轴静磁场的一阶及二阶扰动，其也会得到对应的抑制，结合两者可以将额外频率误差抑制4个数量级至亚nHz量级，在导航级陀螺精度时已可以忽略。

3)本文首次将频率跟踪方案的影响考虑在核磁共振陀螺的频率误差方程内，目前并未见有考虑了测频方案影响的频率误差方程的报道。

4)本文并未考虑碱金属原子的横向驰豫时间随时间变化的情况，而这一项的变化也会对额外频率误差产生贡献，下一步将对其进行深入分析。