汉江上游径流非一致性演变特征及频率分析

滕 杰， 郭 明， 周政辉

(1.济南市卧虎山水库管理处， 山东 济南 250115； 2.中国水利水电科学研究院， 北京 100038；3.辽宁师范大学 城市与环境学院， 辽宁 大连 116029； 4.河南省漯河水文水资源勘测局， 河南 漯河 462000)

1 研究背景

水文频率分析是设计洪水计算及确定重现期的有效途径，是水利工程设计实施的重要理论保证[1]。目前水文频率分析方法的基本假设前提是水文要素序列满足一致性要求，即水文极值的概率分布情况或统计规律在过去、现状和未来均不发生变化[2]。然而，受到全球和区域气候变化和高强度人类活动的双重影响，流域气候特征和降雨径流关系均发生了显著变化[3]，导致水文序列统计一致性不再成立，即非一致性变异[4]，在非一致性条件下的水文频率分析成为水利工程规划、设计与运行中需要解决的迫切问题，也是水文科学研究中的热点问题。近年来，国内外研究学者对水文非一致性分析开展了大量研究[5-9]，梁忠民等[2]总结了国内外非一致性水文频率分析的代表性研究成果，系统分析了不同方法的适用性。熊立华等[10]对国内外洪水分析方法进行了评述，并指出洪水频率分析系列需遵循一致性的原则。目前对水文频率分析方法主要分两大类：(1)将变异水文序列拆分为表现非一致性的确定成分及一致性的随机成分。对于该类方法我国学者谢平等[11]研究较深入，通过分离非一致性水文序列中的随机性及确定性(趋势、跳跃等)成分，对随机性成分直接进行频率分析，对确定性成分进行拟合，再将两部分结果进行合成，进而得到非一致性水文序列的频率分布。基于该方法的实例研究成果颇丰，如叶长青等[12]对存在趋势变异的东江流域洪水序列进行分析，并探讨了重现期的变化；冯平等[13]对水文序列非一致性参数估计的不确定性影响进行了研究，得到经一致性修正后的序列对洪水预报可靠性将得到提高的结论。(2)建立分布函数参数与解释变量之间的函数关系。国外研究学者多以第二类方法构建非一致性洪水频率分析模型，进行频率分析。Rigby[14]等提出广义可加模型，通过该模型构建分布函数参数和多个解释变量的线性、非线性、参数和非参数关系，并增大了分布函数的选择范围(包含高峰、高偏分布及指数族、非指数族分布)，灵活性较高，但该种方法对模型精度要求较高，较第一类方法实用性较低。

本文以汉江上游3个具有代表性的水文测站为例，基于长序列日径流量资料，应用趋势分析及非一致性检验方法，分析汉江上游径流量变化趋势及确定变异前后对应不同气候及下垫面条件不同保证率下水文设计值的变化情况，以期为汉江流域防洪减灾、水利工程合理调控，以及引汉济渭和南水北调等调水工程的调度运行提供技术支撑。

2 研究区概况与数据来源

2.1 研究区概况

汉江是长江最大的支流，全段长1 577 km、流域面积15.90×104m2，北部干流与秦岭山脉平行，海拔大于2 500 m；南部界线为米仓山与大巴山，平均海拔2 000 m左右[15]。汉江干流丹江口以上为上游，河长925 km，占干流总长度的59%，控制流域面积9.52×104km2，流域内多年平均降水量917.7 mm，径流量388×108m3。

汉江流域上游已建有大中小型水库共计937座，其中包含总库容达222.64×108m3的大型水库4座。此外，还有引水工程共计13 335处，设计供水能力为14.78×108m3，提水工程9 921处，设计供水能力为3.44×108m3。同时，汉江上游还有引汉济渭等大型跨流域调水工程，丹江口水库也是南水北调中线工程的起点，因此，汉江上游的水资源和防洪安全对汉江流域、关中平原和南水北调中线受水区有着显著影响。

2.2 数据来源与处理

本文选取汉江干流上游的武侯镇、洋县、安康3个典型水文测站为分析对象(图1)，应用3站1967-2014年长序列逐日径流数据，并对个别缺测数据根据临近年份的降水径流关系进行插补，各站点具体信息如表1所示。

图1 区域概况及选站分布情况

序号站点测站编码集水面积/km2多年平均降水量/mm多年平均径流量/108 m31武侯镇618000003092803.0102洋 县6180060014484827.3543安 康6180130038625843.0181

3 研究方法

3.1 线性趋势与突变检验

根据逐年径流量的趋势变化特点，用x=a+bt进行线性拟合。其中，a、b由最小二乘法确定，b为年径流量的倾向率，倾向率的大小表明年径流量的变化幅度[16]。同时b值可判断径流趋势的变化情况，b>0，说明序列趋势为增加，b<0，说明序列趋势递减。

为提高检测出非一致性突变点及突变时期的精度，本文将Mann-Kendall及Lee-Heghinan突变检验法相结合，对序列进行突变点检验。Mann-Kendall突变检验法是非参数检验法的一种，由于其不需要样本服从一定的分布，受异常值干扰较小且计算较简便等特点，被广泛应用于气候及水文序列的趋势性分析。其公式如下[17]：

(1)

式中：E(sk)、Var(sk)分别为累计数sk的均值及方差，其计算公式为[17]：

(2)

Lee-Heghinan检验法是假定序列总体满足正态分布及分割点τ的先验分布均匀，推求其后验条件概率的密度函数，进而由后验概率密度函数反推满足条件的分割点的方法。该方法能较好地检验出均值发生变异的序列，是检验跳跃变异的有效方法。其公式如下[18]：

(3)

(1≤τ≤n-1)

由于Mann-Kendall突变检验法计算简便，且对数值精度要求较低，因此检验出的突变可能存在虚假突变的情况；而Lee-Heghinan检验法检验所得的跳跃突变点是唯一的，综合两种检验方法可有效提高检验结果的可信度，便于为后续的水文频率分析提供更加可靠的数据基础。

3.2 非一致性条件下水文频率分析

水文频率分析的假设前提是序列满足一致性要求，谢平等[19]提出实测水文变异序列由理想的平稳性即一致性成分与随机性成分线性组成，通过对变异分割点前后的一致性修正，获得修正后总体的统计特征参数。

假设变异点为τ，序列被分割为x1,x2,…,xτ和xpxτ+1,…,xτ+n两部分，变异前后序列均值分别为Exa与Exb，变异的水文序列可表示为[20]：

Ex=α·Exa+(1-α)·Exb

(4)

式中：α为突变点前的权重，由Exa与Exb确定，公式如下[20]：

(5)

由于Ex可以通过公式(4)、(5)联合求出，其中f(t)为确定性趋势成分，因此，随机性成分可以表示为[20]：

y(t)=f(t)-Ex

(6)

则经过一致性修正后的序列可以表示为[20]：

Y(t)=x(t)-y(t)

(7)

采用Pearson-Ⅲ型概率密度函数[21]对水文序列进行频率分析，从而确定径流序列不同保证率下的水文设计值。

4 结果分析

4.1 年径流演变分析

根据武侯镇、洋县、安康3个水文站点的逐日径流量数据，计算各测站年平均径流量，绘制1967-2014年年均径流序列变化趋势(图2)。从图2可以看出，3站年平均径流量均呈递减趋势，其中，递减速率安康站(-25 m3/10a)>洋县站(-11 m3/10a)>武侯镇站(-0.16 m3/10a)，但3站的递减趋势均未通过显著性检验，递减趋势不显著。

武侯镇地处汉江上游，所处源头地区水利工程设施较少，下垫面条件受人为影响不大，加之武侯镇年均降水量小于其他两站，基础水量及天然补给水量少，因此径流量递减率最小。洋县位于汉江上游中部地带，测站附近有少数水利工程设施，人为取用水量相应增加，下垫面条件受人类开发活动影响，因此洋县站径流量的递减趋势大于武侯镇。安康与汉江中上游分界处距离较近，是汉江上游干流与多支流交汇地带，汇水量较上游大得多，且测站附近水库、大坝及水电站等水利枢纽工程较多，人为取用水对径流影响增大，从而导致径流量减小趋势较大。武侯镇、洋县及安康3个水文站的径流量年最大值出现年份分别为1981、1981及1983年，安康出现最大径流量的年份略晚于洋县及武侯镇，说明下游径流量的变化受上游影响较大，且略滞后于上游。

对1967-2014年年平均径流量序列进行M-K非一致性检验，结果见图3。从图3可以看出，武侯镇发生突变年份可能为1975年、1982-1984年期间及2009年；洋县1967-1979年间可能存在多个突变点，1990年及2009年也可能有突变现象发生；安康1969-1973年间、1987年及2011年可能存在突变现象。

图2 1967-2014年年平均径流量序列趋势变化图

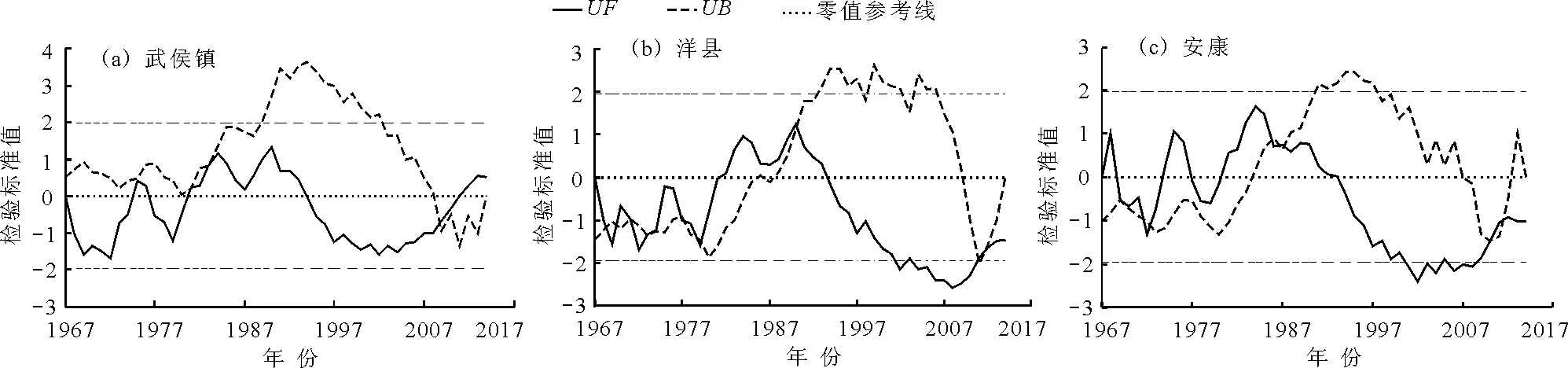
图3 1967-2014年年平均径流量M-K检验图

武侯镇、洋县与安康3站间可分为武侯镇-洋县及洋县-安康两段区间汇水过程，根据各测站及区间汇水的年平均径流量，统计得各测站与区间汇水径流量情况如表2。由表2可以看出，下游测站的径流量为上游测站与区间汇水的径流量之和。其中，武侯镇-洋县区间汇水水量占洋县测站水量的81.48%，洋县-安康区间汇水水量占安康测站水量的70.17%，说明区间汇水是导致测站径流量增大的主要原因，控制性较强。

表2 测站及区间汇水径流量

根据区间汇水年径流序列绘制趋势变化图(图4)，两段区间汇水径流量均呈递减趋势，武侯镇-洋县段的递减率大于武侯镇小于洋县，洋县-安康段的递减率大于洋县小于安康，说明区间汇水的径流量减少对于洋县及安康的径流量减少大于上游测站的贡献率。

根据区间汇水的M-K非一致性检验结果(图5)，武侯镇-洋县段汇水突变年份为1991年，洋县-安康于1969-1973年间、1986年及2010年存在突变。洋县及安康两站的检验结果与区间汇水检验的突变时间相近，但略有滞后，说明区间汇水径流量的变化对下游测站的径流量变化影响较大，与上述所得区间汇水对下游测站水量变化控制性较强的结论一致。

4.2 年最大日径流演变分析

根据3站多年年最大日径流数据，绘制年最大日径流变化趋势图(图6)，武侯镇站年最大日径流量呈微弱增加趋势，洋县及安康站逐渐递减。本文基于年最大日径流数据，检测非一致性确定变异时期，为进一步的水文非一致性频率计算提供数据基础。

非一致性检验的方法很多，但不同方法检验出的变异结果存在差异。为提高检验结果的准确性，采用近年来应用广泛的Mann-Kendall及Lee-Heghinan检验法对3站年最大日径流序列变异时期进行综合检验分析，以保证所得结果具有较高的可信度，为进一步分析水文频率提供较可靠的数据。

首先对3站年最大日径流序列进行Mann-Kendall检验，检验结果如图7所示。由图7武侯镇站的检验结果，UF与UB曲线在0.05显著性水平线间有交点，存在突变现象，突变年份为1991年；根据洋县站的检验结果，UF与UB曲线在0.05显著性水平线间存在多个交点，可能出现突变的时间为1970年、1986-1992年间及2012年；由安康站的检验结果，1987年可能存在突变现象。由于Mann-Kendall突变检验法检测出的突变年份较多，可能存在虚假突变情况，因此，进一步采用Lee-Heghinan检验法检测变异年份。

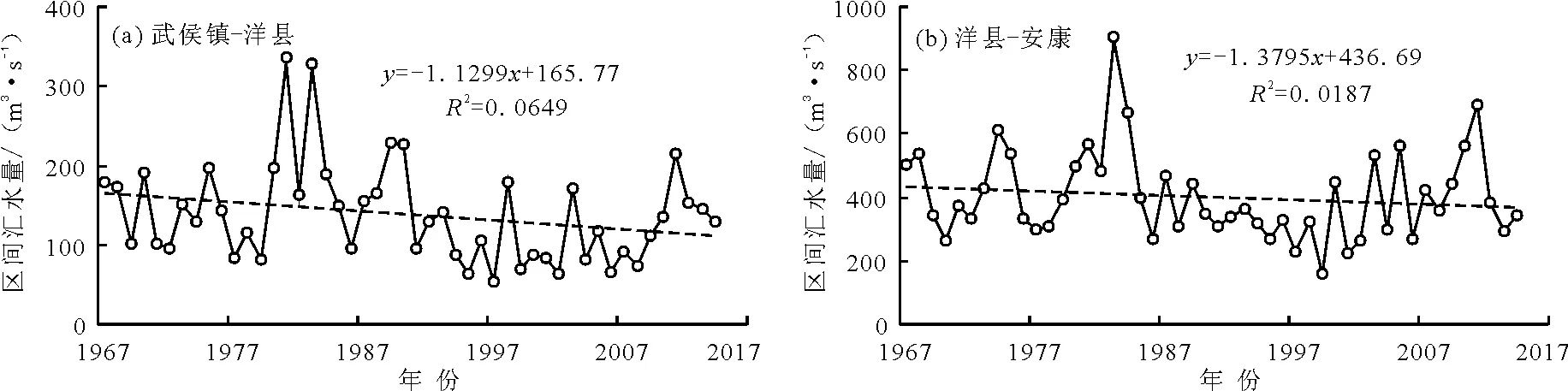
图4 1967-2014年3站点区间汇水年径流序列

图5 1967-2014年3站点区间汇水M-K检验

图6 1967-2014年年最大日径流序列

图7 1967-2014年3站点年最大日径流序列M-K检验

根据Lee-Heghinan检验法对各站的径流系列的变异进行检验，所得结果如图8示。Lee-Heghinan检验法是根据分割点(即：跳跃突变点)前后的概率密度函数值的大小判断突变点的方法，概率密度函数值越大的点是突变点的可能性越大。武侯镇与洋县的检验结果均为1991年，安康为1997年。综合两种突变检验结果，发现武侯镇与洋县的拟合程度较高，可确定1991年为突变年份。安康两种方法所得结果有10 a的偏差期，拟合程度较低。

4.3 水文频率非一致性分析

为进一步明确水文序列变异前后对水文频率的影响，对3站年最大日径流序列进行非一致性修正分析。基于非一致性检验结果，武侯镇与洋县突变年份均为1991年，安康两种检验方法所得突变年份分别为1987与1997年，考虑下游径流序列的突变存在滞后性，因此以1992年作为安康的突变年份，突变将3站的径流序列分割为1967-1990年与1991-2014年及1967-1991年与1992-2014年两个时间段。本文以1967年作为历史修正参照年，2014年作为近期修正参照年，首先对3站的年最大日径流序列进行一致性修正，剔除较稳定的趋势项，对修正后的序列进行趋势检验，绘制趋势变化图(图9)。从图9中可以看出，历史及近期修正后的序列不存在或存在可忽略不计的趋势成分，趋势性成分对序列影响较小，基本满足一致性条件的假设，可进一步采用Pearson-Ⅲ法计算基于历史及近期修正后年最大日径流序列不同保障率下水文设计值，并确定设计参数。首先对各站基于不同时间修正后及未修正的径流序列进行经验排频，按降序排列，然后采用Pearson-Ⅲ型水文频率计算软件对排频后的径流序列进行计算，其各自模型参数及结果见表3，基于历史及近期修正前后年最大日径流量频率曲线见图10。

图8 1967-2014年3站点径流序列Lee-Heghinan检验

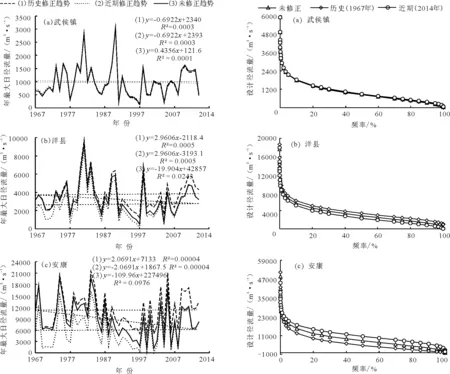
图9 1967-2014年3站点年最大日径流量趋势检验图10历史及近期修正前后年最大日径流频率曲线

表3 最大日径流历史及近期修正前后不同频率设计值

注：历史修正及近期修正分别基于1967及2014年最大日径流数据。

5 结 论

本文选取汉江上游具有代表性的武侯镇、洋县、安康3个水文测站，分别对各站年径流量序列、区间汇水及年最大日径流量序列进行趋势演变及非一致性检验分析，并根据年最大日径流量非一致性检验结果进行水文非一致性频率分析，所得结论如下：

(1)3站年平均径流量均呈下降趋势，递减速率自上游向下游逐渐递增；3站均有突变发生，上游突变时间略早于下游。

(2)武侯镇-洋县及洋县-安康两段区间汇水水量均占下游测站水量的50%以上，是控制下游测站水量及突变的主要因素；区间汇水均存在突变，发生时间略早于下游测站，下游测站受区间汇水的影响具有一定的滞后性。

(3)武侯镇站年最大日径流序列呈微弱增加趋势，洋县站及安康站呈递减趋势，且安康站的递减趋势显著(通过0.05显著水平检验)；综合两种非一致性检验方法所得结果，武侯镇站及洋县站的拟合度较高，突变年份均为1991年；安康站的两种检验结果存在10 a的偏差期，拟合度较低。

(4)经一致性修正计算后，武侯镇站对应近期气候及下垫面条件下修正后100年一遇洪水设计值大于历史修正值；洋县站及安康站的修正结果与武侯镇站相反，对应近期气候及下垫面条件修正后100年一遇洪水设计值大于历史修正值，所得结果均符合各站年最大日径流的变化趋势。

(5)本文对汉江上游武侯镇、洋县及安康3站日径流量序列趋势及非一致性分析，得到受气候变化及人类活动影响的汉江上游年径流量呈逐年递减趋势，百年一遇洪水要求达到的设计值相应降低，若不考虑一致性修正问题，其结果可能是加大下游防汛安全工程的投资成本。