双关节机械手轨迹跟踪控制方法研究

北京信息科技大学自动化学院，北京 100192

一、引言

双关节机械手主要由两个关节共同操作，通过抓取、移动物体来完成指定的各项工作。双关节机械手可靠性高、灵活性强、运行速度快、处理能力强，极大地提高劳动生产率。因此，将模糊理论、鲁棒控制与RBF神经网络相结合，结合神经网络鲁棒控制方法，提出基于模糊神经网络的双关节机械手鲁棒控制方法，具体是利用鲁棒控制消除系统不确定性的影响，并通过PD控制来实现轨迹的跟踪与控制，鲁棒控制器的不确定上界由RBF神经网络的万能逼近特点来逼近，在鲁棒控制器的不确定性上界附近，模糊逻辑控制实现了鲁棒控制器有界层宽度的自动调整，实现了双关节机械手高精度轨迹跟踪控制，具有重要的理论意义和实际价值。

二、动力学模型

拉格朗日函数L均可定义为其总的动能K与总的势能P之差，即：

其中，K—系统动能；

P—总势能；

T—作用于系统的广义力向量，T=[t1t2……tn]T∈Rn。

一般可以采用两种方法对刚性机械手数学模型进行构建：

1、n自由度刚性连杆机械手系统动力学模型

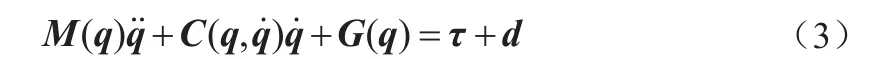
其中，q—双关节机械手关节的位置矢量；

—双关节机械手关节的速度矢量；

˙—双关节机械手关节的加速度矢量；

M(q) —n×n阶对称正定的惯量矩阵；

C(˙) —n×n阶离心力和哥氏力矩阵；

G(q) —n×1 阶重力矢量；

τ—关节的控制矩阵；

d—位置的外部干扰和建模动态向量。

2、n自由度旋转关节刚性机械手系统动力学模型

其中，Fd—n×n对角动态摩擦力矩阵；

Fs() —n×1阶的静态摩擦力向量。

三、基于模糊神经网络的鲁棒控制

1、问题描述

假设已经熟知机械手模型的相关知识，在无外界因素干扰的情况下，设计控制力矩为：

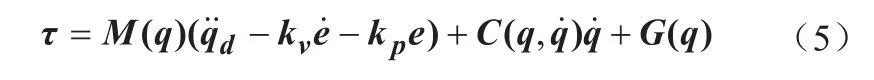
其中，e—位置跟踪误差，e=q-qd；

—速度跟踪误差，

kv—微分控制器增益矩阵；

kp—微分控制器增益比例。

将式（5）代入到（3），推导得出：

可以发现，公式（6）中，当对增益矩阵kv和kp进行合理的选择控制时，能够使跟踪误差渐近收敛到0。计算转矩控制器就是对控制器进行设计。

在式（5）中，如果kp和kv为正定对称的常数矩阵，那么就能够轻易的证明系统具有全局渐近稳定性。在已经熟知机械手模型相关知识的情况下，计算转矩控制具有适用性。对于双关节机械手系统，M(q)、和G(q)这一类参数矩阵可以分为标称模型参数矩阵和模型误差矩阵。其中，标称模型参数矩阵是模型误差矩阵为G(q)，表示参数的不确定性。各部分满足如下关系：

在实践应用中，由于外在环境的影响，各种干扰将不可避免。针对这种情况，对控制器进行设计：

由式（3）、式（7）到式（10）可推出系统的误差动态方程：

其中，Δf—由于不确定参数而引起的建模误差；

Δu—系统的建模误差以及外部扰动的误差；

u—非线性鲁棒补偿器，主要是用来增强系统对外部干扰的鲁棒性。

2、模糊神经网络鲁棒控制器设计

考虑摩擦以及外部扰动时的n自由度刚性机械手的动力学模型：

其中，M(q) —机械手关节的质量；

C(˙) —机械手臂杆长度；

G(q) —机械手关节惯量；

τ—关节的控制矩阵；

d—位置的建模动态向量和外部干扰；

Fd—摩擦项。

当不考虑外部环境干扰以及系统的不确定性因素时，设计控制力矩为：

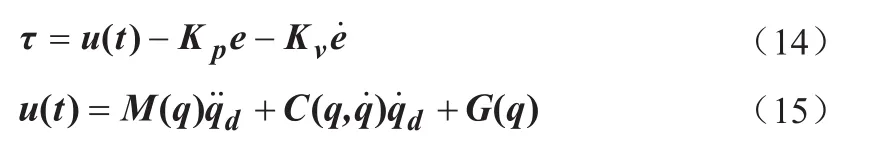
其中，q—双关节机械手期望轨迹的关节位置矢量；

—双关节机械手期望轨迹的关节速度矢量；

˙—双关节机械手期望轨迹的关节加速度矢量；

e—位置跟踪误差，e=q-qd；

—速度跟踪误差，

Kv—微分控制器增益矩阵；

Kp—微分控制器增益比例。

将式（14）和式（15）代入式（13）中，经过几步直接运算后可得如下的误差方程：

如前文动力学模型中所述，难以确定实际双关节机械手的不确定上界，并且一般保守估计方法将降低控制系统的精度。鲁棒控制器的不确定上界由RBF神经网络的万能逼近特点来逼近，在鲁棒控制器的不确定性上界附近。因此，借助RBF神经网络的射仪特征来分析补偿控制器（17）的不确定上界即：

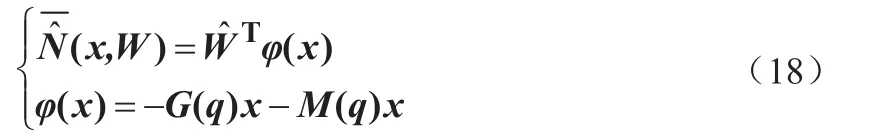
其中，G(q) —机械手关节惯量 ；

M(q) —机械手关节的质量；

—神经网络权值向量。

则基于神经网络的鲁棒补偿控制器为：

其中，η—自适应率。

采用max-min方法推导模糊控制器，采用加权平均判断方法解决模糊化问题。基于模糊神经网络的鲁棒补偿控制器可表示为：

其中，h—有界层的宽度。

四、仿真分析

1、机械手模型建立

采用S函数构建双关节机械手模型，为双关节机械手轨迹跟踪控制奠定基础。S函数程序步骤如下：

（1）初始化函数（flag=0）

确定双关节机械手的连续状态变量为q1、q2、在程序中参数用NumConStates=4表示，离散状态变量在程序中为0。双关节机械手输入的变量设置主要以涉及到的算法为依据，算法不同，输入的变量及个数也明显不同。根据本文的算法设计，双关节机械手的输出变量分别是两个关节的位置和速度。

（2）根据双关节机械手系统内部的相互关系，可以得到状态变量（flag=1），反映在程序中则是sys=mdlDerivatives(t, x, u)环节，具体为：

其中，x(2)、x(4)分别代表两个关节的速度；inv(M)*(tol'-C*dq-G-told)代表两个关节的加速度。

（3）计算系统的输出（flag=3）

机械臂的两关节位置和速度为系统的输出，状态变量x(1)、x(2)、x(3)和x(4)是其在程序中的具体表现。

2、参数设置

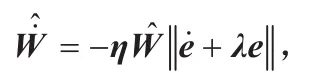
3、仿真结果分析

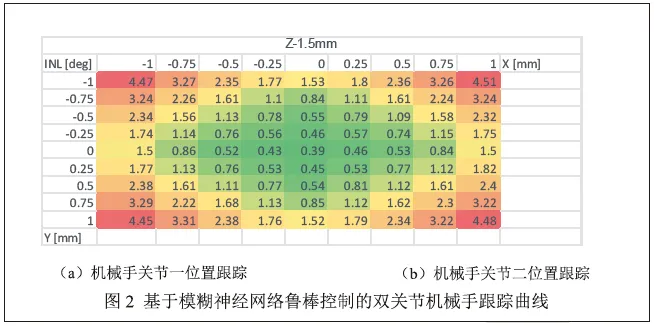
双关节机械手轨迹跟踪控制中，模糊神经网络鲁棒控制器作用下的关节1和关节2的位置跟踪曲线见图2所示。其中，期望运动轨迹用红色线条标记，实际跟踪轨迹用蓝色标注。

为了对基于模糊神经网络鲁棒控制器的效果进行分析，针对具有摩擦力和外部干扰等因素影响的双关节机械手仅采用PD控制进行跟踪效果仿真，具体结果见图3所示。

进一步采用模糊神经网络鲁棒控制器的两关节控制对双关节机械手的两个关节进行输入，具体结果见图4所示。

通过图2和图4的仿真结果可以看出，基于模糊神经网络的鲁棒控制器具有更好的跟踪性能和抗干扰性能，能够实现双关节机械手高精度跟踪，特别是对于关节2来说，跟踪性能更加显著。

结合图3和图4的仿真结果可知，相比于单个的PD控制器，基于模糊神经网络鲁棒控制器跟踪性能更好，误差较小，特别是关节2的跟踪性能尤其显著。基于模糊神经网络的鲁棒控制方法不需要事先知道机械手不确定性的上界，也不需要对惯性矩阵进行逆运算，这是它的最大优点，也是双关节机械手实现高精度轨迹跟踪的关键。

五、结论

文章以双关节机械手为例，结合机械手的应用优势和存在的不足，将各种不确定因素对系统的影响加以考虑，提出了基于模糊神经网络鲁棒控制方法。具体是将RBF神经网络引入到鲁棒控制中以补偿建模误差和外部干扰。RBF神经网络对鲁棒控制器不确定性的上界进行研究和逼近，模糊逻辑控制用于自动调整鲁棒控制器的有界层宽度。仿真结果表明，基于模糊神经网络的鲁棒控制方法可以帮助双关节机械手实现高精度的轨迹跟踪，验证了基于模糊神经网络鲁棒控制算法具有很好的跟踪性能，具有重要的理论意义和现实价值。