Space Debris Tracking Strategy through Monte-Carlo Based Track-before-Detect Framework*
Peerapong Torteeka, Gao Pengqi, Shen Ming, Guo Xiaozhong,Yang Datao, Yu Huanhuan, Zhou Weiping, Zhao You
(1.National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China, Email: youzhao@nao.cas.cn;2.University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract:The growing number of miniaturized satellites or small-body space debris is a challenging problem for autonomous ground-based space object observation.Although most space objects larger than 10 cm in diameter have been catalogued by North American Aerospace Defense Command,the precise orbital information of each space object(based on six orbital parameters)remains important and should be maintained periodically due to orbital perturbations.In the past decades,modern ground-based Electro-optic telescopes equipped with electronic detectors have been widely used in astrometry engineering.The tracking performance of this equipment primarily depends on the size and brightness of the space target.Moreover,in the real-time observation procedure based on STARE tracking mode in a short exposure time,the space object and stellar background will similarly appear in the point-spread function with different levels of signal-to-noise ratio under the variable conditions of background interference,which is difficult to recognize.The aim of present work is to achieve high-sensitivity detection and improved tracking ability for non-Gaussian and dynamic backgrounds with a simple mechanism and computational efficiency.To overcome this limitation,we emphasize robust tracking of small size satellite and faint object via a state estimation technique.We proposed a neural-network based adaptive running Gaussian average algorithm to extract a moving space object from the stellar background and its interference.The algorithm was integrated to a Track-before-Detect(TBD)framework which used Monte-Carlo based particle filter.The integrated algorithms were adopted to track the space object.Three sequential astronomical image datasets taken by the Asia-Pacific Ground-Based Optical Space Object Observation System(APOSOS)telescopes under different conditions were used to evaluate the tracking strategy.The results showed that the scheme achieved a satisfying tracking performance.
Key words: Space debris; Running Gaussian average; Neural-networks; Track-before-Detect framework
1 Introduction
To eventually perform low-cost space collision avoidance maneuvers,space debris localization which observed by ground-based space surveillance network remained the most powerful system over the last decade,especially from the Electro-Optic(EO)telescopes illustrated by a 3.5m DARPA telescope and 1.0m Lockheed Martin SPOT telescope[1-2].However,all of long-range EO astrometry are not robust under variable illumination conditions.Moreover,the high-altitude space debrisand small fragments are stealth appear on the screen normally, so it is difficult to detect automatically.Thus, the obtained measurement information could have been seriously missed, which makes the conventional tracking techniques inefficient.In this article, we propose a robust small and faint space debris detection and tracking strategy that is an integrated system between an intelligent object extractions and Monte-Carlo based Track-before-Detect framework(TBD).In both space and military missions, which have emphasized capabilities of tracking faint targets, the TBD frameworks all work with variable degree of success[3-4].The primary advantage of TBD is not needed to store and process multiple scans of data but it only requires hypotheses for extended target tracks and then updates using the measurement detection without a threshold value.Technically, in long-range observation, the kinematic model of the target can be described by the linear-stochastic process,which probably includes the target amplitude.However, the primary problem of TBD is the measurement model, which depends on the type of sensors.It is a highly non-linear function of the target state and directly influences the target position.Several TBD frameworks have been developed recently,such as dynamic programming and the polar-Hough transform[5-6].However, in real EO-based observations, the background noise frequently appears in dynamic and/or non-Gaussian backgrounds besides, over a short period of time, moving space debris and fixed-stars have a similar appearance in the pattern of the point-spread function(PSF)that requires the moving object extraction algorithms.Traditionally,the median image subtraction was applied in astrometry[7]with a first detailed description based on static and/or Gaussian backgrounds.As the extraction results,they used the rationale of pixels,which is the difference between the current frame and a reference frame called the background model.
To overcome this limitation,we propose a method that combines moving object extraction based on a running Gaussian average(RGA)adapted by the neural-network algorithm(RGA-NN)and TBD framework.We automatically optimize the dynamics of the astronomical background model under the condition of the NN algorithm.It is correlated with the simulation result of the previous work[8].The advantage of our proposed strategy is not only suppression of the background interference and low computation resources but also without the lack of burden or human bias.The remainder of this work is organized as follows.Section.2 discusses some background aspects of RGA-NN that are used to develop the robust extraction and TBD framework for real-time observations.Section.3 presents the specifications of the APOSOS telescope,the astronomical image datasets for validation, and some experimental results.Finally, Section.4 concludes this article.
2 Methodology
Technical speaking, the RGA is one of the computer vision technique, it is the updated version of static background subtraction,and has been widely used in the initial stages of moving object detection and tracking.However, in real environments, static background subtraction does not perform well on dynamic backgrounds.The basic RGA process can be expressed as follows:

where N is the number of frames used to construct the astronomical background(δ(Nx,y))in two-dimensional spatial coordinates(x, y), and I(kx,y)is the intensity of the present image ordered by k∈R+.After δ(Nx,y)has been constructed, we can calculate the absolute difference image(D(tx,y))between δ(tx,y)and I(tx,y)at time(t).We modify the new optimal δ(tx,y)using the empirical weight(α)∈[0, 1], which depends on the scene variability.In traditional RGA, the intensity level of D(tx,y)can be described by three cases based on twoboundary thresholds, the upper limit(τup)and lower limit(τlw).This can be written as follows:

Typically, α is manually adjusted according to human visual interpretation; it can be observed from the scene variability.This process is complicated,and readjustments are time-intensive.To overcome this limitation,a supervised feed-forward perceptron structure NN algorithm.The main structure of this algorithm comes from two important small components,which are neurons and activation transfer functions.They are inter-connected with other elements and become a complex networks,which is similar to the nervous system of the human brain.The fundamental functions of neural networks as follows:

where η is a neuron, the input vector is xi=[x1, x2, ..., xκ]′and W, b are the connecting weight matrix and bias vector between neurons, respectively.In Eq.(3)a is the activation state and f(η)is the activation transfer function.
The aim of this adaptive algorithm was designed to automatically adjust α based on Eq.(2)with two input parameters: the intensity level of D(x,y)tand the input image signal-to-clutter ratio(SCRi).Normally,the image SCR value represents the performance of small-target extraction, which can be defined as:

where μobis the average intensity of the object of interest, μbkis the average of the background intensity, andis the standard deviation(STD)of background intensity within the specified region of interest(ROI),which excludes the object region.For the training dataset of the NN algorithm, 200 points, which were symmetrically extracted,randomly based on the probability density function(pdf)and pre-identified by fourclasses,namely: large,normal, small and zero which symbolized as A,B,C, and D,respectively, as shown in Fig.1(a).To reduce the learning process time,the training dataset should be scaled in the optimal range[0,1]both horizontal and vertical axis as shown in Fig.1(b).We combined the proposed RGA-NN within the tracking loop to improve the measurement data.In the case of tracking single faint space target,TBD framework is a non-linear state-estimation methods based on the sequential Monte Carlo approximation that incorporates the prediction and updating stage, especially, to solve the hybrid state-estimation problems through the Particle Filter(PF)mechanism[9],where the state vector consist of two conditions that are continuous parts and discrete-value parts(presence of target or absence of target).However,conventional PF considers only one condition, which is the continuous appearance of the target in time; this condition is extracted by thresholding the output of the signal-processing unit of a sensor.In the prediction stage,the kinematic model of moving space debris on the celestial sphere projected to a spatial coordinate can be defined by the state vector xt=[px, vx, py, vy, Ω]′, where(px, py)t, (vx, vy)t, and Ωtare the position, velocity,and intensity level of the space debris,respectively.The propagation of state variables occurs according to a linear state transition matrix(At),which is a time invariant system with sampling interval(T).This can be defined in terms of the state vector using the linear stochastic equation:

Hence,

where wtis white Gaussian process noise with mean zero and covariance matrix Qt.The variances of the target acceleration and return intensity noise are represented in φ1and φ2, respectively.The two situations of the target(Et)consist of existence(e)and non-existence,which are described by the two-state Markov chain in the discrete-time domain[10].

Fig.1 The RGA-NN training dataset, which has 200 points randomly generated by the pdf(a)and the vector to be classified(b)
In theory,the two-state Markov chain model is a stochastic process for which the probability of entering a certain state(t)depends only on the last occupied state(t-1)and not on any earlier state.This is performed by a regime transition(RT)process,which transfers the state sequence through a square matrix named transition probability matrix(Π)having all entries non-negative and all column sums equal to 1.Furthermore,Π can be expressed as follows:,whereis the probability of target birth.The probability of target death is.The measurement model(z(ti,j))for moving space debris at each time interval consists of two conditions, which can be expressed as:

where h(ti,j)(xt)is the distribution intensity of space debris in each set of observation cells Oi(xt)and Oj(xt), as indexed by i, j, and ytis the measurement noise in each cell.We assume that ytis independent of wtand has a white Gaussian distribution with zero mean and variance ε2.In this study, the distribution intensity of space debris can be modeled by the PSF as a point target intensity at the rectangular position(px,py).Therefore, h(ti,j)(xt)as follows:

where Δxand Δyare the sizes of Oi(xt)and Oj(xt)in spatial coordinates.The variable ∑ represents the blurring coefficient of the PSF.The likelihood functions of the target in the two situations,which are the probability density function(pdf)of the background noise for each pthe pdf of the target existence in noise, consider the target state xt, Therefore, the two pdfs can be expressed as follows:
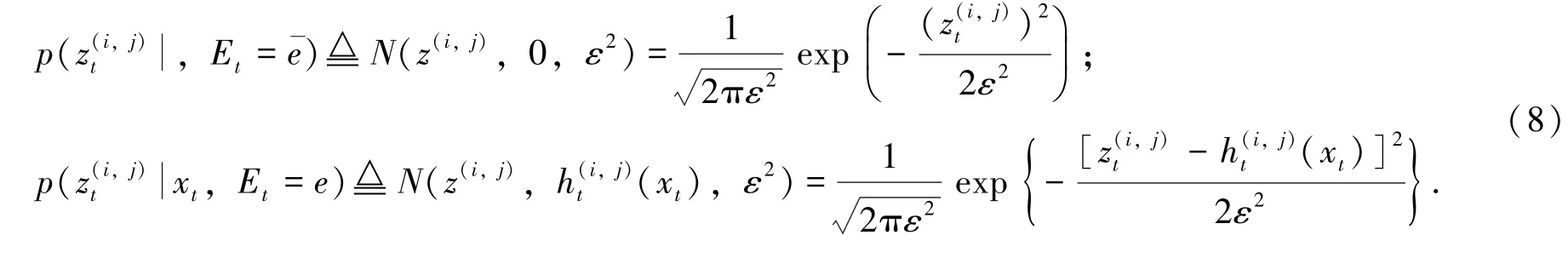
The case of target existence,will affect only the set of pixels around the target position(px, py), and the expression of this case can be estimated as follows:

Thus, the likelihood ratio for each cell is defined as follows:

From Eq.(10), the likelihood function of the target existence is given as:

The variables nland ncare the number of pixels in the observation cells,which are affected by the space debris intensity.
3 Specification of APOSOS telescope and image datasets
In our experiment,we used input images from three datasets of a real astronomical background obtained by an azimuthal-mounted APOSOS telescope[11]equipped with a complementary metal-oxide semiconductor(CMOS)-type high-resolution sensor.These were stored as flexible image transport System(FITS)-type grayscale images with range[0,255],150-mm aperture size,300-mm focal length,and a 3×3 degree2FoV.In detail,the specification are listed in Table 1.The observation site(WGS84)was located at National Astronomical Observatories, CAS, Beijing, China(Lat.43.845 00 and Long.125.400 80 degrees).For the telescope guidance system,the APOSOS telescope applied the orbit parameters of two line elements to calculate the orbital prediction,which was provided by North American Aerospace Defense Command.The datasets cover the three primary situations in space observation with exposure time: ≈50 ms; (i)normal-sky tracking of 32 frames, (ii)a small and faint space-object tracking of 25 frames, and(iii)a critically dynamic background tracking of 25 frames.These were labelled as datasets A, B, and C, respectively, as shown in Fig.2.

Table 1 The specification of APOSOS telescope

Fig.2 (a)-(c)are the tracking datasets of space object named A,B,and C, with known orbital parameters,respectively.The red rectangle marks are the observations with a 64×64 pixels2 ROI around the space object
4 Experimental results and discussion
The background clutter is typically non-Gaussian and independent,both pixel to pixel and frame to frame, which can be observed from σROIbk, as shown in the bottom of Fig.3(d), (e), and(f).Moreover, this parameter is inversely proportional to the extraction performance.In this experiment,the traditional object extraction technique named median image subtraction[12]was used to compare the background suppression factors with the proposed RGA-NN method over three benchmarks of real astronomical images sequences under the three primary interference conditions in observation time.Normally,the energy of long-distance imaging target is very weak; therefore, the target account for only one or a few pixels in the astronomical screen, which are the cause of the low-dynamic range as shown in red rectangle marks of Figs.2(a)-(c).The first experiment is related to the moving object-extraction procedure; Fig.3(e)shows the NN-α (top)and σRbkOIof dataset B, which is relatively stable or clear-sky background.As a result, the NN-α is consequently inserted in based on the conditions of Eq.(2).

Fig.3 (a)-(c)are the comparison of the extraction performance with datasets A,B,and C,respectively,and(d)-(f)are the average of NN-α based on the second condition of Eq.(2)and STD in a specific ROI corresponding to dataset A, B,and C,respectively
Otherwise,in datasets A and C,as shown in Figs.2(a)-(c),both normal and critical dynamics of the atmospheric effect causing NN-α consequently insert in I(tx,y).Fig.3(a)-(c)depict the comparison of the extraction algorithms indicated by the output SCR.From the Fig.3(a)-(c)it is clearly proved that the proposed RGA-NN approach outperforms the median technique under the three categories of background interference, especially, the condition of a dynamic background.As the results, the average output SCR of the median and RGA-NN approaches are 5.245 and 6.324 for dataset A,9.991 and 11.130 for dataset B,and dataset C at 7.105 and 7.863, respectively.For the extraction performance, factors consist of improved-SCR(iSCR),which represents the enhancement of the extraction procedure with SCRibefore and after processing with output SCR and the background suppression factor(BSF),as illustrated in Table 2.

Table 2 Comparison of space-target extraction algorithms
To evaluate the tracking performance,the kinematic of moving space targets in spatial coordinates was designed based on the dead-reckoning approach.We assumed that the single moving space-debris object appeared to cover the whole image sequence with a constant velocity and crossed over the critically dynamic background area, typically Figs.2(c-2)-(c-4)show dataset C.For the star image registration, we usedthe USNO-B 1.0 star catalog to identify fixed stars for reference positions and transformed the estimated position in 2D spatial coordinates to celestial coordinates based on the least-squares method.Then,the reference fixed stars were recognized by δ(Nx,y).The tracking performance with the proposed method was evaluated in terms of accuracy and robustness in a comparison with the two types of combination algorithms:median-TBD and RGANN TBD.Although the tracking accuracy improved with the number of particle size,the computation time also linearly increased.In the detection and tracking process, first, the TBD framework operated with the optimal number of particles: np≈750; the processing time around 40 ms in average.The particle uniform proposal densities were set as xp(tx,y)~ρ(-5, 5), xv(tx,y)~ρ(-3, 3), and xτt~ρ(-5, 5), with the probability of target existence at Pb=Pd=0.01.Tracking with the observation size was Δx=Δy=5.The tracking accuracy could be computed as the root mean square error(RMSE).In the first tracking experiment,we employed both datasets A and B, which are a common scenario in low-clutter background and faint space target conditions,respectively.For dataset A,it included a partly Gaussian interference background with a different variance in the last fifteen frames,as illustrated by the STD clutter level in Fig.3(d).The tracking performance using both datasets is shown in Figs.4(a)-(b).In a comparison,using the average RMSE value considering only the present frames for both datasets,the median-TBD and RGA-NN TBD are 0.120 0 deg.and 0.052 2 deg.and are 0.307 6 deg.and 0.033 2 deg.for datasets A and B., respectively.In the second experiment, we emphasized on dataset C.As shown in Fig.3(f),the fit data(red dashed line)has an increasing trend and change of the STD clutter level.The object path is shown in Fig.4(c).It is evident that the non-Gaussian interference has an effect in terms of position accuracy,the static background model of the median technique can approximate the position and orientation of the space target; however, from that point, the SCR declines due to the clutter signal,which causes the velocity bias of both directions in median-TBD to be increasing continuously.Nevertheless, in the case of RGA-NN TBD, tracking continues under this condition with an average RMSE of 0.149 7 deg.Note that,we did not adjust the TBD parameters in the new environment in order to determine the robustness.

Fig.4 (a)-(c)are estimation of positions of datasets A,B,and C given by two methods and(d)-(f)are the probabilities of existence(bottom)and position-based RMSE(top)corresponding to datasets A,B,and C,respectively
5 Conclusion
In summary,we presented techniques to solve the problem of the tracking strategy of small and faint space targets for the EO-based telescope.The proposed methods combined two main steps.The first stage is the extraction approach in which we apply the artificial NN and automatically estimate the optimal value of the empirical weight in traditional RGA.The learning process of NN was designed using two primary parameters,which are input SCR of the present image and absolute difference in stochastic RGA process.According to the results, this approach not only reduces the effect of a dynamic background, but it also improves the extraction performance and robustness more than the traditional median technique as shown in Table 2.the iSCR of Dataset A,B,and C via RGA-NN are improved with 23.2%,9.6%and 11.3%,respectively.We then integrate the first procedure with the second stage,a TBD approach.The results demonstrate that the proposed combination algorithms provide considerable improvement in tracking accuracy, precision, and robustness compared to other methods when the level of real background noise covariance is changed.
Acknowledgements:The authors are thankful for the support from The World Academy of Sciences(TWAS),the Chinese Academy of Sciences(CAS),and Asia-Pacific Space Cooperation Organization(APSCO).

